自行式高空作业平台的动态稳定性分析

高旭宏，徐向阳，王书翰，王增全



自行式高空作业平台的动态稳定性分析

高旭宏1, 2，徐向阳1，王书翰1，王增全2

(1. 北京航空航天大学交通科学与工程学院，北京，100191；2. 北京航天发射技术研究所，北京，100076)

为了分析自行式高空作业平台作业过程中的动态稳定性，以数学模型为基础，采用ADAMS软件建立整车的动力学仿真模型，对6种最危险的作业工况进行仿真计算，得到不同工况下各轮胎承载的载荷特性曲线及整车动态稳定性的安全系数。最后，进行场地试验测试。研究结果表明：测试数据与仿真计算数值间的极值相对误差最大为13.4%，试验测得动态稳定性的最小安全系数为0.123，验证了整车在作业过程中具有良好的动态稳定性，也验证了对自行式高空作业平台使用动力学仿真和试验测试相结合的分析方法的正确性和准确性。

自行式高空作业平台；动态稳定性；安全系数；ADAMS软件

自行式高空作业平台作为一种新型高效的工程机械，具有自行走能力，广泛应用于船舶、航天、建筑、租赁等行业。美国、欧洲、日本等发达国家对自行式高空作业平台的研制始于20世纪六七十年代，研发技术处于领先地位。国内对自行式高空作业平台的研制较晚，2000年至今，生产企业约20家[1−2]。自行式高空作业平台是承载人员高空作业的设备，工作中最重要的性能是整车的稳定性。目前，欧洲现行使用的标准EN 280:2010和我国颁布的标准GB 25849—2010以及GB/T 9465—2008都有明确的规定：“在制造商允许的使用情况下，整车的支撑必须具有良好的稳定性，不发生倾覆”[3−5]。对自行式高空作业平台等高空承载类设备作业过程中动态稳定性的分析，国内外科研人员进行了大量研究。其中，PANA等[6]从倾覆事故统计数据的角度分析了不同类型高空作业平台稳定性的特点。ROSS等[7]以某大型起重设备倾覆事故为基础，重点分析了臂架结构和风载荷等因素对高空作业设备稳定性的影响。TOWAREK等[8]基于不同的路面条件，对高空作业设备处于不同承载状态时的稳定性进行了分析。CASTILLO等[9]借助微积分算法，对土木工程中使用的起重类高空作业设备，进行了斜坡作业条件下的稳定性分析。GHIGLIAZZA等[10]对起重机等高空作业设备，提出了设置回转加速度最优限值的方法以提高作业过程中的动态稳定性。RUZZENE等[11]分析了随车起重机承载后的临界运动速度对其动态稳定性的影响。MIKKOLA等[12]从检测高空作业设备疲劳损坏的角度出发，研究了超载疲劳与动态稳定性间的关系。赵洪亮[13]采用力矩法建立了蜘蛛式高空作业平台的数学模型，并利用MATLAB求解得到了抗倾覆稳定性系数；赵静一等[14]通过平衡法建立数学模型来求解最小的轮胎支反力，进而确定高空作业平台的作业范围；陈国安等[15]对高空作业设备提出求解支腿最大支反力可能值的计算方法，得到了整机最低的稳定作业状态；李建涛等[16]提出利用主客观6个评价指标反映四支撑装置作业稳定性的分析方法。TONG等[17]对港口使用的起重设备建造了一个1:5的试验模型，通过试验模型测试与仿真计算间不断地比较，来分析作业过程中的动态稳定性。从以上国内外的研究成果可以看出，自行式高空作业平台在作业过程中的动态稳定性与地面坡度、臂架状态、轮胎承载、回转速度等多因素相关。但现有对自行式高空作业平台作业过程中动态稳定性的研究，尚未发现采用建立整车的动力学仿真模型，并使用仿真计算与试验测试相结合的分析方法。因此，本文作者依据某自行式高空作业平台的结构特点和作业方式，以数学分析模型为基础，采用ADAMS软件对其建立了动力学仿真模型，对6种最危险的作业工况进行计算，得到各轮胎承载载荷的动态特性曲线和动态稳定性的安全系数。接下来对实物进行场地试验测试，通过对比分析试验结果和计算结果，验证分析方法的正确性和准确性。

1 数学分析模型

自行式高空作业平台主要由底盘、转台、臂架、油缸、支座、工作平台等部件组成，作业过程中的倾覆状态分为倾翻和仰翻，其受力关系如图1所示。

当整车处于倾翻或仰翻状态，稳定力矩的计算方法如下[18]。

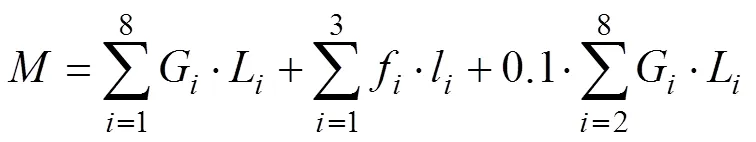
式中：G为底盘、转台、臂架等各部件的重力；L为底盘、转台、臂架等各部件对倾覆线的水平距离；1和2为风载荷，3为手操作力；l为风载荷和手操作力对倾覆线的垂直距离；运动部件的动态载荷系数取0.1[3−4]。

若式(1)中的稳定力矩为零或负数，说明整车处于倾覆临界状态或已发生倾覆。但为正数时也不能过小，所以还要计算轮胎的最小支反力及动态稳定性的安全系数，计算方法如下。

(a) 倾翻状态；(b) 仰翻状态

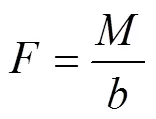
式中：为相对于倾覆线某侧2个轮胎的最小支反力之和；为某侧2个轮胎支反力作用点对倾覆线的垂直距离。

式中：为动态稳定性的安全系数。

当转台以上的运动部件在0°~360°回转过程中，整车处于最不利的稳定条件(即臂架回转至90°或270°位置)，安全系数即为可能发生倾覆危险一侧的前后2个轮胎承载力之和与整车总质量的比值。安全系数的数值结果越小，说明整车在作业过程中的动态稳定性越差，但目前对安全系数的最小值并没有明确的规定，而自行式高空作业平台可以参考GB 3811—2008起重机设计规范中的规定：“在额定承载的任意工况下，支腿或车轮上的总载荷不小于起重机总重的10%”[19]。

2 建模及仿真

2.1 建立模型

首先，在UG中建立整车的三维模型，包括底盘、转台、油缸、轮胎、支座、工作平台等。同时，在ANSYS中建立臂架的弹性体有限元模型。随后，将各模型依次导入ADAMS软件中进行装配，如图2所示。

在ADAMS/Tire的模块下设定轮胎为Fiala模型，臂架是在ANSYS中建立的弹性体有限元模型，两者都属于柔性体，其他部件均简化为刚性体。设置底盘的回转中心点为坐标原点，轴为底盘的纵轴线，轴垂直地面，轴按右旋法则确定。接下来依次对各连接部位设置转动副、移动副等运动关系，对臂架、转台和油缸设置驱动关系。

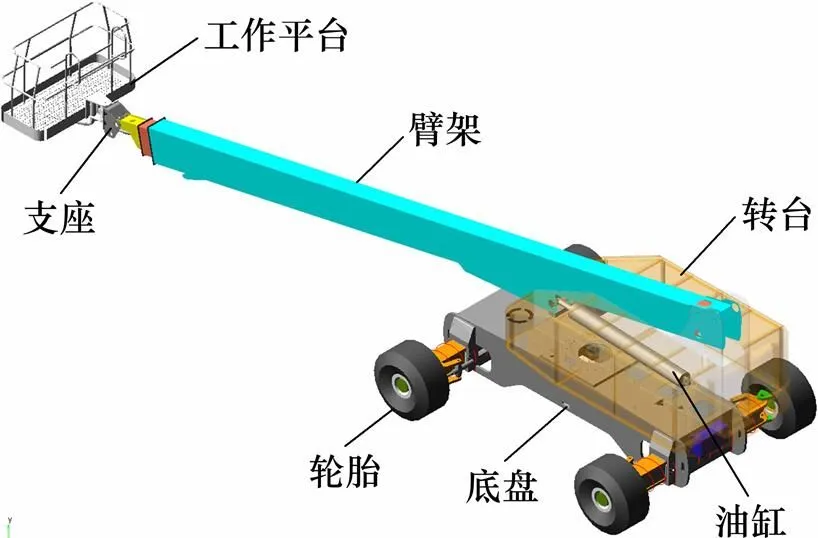
图2 自行式高空作业平台的动力学模型

2.2 确定仿真工况

按照标准EN 280和GB 25849中的要求，选择6种最危险的作业工况进行动态稳定性的分析，如表1所示。

由表1可见：工作允许的路面坡度为0°~5°，且5°选取底盘处于最危险的横坡工作状态。按照国内外技术标准的要求，将运动部件产生的动载荷、风载荷和手操作力等各种附加载荷使用加倍静载荷的方式进行放大替代[3−5]。所以额定承载是230 kg，在倾翻状态下取其1.5倍额载，载荷为345 kg，而在仰翻状态下取最不利的载荷80 kg(相当于仅1人)[3−5]。

按照表1中的要求，对工况进行了组合，路面设置为水平状态或将底盘左侧的2个轮胎同时垫高300 mm，即使车体产生5°的横向倾斜，当臂架举升和伸出到位后，按设计的最大回转速度匀速地进行0°~360°的连续回转，在ADAMS中的仿真过程如图3所示。

表1 危险作业工况

(a) 工况1和4；(b) 工况2和5；(c) 工况3和6

3 仿真结果及分析

通过仿真计算，得到不同工况下各轮胎承载的动态特性曲线，如图4(a)~(f)所示。

通过仿真计算，得到了6种作业工况下各轮胎承载的动态特性曲线，其中FL，FR，RL和RR分别代表左前轮、右前轮、左后轮和右后轮；线和线分别代表轮胎载荷的上下极值线，从图4可以看出：

1) 由图4轮胎承载的最小值线可知，未出现任何一个轮胎承载力为零的情况，说明整车动态稳定性好，理论上无倾覆风险(包括倾翻和仰翻)。

2) 从图4载荷曲线的变化规律上看，具有非常规则的对称性，说明建立的动力学分析模型比较准确，整车质心位于纵向对称平面内。

3) 在图4中，以FL(左前轮)为例，最小的承载力分别为32 505，35 677，8 867，28 067，28 364和4 821 N，图4(d)与(a)、图4(e)与(b)、图4(f)与图4(c)相比，轮胎的最小承载力分别下降了13.7%，20.5%和45.6%，说明在5°横坡工况作业时，整车的动态稳定性显著 下降。

4) 图4(f)中270°位置对应的FL(左前轮)和RL(左后轮)的轮胎承载力之和为最小值21 231 N，重力加速度取9.8 N/kg，所以通过仿真计算，理论上得到整车作业过程中最小的动态稳定性的安全系数为0.115 (即21 231/(18 800×9.8))。

4 试验测试及分析

4.1 场地试验

为检验仿真计算的准确性和整车实际作业过程中的动态稳定性，分别对某自行式高空作业平台进行了水平路面状态和5°横坡路面状态的场地试验测试。在测试过程中，使用4个量程为10 t的称重传感器(测量误差±5 kg)，分别布置在4个轮胎的正下方，并使用2块300 mm高的长方形枕木作为5°工况的支撑工装，垫在左侧前后2个轮胎和称重传感器之间。

鉴于试验测试方法的可操作性及测试数据与仿真计算数值间的可比较性，在倾翻测试中将运动部件产生的动载荷、风载荷和手操作力等各种附加载荷，使用加倍额定静载荷的方式放大替代[3−5]。所以，对于倾翻测试，在工作平台处施加载荷为345 kg (额定载荷230 kg的1.5倍)；而对于仰翻测试，工作平台处施加最小的载荷(80 kg)。

(a) 工况1；(b) 工况2；(c) 工况3；(d) 工况4；(e) 工况5；(f) 工况6

测试过程中，将控制回转功能的电比例液压阀的流量调至最大，使臂架能以最大的回转速度在0°~360°间连续地匀速回转，其中部分试验测试环节如图5和图6所示。

图5 工况2测试环节

图6 工况6测试环节

4.2 测试数据分析

试验测试过程中，运动部件(包括臂架、转台、油缸、工作平台等)在0°~360°间连续匀速回转，当臂架处于8个不同的位置(即0°，50°，90°，130°，180°，230°，270°，310°和360°)时，记录称量传感器显示的数值，分别对每个工况进行4次测试(顺时针和逆时针回转各2次)，对测试结果均值化处理后，再使用MATLAB软件拟合数据，从而得到了6种最危险的作业工况下各轮胎承载载荷的测试数据曲线，如图7 所示。

将场地试验的测试结果与仿真分析的计算结果进行了统计和比较，如表2所示。

表2 轮胎载荷极值的比较

通过图4与图7所示的轮胎承载曲线的对照，以及表2中轮胎载荷极值的比较和实测得到的动态稳定性的安全系数，可以看出：

1) 图7中轮胎承载的测试结果与图4的仿真分析结果相比较，轮胎承载曲线的变化趋势完全一致，说明对整车建立的仿真分析模型与实物的真实状态基本一致。

2) 试验测试得到的各工况下轮胎承载的极值，与对应状态的仿真计算结果相比较，最大相对误差为13.4%，最小相对误差为1.0%。从误差的分布规律上看，工况1和4产生的误差最大，工况3和6产生的误差次之，工况2和5产生的误差最小。产生这种误差分布的主要原因是仿真计算过程中将臂架设置为柔性体结构，而工况1和4是臂架挠度最大的工况，工况3和6是臂架挠度最小的工况，表明臂架采用柔性体模型的设计精度还需提高。但总体相对误差均不超过15%，说明仿真分析模型的计算结果能真实反映出整车实际的工作状态。

(a) 工况1；(b) 工况2；(c) 工况3；(d) 工况4；(e) 工况5；(f) 工况6

3) 通过分析图7(a)和(d)，起始位置时左侧两轮胎的承载力均明显比右侧的小。经对实物检查，是由于制造误差造成了臂架的第3节臂与第2节臂套接后，单侧间隙超差(设计要求的间隙是单侧各2.0 mm，而实际左侧为2.7 mm，右侧为1.3 mm)，进而造成了整车实际的质心偏向右侧。所以臂架水平伸出最远时，左侧轮胎产生的偏载也最严重。而从图7(b)与(e)、图7(c)与(f)可见：当臂架处于53°举升或完全缩回状态时，臂架单侧间隙超差对左侧轮胎偏载的影响已明显减小。因此，重点控制臂架的制造精度和装配后的侧面间隙尺寸，能有效保证整车作业过程中的动态稳 定性。

4) 在图7(f)中270°的回转位置时，FL(左前轮)和RL(左后轮)的轮胎承载力之和为23 232 N，达到整车稳定状态的最小承载值。经测量，试验时整车总质量是19 216 kg，重力加速度取9.8 N/kg，则测试得到整车最小的动态稳定性的安全系数为0.123(即23 232/ (19 216×9.8))。

5) 鉴于试验测试方法的可行性，本实验过程中采用了施加1.5倍额定载荷和最小载荷的测试方法，而在实际作业中按照额定载荷230 kg使用，不会发生1.5倍过载的情况(因工作平台处安装了1.2倍过载的保护限制)，也很少出现最小载荷80 kg的使用情况，所以，整车实际作业过程中的动态稳定性会更好。

5 结论

1) 通过仿真计算，得到了各轮胎承载载荷的特性曲线，确定了整车在作业过程中具有良好的动态稳定性，不会发生倾覆。

2) 通过场地试验测试，验证了实物车辆实际作业过程中的动态稳定性。通过测试数据与仿真结果的比较，轮胎承载极值的最大相对误差为13.4%，验证了采用动力学仿真分析方法的正确性和准确性。

3) 基于测试数据与仿真结果间的误差分析，确定了臂架套接安装后的侧面间隙尺寸是影响整车动态稳定性的一重要因素，装配过程中必须进行严格的工艺控制。

4) 从安全使用的角度考虑，出厂前应对整车进行1.5倍静载工况的测试，其动态稳定性的安全系数不应低于0.1。

[1] 王飞. 高空作业平台国内外市场发展概述[J]. 建筑机械化, 2009, 30(12): 34−36. WANG Fei. An overview of domestic and international aerial working platform market development[J]. Construction Mechanization, 2009, 30(12): 34−36.

[2] 张磊庆. 国内外高空作业平台市场展望[J]. 建筑机械化, 2012, 33(4): 42−43. ZHANG Leiqing. Market forecast of domestic and international aerial work platform[J]. Construction Mechanization, 2012, 33(4): 42−43.

[3] EN 280:2010, Mobile elevating work platforms-design calculation-stability criteria-construction-safety-examinations and tests[S].

[4] GB 25849—2010, 移动式升降工作平台设计计算、安全要求和测试方法[S]. GB 25849—2010, Mobile elevating work platforms: design calculations, safety requirements and test method[S].

[5] GB/T 9465—2008, 高空作业车[S]. GB/T 9465—2008, Vehicle-mounted mobile elevating work platform[S].

[6] PANA C S, HOSKINB A, MCCANNC M, et al. Aerial lift fall injuries: a surveillance and evaluation approach for targeting prevention activities[J]. Journal of Safety Research, 2007, 38(6): 617−625.

[7] ROSS B, MCDONALD B, VIJAY SARAF S E. Big blue goes down. The Miller Park crane accident[J]. Engineering Failure Analysis, 2007, 14(6): 942−961.

[8] TOWAREK Z. The dynamic stability of a crane standing on soil during the rotation of the boom[J]. International Journal of Mechanical Sciences, 1998, 40(6): 557−574.

[9] CASTILLOA E, MÍNGUEZ R, CASTILLO C. Sensitivity analysis in optimization and reliability problems[J]. Reliability Engineering & System Safety, 2008, 93(12): 1788−1800.

[10] GHIGLIAZZA R M, HOLMES P. On the dynamics of cranes, or spherical pendula with moving supports[J]. International Journal of Non-Linear Mechanics, 2002, 37(7): 1211−1221.

[11] RUZZENE M, BAZ A. Dynamic stability of periodic shells with moving loads[J]. Journal of Sound and Vibration, 2006, 296(4): 830−844.

[12] MIKKOLA A. Using the simulation model for identification of the fatigue parameters of hydraulically driven log crane[J]. Journal of Mechanical Design, 2001, 123(1): 125−131.

[13] 赵洪亮. 高空作业平台稳定性分析[D]. 西安: 长安大学工程机械学院, 2010: 25−35. ZHAO Hongliang. Stability analysis of the aerial working platform[D]. Xi’an: Chang’an University. School of Construction Machinery, 2010: 25−35.

[14] 赵静一, 苗增, 程斐, 等. 高空作业车支反力计算及作业半径规划[J]. 机床与液压, 2011, 39(16): 1−3. ZHAO Jingyi, MIAO Zeng, CHENG Fei, et al. Calculation of the support reaction and planning of working radius on aerial platform[J]. Machine Tool & Hydraulics, 2011, 39(16): 1−3.

[15] 陈国安, 朱真才, 李思鼎. 工程机械支腿最大受力值计算[J]. 中国工程机械学报, 2010, 8(2): 162−165. CHEN Guoan, ZHU Zhencai, LI Siding. Maximum loading calculation for construction machinery outriggers[J]. Chinese Journal of Construction Machinery, 2010, 8(2): 162−165.

[16] 李建涛，李继波. 四支撑装置稳定性研究及应用[J]. 重型机械, 2013(3): 47−51. LI Jiantao, LI Jibo. Stability research and application of four-supported device[J]. Heavy Machinery, 2013(3): 47−51.

[17] TONG Minhui, WANG Yuemin, QIU Huiqing. Dynamic responses of high speed quay container cranes[J]. Procedia Engineering, 2011, 16: 342−347.

[18] 张帆. 自行式高空作业车虚拟运动系统[D]. 大连:大连理工大学机械工程学院, 2008: 20−26. ZHANG Fan. A virtual motion system of aerial working platform[D]. Dalian: Dalian University of Technology. School of Mechanical Engineering, 2008: 20−26.

[19] GB 3811—2008, 起重机设计规范方法[S]. GB 3811—2008, Design rules for cranes[S].

(编辑 杨幼平)

Dynamic stability analysis of self-propelled aerial work platform

GAO Xuhong1, 2, XU Xiangyang1, WANG Shuhan1, WANG Zengquan2

(1. School of Transportation Science and Engineering, Beihang University, Beijing 100191, China;2. Beijing Institute of Space Launch Technology, Beijing 100076, China)

In order to calculate the dynamic stability of the self-propelled aerial work platform (SAWP) at work, the analysis method based on mathematical model and dynamic simulation model of the SAWP was put forward. Then the dynamic simulation model of the SAWP was made with software ADAMS. Six kinds of the most dangerous working conditions were analyzed, and then the dynamic load curves of tires and dynamic stability safety coefficient were obtained. At last, the dynamic stability of the SAWP was verified by the field experiment. The results show that the maximum error between test data and numerical simulation calculation is 13.4%, and the dynamic safety coefficient is 0.123. So the dynamic stability of the SAWP at work is satisfied. At the same time, combining dynamic simulation and test analysis method of the SAWP is proved in terms of correctness and accuracy.

self-propelled aerial work platform; dynamic stability; safe coefficient; ADAMS software

10.11817/j.issn.1672−7207.2017.10.038

TH213.6

A

1672−7207(2017)10−2836−07

2016−10−12；

修回日期：2017−02−01

国家自然科学基金资助项目(51105017)(Project (51105017) supported by the National Natural Science Foundation of China)

王书翰，博士，副教授；从事多学科系统动力学的建模与仿真研究；E-mail：wsh@buaa.edu.cn