基于全尺度线热源解的地热换热器集群的温度响应

李平，李旻，马卫武，肖莲荣



基于全尺度线热源解的地热换热器集群的温度响应

李平1，李旻1，马卫武1，肖莲荣2

(1. 中南大学能源科学与工程学院，湖南长沙，410083；2. 湖南亚华乳业有限公司，湖南长沙，410013)

针对地热换热器集群的跨尺度传热难题，运用匹配渐进展开法和叠加原理，构建全尺度线热源解。计算2种钻孔布置形式(单行和矩阵)的温度响应，分析钻孔间距对地下温度演化过程的影响。从工程应用的角度探讨简化计算地热换热器集群平均温度的问题。研究结果表明：所提出的全尺度线热源解扩展了国内外现有解析解的适用范围。

地源热泵；地埋管换热器；温度响应函数；全尺度模型

地埋管换热器传热是一个复杂的非稳态过程，涉及的时间长、空间大：从厘米级的埋管管径到上百米的换热器群的横纵向尺寸，共跨4个数量级，对应的时间尺度则跨8个数量级(数分钟到数十年)[1−2]。大规模地热换热器集群的传热分析(无论是实验还是理论研究)的主要问题是如何高效地求解这个时空尺度跨度大的难题。地热换热器的传热分析常将传热热阻以钻孔壁为界分为稳态与非稳态2部分。计算钻孔内稳态热阻的模型包括经验与理论模型2类。最典型的经验模型采用“当量直径”的概念[3]。经验公式简单易用[4−5]，但缺乏传热理论基础，不具有普适性。理论热阻模型包括二维模型和准三维模型[6−8]。常见的二维模型有基于稳态线热源解和multipole解2类。准三维模型能计算流体温度沿钻孔轴向的变化，是对二维模型的进一步修正[6−8]。钻孔外的非稳态热阻归结为对温度响应函数(函数)的计算。INGERSOLL等[9]提出的无限长圆柱模型与无限长线热源模型已被广泛采用和拓展[10−11]。例如，基于镜像法的有限长线热源模型能考虑钻孔端部效应[12−13]，适用于长时间的传热过程；运用移动热源法能够估算地下水渗流的影响[14−15]；基于NEUMANN方法，无限长线热源解被扩展并用于计算地下水凝固与融化的影响[9]；结合叠加原理还可以计算变负荷工况等[16−17]。这些传热模型存在明显局限性，即钻孔内的稳态传热假设不适合计算短时高频温度响应。高频温度响应受钻孔内介质的热容影响，与地源热泵的峰值温度、最优控制和逐时能耗分析等问题密切相关，是该领域的研究热点和难点[18−21]。其难点在于涉及复合介质和不规则几何形状。目前，国内外广泛采用的方法是数值解法和简化问题的几何形状。常用的简化仍是“当量直径”假设[18−21]。为了抛弃这个经验性假设，LI等[22−23]提出复合介质线热源模型，较好地解决了计算高频温度响应的难题。基于复合介质线热源解，进一步构建适用于所有重要时空范围的全尺度线热源模型[2]和对应的准三维模型[24]。但是，该模型只适用于单个地埋管换热器，不能考虑多个钻孔之间的影响。为此，本文作者进一步拓展全尺度线热源模型，使其能考虑钻孔间的影响，从而为地热换热器集群的设计和分析提供更可靠的参考依据。

1 全尺度线热源模型的拓展

全尺度线热源模型将地埋管换热器换热过程以U型管壁壁面为界分为2部分(见图1)：U型管壁面外(包括钻孔内回填材料部分)的非稳态传热过程和U型管内的准稳态传热过程。全尺度模型实际上综合了地埋管换热器的3个解，即适用于短时间的复合介质线热源解i，适用于长时间的有限长线热源解o和适用于中间时间的无限长线热源解m[2]：

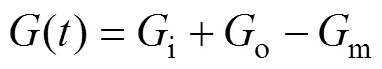
其中：为单位阶跃负荷下的温度响应函数，其量纲与热阻的相同。复合介质线热源解i的出发点是将U型管管脚(不是钻孔)近似为复合介质中的线热源[23]。简而言之，复合介质就是不同区域传热介质不同。因为地埋管换热器钻孔内外的介质不一样，所以，这是1个复合介质中的导热问题。i的推导过程见文献[23−24]。

(a) 单U埋管换热器；(b) 单U埋管的复合介质线热源近似；(c) 双U埋管换热器；(d) 双U埋管的复合介质线热源近似

图1 地热换热器的复合介质线热源假设示意图

Fig. 1 Assumption diagrams of composite-medium line-source for one and two U-shaped ground heat exchangers

对于单U型埋管：

对于双U型埋管：

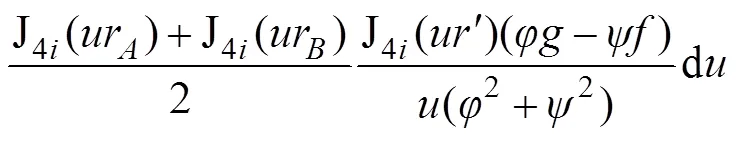
式中：为时间；b为回填土热传导系数，W/(m2∙℃)；b为回填土的热扩散系数；为线热源的径向位置；r和r分别为图1中和点的径向坐标；为积分变量；

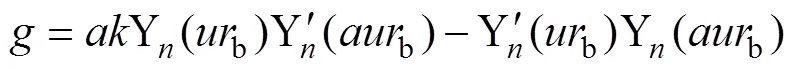
式中：b为钻孔半径；J和Y分别为第一类和第二类阶贝塞尔函数；在方程(2)和(3)中，分别为2和4，为式中求和的指标；为量纲一热扩散系数，= (b/s)1/2；s为土壤热扩散系数；为量纲一热传导率，=s/b；s为土壤热传导系数(W/(m2∙℃))。

o为适用于长时间的传统有限长线热源解，其表达式如下：

式中：′为沿轴的积分变量；为钻孔高度；erfc()为补余误差函数；m为适用于中间时间的无限长线热源解，

式中：为积分变量。

求得()后，U型管壁面温度可表示为

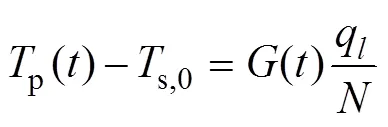
单位阶跃冷热负荷下循环水温度响应可用下式表示：

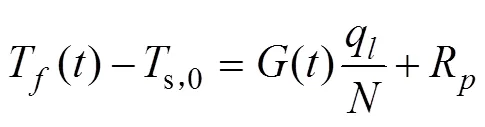
其中：s,0为地下土壤的初始温度；p为U型管的热阻，

p为U型管热传导率；为热对流系数；o和i分别为U型管管脚的外径和内径。对于单U型管地埋管排布形式，2；对于双U型地埋管排布形式，=4。

与传统的模型相比，全尺度模型适用于整个地埋管使用年限的时−空尺度，且该模型不含任何经验假设，具备完整的理论基础。但是，该模型只适用于单个地埋管换热器，不能考虑多个钻孔之间的影响。

根据叠加原理，地下任意点的温度响应都可表示为各钻孔在该点激发的温度响应的叠加。全尺度线热源模型以单个钻孔为研究对象，为了考虑周围钻孔的影响，需加上周围钻孔在该钻孔温度响应的叠加。此时，周围钻孔可以近似为有限长线热源模型。这样，由周围−1(= 1，…，−1)个钻孔累加引起的温度响应为

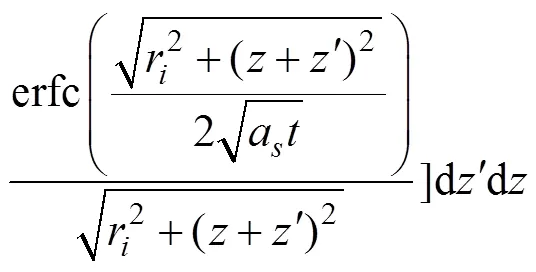
式中：为钻孔个数；i为钻孔间距离；′为沿轴的积分变量；为钻孔高度；erfc()为补余误差函数。全尺度函数拓展为以下形式：

值得注意的是：本文采用的有限长线热源模型涉及二重积分，计算量较大。CLAESSON和JAMED[25]提出1个简化表达式，将二重积分简化成一重积分。这两者是等价的，都可用在本文提出的全尺度线热源模型中。

2 结果与讨论

在给定半径和钻孔长度的比率b/、地下土壤和钻孔填充材料的热扩散率比的开方、热传导率比以及钻孔数量情况下，观察钻孔间距不同时中间位置某一钻孔的地下温度响应函数的变化。由图2和图3可知：地下温度响应函数主要受钻孔间距的影响；前期地下温度响应函数不随的变化而变化，并保持与单钻孔结果一致；中期开始较小的温度响应曲线先与单钻孔曲线分离并升高，随后各情况下的温度响应曲线都与单钻孔曲线分离并出现上升趋势；越小，温度响应曲线分离越早，上升梯度越大；越大，温度响应曲线分离越迟，上升梯度较小。当时间足够长时，地下换热过程达到近似稳态，温度响应趋于某定值。决定了达到稳态时的温度。越小，达到稳定后的地下温度响应越大；越大，达到稳定后的地下温度响应越小。另外，当接近无穷大时，温度响应曲线将不会分离而与单钻孔温度响应曲线重合。由此可见，不仅决定了分离先后和地下温度响应上升梯度，而且决定了达到稳态时温度，间距越大，热阻越小。

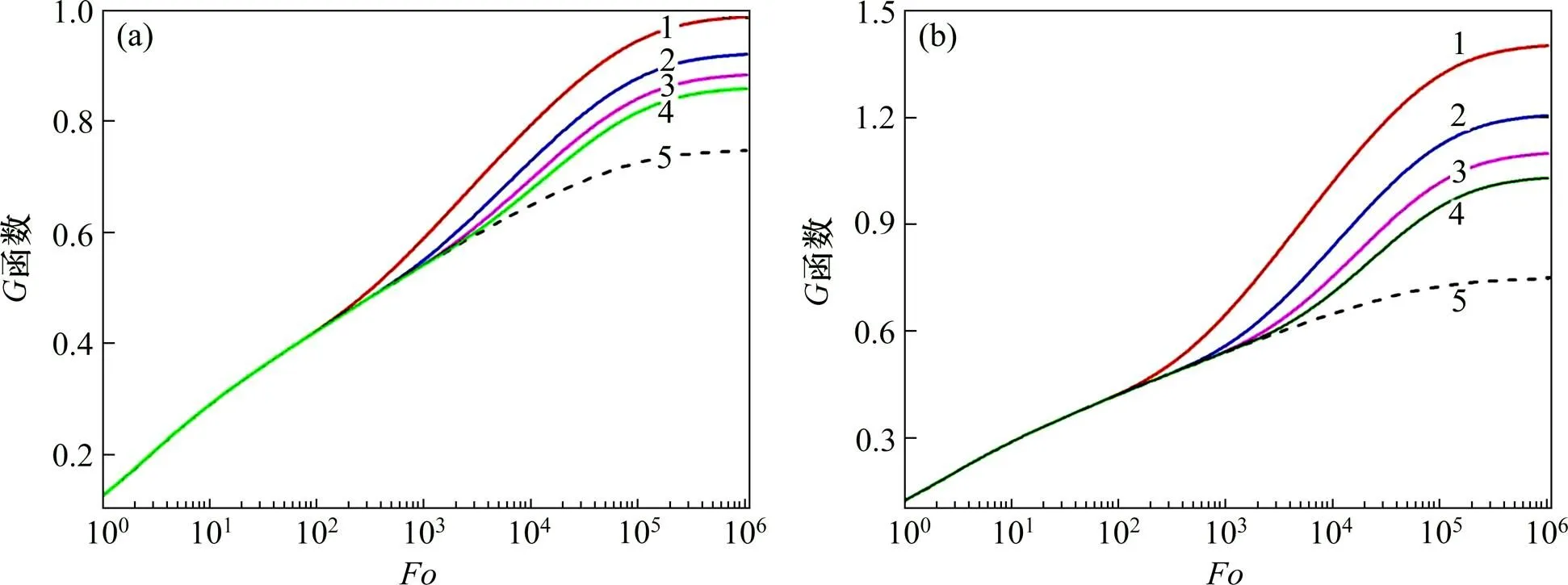
(a) 1×2单行布置；(b) 1×4单行布置

钻孔数量/个：(a) 2×2；(b) 3×3；(c) 4×4；(d) 5×5

/m：1—2；2—4；3—6；4—8；5—单钻孔。

图3 钻孔数量与间距对地埋管集群温度响应的影响

Fig. 3 Influence of borehole number and spacing on temperature responses of ground heat exchangers

在给定b/，，和时，观察不同排布方式下中间位置某一钻孔的地下温度响应函数的变化。从图4可知：地下温度响应函数主要受钻孔数量的影响；当相同时，钻孔数量越多，地下温度响应函数越大；反之，则地下温度响应函数越小。

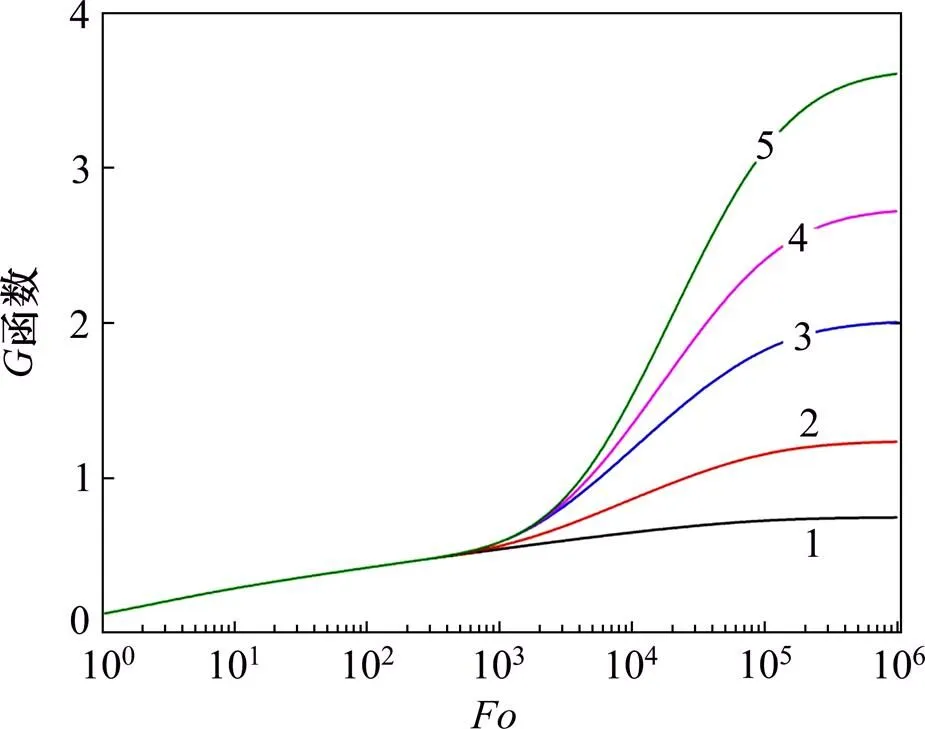
钻孔数数量/个：1—单钻孔；2—2×2；3—3×3；4—4×4；5—5×5。

对比图5中不同位置的钻孔温度响应可以发现不同位置钻孔的温度响应均不相同。中心孔的温度响应最高，这是因为中心孔散热条件最不理想；钻孔集群外围钻孔的温度响应最小，因为它的位置决定其受其他钻孔影响最小；中间位置的钻孔温度响应则介于两者之间。

实际运用时，建议选用中间位置的钻孔来近似计算平均温度，这样既能简化计算，又能满足实际工程要求。若选用中心孔作为计算参考点，则会过高估计其地下温度响应，在设计计算中，依此所得的钻孔长度比实际需求的长很多；选用钻孔集群外围的钻孔作为计算参考点时，计算的地下温度响应偏低，导致设计计算时钻孔长度达不到实际需求。这2种情况都应该避免。

短时高频温度响应不受钻孔之间换热的影响，因而，在计算短时高频温度响应时，可用原全尺度模型。但中长期的地下温度响应受钻孔换热影响较大，因此，考虑中长期的地下温度响应时必须考虑钻孔间热干扰的影响。

值得注意的是，本文提出的拓展的全尺度函数只考虑了钻孔之间距离的影响，而没考虑钻孔排布角度的影响，这样简化会不可避免地导致计算值与实际值之间存在误差。但从工程应用角度，人们关注的是地热换热器的平均温度响应，因此，这些误差应该在可接受的范围之内。另外，拓展的全尺度函数模型不能考虑其他影响因素对地下换热过程的影响，如地下渗流、水分迁移等。

(a) 钻孔数3×3个，B=4；(b) 钻孔数5×5个，B=4

3 结论

1) 拓展的全尺度线热源模型综合了复合介质线热源解有限长线热源解、无限长线热源解，既能处理地下短期、中期、长期地下换热过程，又能考虑钻孔之间换热过程的理论解。

2) 在实际工程计算中，可选用中间位置钻孔的温度来近似作为整个地下的平均温度，既能满足实际工程需要，又能简化计算。

3) 拓展的全尺度函数在考虑钻孔之间换热影响时只考虑了钻孔之间的距离，而没考虑钻孔排布角度的影响，这会不可避免地造成一定误差，但这些误差在可接受的范围之内。

[1] LI Min, LAI A C K. Review of analytical models for heat transfer by vertical ground heat exchangers (GHEs): a perspective of time and space scales[J]. Applied Energy, 2015, 151: 178−191.

[2] LI Min, LI Ping, CHAN Vincent, et al. Full-scale temperature response function (G-function) for heat transfer by borehole ground heat exchangers (GHEs) from sub-hour to decades[J]. Applied Energy, 2014, 136: 197−205.

[3] GU Yian, O'NEAL D L. Development of an equivalent diameter expression for vertical U-tubes used in ground-coupled heat pumps[J]. ASHRAE Transitions, 1998, 104(2): 347−355.

[4] SHARQAWY M H, MOKHEIMER E M, BADR H M. Effective pipe-to-borehole thermal resistance for vertical ground heat exchangers[J]. Geothermics, 2009, 38(2): 271−277.

[5] LAMARCHE L, KAJL S, BEAUCHAMP B. A review of methods to evaluate borehole thermal resistances in geothermal heat-pump systems[J]. Geothermics, 2010, 39(2): 187−200.

[6] ZENG Heyi, DIAO Nairen, FANG Zhaohong. Heat transfer analysis of boreholes in vertical ground heat exchangers[J]. Int J Heat Mass Transfor, 2003, 46(23): 4467−4481.

[7] 杨卫波, 施明恒. 二区域U型埋管传热模型及其实验验证[J]. 工程热物理学报, 2008, 29(5): 857−860. YANG Weibo, SHI Mingheng. Two-region heat transfer model of U-tube ground heat exchanger and its experiment validation[J]. Journal of Engineering Thermophysics, 2008, 29(5): 857−860.

[8] 於仲义, 陈焰华, 胡平放, 等. 基于多极理论传热模型的垂直U型地埋管传热特性研究[J]. 武汉科技学院学报, 2010, 23(3): 16−21. YU Zhongyi, CHEN Yanhua, HU Pingfang, et al. Study on heat transfer characteristic of vertical U-shape ground heat exchanges based on multiple theory of heat transfer[J]. Journal of Wuhan Institute of Science and Technology, 2010, 23(3): 16−21.

[9] INGERSOLL L R, ZOBEL O J, INGERSOLL A C. Heat conduction with engineering, geological, and other applications[M]. Madison: University of Wisconsin Press, 1954: 212−220.

[10] DEERMAN J D, KAVANAUGH S P. Simulation of vertical U-tube ground-coupled heat-pump systems using the cylindrical heat-source solution[J]. ASHRAE Transitions, 1991, 97: 287−295.

[11] CLAESSON J, ESKILSON P. Conductive heat extraction to a deep borehole-thermal analyses and dimensioning rules[J]. Energy, 1988, 13(6): 509−527.

[12] ZENG Heyi, DIAO Nairen, FANG Zhaohong. A finite line-source model for boreholes in geothermal heat exchangers[J]. Heat Transfer—Asian Research, 2002, 31(7): 558−567.

[13] LAMARCHE L, BEAUCHAMP B. A new contribution to the finite line-source model for geothermal boreholes[J]. Energy and Buildings, 2007, 39(2): 188−198.

[14] DIAO Nairen, LI Qinyun, FANG Zhaohong. Heat transfer in ground heat exchangers with groundwater advection[J]. International Journal of Thermal Sciences, 2004, 43(12): 1203−1211.

[15] 陈友明, 张训水, 杜立志, 等. 有渗流地埋管传热模型及快速算法[J]. 湖南大学学报(自然科学版), 2013, 40(1): 15−20. CHEN Youming, ZHANG Xunshui, DU Lizhi, et al. A heat transfer model of geothermal heat exchangers with hroundwater advection and its fast algorithms[J]. Journal of Hunan University (Natural Science), 2013, 40(1): 15−20.

[16] MARCOTTE D, PASQUIER P. Fast fluid and ground temperature computation for geothermal ground-loop heat exchanger systems[J]. Geothermics, 2008, 37(6): 651−665.

[17] 雷飞, 胡平放, 黄素逸. 地源热泵系统逆向建模度日数G函数法[J]. 华中科技大学学报(自然科学版), 2012, 40(3): 127−132. LEI Fei, HU Pingfang, HUANG Suyi. Degree-day G-functions approach of inverse model for ground source heat pump[J]. Huazhong University of Science and Technology (Natural Science Edition), 2012, 40(3): 127−132.

[18] BANDYOPADHYAY G, GOSNOLD W, MANN M. Analytical and semi-analytical solutions for short-time transient response ground heat exchangers[J]. Energy and Buildings, 2008, 40(10): 1816−1824.

[19] LAMARCHE L, BEAUCHAMP B. New solutions for the short-time analysis of geothermal vertical boreholes[J]. Int J Heat Mass Trans, 2007, 50(7/8): 1408−1419.

[20] YAVUZTURK C, CHIASSON A D, NYDAHL J E. Simulation model for ground loop heat exchangers[J]. ASHRAE Trans, 2009, 115(2): 45−59.

[21] CLAESSON J, JAVED S. An analytical method to calculate borehole fluid temperatures for time-scales from minutes to decades[J]. ASHRAE Trans, 2011, 117(2): 279−288.

[22] LI Min, LAI A C K. New temperature response functions (G functions) for pile and borehole ground heat exchangers based on composite-medium line-source theory[J]. Energy, 2012, 38(1): 255−263.

[23] LI Min, LAI A C K. Analytical model for short-time responses of borehole ground heat exchangers: model development and validation[J]. Applied Energy, 2013, 104: 510−516.

[24] MA Weiwu, LI Min, LI Ping, et al. New quasi-3D model for heat transfer in U-shaped GHEs (ground heat exchangers): effective overall thermal resistance[J]. Energy, 2015, 90: 578−587.

(编辑 陈灿华)

Temperature responses of ground heat exchanger clusters based on full-scale line-source solution

LI Ping1, LI Min1, MA Weiwu1, XIAO Lianrong2

(1. School of Energy Science and Engineering, Central South University, Changsha 410083, China; 2. Hunan AVA Dairy Industry Co. Ltd., Changsha 410013, China)

In order to tackle the problem of heat transfer of GHE spanning diverse time-space scales, a full-scale line-source solution was reported for heat transfer of ground heat exchanger (GHE) clusters, which was an analytical solution that was developed from the method of matched asymptotic expansions and the principle of superposition. Temperature-response curves of line- and matrix-arranged GHE clusters were presented and the impact of borehole spacing on temperature evolution in the ground was analyzed. The results show that full-scale line-source solution simplify the calculation temperature range of GHE clusters.

ground-coupled heat pumps; borehole ground heat exchanger; temperature responses function; full-scale line-source model

10.11817/j.issn.1672−7207.2017.10.035

TU833+.3

A

1672−7207(2017)10−2817−06

2016−11−12；

修回日期：2017−01−10

国家科技支撑计划项目(2012BAD12B04)(Project (2012BAD12B04) supported by the National Key Technology R&D Program of China)

李旻，博士，副教授，从事新能源和环境领域的工程热物理问题研究；E-mail: cnlimin@csu.edu.cn