基于岩体时变力学参数的深部矿段回采顺序优化

胡建华，习智琴，罗先伟，周科平，艾自华



基于岩体时变力学参数的深部矿段回采顺序优化

胡建华1，习智琴1，罗先伟2，周科平1，艾自华1

(1. 中南大学 资源与安全工程学院，湖南长沙，410083；2. 广西高峰矿业股份有限责任公司，广西南丹，547200)

基于岩体力学的时变参数演化规律，设计高峰深部矿段5种可行的回采顺序方案。运用耦合建模技术构建深部矿段复合空区的三维有限元模型，再采用FLAC3D仿真技术，实现岩体时变力学参数下不同回采顺序的时空演化规律。研究结果表明：各种回采顺序下的局部岩体最大拉应力和压应力都达到岩体的抗拉和抗压强度，应及时处理采空区；随着回采推进，顶底板位移逐渐增大，在最后1步达到最大值，并且受不同工艺的影响，最大位移表现出差异性；顶板位移最大沉降分别为50.0，38.0，74.0，64.9和70.5 mm，底板最大垂直位移(底鼓)分别为68.6，34.9，47.6，45.8和46.4 mm；岩体的破坏主要表现为剪切和拉伸塑性破坏，其中方案3和方案4的剪切破坏体积比方案1，2和5的剪切破坏体积，方案5发生拉伸破坏体积最大，方案2的整体塑性区体积比方案1的稍大。综合采场的生产能力和形变应力及其塑性破坏特征分析，选择较优的方案2。

时变力学参数；回采顺序；时变应力与变形；塑性破坏；优化

合理确定矿段内采场间的回采顺序，是实现采矿工程结构参数优化和高效安全回采的关键，特别对于深井复杂采空区下的资源安全高效回采及矿山工程稳定性具有重要的作用[1−3]。一般地，研究回采顺序优化问题，主要针对矿山不同的开采顺序方案进行简单比较和优选。如刘晓明等[1]设计了2种可行的回采顺序模拟方案，对冬瓜山深井开采的回采顺序进行了优化研究；彭康等[4]模拟计算了三山岛金矿新立矿区中段盘区间不同回采顺序，获得了不同开采步骤下的矿岩应力和位移特征值，提出了间隔2个盘区回采1个盘区的优化回采工艺方案；韩斌等[5]根据金川二矿区多中段多盘区同时回采的实际情况对7种回采顺序进行了数值模拟，发现从矿体一端向另一端渐进式下降的最佳回采顺序；甯瑜琳等[6]以玲南金矿两步骤上向水平分层充填采场为例，对比盘区交错式、凸型阶梯式、三角型阶梯式这3种回采顺序的工程响应，发现采用凸型阶梯式回采时采场稳定性最强。然而，采矿过程始终处于不断加载和卸载的过程中[7]，在不断调整再平衡过程中矿岩性质产生劣化，常规的力学参数难以反映矿岩体劣化损伤对矿岩体的响应。在采动时变演化过程中，胡建华等[8]分析了矿山开采的采动影响区域内围岩扰动弱化规律，获得了岩体力学性质和参数的劣化时变规律。李维树等[9]在高拱坝卸荷带内通过35点动静对比原位变形试验，建立了卸荷下卸荷带内的岩体变形参数与波速之间的时变关系式。王瑞红 等[10]通过对坝肩开挖边坡应力应变场的弹塑性力学进行分析，得到了每步开挖后岩体劣化参数，并实现了对坝肩槽开挖过程中的边坡稳定性分析。雷涛等[11]以铜坑矿92号矿体连续诱导崩落卸荷开挖采场为对象，基于细观损伤力学和卸荷岩体力学理论，运用 RFPA 软件建立了岩体卸荷计算的等效数值模型，据岩体卸荷损伤和声发射效应获得了卸荷岩体力学参数的变化曲线及其劣化规律。然而，在劣化时变岩体力学参数的工业应用上，人们的实践研究较少。为此，本文作者以广西高峰矿105号矿体的某深部中段矿体为研究对象，基于岩体时变力学参数，设计5种可行的回采方案进行数值模拟研究，分析矿段在不同方案中时变演化规律，提出合理的安全回采顺序。

1 工程概况

广西高峰矿的105号矿体位于100号矿体的深部延伸段，已经成为高峰矿的主要开采矿体，赋存在礁灰岩中，埋深绝对高差为800~1 000 m。该矿段受多年前的非法盗采，矿体内空区复杂，巷道众多，裂隙发育，矿岩强度较低，不稳固，深部开采的地应力高等，给矿山开采的安全性带来了极大威胁。同时，该矿山的资源品位高，价值大，为保障该矿体开采的安全性，需对矿体的整体开采顺序进行分析和确定。由于−150 m水平以上的矿体大部分已开采完毕，目前−200 m以上的开采范围主要集中在−150~−200 m，主要对该区段的整体开采顺序进行优化。

2 模型构建与方案设计

2.1 模型的建立

由矿山实际地质赋存条件和空区探测结果建立三维立体模型。为简化计算，选取105号矿体−150~ −200 m区段的矿体实际三维模型北部的部分矿体模型进行数值计算。依据圣维南原理，选择区域矿体3倍半径范围为模型边界，计算矿段实体与模型的空间三维关系，如图1(a)所示。模型长×宽×高为540 m×360 m×300 m，划分网格后共有55 236个节点，29 9421个单元，其中计算矿段网格模型见图1(b)。岩体采用Mohr-Coulomb 强度准则的弹塑性本构关系，计算模型的侧面为水平位移约束，底面固定，上表面为自由边界，并根据实测地应力以自重应力施加荷载环境参数。

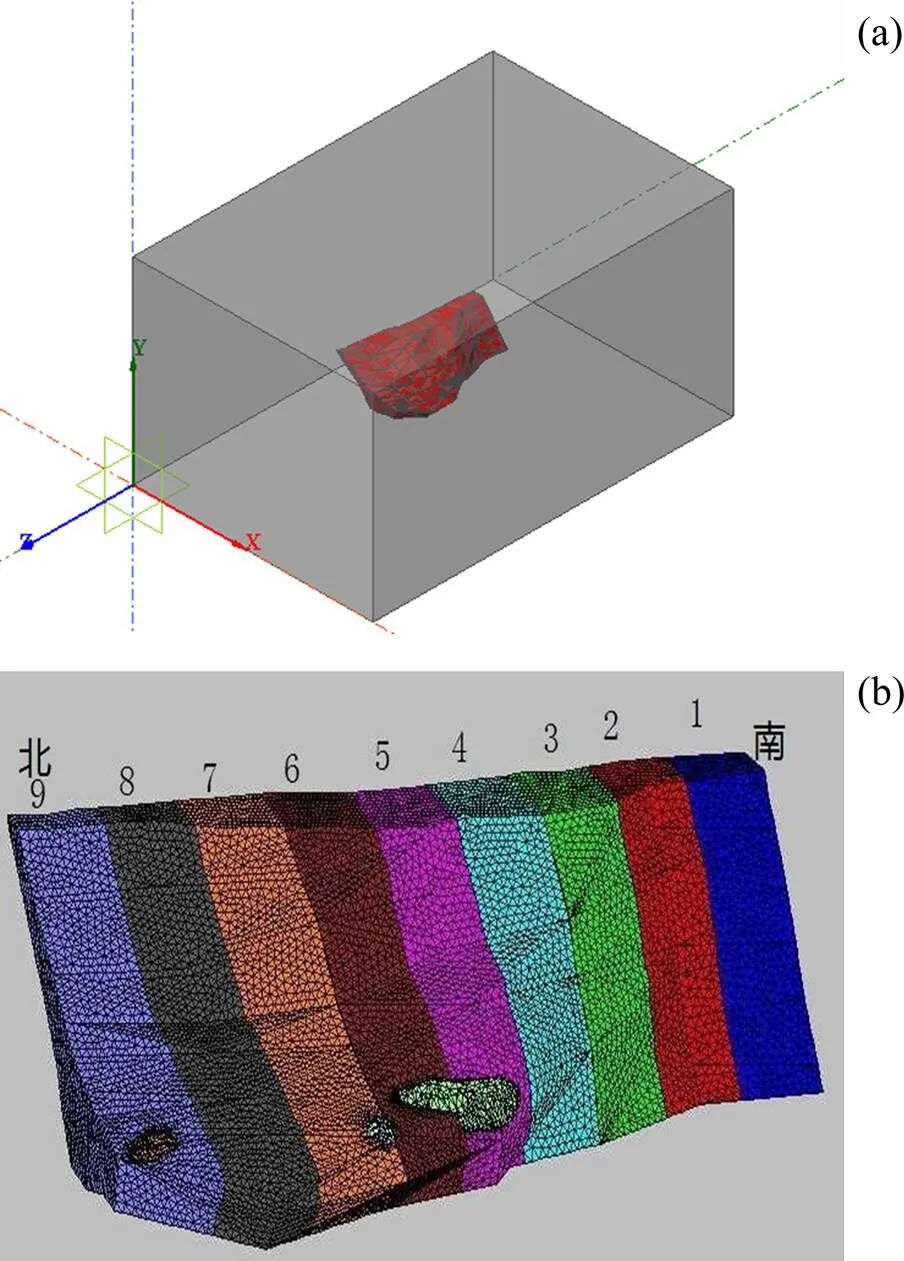
(a) 计算矿段实体模型；(b) 计算矿段网格模型

2.2 时变演化下岩体力学参数

由于地下矿山开挖过程的非线性时变特性，其最后力学状态不但取决于加载过程，而且取决于分析对象几何域或物理参数的时变特征值[12]，其岩体力学参数的时变特征值尤为关键。在开挖采矿初期，岩体参数选取初始物理力学参数，，和，见表1(其中，为体积弹性模量；为剪切弹性模量；为内摩擦角；为黏聚力)。

表1 岩体初始物理力学参数

一步骤开挖后，对已开挖采场的周边扰动影响区内采场矿岩力学参数选取时变的岩体力学参数1，1，1和1，逼近实际弱化情况，岩体时变力学参数计算式[8]如下：

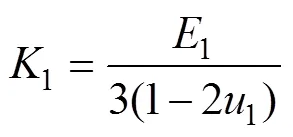
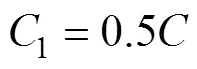
式中：1=0.5；1=1.15；为弹性模量；为泊 松比。

2.3 回采方案设计

根据回采可行方案的分析与模型特征，开挖矿体区域的编排由右向左(由南向北)依次为1~9，并对该矿段左部存在的3个空区，回采前先进行空区充填处理。设计的5种可行回采方案见表2，岩体时变力学参数计算流程见图2。

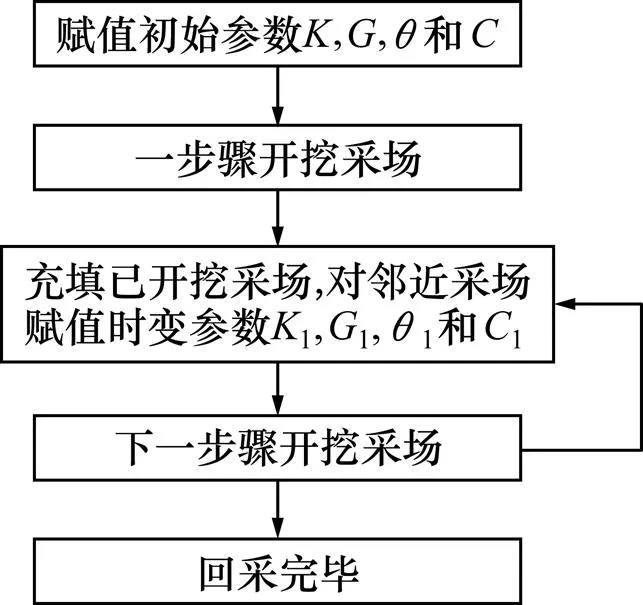
图2 岩体时变力学参数计算流程

表2 整体矿段回采方案设计

注：采1表示开采矿段1号采场；充1表示充填矿段1号采场；编号1~9采场见图1。

3 计算结果分析

3.1 时变应力场分析

随着回采与充填时步的推进，顶底板最大拉应力时变曲线整体上呈现出先增大再减小的趋势，如图3(a)所示。在方案1中出现最大拉应力，达到3.96 MPa，且开挖步数多，拉应力持续时间最长，岩体受拉产生的拉裂破坏显著；方案2，3，4和5中出现的最大拉应力分别为3.48，3.16，3.11和3.68 MPa，都达到或超过了围岩的抗拉强度；方案3和方案4在开挖完毕后的最大拉应力相对最小，因为开采方式为隔一采一，从空间上错开了开挖顺序，避免了同一开挖顺序中各采场间的相互影响。方案2的最大拉应力是方案1，2和5中最小的，这是由于随着开采向一端或两端推进，已回采完毕并充填后的采场形成了整片支撑区，相当于留有较大的支撑矿柱，最后压缩沉降。

(a) 最大拉应力；(b) 最大压应力

由最大压应力时变曲线可知：最大压应力为45.95~102.75 MPa，如图3(b)所示；方案1~5的最大压应力分别为102.75，102.60，102.20，95.64和71.74 MPa，均已达到围岩抗压强度；方案1的最大压应力最大，方案5的最小；最大压应力都出现在空区周围的边角应力集中区域，因为开挖到空区内的采场，虽然空区已经充填，但由于周围采场岩体物理力学参数弱化以及充填体的强度较低，因此，在空区周围边角出现较大应力集中现象。开挖采场后应力转移到空区周围，所以，最大压应力时变曲线整体表现出无规律性。最后一步开挖完毕后，方案1的最大压应力最小，方案2和方案4的次之，且方案二开挖步数较方案1的少。

3.2 时变位移场分析

采动引起的围岩变形与位移是导致顶板围岩发生大的形变冒落偏帮和底板底鼓的原因，影响到采场、巷道的稳定，危及作业人员安全[13]。对比顶板时变位移和底板时变位移各方案可知(如图4所示)：随着开采推进，采空区暴露面积增大，充填体强度较低，支撑能力有限，导致顶底板位移不断增加；在最后回采步时，顶底板位移都达到最大值。各方案中顶板最大位移分别为50.0，38.0，74.0，64.9和70.5 mm，底板最大垂直位移(底鼓)分别为48.6，34.9，47.6，45.8和46.4 mm。研究结果表明：方案2的顶底板位移整体上都比其他4种方案的小，且方案2的顶板最大位移和底板最大位移分别为38.0 mm和34.9 mm，是这5种方案中最小的。

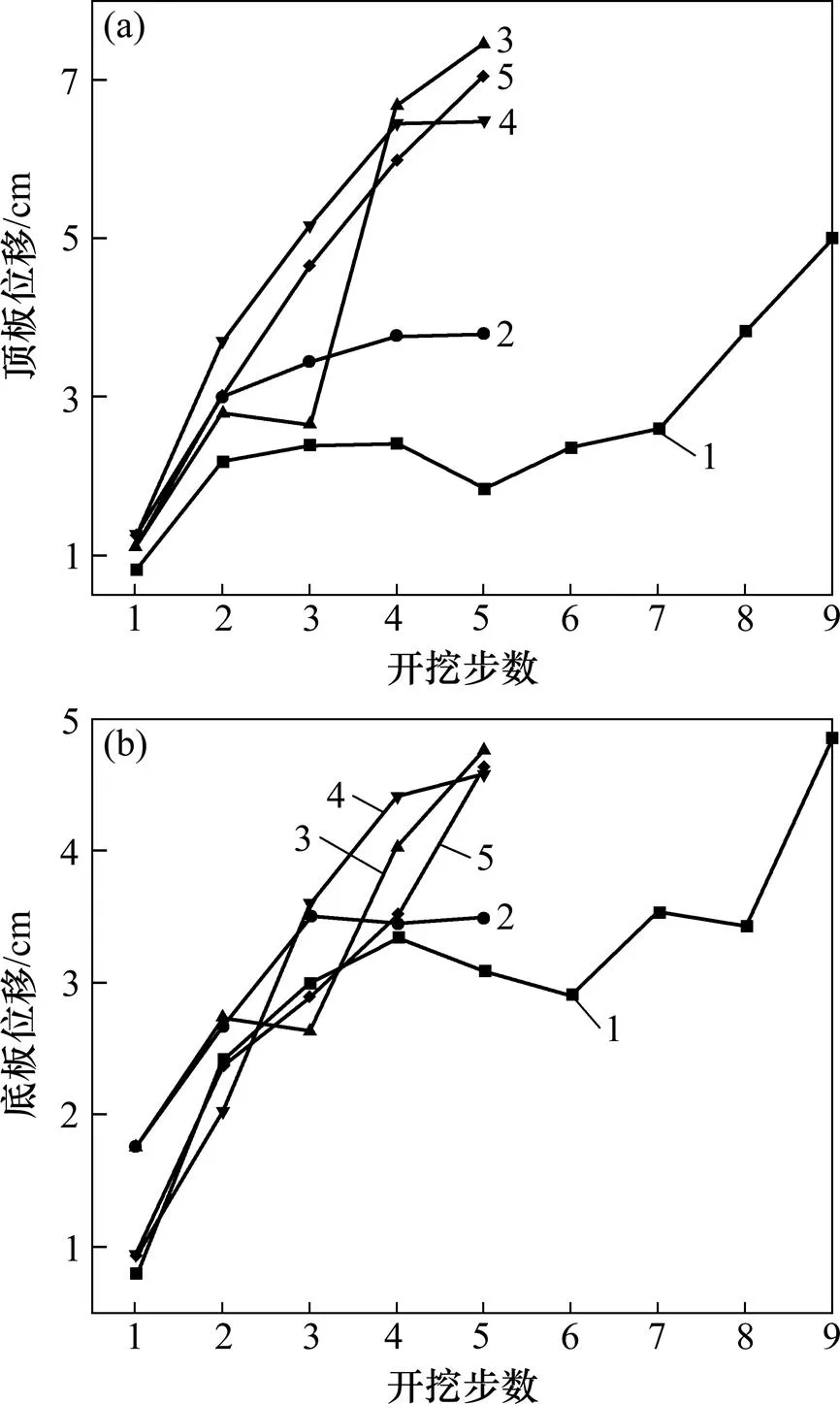
(a) 顶板；(b) 底板

3.3 塑性区分析

塑性区是开采过程中岩体达到塑性破坏的直观显示，各方案回采中典型塑性区云图如图5所示。由图5可知：在每步开挖过程中，上盘主要发生剪切破坏，而顶底板发生拉伸破坏，在靠近采场空区内矿岩体形成贯通的塑性区，并形成采场空区的塑性包络特征，如方案3、方案4和方案5；方案1和方案2的塑性区体积都在最后一步达到最大值，但没有形成绕采场的贯通区；在既有采空区内，由于受到采动的继续扰动，进一步形成大量的塑性破坏，可造成采空区的冒落和垮塌事故，必须在采动前对既有采空区进行处理。各方案的塑性区体积如表3所示。从表3可以看出：方案3和方案4的剪切破坏体积与其他3种方案相比明显过大，这与塑性区云图情况吻合；方案5中，每步骤开挖完毕后发生的剪切破坏体积和总的拉伸破坏体积都比方案1和方案2的大，方案1和方案2的剪切破坏体积和总的拉伸破坏体积处于同一数量级，方案2稍比方案1的大。

表3 不同状态的塑性区体积最大值

注：状态栏中，剪切、拉伸1和2分别为1表示“本次工况发生的塑性状态”，2表示“既有工况已经产生的塑性状态”。

3.4 方案比选

本矿段属于矿山的深部开采，为保障矿山的安全高效开采，必须提高矿山的采场开采强度和降低矿山的安全隐患。基于岩体时变力学参数的数值仿真模拟结果，方案2的应力受双向采动影响不是最小，但位移最小，塑性区没有形成采场围岩的贯通，其塑性区体积较小，并且2个采场同时生产，生产能力大，有利于强化开采和安全保障。故方案2较优。

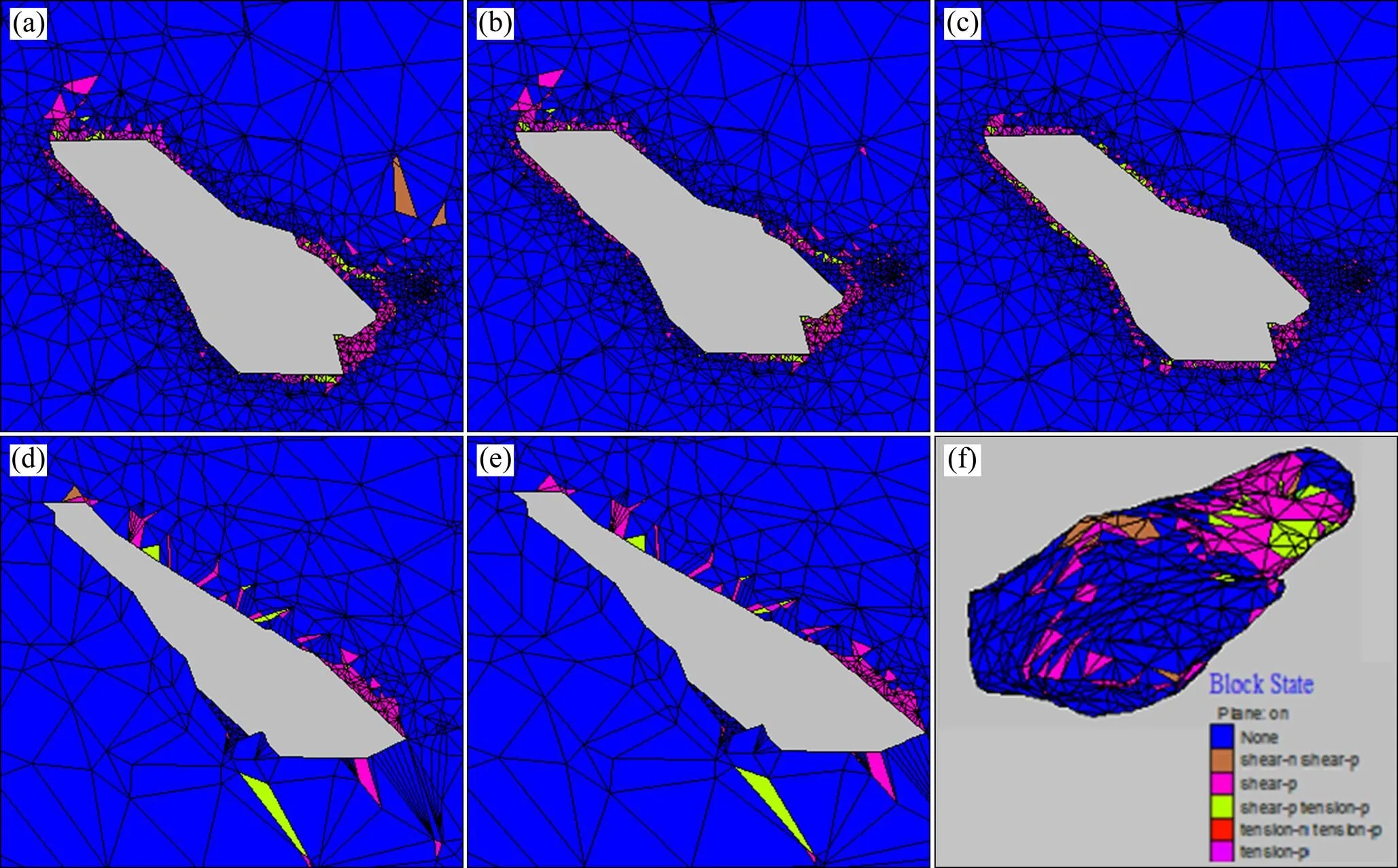
(a) 方案3；(b) 方案4；(c) 方案5；(d) 方案1；(e) 方案2；(f) 采场9空区

4 结论

1) 所设计的开采方案中，最大拉应力和最大压应力都达到了围岩的抗拉强度和抗压强度，且都发生在采场边部围岩的应力集中处；在回采前，需要对既有的采空区进行充填处理，降低扰动对既有空区的二次扰动破坏。

2) 随着开采的推进，顶底板位移逐渐增大，在最后一步达到最大值。5种方案中，方案3和4发生剪切破坏的体积比方案1，2和5的大，方案5发生拉伸破坏的体积最大；方案2和方案1的塑性区体积最大，方案2的塑性区体积比方案1的稍大。

3) 从高效安全角度出发，综合分析各方案顶底板最大拉应力、压应力、沉降位移以及各状态下的塑性区体积，方案2为最优回采顺序方案。

[1] 刘晓明, 杨承祥, 罗周全. 深井开采回采顺序数值模拟优化研究[J]. 南华大学学报(自然科学版), 2008, 22(4): 15−21. LIU Xiaoming, YANG Chengxiang, LUO Zhouquan. Numerical simulation optimization of mining sequence in deep mining[J]. Journal of University of South China (Science and Technology), 2008, 22(4): 15−21.

[2] 沈慧明, 许振华, 朱利平, 等. 残矿回采顺序优化与复杂采空区稳定性的有限元模拟研究[J]. 中国矿业, 2011, 20(1): 78−81. SHEN Huiming, XU Zhenhua, ZHU Liping, et al. Finite element simulation study on optimization of mining sequence and stability for complicated mine area[J]. China Mining Magazine, 2011, 20(1): 78−81.

[3] 施建俊, 孟海利. 采场结构参数与回采顺序的数值模拟优化研究[J]. 有色金属, 2005, 57(2): 9−11. SHI Jianjun, MENG Haili. Study on the optimization of structural parameters of stope and mining sequence[J]. Nonferrous Metals, 2005, 57(2): 9−11.

[4] 彭康, 李夕兵, 彭述权, 等. 三山岛金矿中段盘区间合理回采顺序动态模拟选择[J]. 矿冶工程, 2010, 30(3): 8−11. PENG Kang, LI Xibing, PENG Shuquan, et al. Dynamic simulation of reasonable stoping sequence in middle section of panel in Sanshandao Gold Mine[J]. Mining and Metallurgical Engineering, 2010, 30(3): 8−11.

[5] 韩斌, 吴爱祥, 刘有同, 等. 金川二矿区多中段机械化盘区回采顺序的数值模拟优化研究[J]. 矿冶工程, 2004, 24(2): 4−7. HAN Bin, WU Aixiang, LIU Youtong, et al. Optimization of mining sequences of multi-level mechanized panels of Jinchuan’s No.2 mining area through numerical method[J]. Mining and Metallurgical Engineering, 2004, 24(2): 4−7.

[6] 甯瑜琳, 梁超, 扈守全, 等. 两步骤充填采矿法回采顺序优化研究[J]. 采矿技术, 2014, 14(2): 10−13. NING Yulin, LIANG Chao, HU Shouquan, et al. Study on sequence optimization of mining method in two steps filling mining[J]. Mining Technology, 2014, 14(2): 10−13.

[7] 周科平, 古德生. 遗传算法优化地下矿山开采顺序的应用研究[J]. 中国矿业, 2001, 10(5): 50−54. ZHOU Keping, GU Desheng. Optimization of stoping sequence in underground mine by using genetic algorithm method[J]. China Mining Magazine, 2001, 10(5): 50−54.

[8] 胡建华, 雷涛, 罗先伟, 等. 矿山采动卸荷岩体力学参数劣化规律研究[J]. 岩土力学, 2012, 33(4): 1123−1128. HU Jianhua, LEI Tao, LUO Xianwei, et al. Study of mechanical parameters deterioration laws of rock mass in mining unloading[J]. Rock and Soil Mechanics, 2012, 33(4): 1123−1128.

[9] 李维树, 周火明, 陈华, 等. 构皮滩水电站高拱坝建基面卸荷岩体变形参数研究[J]. 岩石力学与工程学报, 2010, 29(7): 1333−1338. LI Weishu, ZHOU Huoming, CHEN Hua, et al. Study of unloading rock mass deformation parameters for high arch dam foundation base of Goupitan hydropower station[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(7): 1333−1338.

[10] 王瑞红, 李建林, 刘杰, 等. 考虑岩体开挖卸荷动态变化水电站坝肩高边坡三维稳定性分析[J]. 岩石力学与工程学报, 2007, 26(增1): 3515−3521. WANG Ruihong, LI Jianlin, LIU Jie, et al. Three-dimensional stability analysis of dam abutment high slope dynamic behaviors considering rock mass unloading[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(Supp 1): 3515−3521.

[11] 雷涛, 周科平, 胡建华, 等. 卸荷岩体力学参数劣化规律的细观损伤分析[J]. 中南大学学报(自然科学版), 2013, 44(1): 275−281. LEI Tao, ZHOU Keping, HU Jianhua, et al. Mechanics parameters deterioration laws of unloading rock mass by meso-damage mechanics[J]. Journal of Central South University (Science and Technology), 2013, 44(1): 275−281.

[12] 胡建华, 苏家红, 周科平, 等. 顶板诱导崩落模式选择时变数值分析[J]. 岩土力学, 2008, 29(4): 931−936. HU Jianhua, SU Jiahong, ZHOU Keping, et al. Time-varying numerical analysis of mode in induction caving roof[J]. Rock and Soil Mechanics, 2008, 29(4): 931−936.

[13] 徐文彬, 潘卫东, 刘辉. 动态扰动诱发嗣后充填采场灾变事故分析[J]. 采矿与安全工程学报, 2015, 32(1): 65−72. XU Wenbin, PAN Weidong, LIU Hui. Analysis on the catastrophe mechanism of backfill stope resulting from dynamic disturbance[J]. Journal of Mining & Safety Engineering, 2015, 32(1): 65−72.

(编辑 陈灿华)

Optimization of mining sequence based on rock mass time-varying mechanics parameters

HU Jianhua1, XI Zhiqin1, LUO Xianwei2, ZHOU Keping1, AI Zihua1

(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;2. Guangxi Gaofeng Mining Co. Ltd., Nandan 547200, China)

Based on the time-varying parameter evolution law of rock mass mechanics, five kinds of mining sequence schemes were designed in the deep section of Gaofeng mine. The 3D finite element model with the goafs was built by the coupled modeling technique in deep mine sections. Using the FLAC3D program, the evolution laws of space and time were simulated to different mining sequences based on the time-varying mechanical parameters of rock mass. The results show that the maximum values of tensile and compressive stress reach the tensile and compressive strength of rock mass. In order to ensure safety of the mining, the goafs should be handled in time. With the mining process, the displacement increases gradually in the roof and floor. The displacement reaches the maximum in the last step. In the five cases, the maximum subsidences of the roof are 50.0, 38.0, 74.6, 64.9 and 70.5 mm, and the maximum vertical displacement of the floor is 68.6, 34.9,47.6,45.8 and 46.4 mm, respectively. The plastic failure is mainly manifested in shear and tensile failure to the rock mass. For the plastic volume, the volumes of the shear failure of cases 3 and 4 are larger than those of the cases 1, 2 and 5; the volume of the tensile failure of case 5 is the largest; the volume of case 2 is slightly more than that of case 1. For comprehensive production capacity, deformation, stress and plastic damage characteristics of stope, the case 2 is the best.

time-varying mechanics parameters; mining sequence; stress and displace; plastic damage; optimization

10.11817/j.issn.1672−7207.2017.10.028

TD851

A

1672−7207(2017)10−2759−06

2016−10−30；

修回日期：2016−12−28

国家十二五科技支撑计划项目(2015BAB12B01)；国家自然科学基金资助项目(41672298)；中南大学“创新驱动计划”项目(2015CX005)(Project(2015BAB12B01) supported by the National Science and Technology Support Program during 12th Five-Year; Project(41672298) supported by the National Natural Science Foundation of China; Project(2015CX005) supported by the “Innovation Drive Plan” of Central South University)

胡建华，博士，教授，从事高效安全采矿技术与岩土工程的稳定性分析研究；E-mail：hujh21@126.com