路堤荷载下刚性桩复合地基稳定性计算

熊传祥，王艺霖，陈福全



路堤荷载下刚性桩复合地基稳定性计算

熊传祥1，王艺霖1，陈福全2

(1. 福州大学环境与资源学院，福建福州，350116；2. 福州大学土木工程学院，福建福州，350116)

通过Boussinesq公式的改进解，考虑土拱效应，计算合理的桩身被动荷载，并根据非线性地基反力法，求得桩身内力分布模式。在此基础上，结合刚性桩复合地基的失稳破坏模式，采用桩身抗弯强度控制路堤的整体稳定性，并将其换算得到的抗剪强度指标应用于极限平衡法中，得到一种以桩身内力计算为基础的路堤荷载下刚性桩复合地基稳定性计算方法。最后，将本文方法与三维数值模拟、传统的极限平衡法以及等效砂桩法等简化计算方法进行对比。研究结果表明：本文方法能有效反映路堤荷载下刚性桩复合地基失稳破坏的机理，得到较合理的路堤整体稳定安全系数。

刚性桩；复合地基；稳定性；弯曲破坏；被动荷载；桩身内力

随着我国经济社会的发展，作为现代化的交通运输通道，高速公路发挥着越来越重要的作用，在高速公路的飞速建设过程中，尤其是在软土地区，出现了许多工程问题。近年来，刚性桩在软土路基加固中得到了广泛的应用，有效解决了地基承载力不足、较大的工后沉降等问题[1]。然而在实际工程中，路堤的整体稳定性问题却没能得到足够的重视，即便是采用了刚性桩复合地基，路堤失稳破坏的事故依然时有发生。针对复合地基上路堤的整体失稳破坏机理，国内外许多学者已经做了深入的研究，总结出许多有价值的结论。MIYAKE等[2−6]通过离心模型实验，分别对柔性桩与刚性桩复合地基支承路堤的失稳破坏模式进行研究，发现桩体存在多种破坏模式，且弯曲破坏比剪切破坏更容易发生，路堤稳定性主要由桩身抗弯强度控制。HAN等[7−10]通过数值分析的方法，也得出了一致的结论。JTGD 30—2015“公路路基设计规范”[11]新增了刚性桩加固软土路基的稳定性计算方法，弥补了旧规范的空白，但其指导思想仍是“采用圆弧滑动面法验算，滑动面上的抗剪强度采用桩土复合抗剪强度”。这种传统的极限平衡法，仅考虑了桩体的剪切破坏模式，可能会高估路堤的整体稳定性。郑刚等[12]结合KITAZUME等[4, 13]的研究成果，提出了等效抗剪强度法，假设桩体弯曲破坏发生于滑动面处，桩身被动荷载的等效集中水平力作用在滑动面以上桩长2/3深度，根据桩身的抗弯强度换算得到桩身的可使用抗剪强度，但这种方法没有考虑桩身被动荷载的真实分布和桩后土体的支撑作用。JGJ 79—2012“建筑地基处理技术规范”[14]引入了等效砂桩法[12]，将胶结材料的抗剪强度指标按照桩体断裂后滑动面材料的摩擦性能确定，这种方法提供了足够的冗余度，降低了设计风险，但并未体现刚性桩的真实稳定性贡献，是一种偏于保守的设计方法。目前，从刚性桩复合地基失稳破坏的机理出发，通过合理的桩身内力分布模式，计算桩体对路堤整体稳定性的真实贡献，进而评价刚性桩复合地基稳定性的计算方法尚未见报道。本文作者在单(排)桩的条件下，从路堤荷载下刚性桩复合地基失稳破坏的机理出发，以Boussinesq公式的改进解[15]为基础，考虑土拱效应，得到合理的桩身被动荷载，通过非线性地基反力法求解桩身内力的分布模式，考虑桩体的弯曲破坏，根据其抗弯强度指标计算桩体对路堤整体的真实稳定性贡献，得到了一种以桩身内力分布模式的计算为基础的稳定性计算方法。最后，建立具有代表性的简化计算模型，通过与三维数值模拟、传统的极限平衡法以及等效砂桩法等简化计算方法的对比，验证方法的适用性与可靠性。

1 考虑土拱效应的桩身被动荷载 计算

RONDOLPH等[16]强调，在桩身内力求解中，首先要得到合理的桩身被动荷载。因此，需要考虑桩身被动荷载的传递规律：在路堤荷载的作用下，由于桩土的相互作用，桩后土体的水平位移将引起土拱效应，土中荷载通过土拱向桩身传递。

图1 Ito计算方法示意图

在求解桩身被动荷载之前，首先需要计算路堤荷载下处的水平附加应力。工程上常采用的朗肯理论存在较多不足，为得到更合理的计算结果，本文采用Boussinesq公式的改进解[15]作为推导的理论基础：

式中：为坐标原点处的垂直集中力。

假设均布荷载作用于的矩形范围内，如图2所示。

由式(1)可知：在×的矩形范围内，土体单元dd对点产生的水平附加应力为

由于路堤堆载长度远大于桩间距，可认为均布荷载长度l无限长，对式(2)进行积分，可以得到l趋于无穷时，均布荷载P作用下M点的水平附加应力为

同理，可以得到矩形范围内存在三角形及梯形等形式荷载作用下点的水平附加应力。故通过上述理论，可以得到的路堤荷载下边上的水平附加应力()，则边上水平方向的总应力为

式中：为土体重度；0为静止土压力系数，0≈1−sin。

由式(4)可知边上的水平力为

将作为推导起始边界，首先针对具有相同物理边界条件的进行分析，如图3所示。

根据塑性变形理论，图中或边上法线方向的作用力σ可由下式求得

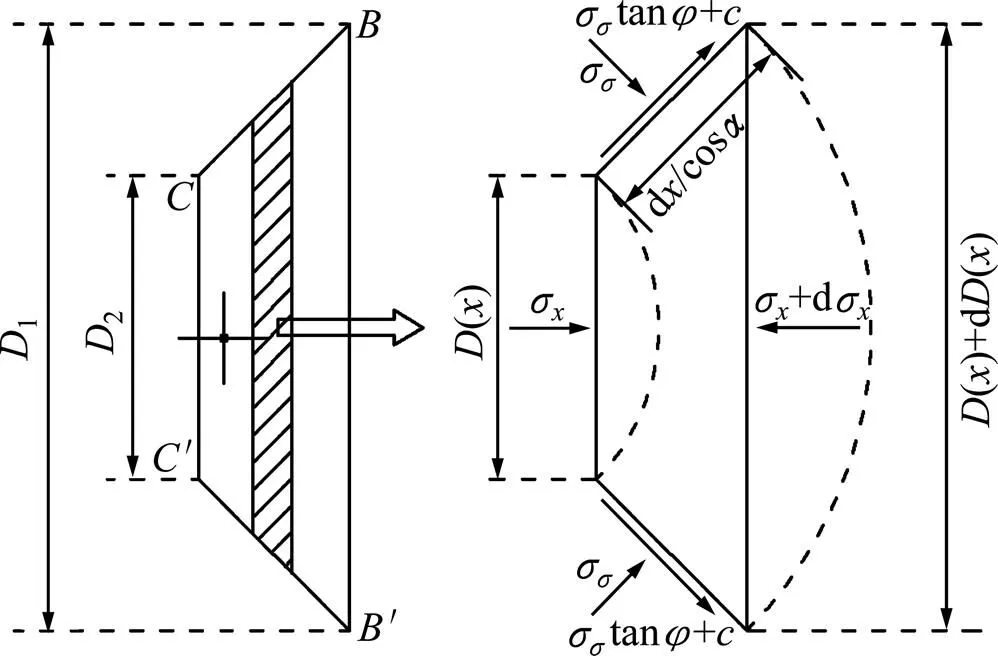
图3 CBB'C'区域土体微单元示意图

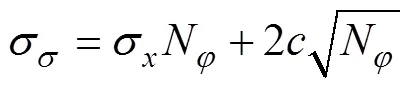
在区域范围内，土体在方向受力平衡，可得

联立式(6)~(8)，可得

(2≤≤1) (9)

当=1时，即为路堤荷载下边上水平方向的总应力，即与式(4)可以求得相同的结果，联立求解积分待定常数1，可以得到

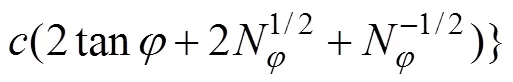
同理，取范围内的土体单元进行分析，其推导得到的结果与式(10)取=2时的表达相同的物理量，联立可得

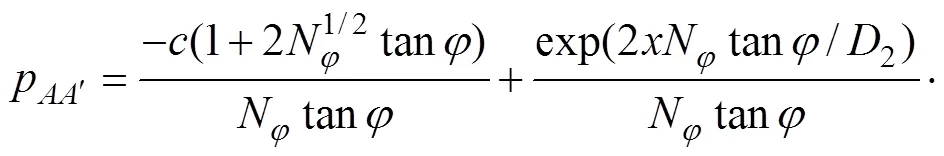
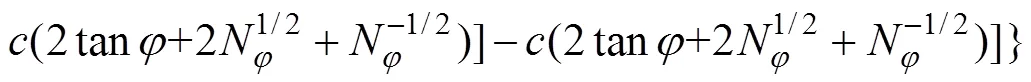
显然，边上的水平力为

因此，可求得路堤荷载下的桩身被动荷载

2 路堤荷载下刚性桩桩身内力求解

线弹性地基反力法没有考虑土体的连续性，不能真实地反映土体变形的非线性，仅在小荷载和小位移的情况下适用[20]，而非线性地基反力法中的–曲线法因其计算的合理性，在目前得到了广泛的应用。由于–曲线法的取值与计算较为复杂，HSIUNG[21]在MATLOCK[22]和REESE等[23]研究的基础上，对–曲线法进行简化，假设单位桩长的土反力在土体屈服前与水平位移呈线性关系，在土体屈服后为常数。

本文采用吴恒立[24]提出的双参数法表示地基反力系数，分别得到塑性段与弹性段的挠曲线微分方程，塑性段可通过常规方法求得桩身响应的解析解，弹性段可采用有限差分法求得桩身响应的半解析解。简化分析模型如图4所示，桩身被动荷载()已由前文计算得到，土体的屈服从地面开始向下发展，塑性段的长度为1。

桩周土反力与桩身水平位移的关系如图5所示，土体弹性状态时的土反力与桩身水平位移成正比，在塑性状态时则为常数。

故塑性段与弹性段的土反力与水平位移的关系可分别表示为

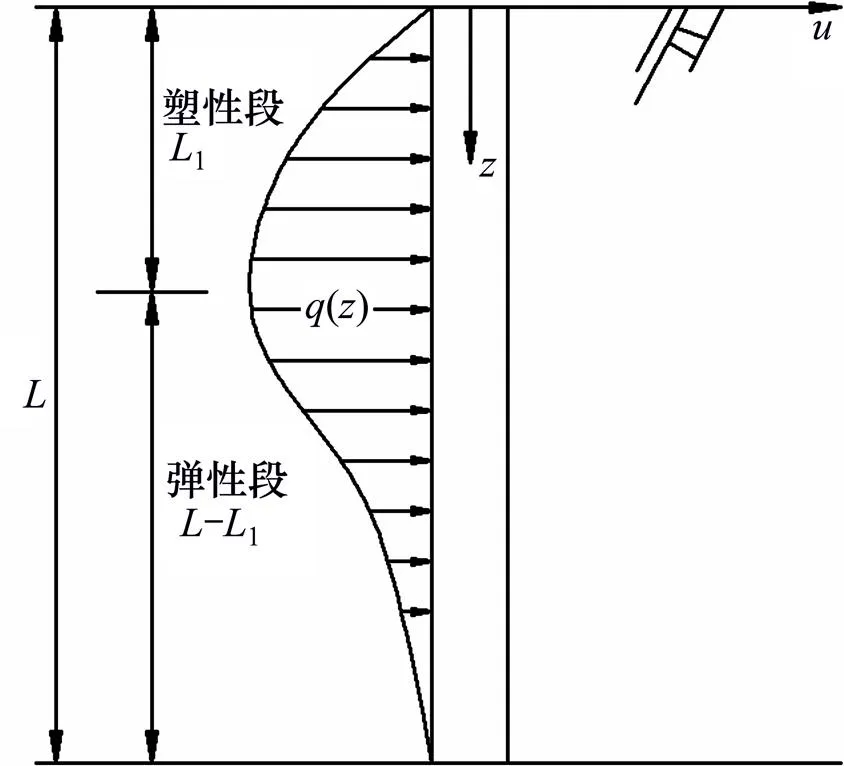
图4 刚性桩计算模型

图5 土反力与水平位移的关系

式中：u和e分别为桩身塑性段与弹性段单位桩长上的土反力；*为土体屈服位移；e为桩身弹性段的水平位移；和为双参数法中的比例参数；为桩身宽度。

基于梁的受力变形弯曲理论，桩身塑性段的挠曲线微分方程为

式中：为桩的抗弯刚度；为桩身弹性模量；为截面惯性矩；p为桩身塑性段的水平位移。通过常规方法，即求得桩身塑性段响应的解析解：

式中：p，p，p和p分别为塑性段桩身的剪力、弯矩、转角和水平位移；2和3为积分待定常数。

同理，桩身弹性段的挠曲线微分方程为

对于弹性段，无法采用常规方法，现选用有限差分法进行求解。将桩身弹性段离散为段，每段长度为Δ，为得到完整的差分方程，需要在桩身弹性段的顶部和底部分别增加2个虚拟节点，各节点的水平位移为ei，如图6所示。

对式(17)做差分变换，可以得

将0~分别代入式(18)即可得到各点的差分方程：

由桩身的连续性条件，弹性段顶部的桩身响应与塑性段底部完全相同，则有

且在弹性段与塑性段分界处，桩身水平位移达到了土体屈服位移，故

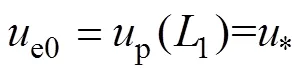
由于后文算例的桩端约束条件为桩底固定，故在此仅给出桩底固定的边界条件

由几何条件可知，Δ均可表示为

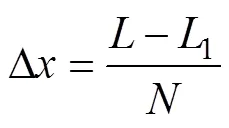
联立式(17)，(19)~(23)，即可求得积分常数和、桩身塑性段长度1以及弹性段各节点的水平位移ei，在此基础上，可以得到相应节点处的转角、弯矩和剪力：

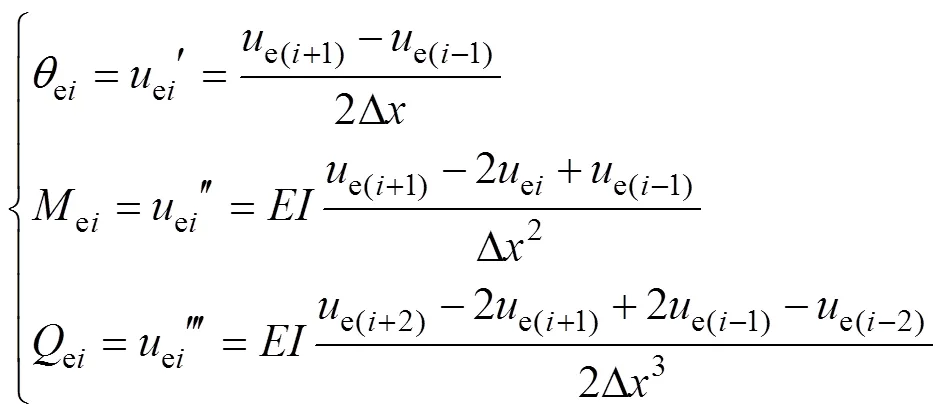
3 基于刚性桩求解的稳定性计算 方法

郑刚等[12]在KITAZUME等[4, 13]的研究基础上，提出了等效抗剪强度法，假设桩身被动荷载的等效集中水平力作用在滑动面以上桩长2/3深度处，且全部由桩体承受，根据桩身的抗弯强度换算得到桩身的可使用抗剪强度，在此基础上采用极限平衡法进行稳定性分析。但是，这种方法没有考虑桩身被动荷载的真实分布模式和桩后土体的支承作用，简单地认为桩身内力的等效集中力位于滑动面以上桩长2/3深度是不合理的。

因此，本文通过桩身被动荷载的计算，由非线性地基反力法得到了桩身内力的真实分布模式，在此基础上，近似认为桩体弯曲破坏深度位于圆弧滑动面上，考虑桩体的弯曲破坏，桩身内力的极限值由桩身抗弯强度决定，另一方面，刚性桩对路堤整体稳定性的贡献是由滑动面以上的桩身内力提供，可以将其等效为滑动面处桩身截面的抗剪强度所提供，并将此等效抗剪强度称为可使用抗剪强度[12]，结合圆弧滑动面，便可采用极限平衡法对路堤的整体稳定性进行分析计算，简化计算模型如图7所示。

图7 稳定性计算方法示意图

考虑桩体可能优先发生的弯曲破坏，滑动面以上桩身内力的极限值由桩身抗弯强度控制，即

式中：U为桩身抗弯强度，与桩身截面及材料属性相关，可根据相关规范[25]计算得到；()为前文计算得到的桩身内力分布模式；为假定的桩身内力标量；0为滑动面处桩身截面距地面的深度。

滑动面以上桩体对路堤整体的稳定性贡献为

式中：为滑动面圆心与桩顶水平面的距离。

由滑动面处桩身截面的可使用抗剪强度所提供的稳定性贡献为

式中：为滑动面处桩身截面切线与水平面的夹角；τ为可使用抗剪强度；为桩身横截面积。

考虑桩体可能优先发生的弯曲破坏，将滑动面以上桩体所提供的稳定性贡献等效为可使用抗剪强度的稳定性贡献，即

1=2(28)

由几何条件可知

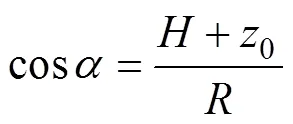
由式(25)~(29)即可求得滑动面处桩体的可使用抗剪强度τ，结合传统的极限平衡法，采用桩体的可使用抗剪强度指标，即可对路堤的整体稳定性进行分析计算。

4 不同稳定性分析计算方法的对比

路堤荷载下刚性桩复合地基可能存在多种失稳破坏模式，而目前常用的稳定性计算方法采用桩体的抗剪强度指标，仅考虑桩体的剪切破坏，可能会高估路堤的整体稳定性。JGJ 79—2012“建筑地基处理技术规范”引入了等效砂桩法，将胶结材料的抗剪强度指标按照桩体断裂后滑动面材料的摩擦性能确定，这种计算方法没有考虑刚性桩自身的抗弯能力，是一种偏保守的简化计算方法，并未反映刚性桩复合地基的真实失稳破坏机理。因此，本文在求解合理的桩身内力分布模式的基础上，考虑桩体可能优先发生的弯曲破坏，结合目前常用的极限平衡法，提出了一种基于桩身内力计算的路堤整体稳定性计算方法。

现针对刚性桩复合地基支承路堤，建立合理的简化模型，选取不同算例，分别采用三维数值模拟、传统的极限平衡法、等效砂桩法等方法进行路堤整体稳定性分析计算，并与本文方法的计算结果进行对比，分析不同方法的合理性与可靠性。

4.1 计算模型与算例

考虑计算方法的通用性，本文参照相关工程实例，建立了简化的单(排)桩计算模型。路堤取单向四车道的宽度18 m，高度为8 m，坡率为1:1.5，地基土层为典型的上软下硬的形式，计算模型剖面与截面分别如图8和图9所示。

天然地基采用素混凝土桩进行加固，桩体穿透软土层，进入硬土层，桩长为12 m，桩径为0.5 m，桩间距为1.5 m，路堤填土与下部软硬土层的物理力学参数如表1所示。表1中为土体重度；和分别为土体固结不排水条件下的黏聚力与内摩擦角；S为土体压缩模量；为土体泊松比。

单位：m

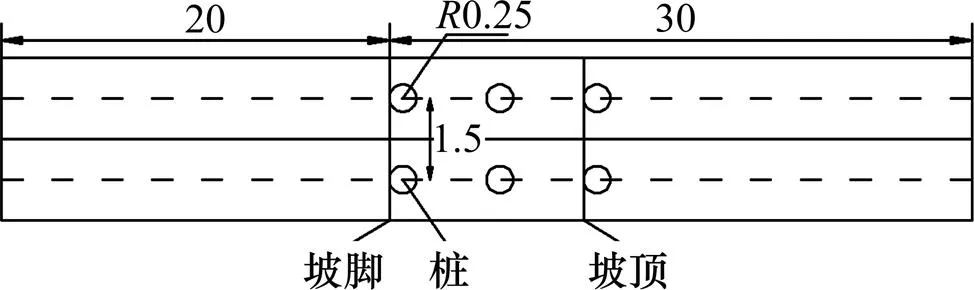
单位：m

表1 各土层物理力学参数

计算模型中，分别设置桩体位于坡脚、坡中部以及坡顶，分析不同计算方法的适用性，考虑无桩的天然地基以及桩体分别采用C20~C80不同强度等级的混凝土。其中，素混凝土桩的极限抗弯承载力与极限抗剪承载力可根据相关规范[24]进行计算，如表2所示。

4.2 对比分析

根据建立的简化计算模型，分别采用三维数值模拟、传统的极限平衡法、JGJ 79—2012“建筑地基处理技术规范”引入的等效砂桩法以及本文方法对刚性桩复合地基上路堤的整体稳定性进行分析。

表2 素混凝土桩强度参数

其中，在三维数值模拟中，采用大型有限元软件ABAQUS；在等效砂桩法中将混凝土视为与砂桩类似的散体材料[14]，不考虑桩体的黏结强度，取混凝土材料的摩擦因数为0.55，相应的折算内摩擦角为29°；采用Mathematica对桩身内力分布模式进行计算，可参照吴恒立[24]的相关研究成果，双参数法中比例系数取2 000 kN/m3+n，指数取1.6，得到桩身的可使用抗剪强度，如表3所示。

表3 各算例的桩身可使用抗剪强度

在计算过程中，算例3即素混凝土桩位于坡顶加固的情况，路堤出现了浅层滑动，因此并无对比意义；其中，算例1与算例2的计算结果非常接近，取得了相近的加固效果，故选取算例1对计算结果进行说明。分别将算例1中各方法计算得到的路堤整体稳定安全系数绘制于图中，其中C0代表无桩情况下的天然地基，如图10所示。

通过计算结果的对比可以发现，我国目前常用的极限平衡法取得了过大的安全系数，将会显著高估路堤的整体稳定性；JGJ 79—2012“建筑地基处理技术规范”引入的等效砂桩法忽略了桩身抗弯强度，得到的安全系数偏于保守且与桩身强度参数无关，与未加固的天然地基计算得到的结果较为接近，未能体现刚性桩的真实稳定性贡献；本文方法通过合理的桩身内力分布模式的计算，得到的整体稳定安全系数与三维数值模拟较为接近，得到了合理的稳定安全系数，体现了刚性桩复合地基的失稳破坏机理以及桩体的真实稳定性贡献。

1—传统的极限平衡方法；2—三维数值模拟；3—等效砂桩法；4—本文计算方法。

5 结论

1) 针对刚性桩复合地基上路堤的稳定性问题，我国目前常用的极限平衡法采用桩身的抗剪强度指标，没有考虑桩体可能优先发生的弯曲破坏，往往会高估路堤的整体稳定性；JGJ 79—2012“建筑地基处理技术规范”引入的等效砂桩法忽略了桩身的抗弯强度，未能体现刚性桩的真实稳定性贡献；考虑到三维数值模拟建模较为复杂，工程上缺乏一种针对刚性桩复合地基稳定性问题，能够反映路堤真实失稳破坏模式的简便计算方法。

2) 从路堤荷载下刚性桩复合地基失稳破坏的机理出发，立足于桩身内力分布模式的计算，有效完善了等效抗剪强度法中桩身内力分布假设不合理等问题。在此基础上，考虑桩体可能优先发生的弯曲破坏，体现了刚性桩的真实稳定性贡献。但本文计算是在单(排)桩的基础上进行的，需要继续完善合理的群桩条件下的稳定性计算方法。此外，桩间土可能发生绕流破坏，在实际工程中同样值得关注。

[1] 龚晓南. 地基处理技术及发展展望[M]. 北京: 中国建筑工业出版社, 2014: 295−301. GONG Xiaonan, Development and prospect of ground improvement technology[M]. Beijing: China Architecture and Building Press, 2014: 295−301.

[2] MIYAKE M, AKAMOTO H, WADA M. Deformation characteristics of ground improved by a group of treated soil[C]//Centrifuge 91. Rotterdam: Balkema, 1991: 295−302.

[3] HASHIZUME H, OKOCHI Y, DONG J, et al. Study on the behavior of soft ground improved using deep mixing method[C]//Proc of the International Conference on Centrifuge 98. Tokyo, Japan, 1998: 851−856.

[4] KITAZUME M, OKANO K, MIYAJIMA S. Centrifuge model tests on failure envelope of column type deep mixing method improved ground[J]. Soils and Foundations, 2000, 40(4): 43−55.

[5] 郑刚, 李帅, 刁钰. 刚性桩复合地基支承路堤稳定破坏机理的离心模型试验[J]. 岩土工程学报, 2012, 34(11): 1977−1989. ZHENG Gang, LI Shuai, DIAO Yu. Centrifugal model tests on failure mechanisms of embankments on soft ground reinforced by rigid piles[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(11): 1977−1989.

[6] 黄俊杰. 路堤下素混凝土桩复合地基变形失稳机理与注浆加固试验研究[D]. 成都: 西南交通大学土木工程学院, 2014: 54−87. HUANG Junjie. Study on failure mechanisms and grouting reinforcement of composite foundation with plain concrete piles under embankment[D]. Chengdu: Southwest Jiaotong University. School of Civil Engineering, 2014: 54−87.

[7] HAN J, HUANG J, PORBAHA A. 2D Numerical modeling of a constructed geosynthetic-reinforced embankment over deep mixed columns[C]//ASCE GSP 131, Contemporary Issues in Foundation Engineering. Austin, Texas, USA, 2005: 1−11.

[8] NAVIN M P, FILZ G M. Numerical stability analyses of embankments supported on deep mixed columns[C]//ASCE GSP 152, Ground Modification and Seismic Mitigation. Shanghai, China, 2006: 1−8.

[9] 吴春秋, 肖大平. 复合地基加固路堤的稳定性分析[J]. 岩土力学, 2007, 28(S1): 905−908. WU Chunqiu, XIAO Daping. Stability analysis of embankment on composite subgrade[J]. Rock and Soil Mechanics, 2007, 28(S1): 905−908.

[10] 刘力. 刚性桩加固路堤稳定分析方法研究[D]. 天津: 天津大学建筑工程学院, 2010: 29−71. LIU Li. Research on the stability analysis of rigid pile supported embankment[D]. Tianjin: Tianjin University. School of Civil Engineering, 2010: 29−71.

[11] JTGD 30—2015. 公路路基设计规范[S]. JTGD 30—2015. Specifications for design of highway subgrades[S].

[12] 郑刚, 刘力, 韩杰. 刚性桩加固软弱地基上路堤稳定性问题(Ⅱ): 群桩条件下的分析[J]. 岩土工程学报, 2010, 32(12): 1811−1820. ZHENG Gang, LIU Li, HAN Jie. Stability of embankment on soft subgrade reinforced by rigid inclusions (Ⅱ): group piles analysis[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(12): 1811−1820.

[13] 陈祖煜. 土质边坡稳定分析: 原理·方法·程序[M]. 北京:中国水利水电出版社, 2003: 215−224. CHEN Zuyu. Soil slope stability analysis: theory, methods and programs[M]. Beijing: China Water Power Press, 2003: 215−224.

[14] JGJ 79—2012. 建筑地基处理技术规范[S]. JGJ 79—2012. Technical code for ground treatment of buildings[S].

[15] 王广月. 地下结构局部超载侧压力计算[J]. 岩土工程技术, 1997(1): 35−40. WANG Guangyue. Lateral pressure calculation of underground structure with local surcharge[J]. Geotechnical Engineering Technique, 1997(1): 35−40.

[16] RANDOLPH M F, HOULSBY G T. The limiting pressure on a circular pile loaded laterally in cohesive soil[J]. Géotechnique, 1984, 34(4): 613−623.

[17] ITO T, MATSUI T. Methods to estimate lateral force acting on stabilizing piles[J]. Soils and Foundations, 1975, 15(4): 45−59.

[18] 竺明星, 龚维明, 何小元, 等. 堆载作用下考虑土拱效应的被动桩变形内力半解析解[J]. 岩土工程学报, 2013, 35(11): 1997−2008. ZHU Mingxing, GONG Weiming, HE Xiaoyuan, et al. Semi-analytical solution to deformation and internal force of passive piles under surcharge loads considering soil arching effect[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(11): 1997−2008.

[19] 李忠诚, 杨敏. 被动桩土压力计算的被动拱−主动楔模型[J]. 岩石力学与工程学报, 2006, 25(S2): 4241−4247. LI Zhongcheng, YANG Min. Passive arching−active wedge model of soil pressure calculation in passive piles[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S2): 4241−4247.

[20] 张忠苗. 桩基工程[M]. 北京: 中国建筑工业出版社, 2007: 246−282. ZHANG Zhongmiao. Pile foundation engineering[M]. Beijing: China Architecture and Building Press, 2007: 246−282.

[21] HSIUNG Y M. Theoretical elastic-plastic solution for laterally loaded piles[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2003, 129(5): 475−480.

[22] MATLOCK H. Correlations for design of laterally loaded piles in soft clay[C]//Proceeding of the 2nd Annual Offshore Technology Conference. Houston, Texas, USA, 1970: 577−594.

[23] REESE L C, COX W R, KOOP F D. Analysis of laterally loaded piles in sand[C]//Proceeding of the Sixth Annual Offshore Technology Conference. Houston, Texas, USA, 1974: 473−483.

[24] 吴恒立. 推力桩计算方法的研究[J]. 土木工程学报, 1995, 28(2): 20−28. WU Hengli. Study on calculation method of laterally loaded pile[J]. China Civil Engineering Journal, 1995, 28(2): 20−28.

[25] GB 50010—2010. 混凝土结构设计规范[S]. GB 50010—2010. Code for design of concrete structure[S].

(编辑 杨幼平)

Stability calculation of rigid pile composite foundation under embankment load

XIONG Chuanxiang1, WANG Yilin1, CHEN Fuquan2

(1. College of Environment and Resources, Fuzhou University, Fuzhou 350116, China;2. College of Civil Engineering, Fuzhou University, Fuzhou 350116, China)

Considering soil arching effect, the reasonable passive load of rigid pile was deduced from the modified formula of Boussinesq, and the distribution of pile’s internal force could be drawn by nonlinear subgrade reaction method. Based on this, the allowable shear strength controlled by bending strength of pile was obtained, and then applied was to limit equilibrium method. Above all, a calculation method for stability of rigid pile composite foundation under embankment load was suggested based on calculation of pile internal force. Finally, a comparison was done among this mothod with 3D numerical simulation method，traditional limit equilibrium method and the equivalent sand pile method. The results show that failure mechanisms of rigid pile composite foundation under embankment load can be effectively reflected and more reasonable safety factors of embankment can be obtained through the proposed method.

rigid pile; composite foundation; stability; bending failure; passive load; pile internal force

10.11817/j.issn.1672−7207.2017.10.026

TG146.2

A

1672−7207(2017)10−2745−08

2016−10−09；

修回日期：2017−01−24

国家自然科学基金资助项目(41272299)(Project (41272299) supported by the National Natural Science Foundation of China)

陈福全，博士，教授，从事岩土工程研究；E-mail：phdchen@fzu.edu.cn