基于免疫粒子群算法的中央空调冷冻水系统优化控制

陈大鹏，张九根，梁 星

(1.南京工业大学 电气工程与控制科学学院，南京 211800； 2.南京工业大学 智能建筑研究所，南京 211800)(*通信作者电子邮箱zjgnjtech@163.com)

基于免疫粒子群算法的中央空调冷冻水系统优化控制

陈大鹏1,2，张九根1,2*，梁 星1,2

(1.南京工业大学 电气工程与控制科学学院，南京 211800； 2.南京工业大学 智能建筑研究所，南京 211800)(*通信作者电子邮箱zjgnjtech@163.com)

为了降低中央空调的运行能耗并对冷冻水回水温度进行稳定而有效的控制，提出了一种冷冻水回水温度优化控制方法，根据回水温度测量值与设定值间的偏差判断室内实际负荷需求。首先，对粒子群优化(PSO)算法中的惯性权重采用呈指数形式下降的策略，使微粒更新速率能够适配寻优过程的各个阶段；然后,针对模型参数存在不确定摄动的问题，引入人工免疫(AI)思想形成免疫粒子群算法，从而拓展微粒的多样性，增强其摆脱局部最优值的能力；最后，据此优化比例积分微分(PID)控制器的3个参数，并通过该控制器调节冷冻水泵的频率，将实际回水温度保持在设定值附近。实验结果表明，采用该控制策略在满足室内负荷需求的前提下能够更有效地降低冷冻水泵的运行频率，节能效果与控制质量更佳。

回水温度；比例积分微分控制器；粒子群优化算法；人工免疫算法；节能

0 引言

据统计，建筑能耗约占社会总能耗的27.4%，而中央空调的耗电量约占建筑总能耗的50%～70%[1]。传统中央空调系统在设计时通常按最大负荷来设计，而绝大多数空调系统在70%以上的时间内均是在部分负荷下运行[2]。此外，由于其控制过程中不确定因素众多，还具有时滞、时变、非线性等特征，难以建立精确的数学模型[3]，故如何提高中央空调系统的控制质量与节能效果一直是人们所关注的问题。

目前，国内外针对中央空调系统节能控制的研究已较多。文献[5]为冷冻水系统建立了动态数学模型，并利用比例积分微分(Proportional Integral Differential, PID)控制来调节冷冻水泵的频率，结果表明引入控制器后，中央空调的节能率可达到33.9%。近年来，随着智能控制技术的不断发展，神经网络、模糊控制等也常用于解决PID控制过程中参数整定困难、受模型不确定因素影响大等问题[4]。

为了更好地跟踪回水温度设定值，文献[6]设计了模糊PID控制器，增强了系统的抗扰动能力。文献[1]将自适应模糊PID控制应用于回水温度控制系统中，虽然调节时间变长，但是冷冻水流量波动却更为稳定。文献[7]将遗传PID控制应用于室内温度控制系统中，并分别比较了遗传PID算法、PID算法与神经网络PID算法的延迟时间与调节时间。文献[8]为中央空调系统设计了模糊预测控制器，并通过现场总线技术加以实现，使得系统能够全方位地提高节能率并保持稳定运行。文献[9]采用粒子群(Particle Swarm Optimization, PSO)算法优化径向基神经网络的初始参数，并据此调整PID控制器参数，实现了变静压设定值控制，具有较好的跟踪精度与节能效果。由于PID控制器结构简单，对硬件设备要求低，在工程上还不能完全被取代，故利用智能算法优化PID控制器参数，提高其控制性能并应用于现实对象上是目前研究的热点。

本文通过对PSO算法中的惯性权重采用呈指数形式下降的策略来使微粒的更新速率适配寻优过程的各个阶段，并引入人工免疫(Artificial Immune, AI)思想形成免疫粒子群算法来拓展微粒的多样性，然后据此调整PID控制器的3个参数，最后利用此PID控制器调节水泵频率，使冷冻水回水温度稳定在设定值附近。结果表明，该策略能够很好地解决模型参数存在不确定摄动的问题，具有较强的鲁棒稳定性，节能效果显著。

1 人工免疫粒子群算法

1.1 粒子群算法惯性权重的确定

PSO算法是一种基于群体的全局优化方法，在1995年由Kennedy和Eberhart提出，源于对鸟群觅食行为的研究[10]。

假设在n维目标搜寻空间中初始化一个种群，种群中的微粒数为N，最大迭代次数为T，微粒的最大速度为Vmax，微粒i在该空间中的位置为Xi=(xi1,xi2,…,xin)，速度为Vi=(vi1,vi2,…,vin)，Vi∈[-Vmax,Vmax]。在每次迭代时，每个微粒先追踪迄今为止自身发现的最好位置Pi=(pi1,pi2,…,pin)与整个种群发现的最好位置Pg=(pg1,pg2,…,pgn)，再分别根据式(1)、(2)来调整自身的位置与速度，此间微粒的优劣程度根据其适应度函数值来判断。

Vi(t+1)=ωVi(t)+c1r1[Pi(t)-Xi(t)]+

c2r2[Pg(t)-Xi(t)]

(1)

Xi(t+1)=Xi(t)+Vi(t+1)

(2)

式(1)、(2)中，i=1,2,…,N,t=0,1,…,T；c1,c2∈[0,2]为加速常数；r1,r2为[0,1]的随机数，两者相互独立；ω为惯性权重。

PSO算法中惯性权重ω取值不合适易出现早熟现象，并且后期在全局最优值附近会发生振荡，导致结果误差较大。在迭代初期，ω应相对较大，增大粒子速度的更新步长，使粒子能较快地搜寻至可行解区域；在迭代后期，ω应相对较小，减小粒子速度的更新步长，使粒子能在可行解区域里作精细的局部搜索。故本文采用令ω随迭代数t增加呈指数形式单调减小的方法[11]，如式(3)所示:

(3)

其中：c>0为控制参数，其作用是控制惯性权重的收敛速度，取值范围通常为[6,8]；ωmax,ωmin分别为惯性权重的上下界。对式(3)进行求导并取绝对值可得到式(4)：

(4)

从式(4)可以发现ω(t)的减小量|Δω(t)|也呈指数形式单调减小。随着迭代数t增加，|Δω(t)|逐渐减小，当t增加至T时，|Δω(T)|=(ωmax-ωmin)×e-c×(c/T)，若忽略常系数ωmax-ωmin，对函数f(c)=e-c×(c/T)求导可得式(5):

(5)

综上所述，当t较小时，ω(t)较大，使粒子在初期保留历史速度的能力较大；随着t逐渐增大，ω(t)与|Δω(t)|均逐渐降低；当c>1且t增大至T时，|Δω(t)|趋于0，ω(t)趋于平稳。故本文所采用的惯性权重下降策略能较好地满足PSO算法在迭代过程中对惯性权重的要求。

1.2 AI算法改进PSO算法

上述改进PSO算法虽然具有较合适的更新速率，但仍然无法摆脱易收敛至局部最优值的问题。AI算法是一种模仿人体自然防御机制，从而解决数据处理、故障诊断、优化控制等问题的学习算法[12]。在PSO算法中引入人工免疫思想可以在寻优过程中保留高适应度微粒同时拓展其多样性，指导搜寻过程并抑制退化现象，使其更易收敛至全局最佳值，从而有效解决模型参数存在不确定摄动的问题。

利用AI算法改进PSO算法主要是引入人体免疫系统中的免疫记忆、自我调节、接种疫苗、免疫选择4种行为思想，模仿上述四种行为可作以下改进：

1)模仿免疫记忆行为来储存优质微粒，即将每次迭代产生的适应度值最高的微粒储存为记忆微粒。

2)模仿自我调节行为来取代不可用的微粒，检测每次迭代后的N个新微粒，若其中某个微粒的位置矢量X中某一维不在规定值域内，则用上一代记忆微粒替换。

在模仿接种疫苗与免疫选择行为之前，首先须要随机生成M个符合要求的微粒，然后按照亲和力强弱和浓度，在M+N个微粒中从新挑出N个新微粒。当微粒适应度值增大时，其亲和性愈强，故可取适应度函数的倒数来表示亲和性，即：

Ai=1/Ji

(6)

则由亲和力决定的选择概率为：

(7)

微粒的浓度可近似表示为：

(8)

则由浓度决定的选择概率为：

(9)

综上所述，某粒子被选中的概率为：

Hi=αHi1+(1-α)Hi2

(10)

其中：i=1,2,…,M+N，α∈[0,1]为权重系数。按照Hi大小对M+N个微粒排序，挑选出Hi较大的前N个微粒。

3)模仿接种疫苗行为改进PSO算法即从N个新微粒中挑选出某个微粒，再从上代记忆微粒的位置矢量X(t)中挑选出某维分量替换被挑选出的微粒对应维的值。

4)模仿免疫选择行为改进PSO算法即检验接种过疫苗后的微粒其位置矢量各维是否符合约束条件，若不符合则丢弃，不然求出适应度值。若求得的适应度值比接种之前小则丢弃，不然进行概率计算，即利用rand()生成一个值并与阈值p相比，若大于则用接种过疫苗的微粒替换父代微粒，不然丢弃。

2 AI-PSO算法优化PID控制器参数

常规PID控制率[13]如式(11)所示：

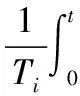
(11)

式(11)中，e(t)为控制偏差，e(t)=r(t)-y(t)；u(t)为控制输出；Kp为比例常数；Ti为积分时间常数；Td为微分时间常数。

利用上节所述AI-PSO算法优化PID控制器中Kp,Ti,Td三个参数，本质上是根据某一性能指标函数寻找最佳参数[14]，其控制原理如图1所示。

图1 AI-PSO算法优化PID控制器原理

对于PID控制器来说，目标函数即为衡量其性能要求的函数，通常分为调节品质型目标函数和误差积分型目标函数。为了避免振荡或调节时间过长，控制量过大，本文将时间乘绝对误差积分(Integrated Time Absolute Error, ITAE)函数[15]作为目标函数，即：

(12)

由于误差积分型目标函数值越小，系统精度越佳，故使得AI-PSO算法的适应度函数如式(13)所示：

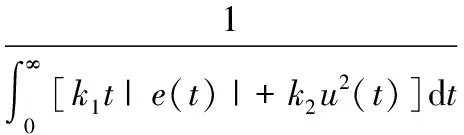
(13)

具体步骤如下：

步骤2 依据图1所示控制原理，利用式(13)来获取各个微粒的适应度值Ji, j(i=1,2,…,N;j=1,2,…,T-1)，并将此代中适应度值最佳的作为记忆微粒Bj纳入至知识库中；

步骤3 利用式(1)、(2)进行迭代，调整N个微粒的速度，并得到新一代各微粒的位置矢量Xi+1, j(i=1,2,…,N;j=1,2,…,T-1)；

步骤4 检验新一代各微粒的位置矢量，若某维数值不在规定的搜索域内，则以上一代的记忆微粒Bj代替；

步骤5 随机产生M个满足要求的微粒，并与步骤4中获取的N个微粒混合，利用式(13)来获取M+N个微粒的适应度值Ji+1, j(i=1,2,…,M+N;j=1,2,…,T-1)，再根据亲和力强弱与浓度大小所确定的挑选概率，即式(6)～(10)，从M+N个微粒中抽取出N个；

步骤6 针对步骤5中抽取出的N个微粒，随机挑出一个，并用记忆微粒Bj的位置矢量中某一维替换该微粒在对应维的分量；

步骤7 检验步骤6中替换后微粒的位置矢量各维是否在搜索域内，若不在则丢弃，再观察其与父代的适应度值，若比父代低则丢弃，最后进行概率对比，随机生成一个数值并与阈值p比较，若小于p则丢弃，否则用其替换父代微粒；

步骤8 将步骤6与7重复执行k次后，若已至最大迭代数或当前全局最优微粒符合要求，继续步骤9，不然转至步骤2；

步骤9 将步骤8中符合性能要求的全局最优微粒的位置矢量解码成PID控制器的3个参数。

3 建立控制对象数学模型

本文以中央空调冷冻水系统为控制对象，现实中该系统属于高阶系统，在建立模型时可以用带时滞的二阶惯性环节来近似描述[16]，其传递函数形式如式(15)所示。

(15)

其中：K为放大系数；T1,T2为惯性时间系数；τ为纯滞后时间参数。

利用南京工业大学智能建筑研究所内中央空调系统实验平台测量样本数据，该实验系统包括变频冷冻水泵、蒸发器、风机盘管、压缩机、冷却塔及其风机、冷却水泵、冷凝器，图2为其结构示意图。

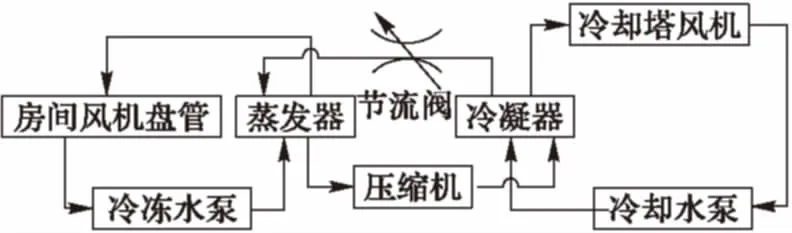
图2 中央空调系统结构

在夏季运行工况下共测得150对数据，每对数据包括采样时刻的冷冻水回水温度与水泵频率。图3、4为水泵频率与回水温度的变化曲线。

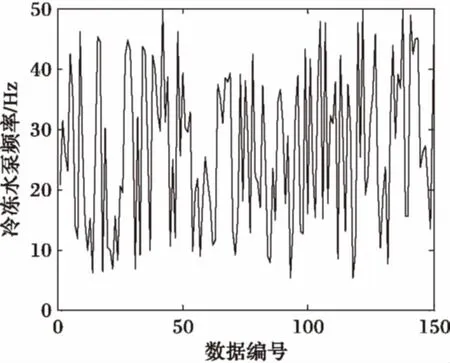
图3 水泵频率变化曲线

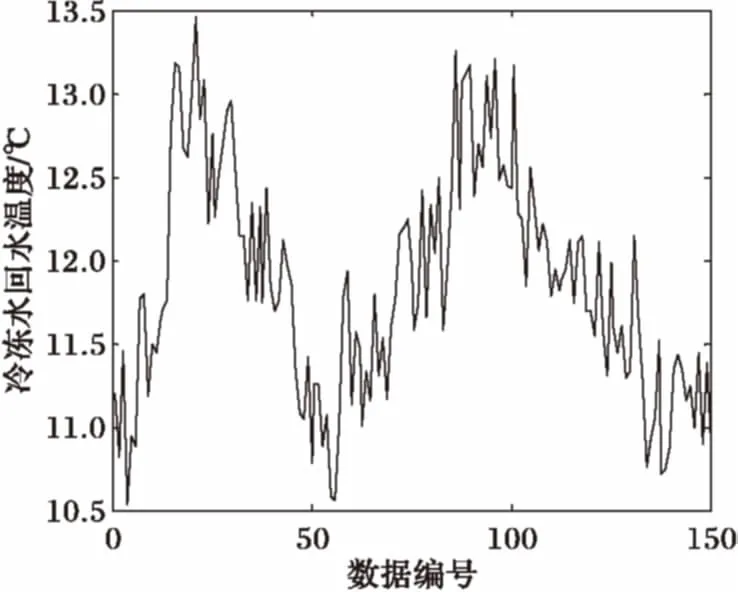
图4 冷冻水回水温度变化曲线

利用上述实测数据建立基于最小二乘法的自回归各态历经(AutoRegressive eXogenous, ARX)模型[17]，并找出拟合度最佳的曲线如图5所示。

经过数据处理与模型转换后，最终确定控制对象的传递函数如式(16)所示：

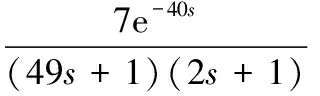
(16)

由于在实际过程中，该对象的模型参数存在不确定性而并非是固定不变的，因此为了评价系统的鲁棒稳定性，另取一条拟合度较佳曲线并获得传递函数如式(17)所示：

(17)

图5 水泵频率与回水温度拟合曲线

4 仿真与实验分析

变频冷冻水泵的送水温度恒为7°C，仿真时设定回水温度为12°C。利用Ziegler-Nichols整定法[18]计算出PID控制器的初始参数为Kp=0.3,Ti=60,Td=10。

首先，利用PSO算法优化PID控制器参数时，设定采样周期为0.01 s，Kp,Ti,Td的搜索域分别为[0,1],[0,100],[0,100]，最大迭代数为T=50，种群中粒子总数为N=20，每个粒子的维数为n=3，位置矢量为X=[Kp,Ti,Td]T，速度矢量的边界为Vmax=[1,1,1]T，c1=c2=2,r1=0.4,r2=0.6，惯性权重ω(t)如式(3)所示，其中ωmax=0.9,ωmin=0.1,c=7，适应度函数J中k1=0.002,k2=0.998；然后，利用AI-PSO算法优化时，再设定步骤5中M=10，筛选阈值p=0.5，亲和力与浓度权重系数α=0.3，接种疫苗与免疫选择反复次数k=5。

针对式(16)所示模型一分别采用AI-PSO与PSO算法优化后的PID控制仿真效果如图6所示。

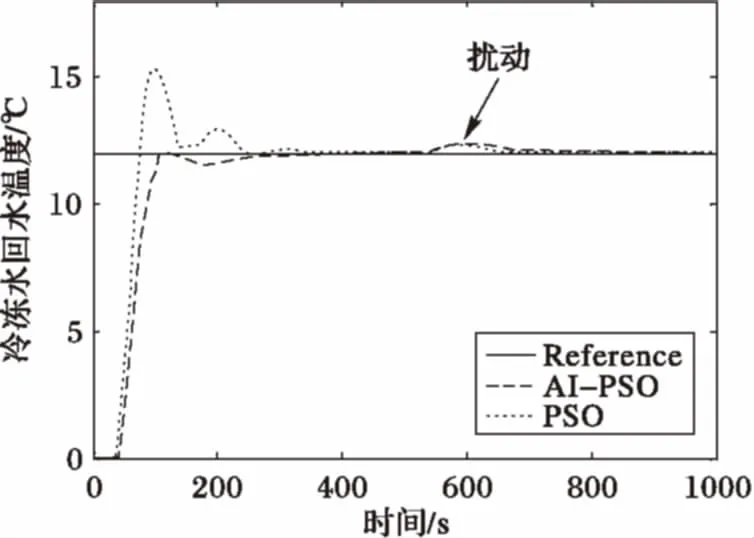
图6 模型一：两种算法优化PID控制阶跃响应曲线

当模型参数发生变化时，即当对象模型由模型一转变为式(17)所示模型二时，经两种算法优化后的PID控制器的控制仿真效果如图7所示。

针对模型一与模型二分别采用AI-PSO与PSO算法优化后的PID控制性能定量分析如表1所示。

图7 模型二：两种算法优化PID控制阶跃响应曲线

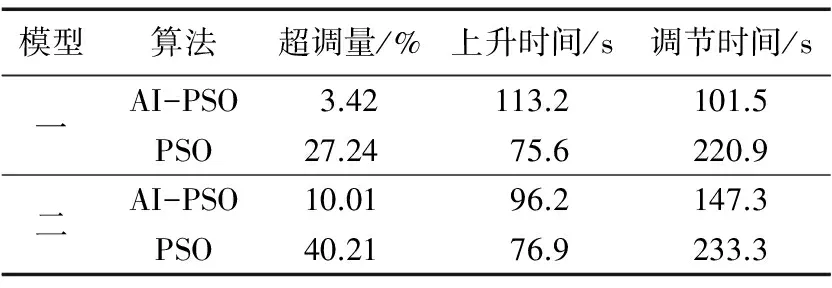
表1 不同模型两种算法优化PID控制性能比较

从仿真结果可见，经AI-PSO算法优化后的PID控制超调量更小，调节过程更短，尤其是当模型参数出现摄动时效果更为明显。但上升过程略长，且两者抗扰动能力与稳态误差没有较大差别。

之后将分别通过AI-PSO与PSO算法优化后的PID控制器参数输入至中央空调控制实验系统中进行性能测试。在稳定运行期间，由于人员进入以及室外气温上升引起热负荷扰动，从而导致模型参数出现不确定摄动，利用温度传感器实时测量回水温度，其变化曲线分别如图8、9所示。

图8 AI-PSO优化PID控制实测回水温度

图9 PSO优化PID控制实测回水温度

由图8、9可见，在实际应用过程中，对象模型参数出现不确定摄动造成的影响比仿真时更大，而采用通过AI-PSO算法优化参数的PID控制器能使回水温度更快更平稳地恢复至设定值附近，因此控制质量更佳。

室内实际负荷需求的变化使得变频器输出的水泵频率也跟着变化，从而降低水泵的能耗。在采用通过AI-PSO算法优化参数的PID控制器时，根据冷冻水流量的变化，利用电量采集模块得到冷冻水泵实际功率变化曲线如图10所示。

图10 冷冻水泵功率值变化曲线

由图10可知，实验期间采取变流量控制策略时水泵消耗电能为157.4 kWh。当采取定流量控制策略时，冷冻水流量需符合最大负荷需求，即始终保持为1 056.2 m3/h，而此时冷冻水泵的功率值约恒为14.67 kW/h，在实验过程中消耗电能为176.04 kWh。由此可见，采用冷冻水变流量优化控制能够使水泵降低10.59%的运行能耗。

5 结语

冷冻水回水温度优化控制能够根据室内实际负荷需求的变化自动调节冷冻水泵的频率，在部分负荷时能够减小冷冻水流量，与冷冻水定流量值相比能够更好地减小电能消耗。采用惯性权重呈指数形式下降的AI-PSO算法优化PID控制器的3个参数，使得回水温度能够维持在设定值附近，在保证室内实际负荷需求的前提下改进了控制质量，不仅延续了经典PID控制器结构简单的特性，还能在系统受到外部不确定因素摄动时使其快速趋于平稳。

References)

[1] 沈世平.某中央空调系统节能改造及能耗分析[D].重庆：重庆大学,2011:1-11.(SHEN S P. The energy-saving transformation and energy consumption analysis of a central air-conditioning system[D]. Chongqing:Chongqing University, 2011:1-11.)

[2] 洪丽娟,刘传聚.空调冷负荷时间频数及其应用[J].制冷与空调,2004,4(6):63-65.(HONG L J, LIU C J. Air-conditioning cooling load time frequency and its application [J]. Refrigeration and Air-conditioning, 2004, 4(6): 63-65.)

[3] 张少军，王亚慧，周渡海.变风量空调系统及控制技术[M].北京：中国电力出版社,2015:22-31.(ZHANG S J, WANG Y H, ZHOU D H. Variable Air Volume Air-Conditioning System and Its Control Technology [M]. Beijing: China Electric Power Press, 2015: 22-31.)

[4] 王伟,张晶涛.PID参数先进整定方法综述[J]. 自动化学报, 2000, 26(3): 347-355.(WANG W, ZHANG J T. A survey of advanced PID parameter tuning methods [J]. Acta Automatica Sinica, 2000, 26(3): 347-355.)

[5] SUN J M, ZHANG C D, ZHOU Z Y. Modeling and simulation of chilled water system for central air conditioning [J]. Applied Mechanics & Materials, 2012, 204/205/206/207/208: 4280-4285.

[6] SUN J M, ZHANG C D, ZHOU Z Y. Research of energy saving control for central air-conditioning based on adaptive fuzzy PID method [J]. Applied Mechanics & Materials, 2012, 204/205/206/207/208: 4286-4291.

[7] LI G. Fuzzy PID research on the temperature control system of central air conditioning based on genetic algorithms [J]. Information Technology Journal, 2013, 12(24): 839-847.

[8] ZHAO Y Q, ZHANG H L, ZHANG X F. Study on central air-conditioning system based on fuzzy prediction control [J]. Advanced Materials Research, 2014, 850/851: 644-647.

[9] 蒋红梅,李战明,唐伟强,等.变风量空调系统的优化控制研究[J]. 暖通空调, 2016,46(3):84-88.(JIANG H M, LI Z M, TANG W Q, et al. Optimal control on VAV air conditioning systems [J]. Heating Ventilating & Air Conditioning, 2016, 46(3): 84-88.)

[10] ABIDO M A. Optimal design of power system stabilizers using particle swarm optimization [J]. IEEE Transactions on Energy Conversion, 2002, 17(3): 406-413.

[11] LU J, HU H, BAI Y. Radial basis function neural network based on an improved exponential decreasing inertia weight-particle swarm optimization algorithm for AQI prediction [J]. Abstract and Applied Analysis, 2014, 2014(6): 1-9.

[12] 马佳.人工免疫算法理论与应用[M].沈阳：东北大学出版社,2014:9-16.(MA J. Theory and Application of Artificial Immune Algorithm [M]. Shenyang: Northeastern University Press, 2014: 9-16.)

[13] 刘金琨.先进PID控制MATLAB仿真[M].北京：电子工业出版社,2016:24-76.(LIU J K. Matlab Simulation of Advanced PID Control [M]. Beijing: Publishing House of Electronics Industry, 2016: 24-76.)

[14] 黄友锐，曲立国.PID控制器参数整定与实现[M].北京：科学出版社,2010:6-28.(HUANG Y R, QU L G. Parameter Tuning and Realization of PID Controller [M]. Beijing: Science Press, 2010: 6-28.)

[15] 韦根原,冯新强,韩璞.基于CQPSO算法的控制系统参数优化[J].系统仿真学报,2015,27(7):1570-1576.(WEI G Y, FENG X Q, HAN P. CQPSO algorithm based control system parameter optimization[J]. Journal of System Simulation, 2015, 27(7): 1570-1576.)

[16] 唐鑫.中央空调冷冻水系统一种智能控制方式的研究[D].重庆:重庆大学,2009:16-46.(TANG X. An intelligent control mode research for chilled water system of HVAC [D]. Chongqing: Chongqing University, 2009: 16-46.)

[17] LJUNG L. Black-box models from input-output measurements [C]// Proceedings of the 18th IEEE Instrumentation and Measurement Technology Conference. Piscataway, NJ: IEEE, 2001, 1: 138-146.

[18] 朱海锋.PID控制器参数自整定方法研究[D].广州：中山大学,2005:17-36.(ZHU H F. Research on parameter self-tuning method of PID controller [D]. Guangzhou: Sun Yat-Sen University, 2005: 17-36.)

Optimalcontrolofchilledwatersystemincentralair-conditioningbasedonartificialimmuneandparticleswarmoptimizationalgorithm

CHEN Dapeng1,2, ZHANG Jiugen1,2*, LIANG Xing1,2

(1.CollegeofElectricalEngineeringandControlScience,NanjingTechUniversity,NanjingJiangsu211800,China;2.InstituteofIntelligentBuilding,NanjingTechUniversity,NanjingJiangsu211800,China)

To reduce the running energy consumption of the central air conditioner and stabilize and control the return temperature of chilled water effectively, an optimal control method of return water temperature was proposed, and the actual load demand was judged according to the deviation between the measured value of return water temperature and the set value. Firstly, the inertia weight of Particle Swarm Optimization (PSO) algorithm was made decline exponentially which made updating speed of particles match each stage of optimization process. Then, aiming at uncertain disturbance of parameters of the model, the thoughts of Artificial Immune (AI) algorithm were introduced in Particle Swarm Optimization (PSO) algorithm to form AI-PSO algorithm which could expand the diversity of particles and enforce their ability to get rid of local optimum. Finally, three parameters of Proportional Integral Differential (PID) controller were optimized with AI-PSO algorithm, and through this controller, the frequency of chilled water pump was adjusted to make return water temperature steady near set value. The experimental results show that the proposed strategy can reduce operating frequency of chilled water pump more effectively while meeting indoor load demand, in addition, energy saving effect and control quality are much better.

return water temperature; Proportional Integral Differential (PID) controller; Particle Swarm Optimization (PSO) algorithm; Artificial Immune (AI) algorithm; energy conservation

2017- 03- 08;

2017- 04- 17。

陈大鹏(1992—)，男，江苏南通人，硕士研究生，主要研究方向：建筑智能化技术、绿色建筑仿真与设计、建模与智能控制； 张九根(1963—)，男，江苏南京人，副教授，博士，主要研究方向：建筑智能化技术、绿色建筑能耗监测与节能技术、计算机智能控制； 梁 星(1993—)，男，江苏常州人，硕士研究生，主要研究方向: 建筑设备系统建模与参数辨识。

1001- 9081(2017)09- 2717- 05

10.11772/j.issn.1001- 9081.2017.09.2717

TP302.7；TP391.9

A

CHENDapeng, born in 1992, M. S. candidate. His research interests include intelligent building technology, simulation and design of green buildings, modeling and intelligent control.

ZHANGJiugen, born in 1963, Ph. D., associate professor. His research interests include intelligent building technology, energy consumption monitoring and energy saving technology of green buildings, computer intelligent control.

LIANGXing, born in 1993, M. S. candidate. His research interests include modeling and parameter identification of building service system.