增强的单幅图像自学习超分辨方法

黄 凤，王晓明,2

(1.西华大学 计算机与软件工程学院，成都 610039； 2. 西华大学机器人研究中心，成都 610039)(*通信作者电子邮箱wxmwm@aliyun.com)

增强的单幅图像自学习超分辨方法

黄 凤1，王晓明1,2*

(1.西华大学 计算机与软件工程学院，成都 610039； 2. 西华大学机器人研究中心，成都 610039)(*通信作者电子邮箱wxmwm@aliyun.com)

针对图像超分辨率方法构建图像块的稀疏表示(SR)系数存在的主要问题，利用加权思想提出一种增强的单幅图像自学习超分辨方法。首先，通过自学习建立高低分辨率图像金字塔；然后，分别提取低分辨率图像的图像块特征和对应高分辨率图像块的中心像素，并给图像块中不同像素点赋予不同的权重，强调中心像素点在构建图像块稀疏系数时的作用；最后，结合SR理论和支持向量回归(SVR)技术建立超分辨率图像重建模型。实验结果表明，与单幅图像自学习超分辨率方法(SLSR)相比，所提方法的峰值信噪比(PSNR)平均提高了0.39 dB，无参考图像质量评价标准(BRISQUE)分数平均降低了9.7。从主观视角和客观数值证明了所提超分辨率方法更有效。

数字图像处理；单幅图像超分辨率；稀疏表达；支持向量回归；权重系数

0 引言

近年来，数字图像的超分辨率重建问题在图像科学和工程应用等领域得到了广泛的研究和发展。图像超分辨率是指从一幅低分辨率(Low Resolution, LR)图像或多幅LR图像中恢复出高分辨率(High Resolution, HR)图像[1]2-9，可分为单帧图像超分辨率和多帧图像超分辨率。单帧图像超分辨率是指只用一幅LR图像恢复HR图像；多帧图像超分辨率是指利用一系列带有亚像素位移的单帧LR图像恢复HR图像。本文研究的是单帧图像超分辨率。

总体上，单帧图像超分辨率的方法可分为基于插值、基于重建和基于学习的方法。图像插值的实质是通过结合基函数的加权和平移的离散和来表达一个连续的函数[2]。通常，基于插值的图像超分辨率方法具有结构简单、计算复杂度低等优点，但是，该类方法最容易模糊细节及其边缘，产生具有振铃和锯齿状的伪像。其中双三次插值(Bicubic Interpolation, BI)是插值法中最常见的方法。基于重建的方法主要包括频域法和空域法。频域法主要是基于傅里叶变换的平移和混叠特性生成HR图像，算法原理简单，但无法利用图像的先验信息，从而导致运动模糊和噪声对重建结果的影响较大。空域法则主要对图像的空间域进行处理，适用于包含运动、模糊和噪声的复杂观察模型。该方法在重建过程中利用图像的一些先验知识来约束重建模型，具有很强的空域先验约束能力，然而原理复杂，计算量大。

基于学习的超分辨率方法是近年超分辨率算法研究中的热点。与基于插值和重建方法不同，基于学习的方法借助机器学习，通过学习LR图像与HR图像之间的映射关系来预测LR图像中丢失的高频细节信息，从而实现HR图像的重建过程。该类方法的基本思想是：首先收集大量的HR图像及对应的LR图像，构造学习库，生成高低分辨率(HR/LR)图像学习模型，然后引入由学习模型获得的先验知识对待恢复的LR图像进行处理，得到图像的高频细节，最后获得超分辨率图像。大多数基于学习的超分辨率研究都是通过学习HR/LR图像之间的支持向量回归(Support Vector Regression, SVR)模型建立的HR图像[3-5]，这些文献整体布局分为训练和预测两大模块。在训练过程中，用SVR方法建立HR/LR图像间的非线性降质关系；在预测过程中，利用该关系得到LR图像丢失的高频信息，合成HR图像。基于SVR的超分辨率是图像超分辨率重建中一种典型的代表性算法。

近些年，随着压缩感知理论的发展，研究者们开始利用稀疏表示(Sparse Representation, SR)理论重建图像。稀疏表示模型开始被广泛应用于图像超分辨率中，如文献[6-13]。其基本思想：首先用稀疏表示模型训练HR/LR图像的字典，然后通过字典中很少量元素的线性组合描述LR图像，最后利用某种关系描述超分辨率图像。

2013年，Yang等[7]结合SVR和SR，提出了单幅图像自学习超分辨率方法(Self-Learning Super-Resolution approach for single image, SLSR)。该方法与大多数基于学习的方法不同，其不需要提前从外部图像库收集训练的HR/LR图像集。而是以输入图像为原型建立自学习的HR/LR图像金字塔；然后用SR理论建立图像块的稀疏系数，最后建立SVR模型实现图像的超分辨率。实验证明该方法具有很好的超分辨率效果。但是，该方法在图像块进行SR时，未考虑像素点之间的差异性和图像的连续性，认为LR图像块中每个像素点与相应HR图像块的中心像素点具有相同的映射关系，并且在自学习过程中，该方法未充分利用图像块大小构建尽可能多的不同尺度SVR模型。

针对上述超分辨率SR问题，本文提出一种增强的单幅图像自学习超分辨率方法。首先，通过图像退化模型对输入图像根据提取的图像块大小尽可能建立多尺度的自学习HR/LR图像金字塔；然后，提取图像特征，用权重思想对提取的图像块进行加权，不同的权重系数解释图像块中除中心点外其他点对中心点的贡献值大小；最后，结合SR理论、SVR原理，实现单幅图像的超分辨率重建。

1 相关工作

传统基于学习的超分辨率图像重建需要提前收集图像训练库，在很大程度上限制了超分辨率方法的应用，故本文采用自学习的超分辨方法。

自学习超分辨率方法的前提是以给定的HR图像为原型，通过退化模型建立超分辨率学习的HR/LR图像金字塔。通常图像的退化模型为：

Ilow=SBIhigh+n

(1)

其中:Ilow是LR图像，Ihigh是HR图像，S代表下采样过程，B代表模糊过程(高斯模糊、运动模糊等)，n代表噪声(高斯噪声、椒盐噪声等)。

1.1 稀疏表示理论

稀疏表示起源于信号研究，1993年Mallat[14]在基于小波分析中提出信号可以用一个超完备字典(Over-complete Dictionary,D)进行表示，随后稀疏表示理论被提出。稀疏表示是将原始信号x表达为字典元素的一个线性组合x=Dα，D是训练得到的字典，α为原始数据x在字典D上的表达，即稀疏系数。

设训练集{x1,x2,…,xm}，xi∈Rd，超完备字典D∈Rd×k，则{x1,x2,…,xm}的稀疏系数α∈Rk，解决问题：

(2)

1.2 支持向量回归原理

20世纪90年代中期，基于统计学习理论，Vapnik首次提出了支持向量机(Support Vector Machine, SVM)模型。其中SVR是支持向量在函数回归领域中的一个重要应用。

SVR[15]所寻求的是最优回归函数y=〈ω,x〉+b，ω∈Rd，b∈R，〈·,·〉表示在空间Rd的内积。最优回归函数对应于空间Rd×R上的一个超平面。设训练集{(x1,y1),(x2,y2),…,(xm,ym)}⊂Rd×R，为寻找非线性回归模型，首先将原始空间数据通过Φ映射到高维特征空间，其映射关系Φ:x|→Φ(x)；然后在高维特征空间中作近似线性回归，更新训练集{(Φ(x1),y1),(Φ(x2),y2),…,(Φ(xm),ym)}。

令K(xi,xj)=〈Φ(xi),Φ(xj)〉，则对应的原始优化问题为：

(3)

为解决上述优化问题，引进拉格朗日算子β、β*，采用Lagrange法把原始问题转化为如下的对偶优化问题求解：

(4)

最后得到SVR函数:

(5)

1.3 单幅图像自学习超分辨率方法

Yang等[7]提出的SLSR方法，首先对输入图像I通过退化模型建立三个不同尺度的HR/LR图像金字塔；然后对HR/LR图像分块、分类，学习不同图像块的字典，及稀疏表示系数。假设LR图像块中每一像素点对相应HR图像块的中心像素点具有相同影响值，及不同尺度的HR/LR图像之间具有相似的映射关系，最后借助SVR原理学习不同尺度的HR/LR图像的映射关系，由贝叶斯决策理论选取最优尺度的SVR模型，实现图像的超分辨率重建。文献[7]超分辨率方法原理的大致流程如图1所示。

图1 单幅图像自学习超分辨率方法

2 增强的单幅图像自学习超分辨率方法

传统基于SVR的超分辨率方法是构建LR图像块和HR图像块中心点的回归模型，其属于块对点的回归函数。该函数认为自变量LR图像块中每一点对因变量HR图像块中心点的影响作用一致。实质上，LR图像和HR图像为同一幅图像。本文鉴于回归函数的块对点的形式，和图像的连续性，在SVR建模时着重考虑以自变量LR图像块的中心为主导的某一小范围像素点对因变量HR图像块的中心像素点的影响，提出一种基于高斯核加权的SVR超分辨率方法。即在用SVR方法构建超分辨率学习模型时，对LR图像特征块进行加权，用权重系数解释图像块中每点对中心点的像素灰度值影响程度，最后用加权后的特征块和HR图像块中心像素点进行SVR建模。图2描述了利用SVR重建图像的传统超分辨率方法和本文方法的主要区别。

本文提出的方法：首先，对输入图像I建立LR图像和HR图像金字塔(HR/LR)；然后，学习LR图像的Sobel算子，对LR双三次插值放大的图像B及相应的HR图像分块、分类、特征提取，并对提取的特征块进行高斯核加权，得到加权后的图像特征数据集；最后，对特征数据集稀疏表示，用稀疏系数及HR图像块的中心像素灰度值建立非线性的SVR模型，选取误差最小的SVR模型预测HR图像块的中心像素，重建LR的超分辨率图像。

图2 传统超分辨率和本文超分辨率预测的主要区别

2.1 建立高低分辨率图像金字塔

大多数基于学习的超分辨率图像处理都是利用外部图像数据库，提前收集LR和HR图像，从而建立学习训练模型，恢复HR图像，如文献[3，5-6，13]；然而，基于外部图像库建立的超分辨率方法严格限制了其在生活中的实际应用。对此，本文提出一种增强的单幅图像自学习超分辨率方法。

设原始图像为I，I通过退化模型(1)建立多尺度不具有高频信息的降质图像集{LR-1,LR-2,LR-3,…}，同时对输入图像I用BI方法建立相对应带有高频信息的HR图像集{HR-1,HR-2,HR-3,…}，得到原始图像I的高低分辨率图像金字塔HR/LR。如图3底层所示。

图3 加权自学习SVR超分辨率主要框架

HR-i可以看成是训练图像LR-(i+1)的超分辨率图像。其中B序列图像是LR序列图像进行双三次插值上采样得到的，其大小和HR序列图像对应位置的相同。B序列图像中的方块表示建模选择的图像块，HR序列图像中的圆是方块对应HR图像块的中心像素点。

2.2 图像稀疏表示

2.2.1 特征提取

为提高超分辨率的效果，本文不直接对{LR-1,LR-2,LR-3,…}和{HR-1,HR-2,HR-3,…}提取图像特征，而是用Sobel算子对{LR-1,LR-2,LR-3,…}进行边缘检测，依次分类提取图像集{B-2,B-3,B-4,…}的特征块。

分类标准：若二值图像中点(u,v)的像素灰度值为0，则以点(u,v)为中心分割对应图像B-i得图像块矢量Xh和提取图像HR-i，点(u,v)处像素灰度值HR(u,v)。设h=HR(u,v)，得到具有高空间频率的训练集H={(Xh1,h1),(Xh2,h2),…}。若点(u,v)像素灰度值为255，分割图像B-i和HR-i，则得到具有低空间频率的图像块矢量Xl和块中心点灰度值HR(u,v)，构成低空间频率的训练集L={(Xl1,l1),(Xl2,l2),…}。

2.2.2 特征块高斯核加权及稀疏表示

设图像块大小为p×p，根据高斯核加权思想，对每一个图像块Xhi、Xlj进行高斯核加权：

(6)

其中:Xs,t是图像块在点(s,t)(s,t=1,2,…,p)的灰度值，r=(s,t)，rc=(p/2,p/2)或rc=((p+1)/2,(p+1)/2)(p∈N*)。参数σ是高斯滤波器宽度，控制加权的径向作用范围。通过调节σ，可在图像特征过分模糊与平滑图像中由于噪声和细纹理所引起的过多的欠平滑之间取得折中。

将加权后的图像块像素以行向量的形式表达，更新训练集H、L，如图4所示。则Xhi∈R1×p2、Xlj∈R1×p2，hi∈R、lj∈R。加权后的图像块的像素信息更多集中于图像块的中心区域，即HR图像块的中心附近。

图4 特征提取及加权

将Mairal 等[16-17]提出的矩阵分解和稀疏编码在线学习作为图像块的字典学习方法。通过字典学习得到稀疏系数，并进行计算，减少图像重建误差和提高运算速度。同时，考虑图像的纹理信息，本文对H、L中每个灰度值减去对应图像块的平均灰度值，然后用字典表示图像纹理信息，更新训练集H、L，对新的{Xhi}、{Xlj}特征块集合稀疏表示。

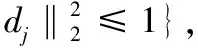
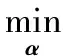
(7)

分别计算图像块{Xhi}、{Xlj}的稀疏系数{αhi}、{αlj}，λ为字典编码中稀疏约束参数。

2.3 基于SVR建立超分辨率模型

Δyhnorm=(Δh-Δhmin)/(Δhmax-Δhmin)

(8)

Δylnorm=(Δl-Δlmin)/(Δlmax-Δlmin)

(9)

图5 本文超分辨主要流程

由于在图像特征块加权时本文采用高斯核加权函数，其函数在除中心点一直为1外，其他点随σ不断增大，均不断增加到1，如图6所示。当σ足够大时，各加权系数均为1，此时本文提出的方法将接近SLSR方法[7]，亦可证明本文提出的方法有效性。同时，本文的方法可以看作是SLSR方法的一个推广。

图6 高斯核函数随σ的变化

3 实验设计与结果分析

本文的实验图像全部来源于南加州大学(University of Southern California, USC)图像数据库[19]。实验平台为处理器Intel Core i3- 4130 CPU @3.40 GHz的64位Windows 7旗舰版，Matlab R2015a。

3.1 图像评价标准及参数设计

为验证本文方法的有效性，本文在重建图像的质量评价上，首先用全参考(Full-Reference, FR)评价算法的峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)和结构相似性指数(Structural SIMilarity index, SSIM)作为评价指标，定义[1]93为：

(10)

(11)

其次考虑不依赖于原始真实图像的无参考(No-Reference, NR)图像质量评价算法。基于测试图像的普遍性和算法的建立方式，本文选择基于小波域两级框架的无参考图像质量评价模型(Blind Image Quality Index, BIQI)[20]和基于空域特征的无参考质量评价方法(Blind/Referenceless Image Spatial Quality Evaluator, BRISQUE)[21]作为超分辨率图像的质量评价指标。二者取值范围[0,100]，0表示图像质量最好，100表示图像质量最差。

在实验中，为模拟真实的退化图像过程，本文在实验的LR图像中均人为添加噪声。首先，对原始图像通过模型(1)高斯模糊；然后，以2的指数倍率进行下采样；最后，添加高斯白噪声得到含噪的测试LR图像。如此反复，建立HR/LR图像金字塔。

借鉴文献[7]稀疏表达参数、图像块大小的设置方式和实验图像大小，本文的参数设置如下：金字塔层数N1=5(所有测试图像大小为256×256)；多尺度模型N2=N1-1，图像块的大小p=5。训练集和测试集中数据的稀疏表示调用Mairal的SPAMS[22]工具箱，设置参数λ=0.025，字典原子数目k=100。SVR用LIBSVM[23]，其中核函数用径向基函数(Radial Basis Function, RBF)，参数gamma=1。数据集H的SVR参数c=4、ε=0.015 625；数据集L的参数c=2、ε=0.003 906 25，归一化误差△yhnorm、△ylnorm的SVR参数均设置为c=32、ε=0.007 812 5。这些SVR参数均由LIBSVM[23]工具箱的gridregression.py函数通过训练由本文方法处理后的Lena图(图7(h))数据集而得到。对于高斯核加权参数σ设计，将在实验结果中给出讨论和分析。

3.2 实验结果与分析

实验过程中，首先从图像库[19]中选取8幅不同类型、不同纹理的实验图像。若图像为彩色图像，则作相应灰度化处理；若图像大小不统一，则统一经过预处理得到256×256大小，得到测试图像(Girl、House、Tree、Jelly beans、Aerial、Clock、Resolution chart、Lena，如图7所示)。为检验本文方法的有效性，本文将提出的方法与双三次插值方法BI、稀疏表达的超分辨率方法SCSR[6]、基于稀疏编码网络的超分辨率方法SCN[13]、基于单幅图像自学习超分辨率方法SLSR[7](N2=3)(其中SCSR、SCN、SLSR相关代码均可在作者主页下载)、以及由文献[7]延伸出的单尺度SVR方法(N2=1)作比较，得到不同测试图像在多种超分辨率方法下的超分辨率重建结果。

由于本文的重点在图像块的加权上，故接下来讨论加权参数大小对图像超分辨率结果的影响。

图7 测试图像

3.2.1 权重系数对超分辨率重建的影响

表1 不同加权参数产生的超分辨率图像PSNR dB

从表1可以看出，同一幅图像在不同加权参数下，其超分辨率图像有不同的PSNR值，且PSNR值波动不大。观察表1，还可以发现，在实验的5种加权参数下，8幅测试图像虽然有不同的PSNR值，但大部分图像的最优PSNR值落在σ=3,5下。综合对比测试图像在不同加权参数下的平均PSNR值，选择实验的最优加权参数σ=5。故本文认为最优加权参数σ=p(p为提取图像块的大小)。

3.2.2 实验结果与分析

根据前面部分参数的设置及加权参数的讨论，本文设σ=5进行图像的超分辨率重建，并对多种方法重建后的超分辨率图像计算PSNR、SSIM得到表2，计算BIQI、BRISQUE得到表3。图8显示了部分图像的超分辨率结果的部分放大图像。

图8 各种方法实现超分辨率重建的部分放大图

为测试本文方法在视觉上的有效性，选择House、Aerial、Lena的超分辨率重建图像进行视觉上的对比。由表2知，本文方法对这3幅图像超分辨率重建的PSNR值与其他方法相比，明显最优。图8分别列出了House、Aerial、Lena原始HR图像及由BI、SCSR[6]、SCN[13]、单尺度SVR、SLSR[7]和本文方法产生的超分辨率图像的部分放大图像。通过观察局部放大图像可以看出，由BI方法重建的图像非常模糊，借助外部图像数据库训练模型建立超分辨率图像的SCSR[6]和SCN[13]方法的图像视觉效果最差，二者产生部分锯齿状斑块。分别观察图8(e)(f)(g)，虽然三者图像整体效果差不多，但是House图(g)房檐轮廓及房顶凸出部分相比其他二幅图像更清晰；Aerial图(g)街道梯子轮廓比其他图像轮廓清晰；Lena图(g)重建图像的眼睛、鼻子和嘴巴更接近原始HR图像，且相比其他三幅图像局部更清晰。最后，图9给出了其他5幅图像实验结果，观察图像同样可以得出本文提出的方法更有效。

比较观察表2中各个方法重建超分辨率图像的FR评价指标值，除Resolution chart图像外，通过本文方法重建的其他超分辨率图像的PSNR都比另外5种方法高；SSIM指标对比显示，虽然本文方法没有表现出全部最优，但大部分图像的SSIM都比另外5种方法高。其他5种方法中，由于SLSR[7]方法通过待测图像自身建立多尺度HR/LR图像金字塔，并用稀疏表达分块提取的图像块像素特征，所以，其重建的超分辨率图像FR评价指标更接近本文方法，单尺度SVR方法次之，BI方法紧随其后。相反，依赖于外部图像库提前训练数据集的SCSR[6]方法和SCN[13]方法的FR评价指标表现相对最差。分析其原因，主要本文测试图像大部分为人物，而SCSR[6]方法训练的外部图像库主要为植物类型图像，且训练样本太少，仅有69幅；SCN[13]方法训练样本仅有91幅。比较SSIM值，由本文方法重建的Aerial和Resolution chart图像均不是最高。Aerial通过SLSR[7]方法重建的超分辨率图像SSIM虽然最高，但其值和本文方法仅相差0.002 7。相反，Resolution chart通过BI方法重建的超分辨率图像SSIM比其他3种方法高得比较多，在结构相似性上更接近原始HR图像。分析其原因，主要是在多层金字塔建立过程中，由于数字图表类图像局部具有特征连续性，在多次下采样过程中丢失局部有效信息最多，其特征被忽略、模糊和边缘化，所以导致本文方法的重建效果差。

相比FR图像质量评价指标，比较观察表3，显然依赖于外部图像集的超分辨率方法在NR图像质量评价指标上占主导优势，而本文提出的方法无论是在BIQI指标还是BRISQUE指标上，其质量评价分数都相对高些，图像质量在小波域和空域特征上表现相对较差。但是，本文方法相对于另外3种方法表现较好。

表2 多种方法重建超分辨率图像的全参考指标PSNR和SSIM

表3 多种方法重建超分辨率图像的无参考指标BIQI和BRIQUE

表4给出了本文方法及对比方法重建超分辨率图像的平均时间。由于本文在对比SCN方法时，直接用的Wang等[13]训练好的级联网络模型，故本文仅给出了SCN方法的测试时间。比较每个方法的重建时间，考虑借用外部图像数据库训练模型的实际应用限制、对比FR图像质量评价指标值及NR图像质量评价指标值，得出：本文方法相对于其他5种超分辨率方法在实现上更方便，重建的图像质量更好。

表4 不同方法重建超分辨率图像的平均训练和测试时间对比

4 结语

本文针对单幅退化的LR图像，借鉴多尺度自学习模型和图像稀疏表示，考虑图像块的中心受其邻域灰度值的影响关系，对高维的图像数据建立了误差最小的SVR预测拟合模型，重点构建了影响稀疏字典和系数的加权特征块。因为图像的连续性，越靠近的像素点，关系越密切；越远离的像素点，关系越疏远，所以该方法最大的优势在于：对每个图像块的像素灰度值进行高斯核加权，用加权后的响应值代替原来图像块的像素值，进而与HR图像块中心像素点建立更有效的SVR模型。实验结果表明，本文设计的方法与其他基于学习的SVR和SR的超分辨率方法相比，其超分辨率重建图像视觉效果更好，同时表现出更好的超分辨率FR图像评价指标，特别是对人物图像。由于在图像退化过程中人为添加有噪声，故本文提出的方法也适用于图像去噪过程。而对于数字图表类图像，仍需提出更好的算法实现该类图像的超分辨率重建。未来将考虑改进特征的提取方式来提高对数字图表类图像的超分辨率重建，及降低重建图像的NR图像评价指标值。

图9 各种方法重建的超分辨率图像

References)

[1] 杨欣.图像超分辨率技术原理及应用[M].北京：国防工业出版社,2013:2-9,93.(YANG X. Image Super Resolution Technology Principle and Application [M]. Beijing: National Defense Industry Press, 2013: 2-9,93.)

[2] 赵伟.基于多幅低分辨率图像的超分辨率图像重建[D].南京: 东南大学,2011：12-17. (ZHAO W. Super-resolution image reconstruction based on multiple low resolution images [D]. Nanjing: Southeast University, 2011: 12-17.)

[3] 王宇,吴炜,严斌宇,等.基于SVR的人脸图像超分辨率复原算法[J].四川大学学报(自然科学版),2013,50(4):728-736.(WANG Y, WU W, YAN B Y, et al. Face hallucination based on SVR [J].Journal of Sichuan University (Natural Science Edition), 2013, 50(4): 728-736.)

[4] XU J, DENG C, GAO X, et al. Image super-resolution using multi-layer support vector regression [C]// Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway, NJ: IEEE, 2014: 5799-5803.

[5] AN L, BHANU B. Improved image super-resolution by support vector regression [C]// Proceedings of the 2011 International Joint Conference on Neural Networks. Piscataway, NJ: IEEE, 2011: 696-700.

[6] YANG J, WRIGHT J, HUANG T S, et al. Image super-resolution via sparse representation [J]. IEEE Transactions on Image Processing, 2010, 19(11): 2861-2873.

[7] YANG M C, WANG Y C F. A self-learning approach to single image super-resolution [J]. IEEE Transactions on Multimedia, 2013, 15(3):498-508.

[8] YANG M C, CHU C T, WANG Y C F. Learning sparse image representation with support vector regression for single-image super-resolution [C]// Proceedings of the 2010 17th IEEE International Conference on Image Processing. Piscataway, NJ: IEEE, 2010: 1973-1976.

[9] 范九伦,史香晔,徐健,等.多级字典学习的图像超分辨率算法[J].西安邮电大学学报,2016,21(3):32-37.(FAN J L, SHI X Y, XU J, et al. Image super-resolution algorithm based on multi-level dictionaries learning [J]. Journal of Xi’an University of Posts and Telecommunications, 2016, 21(3): 32-37.)

[10] 邱大伟,刘彦隆.改进的稀疏表示图像超分辨率复原算法[J].电视技术，2016,40(1):135-140. (QIU D W, LIU Y L. Improved image super-resolution via sparse representation [J]. Video Engineering, 2016, 40(1): 135-140.)

[11] 李欣,崔子冠,孙林慧,等.基于局部回归模型的图像超分辨率重建[J].计算机应用,2016,36(6):1654-1658. (LI X, CUI Z G, SUN L H, et al. Image super-resolution reconstruction based on local regression model [J]. Journal of Computer Applications, 2016, 36(6): 1654-1658.)

[12] 王宏,卢芳芳,李建武.结合支持向量回归和图像自相似的单幅图像超分辨率算法[J].中国图象图形学报,2016,21(8):986-992.(WANG H, LU F F, LI J W. Single image super-resolution via support vector regression and image self-similarity [J]. Journal of Image and Graphics, 2016, 21(8): 986-992.)[13] WANG Z, LIU D, YANG J, et al. Deep networks for image super-resolution with sparse prior [EB/OL]. [2016- 12- 07]. http://pdfs.semanticscholar.org/27fc/88ebb3e325a062a6ff48a7a76611af1ecd5a.pdf.

[14] MALLAT S. A wavelet tour of signal processing: the sparse way [EB/OL]. [2016- 12- 07]. http://www.gbv.de/dms/ilmenau/toc/579284751.PDF.

[15] BASAK D, PAL S, PATRANABIS D C. Support vector regression [J]. Neural Information Processing Letters and Reviews, 2007, 11(10): 203-224.

[16] MAIRAL J, BACH F, PONCE J, et al. Online learning for matrix factorization and sparse coding [J]. Journal of Machine Learning Research, 2010, 11(1): 19-60.

[17] MAIRAL J, BACH F, PONCE J, et al. Online dictionary learning for sparse coding [C]// Proceedings of the 26th Annual International Conference on Machine Learning. New York: ACM, 2009: 689-696.

[18] EFRON B, HASTIE T, JOHNSTONE I, et al. Least angle regression (with discussion) [EB/OL]. [2017- 01- 06]. https://web.stanford.edu/～hastie/Papers/LARS/LeastAngle_2002.pdf.

[19] University of Southern California. The USC-SIPI image database [DB/OL]. [2016- 08- 20]. http://sipi.usc.edu/database/.

[20] MOORTHY A K, BOVIK A C. A two-step framework for constructing blind image quality indices [J]. IEEE Signal Processing Letters, 2010, 17(5): 513-516.

[21] MITTAL A, MOORTHY A K, BOVIK A C. No-reference image quality assessment in the spatial domain [J]. IEEE Transactions on Image Processing, 2012, 21(12): 4695-4708.

[22] MAIRAL J. SPAMS: a sparse modeling software, v2.5 [EB/OL]. [2016- 10- 23]. http://spams-devel.gforge.inria.fr/downloads.html.

[23] CHANG C, LIN C J. LIBSVM: a library for support vector machines [EB/OL]. [2016- 10- 18]. http://www.csie.ntu.edu.tw/～cjlin/libsvm.

Enhancedself-learningsuper-resolutionapproachforsingleimage

HUANG Feng1, WANG Xiaoming1,2*

(1.SchoolofComputerandSoftwareEngineering,XihuaUniversity,ChengduSichuan610039,China;2.RoboticsResearchCenterofXihuaUniversity,ChengduSichuan610039,China)

Aiming at the main problem of the Sparse Representation (SR) coefficients of the image blocks in image super-resolution method, an enhanced self-learning super-resolution approach for single image was proposed by using the weighting idea. Firstly, the pyramid of high and low resolution images was established by self-learning. Then, the image block feature of low-resolution images and the central pixels of the corresponding high-resolution image blocks were extracted respectively. The role of the center pixel in constructing the image block sparse coefficient was emphasized by giving different weights of different pixels in the image blocks. Finally, the combination of SR theory and Support Vector Regression (SVR) technique was used to build the super-resolution image reconstruction model. The experimental results show that compared with the Self-Learning Super-Resolution method for single image (SLSR), the Peak Signal-to-Noise Ratio (PSNR) of the proposed method is increased by an average of 0.39 dB, the BRISQUE (Blind/Reference-less Image Spatial Quality Evaluator) score of no-reference image quality evaluation criteria is reduced by an average of 9.7. From the subjective perspective and objective values, it is proved that the proposed super resolution method is more effective.

digital image processing; single image super-resolution; Sparse Representation (SR); Support Vector Regression (SVR); weight coefficient

2017- 03- 30;

2017- 06- 07。

国家自然科学基金资助项目(61532009)；教育部春晖计划项目(Z2015102)；四川省教育厅自然科学重点项目(11ZA004)。

黄凤(1993—)，女，四川南部人，硕士研究生，主要研究方向：图像超分辨率重建； 王晓明(1977—)，男，四川简阳人，副教授，博士，主要研究方向：模式识别、机器学习、图像处理、计算机视觉。

1001- 9081(2017)09- 2636- 07

10.11772/j.issn.1001- 9081.2017.09.2636

TP391.41

A

This work is partially supported by the National Natural Science Foundation of China (61532009), the Chunhui Program of Ministry of Education (Z2015102), the Key Scientific Research Project of Sichuan Provincial Department of Education (11ZA004).

HUANGFeng, born in 1993, M. S. candidate. Her research interests include image super-resolution reconstruction.

WANGXiaoming, born in 1977, Ph. D., associate professor. His research interests include pattern recognition, machine learning, image processing, computer vision.