基于压缩感知的多小区MASSIVE MIMO信道估计

刘紫燕，唐 虎，刘世美

(贵州大学 大数据与信息工程学院，贵阳 550025)(*通信作者电子邮箱leizy@sina.com)

基于压缩感知的多小区MASSIVE MIMO信道估计

刘紫燕*，唐 虎，刘世美

(贵州大学 大数据与信息工程学院，贵阳 550025)(*通信作者电子邮箱leizy@sina.com)

针对多小区多用户大规模多输入多输出(MASSIVE MIMO)系统信道估计在低信噪比情况下估计精度较差的问题，提出了一种基于群智能搜索的果蝇分段正交匹配追踪(FF-StOMP)压缩感知算法。该算法在分段正交匹配追踪(StOMP)求解不同阈值下的信道矩阵参数与归一化最小均方误差的基础上，采用果蝇优化算法动态搜索出最小归一化均方误差与其对应的阈值，达到自适应参数设定的目的。仿真结果表明，与StOMP算法相比，信噪比在0～10 dB情况下，所提出的FF-StOMP算法信道估计性能能够提升0.5～1 dB；信噪比在11～20 dB时,信道估计性能能够提升0.2～0.3 dB。当小区用户数发生变化时，所提出的算法能实现自适应信道估计，能够有效提升MASSIVE MIMO系统低信噪比情况下的信道估计精度。

大规模多输入多输出技术；多小区信道估计；自适应压缩感知；分段正交匹配追踪算法

0 引言

大规模多输入多输出(MASSIVE Multi-Input Multi-Output, MASSIVE MIMO)技术作为未来5G无线通信的关键技术之一，由于其频谱效率高、鲁棒性高等优点而受到广泛关注[1]。大数定理指出，当收发两端安装的天线较大时，相互独立的信道矢量之间表现为大的随机矢量，并且在信道环境处于理想时呈现为正交性。这一特性带来的优势就是当接收端得到准确信道状态信息(Channel State Information, CSI)时，采用简单的恢复算法就能排除其他用户的干扰，有效地提高信道的频谱利用率[2]。因此，准确获得CSI对于MASSIVE MIMO系统有着重要的作用。

常见的信道估计算法中，非盲信道估计方法因其算法的复杂度低而被广泛运用，其原理是在发送端发送特定的训练序列来进行信道估计，在用户数据中插入训练序列，用户数据与插入的训练序列组成发射端的数据帧结构。接收端采用相关算法进行信道估计，用户的数据则由估计的信道参数进行恢复。传统的信道估计算法有最小二乘(Least Square, LS)估计算法，最小均方误差估计(Minimum Mean Square Error, MMSE)算法等。这些算法对训练序列的要求较高，需要正交导频序列，才能获得较好的估计效果，因此增加了导频序列的开销，而且实现难度较大。

近几年，基于压缩感知的稀疏信道估计方法[3-6]陆续被提出。压缩感知理论是由Donoho和Candes提出的一种充分利用信号稀疏性的信号采样理论。该理论突破了传统的Nyquist定理，在对数据进行采集时同时对数据进行了压缩，实现了采集压缩于一体，克服了采样数据量大、采样时间长及数据存储空间大的问题。“稀疏性”是压缩感知应用的前提，由于信道矩阵在某个域内呈现稀疏特性，采用压缩感知重构算法能够以大概率恢复出信道矩阵参数。目前基于压缩感知算法的信道估计一般采用计算复杂度低且易实现的正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法[7]，在信噪比较高的环境下，可以获得比较好的MMSE估计性能，但是在信噪比较低的环境下，估计性能较差。文献[8]中提出了一种粒子群优化算法对分段正交匹配追踪(Stagewise Orthogonal Matching Pursuit, StOMP)算法阈值及迭代次数进行训练，从而搜索出最佳的阈值以及迭代次数，但是针对不同的场景，需要重新训练参数。文献[9]研究了时分双工(Time Division Duplexing, TDD)系统中多用户的信道估计问题，采用基于压缩感知的低秩矩阵逼近算法，但是此算法仅限于有限散射模型的物理信道，局限性较大。为了有效估计MASSIVE MIMO信道矩阵，文献[10]提出了一种基于压缩感知的信道估计方案，但这个方案仅仅考虑了频分双工(Frequency Division Duplexing, FDD)系统模型。

针对OMP算法在低信噪比情况下的信道估计性能较差，以及在不同情况下StOMP算法参数需要多次训练的问题。本文是对StOMP算法参数处理，采用果蝇算法对StOMP算法中的阈值参数进行动态搜索，实现了阈值参数自适应。

1 MAASIVE MIMO系统稀疏信道模型

1.1 压缩感知基本理论

压缩感知测量形式如下：

y=Φx

(1)

其中：x∈RN×1是未知的稀疏信号(‖x‖0≤N)，Φ∈RM×N是测量矩阵(M≤N)，y∈RM×1是测量信号。稀疏信号x在

M≥K·lgN

(2)

的情况下可以通过y和Φ重构出来，其中K是信号的稀疏度(即表示信号x中非零元素的个数)。重构数学模型如下：

(3)

约束条件：Φx=y

压缩感知中“K稀疏”即对于长度为N的向量来说，它的N个元素值中只有K个是非零的(其中K≪N)，称这个向量是K稀疏的或者严格K稀疏；实际中要做到严格K稀疏十分困难，一般只要除了这K个值外，其他的值很小，就可以视为该向量是“稀疏”的，如果信号是稀疏的，则可采用压缩感知重构算法恢复出原信号。

1.2 MASSIVE MIMO系统稀疏信道模型

考虑如图1所示的多小区多用户MASSIVE MIMO系统模型。每个小区配置一个基站，基站使用“中心激励”的方式，配置了M根线性均匀排列(Uniform Linear Array, ULA)的天线，同时服务K个单天线用户(其中M≥K)，系统采用TDD的工作方式。基站端利用接收到的训练序列信号估计上行信道矩阵参数，而下行信道矩阵参数的估计则利用TDD系统的信道互易性获得。

假设G1l∈RM×K表示第l个小区内K个用户到第一个小区基站的无线传播信道矩阵参数，G1L∈RM×K表示第L个小区内K个用户到第一个小区基站的无线传播信道矩阵参数。在该通信系统模型中，第l个小区为目标小区，基站接收到的信号yl∈RM×1表示为：

(4)

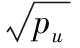
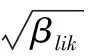
(5)

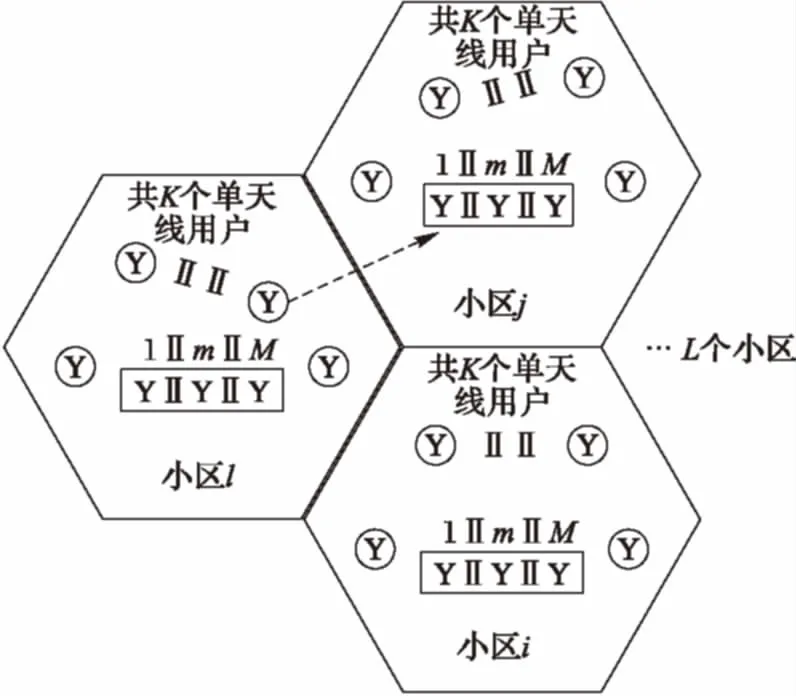
图1 多小区MASSIVE MIMO系统模型

图2 合成信道矩阵近似“稀疏”矩阵

1.3 MASSIVE MIMO信道估计模型

假设小区用户发送的训练序列长度为J，发送训练序列为Xi∈RK×J。将式(4)表示为矩阵形式：

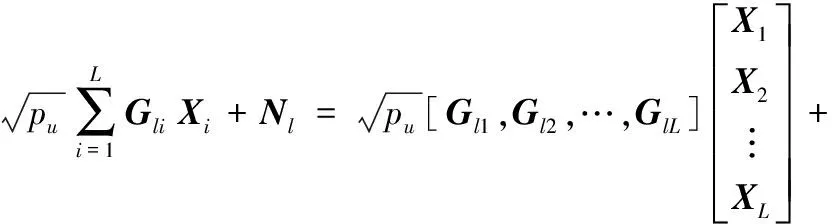
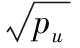
(6)

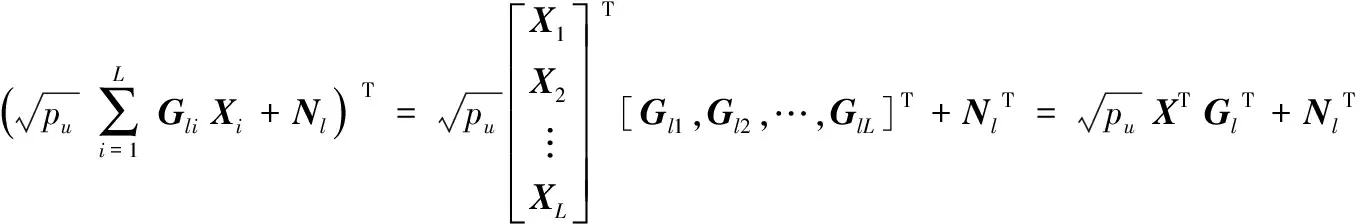
(7)

对比式(1)与式(7)，其基本形式一致，即式(7)可通过压缩感知恢复算法重构出原始信号。

2 基于FF-StOMP算法的信道估计

2.1 St_OMP算法

常见的压缩感知重构算法包括两类：一类是凸松弛算法，另一类是贪婪算法。凸松弛算法是通过在一定条件下将非凸的l0范数优化问题转化为凸的l1范数优化问题求解。凸松弛算法所需的观测数目少，但是计算复杂度很高，算法收敛慢[12]；贪婪算法重构质量略差于凸松弛算法，但原理简单、实现容易、运行速度快，由于其计算复杂度小，故在实际应用广泛。

典型的贪婪重构算法有正交匹配追踪(OMP)算法、分段正交匹配追踪(StOMP)算法[13]，压缩采样匹配追踪(Compressive Sampling Matching Pursuit, CoSaMP)算法[14]，子空间追踪(Subspace Pursuit, SP)算法等[15]。

分段正交匹配追踪(StOMP)算法是基于OMP改进而来的一种贪心算法，该算法在迭代选择原子时，每次选择多个原子，选择的规则是通过一个阈值ts来决定，而且迭代次数S也是需要手动设置。ts取值过大会降低算法的效率，过小则会降低重构精度，合理设置阈值参数十分重要。

与OMP算法相比，StOMP算法执行效率高；与SP算法、CoSaMP算法相比，区别是CoSaMP、SP算法在迭代过程中选择的是与信号内积最大的2K或K个原子，而StOMP则是通过门限阈值来选择原子。此算法的输入参数中无信号的稀疏度K，因此相比OMP算法、SP及CoSaMP算法有独到的优势。StOMP算法步骤如下：

步骤1 初始化：r0=y；I=∅；t← 1；

步骤2 计算不同阈值情况下的u=abs[XTrt-1](即计算J={rt-1,aj>ts·σt,1≤j≤N})，选择u中大于门限ts·σt的值；

步骤3 更新索引集I=I∪{J}；

步骤4 更新解与残差：

步骤5 若t=n，则停止迭代，否则，转到步骤1。

2.2 FF-StOMP算法信道估计

由于在实际场景中，用户数是随机变化的，即信号的稀疏度这一信息是不确定的，OMP算法和CoSaMP算法不可行。根据前文所述，StOMP算法不需要知道信号的稀疏度，但是在重构信号的构成中需要手动设置迭代次数S和阈值参数ts，而当用户数(即信号的稀疏度)发生改变的时候，经验设置的阈值参数不可靠。针对此问题，本文结合果蝇优化算法对指定范围内的阈值参数，提出一种基于稀疏度自适应果蝇分段正交匹配追踪(Fruit Fly Stagewise Orthogonal Matching Pursuit, FF-StOMP)算法,流程如图3所示。

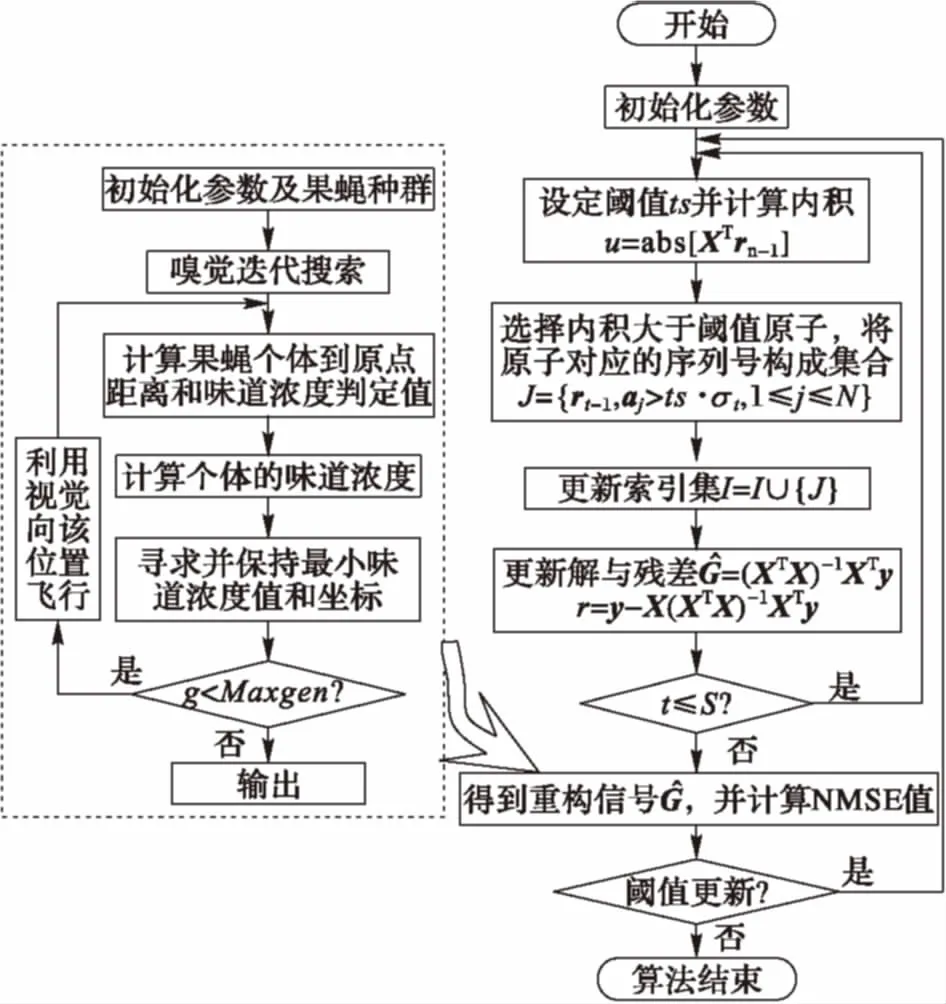
图3 FF-StOMP算法流程

果蝇优化算法(Fruit fly Optimization Algorithm, FOA)是一种模拟通过果蝇觅食行为推演出寻求全局优化的新方法。该算法实现容易，收敛速度快，参数设置简单，是一种高效寻优算法。在果蝇算法中，优化问题均可以视为一只果蝇，所有的果蝇都有一个被优化函数决定的“浓度判定函数”(即适应度函数)。每只果蝇还有一个“浓度”来判定其搜索食物的飞行方向和距离。果蝇算法首先随机初始化一群果蝇的位置，然后通过迭代去寻找最优解，每次迭代，果蝇通过“浓度判定值”来更新自己，直到寻求到最优解。

FF-StOMP算法思想是采用果蝇优化算法对某一范围内的阈值参数搜索，通过迭代寻找到稀疏信道估计性能最佳时所对应的阈值参数，并记录此时的最佳阈值参数及估计误差。

本文采用归一化均方误差(Normalized Mean Square Error,NMSE)[16]算法来评价稀疏信道估计的性能，NMSE算法定义为：

(8)

(9)

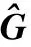
(10)

约束条件：

u=abs[XTrt-1]≥ts·σt

其中:u是当前阈值下选择出的原子内积，σt是残差的2范数倍数，其倍数由训练序列矩阵的方差决定，此处的训练序列采用高斯随机序列，方差为1/M，r为残差，ts为设置的阈值参数。

3 仿真结果及分析

为了验证本文所提出的FF-StOMP算法对MASSIVE MIMO系统信道估计性能的提升，下面在Matlab 2014b平台上进行仿真。仿真系统的小区半径为1 000 m的正六边形，用户随机分配在距离基站100 m以外的范围，小区个数为5个，每个小区用户数为5个，发送的训练序列长度为40，发送的训练序列总发射功率为0.1 mW。考虑到计算量较大，每个小区用户数变化时，用户数目设置在3～14共11组。FF-StOMP算法迭代次数根据经验设置为10[7]，阈值搜索区间为[2.0,3.0][16]，搜索的步进长度为0.1。FF-StOMP算法算法参数设置如表1所示。

表1 FF-StOMP算法参数设置

图4是采用FF-StOMP算法在求解最小NMSE时，自适应搜索出的最佳阈值ts。

从图4可以看出，在每个小区内，当用户数K发生改变时，FF-StOMP算法搜索出的最佳阈值也会自适应变化。这是因为StOMP算法中阈值参数需要凭经验设置，但是针对不同情况，经验设置可靠性不高，但是FF-StOMP算法能够根据果蝇觅食特性，自适应选择最佳阈值参数，以达到最佳估计效果。

本文仿真单个小区用户数为5，训练序列长度为40。为了验证阈值参数对系统性能的影响，选择常见阈值，以ts=2.4为例[15]，进行仿真分析。

图5为3种算法的估计性能比较。由图5可以看出，在低信噪比情况下，NMSE取值相同时，即系统具有相同的估计性能，StOMP(阈值ts=2.4)算法比OMP算法估计性能平均提高约2 dB，采用FF-StOMP算法获得的估计性能，在信噪比为0～10 dB的情况下，比StOMP算法估计性能提高0.8～1 dB；在11～20 dB情况下FF-StOMP算法信道估计性能能够提高0.2～0.3 dB。是因为在FF-StOMP算法能够自适应调整阈值参数，选择最佳的阈值，可以从图4看出，此时的最佳阈值为ts=2.0。

图4 每个小区不同用户数的最佳阈值

图5 每个小区用户数为5时估计性能比较

图6为单个小区用户数为8，训练序列长度为40时，3种算法的估计性能比较。由图6与图5比较可以看出，估计性能误差有所增大，因为随着每个小区用户数增加，信道矩阵维度增加，导致计算复杂度增加，所以估计性能有所降低。图6中，在信噪比较低时，NMSE取值相同时，即系统具有相同的估计性能，手动设置阈值算法比OMP算法估计性能平均提高约2 dB。在信噪比为0～10 dB的情况下，采用FF-StOMP算法获得的估计性能，比StOMP算法(阈值ts=2.4)有0.5～0.8 dB提升；在11～20 dB情况下FF-StOMP算法信道估计性能能够提高0.2～0.3 dB。由图4可知，此时搜索的最佳阈值为ts=2.1。结合图5与图6，可以看出本文所提出的FF-StOMP算法在单个小区用户数发生改变时，依然可以自适应搜索出最佳阈值，获得较好的估计性能。

图6 每个小区用户数为8时估计性能比较

图7为每个小区用户数为6时，3种算法的估计性能比较。由图1可以得出，此时FF-StOMP算法搜索最佳阈值ts=2.4，由图7可以看出，人工设置阈值算法与FF-StOMP算法估计性能大致相近。

图8为小区内不同用户数的估计性能比较。由图8可以看出，随着小区内用户数目的改变，本文提出的FF-StOMP算法能够始终获得较好的估计性能。由此可以看出，FF-StOMP算法能够自适应调整阈值参数，获得较好的估计性能。

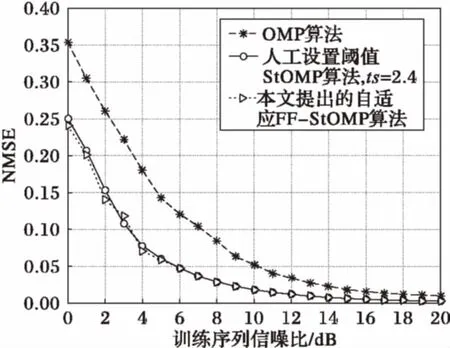
图7 每个小区用户数为6时估计性能比较

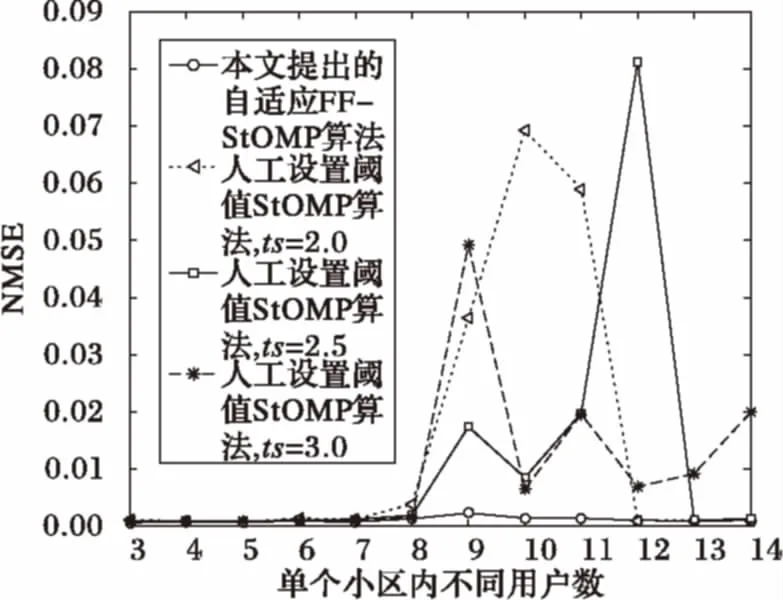
图8 每个小区内不同用户数估计性能

4 结语

本文研究了多小区多用户MASSIVE MIMO系统中的信道估计问题，提出了一种自适应压缩感知的FF-StOMP算法。考虑TDD系统的信道特性，构建了多小区多用户的联合信道矩阵近似“稀疏”模型。当小区内的用户数发生改变时，StOMP算法需凭人工经验设置阈值，故结合果蝇算法对其阈值进行动态搜索，达到自适应信道估计的目的。理论分析与仿真表明，所提出的FF-StOMP算法在小区用户数发生改变时能够自适应搜索最佳阈值，达到较好的估计性能。本文仅仅只是对阈值进行动态搜索，之后可考虑对迭代次数进行动态搜索，研究其对信道估计性能影响。

References)

[1] HOYDIS J, BRINK S T, DEBBAH M. Massive MIMO in the UL/DL of cellular networks: how many antennas do we need? [J]. IEEE Journal on Selected Areas in Communications, 2013, 31(2): 160-171.

[2] 王玉鹏.基于压缩感知的MASSIVE MIMO系统中信道估计算法的研究[D].成都:电子科技大学,2015:1-2.(WANG Y P. Channel estimation of MASSIVE MIMO [D]. Chengdu: University of Electronic Science and Technology of China, 2015: 1-2.)

[3] NAN Y, ZHANG L, SUN X. Efficient downlink channel estimation scheme based on block-structured compressive sensing for TDD massive MU-MIMO systems [J]. IEEE Wireless Communications Letters, 2015, 4(4): 345-348.

[4] 谢建超.Massive MIMO通信系统中信道估计技术研究[D].南京:南京邮电大学,2016:44-51.(XIE J C. Research on channel estimation technology for massive MIMO communication system [D]. Nanjing: Nanjing University of Posts and Telecommunications, 2016: 44-51.)

[5] QI C, HUANG Y, JIN S, et al. Sparse channel estimation based on compressed sensing for massive MIMO systems [C]// Proceedings of the 2015 IEEE International Conference on Communications. Piscataway, NJ: IEEE, 2015: 4558-4563.

[6] LEE J, GIL G T, LEE Y H. Exploiting spatial sparsity for estimating channels of hybrid MIMO systems in millimeter wave communications [C]// Proceedings of the 2014 IEEE Global Communications Conference. Piscataway, NJ: IEEE, 2015: 3326-3331.

[7] TAN G, HERFET T. A framework of analyzing OMP-based channel estimations in mobile OFDM systems [J]. IEEE Wireless Communications Letters, 2016, 5(4): 408-411.

[8] 陈艳良,战荫伟.贪婪重构算法StOMP及其改进[J].计算机应用与软件,2016,33(4):258-261.(CHEN Y L, ZHAN Y W. Greedy reconstruction algorithm StOMP and its improvement [J]. Computer Applications and Software, 2016, 33(4): 258-261.)

[9] NGUYEN S L H, GHRAYEB A. Compressive sensing-based channel estimation for massive multiuser MIMO systems [C]// Proceedings of the 2013 IEEE Wireless Communications and Networking Conference. Piscataway, NJ: 2013: 2890-2895.

[10] DAI L, GAO Z, WANG Z, et al. Spectrum-efficient superimposed pilot design based on structured compressive sensing for downlink large-scale MIMO systems [C]// Proceedings of the 2014 XXXIth URSI General Assembly and Scientific Symposium. Piscataway, NJ: IEEE, 2014: 1-4.

[11] 胡莹,冀保峰,黄永明,等.大规模MIMO OFDMA下行系统能效资源分配算法[J].通信学报,2015,36(7):40-47.(HU Y, JI B F, HUANG Y M, et al. Energy-efficient resource allocation algorithm for massive MIMO OFDMA downlink system [J]. Journal on Communications, 2015, 36(7): 40-47.)

[12] 杨真真,杨震,孙林慧.信号压缩重构的正交匹配追踪类算法综述[J].信号处理,2013,29(4):486-496.(YANG Z Z, YANG Z, SUN L H. A survey on orthogonal matching pursuit type algorithms for signal compression and reconstruction [J]. Signal Processing, 2013, 29(4): 486-496.)

[13] DONOHO D L, TSAIG Y, DRORI I, et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit [J]. IEEE Transactions on Information Theory, 2012, 58(2): 1094-1121.

[14] 郎利影,王勇,白文庆,等.基于压缩感知CoSaMP算法的精确重构[J].计算机应用研究,2015,32(8):2554-2557.(LANG L Y, WANG Y, BAI W Q, et al. Accurate reconstruction of compressed sensing based on CoSaMP algorithm [J]. Application Research of Computers, 2015, 32(8): 2554-2557.)

[15] WANG X, NI L. Compressed sensing data reconstruction using a modified subspace pursuit algorithm under the condition of unknown sparsity [C]// Proceedings of the 2014 7th International Congress on Image and Signal Processing. Piscataway, NJ: IEEE, 2014: 1125-1129.

[16] WANG A, WANG Y, JIANG L. Improved sparse channel estimation for multi-user massive MIMO systems with compressive sensing [C]// Proceedings of the 2015 International Conference on Wireless Communications & Signal Processing. Piscataway, NJ: IEEE, 2015: 1-5.

Multi-cellchannelestimationbasedoncompressivesensinginMASSIVEMIMOsystem

LIU Ziyan*, TANG Hu, LIU Shimei

(CollegeofBigDataandInformationEngineering,GuizhouUniversity,GuiyangGuizhou550025,China)

Focused on the issue that the channel estimation accuracy of multi-cell multi-user MASSIVE Multi-Input Multi-Output (MASSIVE MIMO) system was poor in the case of low Signal-to-Noise Ratio (SNR), a compressive sensing algorithm named Fruit Fly Stagewise Orthogonal Matching Pursuit (FF-StOMP) based on group intelligent search was proposed. Based on the Stagewise Orthogonal Matching Pursuit (StOMP) solution to the channel matrix parameters and the normalized minimum mean square error under different thresholds, the algorithm was used to search the minimum normalized mean square error and its corresponding threshold by the fruit fly optimization algorithm to achieve the adaptive parameter setting. The simulation results show that the channel estimation performance of FF-StOMP algorithm can be improved by 0.5 to 1 dB when the SNR is 0 to 10 dB compared with the StOMP algorithm. When the SNR is 11 to 20 dB, the channel estimation performance can be improved by 0.2 to 0.3 dB. When the number of cell users changes, the proposed algorithm can realize the adaptive channel estimation, which can effectively improve the channel estimation accuracy in the case of MASSIVE MIMO system with low SNR.

MASSIVE Multi-Input Multi-Output (MASSIVE MIMO) technology; multi-cell channel estimation; adaptive compression sensing; Stagewise Orthogonal Matching Pursuit (StOMP) algorithm

2017- 03- 29;

2017- 05- 26。

贵州省科学技术基金资助项目(黔科合基础[2016]1054)；贵州省本科教学工程项目(SJJG201505)；贵州大学研究生创新基金资助项目(研理工2017015)。

刘紫燕(1974—)，女，贵州都匀人，副教授，硕士，主要研究方向：无线通信、嵌入式通信、大数据挖掘分析； 唐虎(1992—)，男，湖北荆州人，硕士研究生，主要研究方向：移动通信系统； 刘世美(1992—)，女，贵州毕节人，硕士研究生，主要研究方向：移动通信系统。

1001- 9081(2017)09- 2474- 05

10.11772/j.issn.1001- 9081.2017.09.2474

TN929.5

A

This work is partially supported by the Science and Technology Fund Project of Guizhou ([2016]1054); Guizhou Undergraduate Teaching Project (SJJG201505);Guizhou University Graduate Innovation Fund (Manager 2017015).

LIUZiyan, born in 1974, M. S., associate professor. Her research interests include wireless communication, embedded communication, big data mining analysis.

TANGHu, born in 1992,M. S. candidate. His research interests include mobile communication system.

LIUShimei, born in 1992,M. S. candidate. Her research interests include mobile communication system.