电磁干扰下合并单元常用算法的误差分析

兰春虎，范 巍，李盛伟，王兆峰，王 江

（1.国网天津市电力公司经济技术研究院，天津 300171；2.国网天津市电力公司电力科学研究院，天津 300384；3.国网天津市电力公司，天津 300010）

电磁干扰下合并单元常用算法的误差分析

兰春虎1，范 巍2，李盛伟1，王兆峰1，王 江3

（1.国网天津市电力公司经济技术研究院，天津 300171；2.国网天津市电力公司电力科学研究院，天津 300384；3.国网天津市电力公司，天津 300010）

本文旨在分析在取消电子式互感器出口二次转换器的前提下，合并单元能否克服电磁干扰的影响，输出符合规范要求的数据。在介绍电子式互感器的幅值及相位误差计算方法的基础上，列举了合并单元常用的几种数据处理算法。详细分析了三角自卷积窗算法的实现流程，并重点介绍了利用三角自卷积窗计算幅值、频率及初相角的方法。设计了一种基于LabVIEW的校验仪，模拟合并单元各类算法在不同信噪比条件下产生的误差，比较各算法的优劣。实验结果显示，合并单元可以通过软件算法消除电磁干扰的影响，提供误差范围符合规范要求的数据。

合并单元；电子式电流互感器；校验仪；三角自卷积窗；误差分析

自2009年5月，国家电网公司推出智能电网建设方案起至今，智能电网已从理论设想提升为工程建设标准，电子式互感器作为核心技术得到了大量的工程应用及深入的理论研究。在功能定位方面，相关国家标准及文献[1-2]规定，电子式互感器负责采集电流、电压信号，合并单元负责对来自电子互感器二次变换器的电流、电压信号做同步处理。目前主流观点认为二次变换器属于电子式互感器的一部分，以赵应兵等[3]为例，文中指出电子互感器必须在出口处经二次变换器实现信号数字化，并通过光纤对外传输。但由于二次变换器是分立器件，本身占据一定空间，在工程应用中暴露出没有空间安装的问题。针对该问题，本文考虑取消二次变换器，其功能由合并单元实现，使互感器输出的模拟信号通过电缆直接进入合并单元。为了通过实验手段分析各算法的抗干扰能力，设计了一种校验仪，验证在电磁干扰环境中，合并单元输出的数据能否满足相关规范要求。

1 采用傅里叶变换的误差计算

根据相关文献[1，4-9]中电子式互感器的误差定义，分析电子式电流互感器的幅值误差及相位误差计算过程如下。

一次电流幅值ip(tn)和被测互感器的二次电流数字量输出is(n)皆为周期性信号，这些信号数字化后的离散傅里叶变换分别为

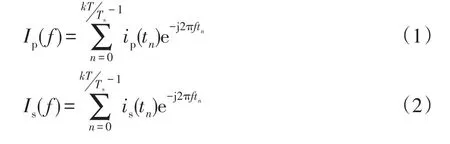
式中：T为一个工频周波的时间；n为数据集计数序号；tn为一次电流第n个数据集采样完毕时间；k为叠加周期数；Ts为一次电流两个样本之间的时间间隔。

对于额定频率的幅值误差和相位误差，分别为

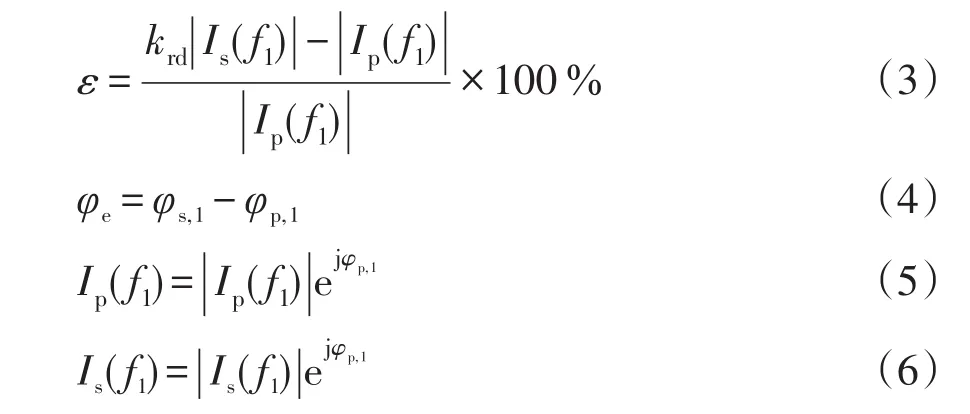
式中：ε为幅值误差；φe为相位误差，rad；Ip（f1）和Is（f1）分别为复数系数形式；krd为额定变比；φp为一次电流相位；φs为被试电流互感器的二次电流相位。

2 电子式电流互感器误差校验仪结构

为了对不同算法的抗电磁干扰能力进行量化分析，本文设计了一种校验仪[10-12]，包含硬件及软件两部分，结构图如图1所示，具体功能模块如下。

1）试验电流源

作为校验过程中的信号源，电流源具备足够的容量及调节精度，频率调整范围为[49.5 Hz，50.5 Hz]。

2）标准电流互感器

铁芯线圈的电流互感器准确度较高，且不受一次载流导体位置影响，适合作为标准电流互感器。本系统采用的标准电流互感器额定变比为1 000 A/1 A，准确度为0.05级。被测电子式电流互感器准确度为0.2S级。标准电流互感器的准确级比被测电子式电流互感器的准确级高2级，符合规范要求。

3）信号调理电路

通过电阻分压电路将标准电流互感器低压侧的电流信号转换成电压信号，便于计算机处理。

4）标准信号通道与被试信号通道

标准信号使用的数据传输通道有完善的屏蔽措施，可以忽略来自外界的干扰。被试信号使用的数据传输通道使用普通二次电缆，暴露在电磁干扰环境中，考虑工程实际中开关柜体尺寸，长度定为4 m。

5）数据采集卡

选用美国NI公司的PCI-4474完成标准电流互感器与被试电子式电流互感器的模数转换工作。其分辨率为24位，最小误差为6×10-8，满足校验仪在准确级方面的要求。在同步采样方面，PCI-4474使用外加时钟实现信号同步。由于基准信号和被试信号使用同一个数据采集卡完成信号处理，所以可以保证二者的采样同步性。

6）基于LabVIEW的误差分析平台

计算机使用Winpcap软件捕获PCI-4474发出的数据包，通过LabVIEW建立的分析平台，在后台计算出电子式互感器的比值差、相位差；在前台实现标准、被测信号的波形显示等功能。

图1 校验仪结构Fig.1 Structure of calibration equipment

3 合并单元主流数据处理算法分析

由于被试互感器的二次电缆暴露在强电磁干扰环境中，信号中含有大量噪声及谐波成分。因此要求合并单元算法能准确地提取出信号中的基频分量，这就需要分析不同信噪比背景下，合并单元常用的几种数据处理算法的优劣，得出能否克服干扰获得正确信号基频分量的结论。

合并单元常用的数据处理算法[13-16]有Blackman窗、Blackman-Harris窗、4项3阶Nuttall窗、4阶矩形卷积窗和4阶三角自卷积窗函数。前4类算法均可算作矩形窗的改进算法，其优势为对频率的辨识度高，但缺点是容易在频域变换时引入干扰及频谱泄漏；4阶三角自卷积窗函数与前述的矩形窗相比，实时性方面相差不大，但在减少频谱泄漏带来的误差方面存在明显优势，适合于有较强干扰的环境，以及对幅值、初相角等参数准确度要求较高的场合。考虑到减少干扰和提高精度的需求，本文重点介绍三角自卷积窗的实现流程，并就试验数据与其他窗函数对比、给出评价。

3.1 基于三角自卷积窗的基波参数分析方法

3.1.1 算法流程

基于三角自卷积窗的基波参数算法流程如图2所示，包括以下几个步骤：①对离散信号做截短处理，即进行长度为N的三角自卷积窗运算；②对加窗序列做傅里叶变换，获得其离散频谱；③在得到的频谱中搜索基波附近局部幅值最大谱线k1和次大谱线k2；④利用基于最小二乘法LSM（least square method）的多项式拟合算法求解频率偏移量λ；⑤计算基波频率、幅值和初相角等参数。

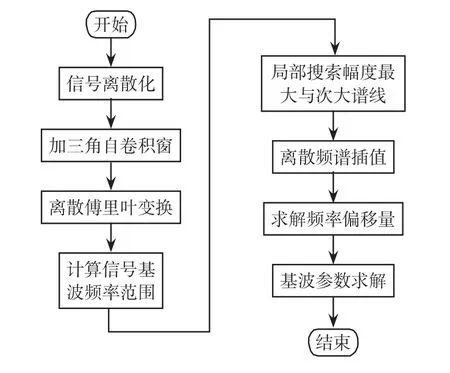
图2 算法流程Fig.2 Flow chart of algorithm

3.1.2 离散频谱插值算法

以频率单一的时域信号x（t）为例，经采样频率为fs的模数转换器后，得离散序列为

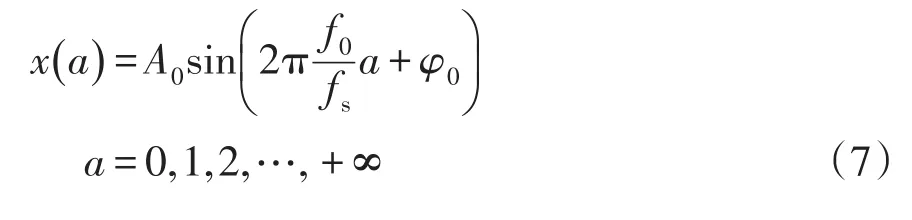
式中，A0、f0、φ0、a分别为信号的幅值、频率、初相角和各谐波较基波的频率倍数。

对离散后的信号加长度为N的p阶三角自卷积窗WTri-p(m)进行截短，其中，p阶三角自卷积窗计算式为

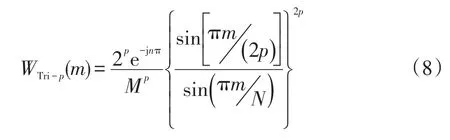
式中：m为各离散频谱序列号，m=0,1,…,N-1；M为三角自卷积窗的长度。

得到截短后的信号为

对截短后的信号做傅氏变换，得离散频谱为

式中，k0=f0N/fs代表基波频率f0在离散频谱中的位置。在工程应用中，模数转换的采样频率fs为常数值，而电力系统的基波频率f0往往存在波动。所以就算采用锁相环技术，采样频率fs也无法与基波频率f0保持严格的整数倍关系，即k0为非整数，位于离散频谱幅值最大谱线k1和次大谱线k2之间（k1≺k0≺k2=k1+1）。因此非同步采样在所难免，如图3所示。

图3 非同步采样情况Fig.3 Profile of non-synchronous sampling

在频率f0附近采用局部峰值搜索策略找到局部幅值最大和次大的谱线位置，分别为k1和k2，其中k0=k1+λ，λ代表频率偏移量，两条谱线幅值分别为y1和y2。为关于λ的复杂有理式，由于直接求解反函数计算量过大，故本文使用LSM法，用自定义参数α代替λ求解各参量。定义系数α和系数β分别为

由y1和y2可以计算出β，再利用频谱插值多项式计算出相应的α。

式中，a1,a2,…,ak为拟合多项式系数。

此时，频率f0、幅值A0和初相角φ0的计算式分别为

式中：x（k1）同式（10）中对x（k）的定义；arg表示求离散谱线的相角。

3.2 噪声影响下的基波参数提取试验

令信号源产生电子式电流互感器的额定电流信号，该信号同时含有基波、2次和3次谐波，使电子式电流互感器输出信号的时域表达式为

式 中 ：f0=50 Hz；A0=150 mV ；φ0=10°；A2=4 mV ；φ2=35°；A3=10 mV ；φ3=70°；fs=4 000 Hz。

据GB/T 20840.8—2007[1]中的规定，当前应用于电子式互感器的电磁兼容试验共包含2项辐射试验和11项抗扰度试验。考虑到单项试验的电磁环境与设备所在的真实电磁环境差距较大，本文将多项试验所用磁场混合，以达到模拟现场最恶劣条件下磁场环境的目的。通过分析上述13项试验报告，本文选取2项检出故障率最高的试验，即脉冲磁场抗扰度及阻尼振荡磁场抗扰度，以及最常用的工频磁场抗扰度试验，将三者产生的磁场混合形成本文的试验用磁场。将校验仪置于该混合磁场中，使被试信号通道中产生噪声。令信噪比以10 dB为步长，在[10 dB，100 dB]的范围内变化，对被试信号持续采样。分别采用长度为N=512的Blackman窗、Blackman-Harris窗、4项3阶Nuttall窗、4阶矩形卷积窗和4阶三角自卷积窗处理信号，并采用离散频谱插值校正算法求取信号的基波频率、幅值和初相角。各算法获取的基波参数随噪声强度变化的曲线分别如图4～图6所示。

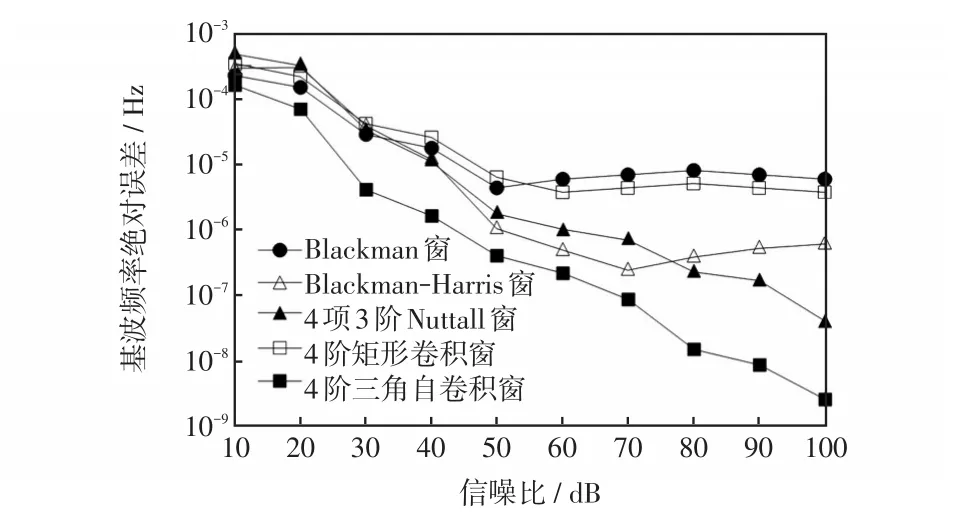
图4 基波频率绝对误差随信噪比变化的曲线Fig.4 Curves of the absolute error of fundamental waves’frequency vs signal-to-noise ratio

图5 基波幅值误差随信噪比变化的曲线Fig.5 Curve of the error of fundamental waves’amplitude vs signal-to-noise ratio

图6 基波初相角绝对误差随信噪比变化的曲线Fig.6 Curve of the absolute error of fundamental waves’initial phase angle vs signal-to-noise ratio

图4展示了合并单元的几大常用算法在不同信噪比的噪声环境中，提取基波频率的绝对误差分布曲线。4阶矩形卷积窗与Blackman窗所采集的基波频率误差相似，略高于其他3类算法的测量误差；4项3阶Nuttall窗和Blackman-Harris窗在信噪比大于50 dB后的测量结果准确度得到明显提高；使用4阶三角自卷积窗测得的基波频率准确度最高，且其优势在信噪比大于20dB后体现得淋漓尽致。

图5给出的是合并单元各常用算法在噪声环境中，提取基波幅值误差分布曲线。在信噪比小于50 dB时，各算法测得的基波幅值误差随信噪比的增大而迅速下降，但在[50 dB，60 dB]之间，Blackman-Harris窗、4项3阶Nuttall窗、4阶三角自卷积窗测量值误差会有小幅上升，在信噪比大于60 dB后，4阶矩形卷积窗与Blackman窗测量值的比差趋于常数，其他算法的误差则继续降低。在所有算法中，4阶三角自卷积窗的基波幅值误差最小。

图6给出了合并单元各常用算法在噪声环境中，提取基波初相角的绝对误差分布曲线。当信噪比不大于40 dB时，4阶矩形卷积窗与Blackman窗、Blackman-Harris窗、4项3阶Nuttall窗的误差相差不大，但均大于采用4阶三角自卷积窗测得基波初相角的绝对误差。当信噪比大于40 dB时，Blackman窗、Blackman-Harris窗、4项3阶Nuttall窗较4阶矩形卷积窗有明显优势，但准确度均低于采用4阶三角自卷积窗的情况。由图6可见，采用4阶三角自卷积窗的基波初相角准确度最高。

综上所述，4阶三角自卷积窗算法利用其优良的旁瓣性能，能够有效克服不同信噪比的噪声对基波参数分析的影响，其准确度高于采用Blackman窗、Blackman-Harris窗、4项3阶Nuttall窗、4阶矩形卷积窗的情况，特别当信噪比大于30 dB后，采用4阶三角自卷积窗进行基波参数提取的准确度明显高于其他4种窗函数。

上述试验数据还显示出，合并单元各主流算法在不同强度的噪声影响下，测得的基波频率绝对误差变化范围为[3.8×10-9Hz，5.9×10-4Hz]；基波幅值比差变化范围为[3.1×10-10，0.08×10-2]；基波初相角误差范围为[2.3×10-5′，3.1′]。满足 GB/T 20840.8—2007[1]规定的0.2S级计量用互感器误差限制要求。

4 结 语

本文介绍了电子式电流互感器误差校验仪的组成结构，建立了基于三角自卷积窗的FFT算法，还给出了基于三角自卷积窗的基波参数分析方法，并通过试验验证了合并单元各主流算法在基波参数分析中的有效性及准确性。实验结果显示，合并单元可以通过软件算法消除电磁干扰的影响，提供误差范围符合规范要求的数据。对于计量用电子式电流互感器，可以取消出口处的二次转换模块，使互感器输出的模拟信号通过电缆直接接入合并单元。

[1]GB/T 20840.8—2007，互感器第8部分：电子式电流互感器[S].2007.

[2]曹团结，尹项根，张哲，等（Cao Tuanjie，Yin Xianggen，Zhang Zhe，et al）.电子式互感器数据同步的研究（Discussion on data synchronization of electronic instrument transformers）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2007，19（2）：108-113．

[3]赵应兵，周水斌，马朝阳（Zhao Yingbing，Zhou Shuibin，Ma Zhaoyang）.基于IEC61850-9-2的电子式互感器合并单元的研制（Research and manufacture of merging unit based on IEC 61850-9-2）[J].电力系统保护与控制（Power System Protection and Control），2010，38（6）：104-106，110．

[4]毛安澜，叶国雄，吴士普，等（Mao Anlan，Ye Guoxiong，Wu Shipu，et al）.Rogowski结构电子式电流互感器复合误差的检测方法（The method of Rogowski structure of electronic current transformer composite errors calibration）[J].电测与仪表（Electrical Measurement&Instrumentation），2011，48（4）：30-35，44．

[5]周文中，赵国生，李海洋（Zhou Wenzhong，Zhao Guosheng，Li Haiyang）.Rogowski线圈测量误差分析及改进措施（Error analysis and improved method of Rogowski coil）[J].电力系统保护与控制（Power System Protection and Control），2009，37（20）：99-103，112．

[6]江亚群，杨勇，姜燕（Jiang Yaqun，Yang Yong，Jiang Yan）.电参量微机测量中随机误差的分析及抑制（Methods of restraning random errors in computer-based electric parameter measurement）[J].长沙电力学院学报：自然科学版（Journal of Changsha University of Electric Power：Natural Science），2002，17（4）：34-37．

[7]梁仕斌（Liang Shibin）.电流互感器复合误差的测量方法（Measuring methods of composite errors on current transformer）[J].继电器（Relay），2005，33（18）：79-83．

[8]尚秋峰，张静，董建彬（Shang Qiufeng，Zhang Jing，Dong Jianbin）.电子式电流互感器校准系统不确定度评定方法（Evaluation of measurement uncertainty for the calibration system of electronic current transformer）[J].电力系统自动化（Automation of Electric Power Systems），2008，32（18）：63-66 ．

[9]刘彬，叶国雄，郭克勤，等（Liu Bin，Ye Guoxiong，Guo Keqin，et al）.基于Rogowski线圈的电子式电流互感器复合误差计算方法（Calculation method of composite error for electronic current transformers based on Rogowski coil）[J].高电压技术（High Voltage Engineering），2011，37（10）：2391-2397 ．

[10]方婵畅（Fang Chanchang）.电子式互感器数字量输出校验系统（Calibration System for the Digital Output of Electronic Transformer）[D].武汉：华中科技大学电气与电子工程学院（Wuhan：College of Electrical&Electronic En-gineering，Huazhong University of Science and Technology），2011．

[11]王智东，陈俊威（Wang Zhidong，Chen Junwei）.采用IEDScout的新型继电保护实验平台（New relay experiment platform adopting IEDScout）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2015，27（6）：98-102．

[12]谭洪恩，胡浩亮，雷民，等（Tan Hong’en，Hu Haoliang，Lei Min，et al）.电子式互感器现场校准技术实验分析（Experimental analysis of on-site calibration of electronic instrument transformer）[J].高电压技术（High Voltage Engineering），2010，36（12）：2990-2995．

[13]童悦，张勤，叶国雄，等（Tong Yue，Zhang Qin，Ye Guoxiong，et al）.电子式互感器电磁兼容性能分析（Electromagnetic compatibility performance of electronic transformers）[J].高电压技术（High Voltage Engineering），2013，39（11）：2829-2835．

[14]胡浩亮，李前，卢树峰，等（Hu Haoliang，Li Qian，Lu Shufeng，et al）.电子式互感器误差的两种校验方法对比（Comparison of two electronic transformer error measuring methods）[J].高电压技术（High Voltage Engineering），2011，37（12）：3022-3027．

[15]李振华（Li Zhenhua）.电子式互感器性能评价体系关键技术研究（Research on the Key Techniques of Performance Evaluation System for Electronic Transformers）[D].武汉：华中科技大学电气与电子工程学院（Wuhan：College of Electrical&Electronic Engineering，Huazhong University of Science and Technology），2014．

[16]乔洪新，黄少锋，刘勇（Qiao Hongxin，Huang Shaofeng，Liu Yong）.基于二次插值理论的电子式互感器数据同步的研究（Discussion on data synchronization of electronic current transducer based on quadratic interpolation）[J].电力系统保护与控制（Power System Protection and Control），2009，37（15）：48-52．

Error Analysis of the Favorite Algorithms for Merging Units Under Electromagnetic Interference

LAN Chunhu1，FAN Wei2，LI Shengwei1，WANG Zhaofeng1，WANG Jiang3
（1.Economic Research Institute，State Grid Tianjin Electric Power Company，Tianjin 300171，China；2.Electric Power Research Institute，State Grid Tianjin Electric Power Company，Tianjin 300384，China；3.State Grid Tianjin Electric Power Company，Tianjin 300010，China）

On the promise of the cancellation of secondary converter of the electronic transformer’s output port，it is important to analyze whether the merging units can overcome the influence of electromagnetic interference and output the data that meet the requirements of specifications.Based on the introduction of the calculation methods for the electronic transformer’s amplitude error and phase error，some favorite data processing algorithms for the merging units are listed.The implementation process of triangular self-convolution window algorithm is analyzed，and the calculation method of the amplitude，frequency and initial phase angle with triangular self-convolution window is introduced.A kind of calibration equipment was designed based on LabVIEW.Various types of data processing algorithms for the merging units were tested at different signal-to-noise ratios to simulate the errors，and the test data were compared.The experimental results show that the software algorithms can remove the influence of electromagnetic interference on the merging units，thus the error in the data provided by the merging units was within a specified range.

merging unit；electronic current transformer；calibration equipment；triangular self-convolution window；error analysis

TM45

A

1003-8930（2017）10-0145-06

10.3969/j.issn.1003-8930.2017.10.024

2016-05-09；

2017-07-21

国家电网公司科技项目资助（项目号：KJ15-1-08）

兰春虎（1986—），男，硕士，助理工程师，研究方向为电力系统保护及自动化设计。Email：new096@163.com

范 巍（1984—），女，硕士，工程师，研究方向为电力系统科技咨询。Email：i_am_a_tiger@yeah.net

李盛伟（1982—），男，博士，高级工程师，研究方向为电力系统规划设计与施工。Email：18202534412@139.com