改进布谷鸟搜索算法在电力系统优化潮流中的应用
2017-11-14陈功贵邱思远郭艳艳黄山外刘利兰
陈功贵,邱思远,郭艳艳,黄山外,刘利兰
(1.重庆邮电大学自动化学院复杂系统分析与控制研究中心,重庆 400065;2.武汉铁路职业技术学院机车车辆工程系,武汉 430205)
改进布谷鸟搜索算法在电力系统优化潮流中的应用
陈功贵1,邱思远1,郭艳艳2,黄山外1,刘利兰1
(1.重庆邮电大学自动化学院复杂系统分析与控制研究中心,重庆 400065;2.武汉铁路职业技术学院机车车辆工程系,武汉 430205)
针对优化潮流的特点以及布谷鸟搜索算法收敛速度慢和缺乏活力等问题,从动态参数和步长方程两个方面进行改进,提出了改进的布谷鸟搜索算法来解决优化潮流问题。该算法把原来是常数的两个参数改进为动态变化的参数,随着迭代次数的增加,发现概率和步长因子两个参数按一定的规律递减,使算法在初期能增加种群的多样性,后期能更好地微调以找到最优解;同时,提出了一个具有最优解导向的搜索步长方程以提高算法的局部搜索能力和收敛速度。用改进的布谷鸟算法计算IEEE30系统的优化潮流,仿真结果表明该算法能够有效地提高收敛速度和计算精度。
布谷鸟算法;动态参数;电力系统;优化潮流
优化潮流OPF(optimal power flow)问题是通过电力系统中可调节的控制手段,在满足电力系统安全运行和物理约束条件的限制下,使某种预定目标达到最优的系统稳定运行状态[1]。OPF问题的主要目标是优化一个被选择的目标函数,例如系统的发电燃料费用函数、系统的有功损耗函数、无功补偿的经济效益函数等,而被广泛认为客观的函数是满足各种约束的发电燃料费用最优的函数[2]。
OPF是一个多变量、多约束、非线性的大型规划问题,广泛应用于电力系统的规划、运行和控制领域,具有重要的研究意义。为了解决OPF问题,人们提出了很多的优化算法,如线性规划法、非线性规划法、牛顿法、内点法以及智能算法等[3-5]。Yang等[6]提出了一种新颖的布谷鸟搜索CS(cuckoo search)算法,通过模拟布谷鸟的寄生育雏行为,利用Lévy飞行特征有效地求解最优问题。CS算法结构简单、参数少、鲁棒性强,具有较强的跳出局部最优的能力,其求解效率和计算精度均优于粒子群优化PSO(particle swarm optimization)算法和遗传算法GA(genetic algorithm)等智能算法。CS算法目前已经被应用到工程结构优化、流水车间调度等多种优化问题中,具有高效的性能和潜在的研究价值[7-8]。
为了改善CS算法的性能,提高该算法的效率和求解精度,本文提出了改进布谷鸟搜索ICS(improved cuckoo search)算法,对影响算法性能的两个重要参数——发现概率Pa和补偿因子α进行优化,把它们从不变的常系数变为动态变化的系数,使它们在算法的不同时期取得更合适的值[9];此外,对随机搜索步长进行了改进,在Lévy飞行中引入了“自我认知”和“社会认知”部分,以提高算法的局部搜索能力和收敛速度。将ICS算法应用到潮流计算中,仿真结果表明该方法有效地改善了CS算法的性能。
1 OPF问题的数学模型
1.1 目标函数
OPF问题是一个满足约束条件的目标最小化问题,即
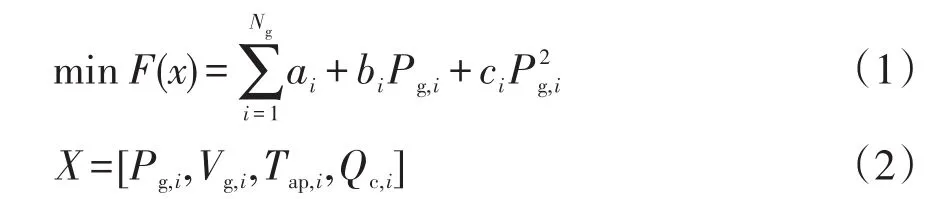
式中:F(x)为发电机的燃料费用;ai、bi和ci为第i台发电机的发电费用参数;Pg,i为第i台发电机的有功功率;Ng为发电机的台数;Vg,i为第i台发电机的电压值;Tap,i为第i个变压器的变比;Qc,i为第i个补偿电容器的无功功率。
然而,在实际应用中由于发电机的阀点效应,燃料费用曲线存在不可求导的点,优化问题变为非凸问题。当考虑发电机的阀点效应时,每个发电机的燃料费用函数要加一个相应正弦函数的绝对值,目标函数为
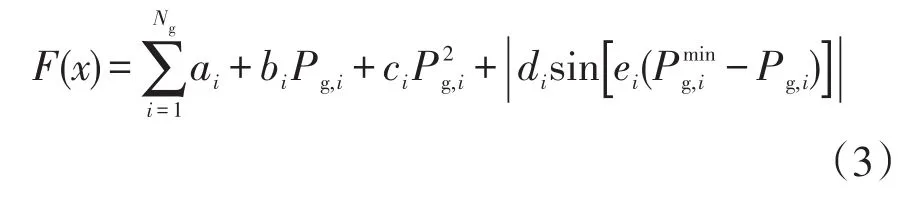
式中:di和ei分别为第i台发电机的阀点效应参数;为第i台发电机有功功率的最小值。
考虑和不考虑阀点效应的燃料费用曲线如图1所示,考虑阀点效应的燃料费用比不考虑阀点效应时要大,优化问题也变得更难解决。由于燃料费用曲线不是连续可导的,这给一些传统优化算法求解问题带来了困难,而智能算法则能更好地解决这些优化问题。
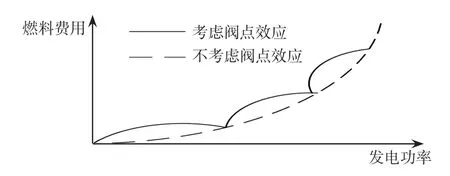
图1 考虑和不考虑阀点效应的燃料费用曲线Fig.1 Fuel cost curves with and without valve-point effect
1.2 等式约束
优化潮流问题的等式约束是电力系统的非线性潮流方程的集合,即

式中:Qg,i为发电机节点i的无功功率[10];Pd,i和Qd,i分别为相应负荷节点需要的有功功率和无功功率;N为节点数目;Vi和Vj分别为节点i和节点j的电压幅值;Gij和Bij分别为节点i和节点j的互电导和互电纳;θij为节点i和节点j之间电压的相角差。
1.3 不等式约束
优化潮流问题的不等式约束反映了电力系统设备的操作限制,能确保系统的安全运行,包括如下几个约束[11]。
(1)所有发电机节点的有功功率和无功功率必须满足

(3)并联电容器补偿的无功功率必须满足

式中,Nc为无功功率补偿数量。
(4)变压器的变比必须满足

式中,NT为变压器个数。
(5)支路视在功率必须满足
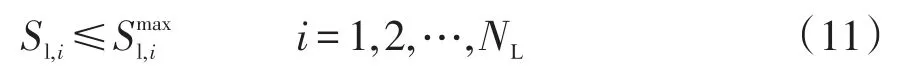
式中,NL为支路个数。
优化算法中有不同的方法来处理约束问题,本文把罚系数添加到适应度函数中去。分别用罚系数乘以对应变量越界数值的平方,并把它们加到目标函数上,得到最优化目标函数为
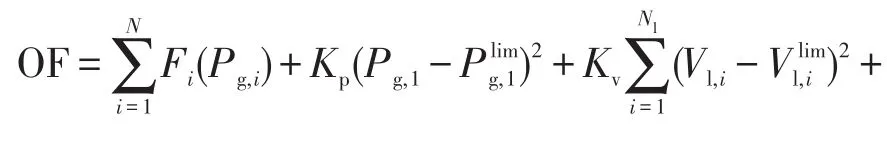

式中:Kp、Kv、Kq和Ks为罚函数的系数;Vl,i和Vliml,i为复合节点的电压值及其限制值;Xlim为变量X的限制值,其计算式为
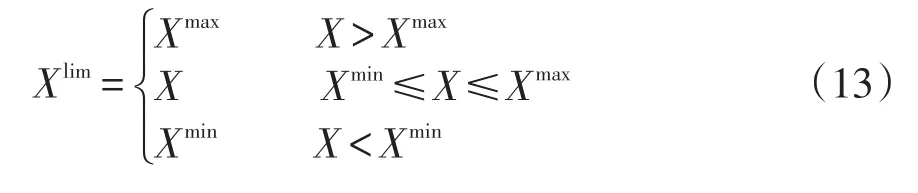
2 CS算法与ICS算法
2.1 CS算法
在自然界中,布谷鸟会将自己的蛋偷偷产在宿主的巢穴,并且朝着模拟宿主的蛋的颜色和样子的方向不断进化,以减小它们的蛋被发现的概率。通常情况下,布谷鸟的蛋会比宿主的后代孵化的早一点,而一旦被孵化出来,它的本能反应就会把其他的蛋都推出巢穴,并模拟宿主后代发出更响亮的叫声,以此得到更多的食物,增加自己存活的机率[9]。宿主有时候也会发现那些寄生的蛋,在这种情况下,宿主可能把寄生的蛋丢出巢穴,或者抛弃现在的巢穴并构建一个新巢。
CS算法是由布谷鸟的寄生育雏和Lévy飞行特征抽象出来的启发式算法,为此需要设定3个理想状态[12]:①每只布谷鸟一次只能产一个蛋,并随机放到一个宿主的巢穴里;②最好的鸟巢会被保留到下一代;③可利用的鸟巢数量是固定的,蛋被宿主发现的概率为Pa,Pa∈[0,1]。
在这3个设定的基础上,CS算法的基本步长公式可以被概括为
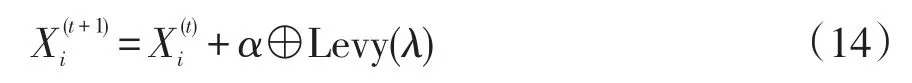
式中:Xi(t+1)为第t+1 代中的个体i;α为步长控制因子,与研究问题的规模有关,α>0;⊕表示点对点乘法;Levy(λ)为Lévy随机搜索路径,它的随机步长服从Lévy分布,即

这是布谷鸟不断跳跃的一个随机游走过程,它的步长满足一个重尾的稳定分布,在这种形式的行走中,短距离的行走与偶尔长距离的行走相间。此外,在每一代中都会有一部分鸟巢被发现,发现概率Pa∈[0,1]。在鸟巢更新过后,用随机数r∈[0,1]与Pa对比,当r>Pa时,相应的巢穴将被随机的新巢穴所替代,表达式为
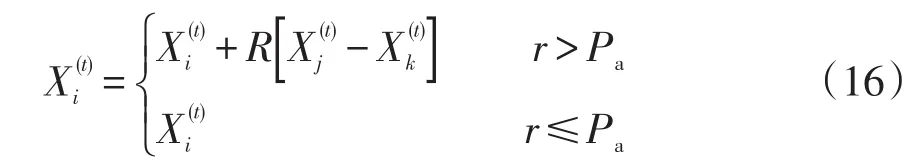
式中:R为一个在[0,1]区间上的随机数;Xj(t)和Xk(t)为第t代时两个随机的解。
2.2 ICS算法
2.2.1 动态参数的引入
在CS算法中参数Pa和α是非常重要的,它们可以用来加快算法的收敛速度并找到最优的解。但是在传统的CS算法中,参数Pa和α是固定不变的常数,这样就使得算法的收敛速度较慢。如果Pa的值太小而α的值太大,那么算法的性能将变差,收敛速度会慢很多;如果Pa的值太大而α的值太小,算法的收敛速度很快但可能得不到最优解[13]。
故而为了提高CS算法的性能并克服由于固定参数Pa和α带来的缺陷,在ICS算法中会使用动态变化的参数Pa和α。在算法迭代的早期,参数Pa和α的值应该足够大以增加解向量组的多样性。然而在迭代的后期参数Pa和α的值应该逐渐减小,这样解向量在最优解附近会有更好的微调,从而找到更优的解。参数Pa和α的值随着迭代次数而动态变化,其公式为

式中:Kmax为最大迭代次数;k为当前迭代次数;Pa_max为最大发现概率;Pa_min为最小发现概率;αmax为最大步长因子;αmin为最小步长因子。
2.2.2 步长改进
CS算法的基本原理是通过Lévy飞行产生步长,Lévy飞行的优点是有助于跳出局部最优解。然而Lévy飞行不能充分利用局部区域的信息,这主要是由于该机制的高度随机跳跃能力,使得局部搜索能力较差。
因此,为了提高CS算法局部搜索能力和收敛速度,借鉴了PSO算法的思想,在Lévy飞行中引入了“自我认知”和“社会认知”部分,将式(16)更改为
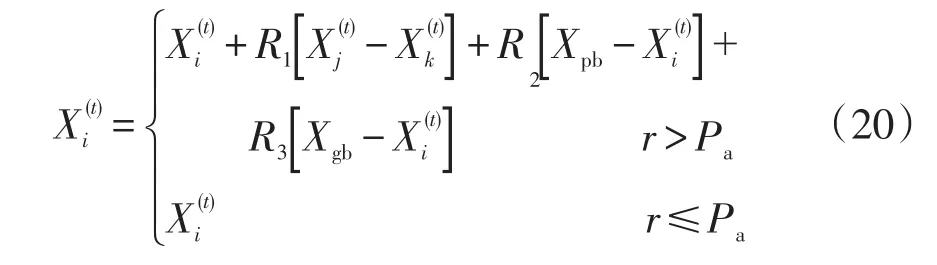
式中:R1、R2和R3均为在[0,1]区间上的随机数;Xpb和Xgb分别为个体最优解和全局最优解。与式(16)相比,式(20)增加了最优解引导算法寻优的搜索项,从而在随机搜索的基础上提高了算法的局部搜索能力。
在ICS算法中,Lévy飞行机制的高度随机性使得布谷鸟具有良好的前期搜索能力;而随着迭代次数的增加,发现概率Pa逐渐减小,使得按照式(20)更新的鸟巢数量增加,能够更好地在最优解附近搜索。这样ICS算法既有良好的全局搜索能力,又能提高局部搜索能力。ICS算法的具体步骤如下。
步骤1初始化种群,设置鸟巢的个数为n,搜索空间的维数为d,计算每个鸟巢的适应度。
步骤2对每个鸟巢按式(14)产生新的鸟巢,计算每个鸟巢的适应度,如果小于原来的适应度就用新的鸟巢替换旧的鸟巢。
步骤 3用一组n个随机数r(r∈[0,1])分别与发现概率Pa对比,保留发现概率小的鸟巢,并随机改变发现概率大的鸟巢。分别计算它们的适应度值,若新解优于旧解,则替换旧解。
步骤4找出最优的鸟巢和最优解,若不满足终止条件则返回步骤2继续进行迭代更新。
3 案例分析
本文在MATLAB R2013b环境下编制了ICS计算程序,对IEEE30测试系统进行了数值仿真分析,验证本文提出的最优潮流ICS算法的有效性。IEEE30节点测试系统如图2所示。

图2 IEEE30节点测试系统Fig.2 IEEE 30-node test system
IEEE30节点测试系统包含41条支路、4台变压器和9个无功补偿装置。9个无功补偿装置分别位于节点10、12、15、17、20、21、23、24和29处,4台变压器分别位于支路6-9、6-10、4-12和28-27上。此外有6台发电机,分别在节点1、2、5、8、11和13上,其中节点1为平衡节点。
ICS算法中的参数取值为Pa_max=0.5,Pa_min=0.1,αmax=0.5,αmin=0.05,λ=1.5。并取种群的个数为30,最大迭代次数Kmax=300,迭代精度ε=1×10-8。此外,在PSO算法中的加速因子a1、a2都取为2,惯性因子wmax=0.9,wmin=0.4。
IEEE30系统中发电机的有功功率约束范围和发电机费用参数如表1所示,控制变量的约束条件如表2所示。在种群个数和控制变量等设置相同的情况下,3种算法分别运行30次后,计算IEEE30系统燃料费用的最小值、平均值、最大值和标准偏差的统计结果如表3和表4所示,潮流计算的费用函数与迭代次数的平均收敛曲线如图3和图4所示。
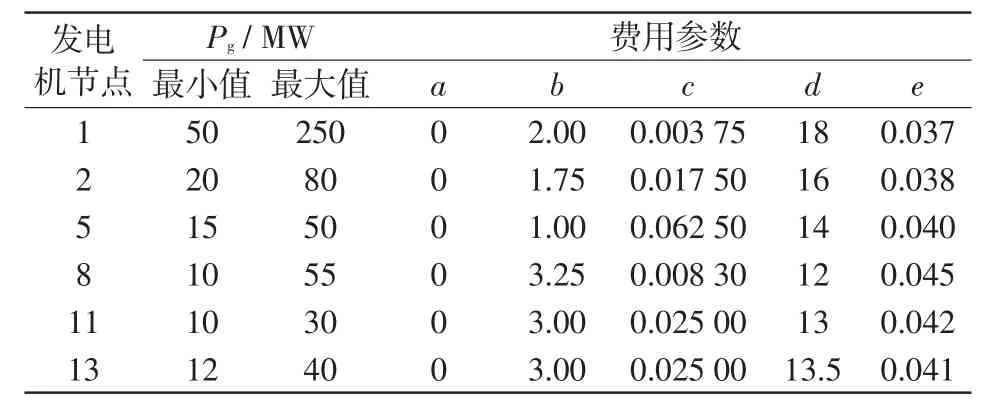
表1 IEEE30节点测试系统的发电机费用参数Tab.1 Electric generator cost parameters for IEEE 30-node test system

表2 控制变量的设置Tab.2 Configuration of control variables p.u.
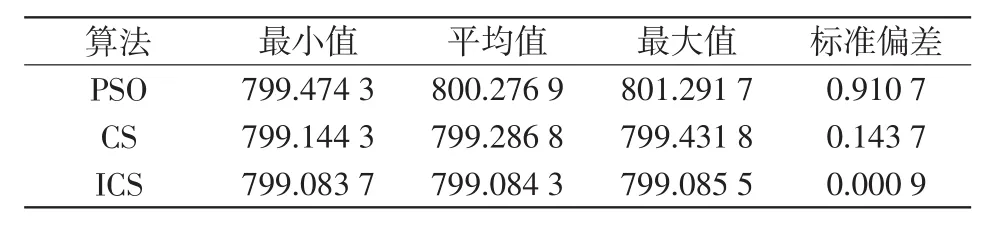
表3 不考虑阀点效应的燃料费用Tab.3 Fuel cost without valve-point effect $/h

表4 考虑阀点效应的燃料费用Tab.4 Fuel cost with valve-point effect $/h

图3 不考虑阀点效应的收敛曲线Fig.3 Convergence curves without valve-point effect

图4 考虑阀点效应的收敛曲线Fig.4 Convergence curves with valve-point effect
由表3可见,不考虑阀点效应时ICS算法得到的燃料费用为799.083 7$/h,比初始条件下的燃料费用降低了2.49%,优化效果最好,CS算法次之,PSO算法最差。从表4可以看出,考虑阀点效应时ICS算法的解也要优于PSO算法和CS算法。采用CS和ICS算法计算IEEE30系统的燃料费用值要小于PSO算法的计算值,说明前者具有良好的全局收敛性。由图3和图4可知,ICS算法的收敛速度和最优解均比CS和PSO算法的结果好,说明该算法确实提高了CS算法的收敛速度和计算精度。并且从表3和表4可以看出,ICS算法求得的燃料费用的标准偏差最小,表明该算法的鲁棒性很好,能够更稳定地得到最优解。
4 结 语
为了提高CS算法的收敛速度与计算精度,本文提出了ICS算法,从动态参数和具有最优解导向的步长方程两方面对算法进行改进。ICS算法前期有较大的步长和发现概率,使算法有更强的全局搜索能力,而迭代后期随着步长因子和发现概率的减小,该算法能够更好地微调以找到最优解。此外,具有最优解导向的步长方程能够提高收敛速度,增强局部搜索能力。采用MATLAB对CS算法和ICS算法进行编程实现,并应用到IEEE30测试系统的潮流计算中。仿真结果表明ICS算法不仅具有CS算法良好的全局收敛性和鲁棒性,并且比CS算法具有更佳的收敛速度和计算精度。
[1]聂永辉,肖白,刘凤兰(Nie Yonghui,Xiao Bai,Liu Fenglan).电力系统最优潮流新模型及其内点法实现(New optimal power flow model and its solution by using nonlinear interior point method)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2014,26(11):53-57.
[2]Ananthi Christy A,Vimal Raj P Ajay D.Adaptive biogeography based predator-prey optimization technique for optimal power flow[J].International Journal of Electrical Power and Energy Systems,2014,62:344-352.
[3]陈前宇,陈维荣,戴朝华,等(Chen Qianyu,Chen Weirong,Dai Chaohua,et al).基于改进 PSO 算法的电力系统无功优化(Reactive power optimization based on modified particle swarm optimization algorithm for power system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2014,26(2):8-13,43.
[4]丁涛,柏瑞,郭庆来,等(Ding Tao,Bo Rui,Guo Qinglai,et al).一种非迭代仿射算法的输电网区间潮流计算方法(A non-iterative affine arithmetic methodology for interval power flow analysis of transmission network)[J].中国电机工程学报(Proceedings of the CSEE),2013,33(19):76-83.
[5]陈丽光,文波,聂一雄(Chen Liguang,Wen Bo,Nie Yixiong).基于退火粒子群和内点法的改进最优潮流算法(Improved optimal power flow algorithm based on annealing particle swarm and interior point method)[J].广东电力(Guangdong Electric Power),2013,26(9):32-35,103.
[6]Yang Xin-She,Deb S.Engineering optimisation by cuckoo search[J].International Journal of Mathematical Modelling and Numerical Optimisation,2010,1(4):330-343.
[7]陈乐,龙文(Chen Le,Long Wen).求解工程结构优化问题的改进布谷鸟搜索算法(Modified cuckoo search algorithm for solving engineering structural optimization problem)[J].计算机应用研究(Application Research of Computers),2014,31(3):679-683.
[8]Marichelvam M K.An improved hybrid cuckoo search(IHCS)metaheuristics algorithm for permutation flow shop scheduling problems[J].International Journal of Bio-Inspired Computation,2012,4(4):200-205.
[9]Valian E,Mohanna S,Tavakoli S.Improved cuckoo search algorithm for global optimization[J].International Journal of Communications and Information Technology,2011,1(1):31-44.
[10]陈碧云,韦杏秋,陈绍南,等(Chen Biyun,Wei Xingqiu,Chen Shaonan,et al).基于多种群遗传算法的电力系统多目标优化(Power system multi-objective optimization based on multi-population genetic algorithm)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2015,27(7):24-29.
[11]Chen Gonggui,Liu Lilan,Song Peizhu,et al.Chaotic improved PSO-based multi-objective optimization for minimization of power losses and L index in power systems[J].Energy Conversion and Management,2014,86:548-560.
[12]Thang Trung Nguyen,Dieu Ngoc Vo,An Viet Truong.Cuckoo search algorithm for short-term hydrothermal scheduling[J].Applied Energy,2014,132:276-287.
[13]Valian E,Tavakoli S,Mohanna S,et al.Improved cuckoo search for reliability optimization problems[J].Computers&Industrial Engineering,2013,64(1):459-468.
Application of Improved Cuckoo Search Algorithm to Optimal Power Flow in Power System
CHEN Gonggui1,QIU Siyuan1,GUO Yanyan2,HUANG Shanwai1,LIU Lilan1
(1.Research Center on Complex Power System Analysis and Control,College of Automation,Chongqing University of Posts and Telecommunications,Chongqing 400065,China;2.Department of Locomotive and Vehicle Engineering,Wuhan Railway Vocational College of Technology,Wuhan 430205,China)
Considering the characteristics of optimal power flow(OPF),as well as the problems of cuckoo search(CS)algorithm such as slower convergence rate and the lack of flexibility,an improved cuckoo search(ICS)algorithm is proposed by modifying the dynamic parameters and the equation of step length.The proposed ICS turns two formerly constant parameters into dynamically changing parameters,and it is found that the probability and step length factor decrease with the increase of iteration numbers,so that the diversity of seed groups is improved in the early generations and the optimal solution can be found with a better fine-tuning in the final generations.In addition,a step length equation oriented for optimal solution is proposed to further improve the local search ability and the convergence rate of the algorithm.The ICS algorithm is used to compute the OPF of an IEEE 30-node system,and the results show that it can improve the convergence rate and calculation accuracy effectively.
cuckoo search(CS)algorithm;dynamic parameter;power system;optimal power flow(OPF)
TM744
A
1003-8930(2017)10-0030-05
10.3969/j.issn.1003-8930.2017.10.006
2015-11-06;
2017-03-11
国家自然科学基金资助项目(51207064,51507024);重庆市科委科技资助项目(KJI500401)
陈功贵(1964—),男,博士,教授,研究方向为电力系统优化调度。Email:chenggpower@126.com
邱思远(1992—),男,硕士研究生,研究方向为电力系统优化调度。Email:qiusypower@163.com
郭艳艳(1970—),女,硕士,副教授,研究方向为电力系统分析。Email:425092059@qq.com
