三电平逆变器SHEPWM技术的所有解问题

叶满园，李 宋，蔡 鸿

（华东交通大学电气与自动化工程学院，南昌 330013）

三电平逆变器SHEPWM技术的所有解问题

叶满园，李 宋，蔡 鸿

（华东交通大学电气与自动化工程学院，南昌 330013）

针对多电平逆变器特定谐波消除SHEPWM（selective harmonic elimination pulse-width modulation）求解非线性方程组对开关角度初值依赖性高的问题，采用三角函数倍角关系将三电平中点钳位NPC（neutral point clamped）逆变器SHEPWM非线性方程组转换为代数多项式的模式，并利用MATLAB中的Solve函数对多项式模型进行求解，在无需开关角初值的情况下得到了全调制比下的所有解。给出了开关角及线电压谐波失真THD（total harmonics distortion）随调制比变化的轨迹，分析和比较了开关角解的分布特点，为实际工程中开关角度的选取提供了理论依据。最后仿真和实验验证了利用Solve函数所求开关角度的正确性和可行性。

三电平逆变器；代数多项式；消谐模型；开关角初值

20世纪80年代日本学者Nabael提出了三电平中点钳位NPC（neutral point clamped）逆变器，该拓扑具有容量大、输出电压谐波小、能量可双向流动等优点，而被广泛应用于高压变频及机车牵引等领域。

适用于NPC逆变器的调制方法主要有多载波正弦脉宽调制技术、电压空间矢量调制技术和特定谐波消除调制技术SHEPWM（selective harmonic elimination pulse-width modulation）[1-4]。其中 SHEPWM技术具有开关频率低、器件损耗小、输出波形质量好、逆变效率高等优点，受到了广泛的关注。文献[5]对SHEPWM初值问题进行了研究，提出了质心重合的初值选定方法，减小了初值选取的难度，但是在该方法中一组初值只能得到一组解；文献[6]提出的同伦算法具有很宽的收敛域，对初值的要求不高；文献[7]采用Walsh函数将傅里叶域下的非线性超越方程组变换为Walsh函数域下的分段线性方程组进行求解，该方法使得SHEPWM在线计算开关角度的实时控制成为可能；文献[8-9]利用三角函数倍角关系将SHEPWM非线性方程组转换成代数多项式方程组，并运用合成理论对方程组进行求解的方法，得出了非线性方程组的所有解，且该种方法不需要初值，但采用合成理论求解多项式其计算量大、计算速度慢，在开关切换角个数较多时甚至无法完成计算。

本文将SHEPWM非线性方程组转换成代数多项式方程组形式，并直接利用数学软件MATLAB中的Solve函数对代数多项式进行求解，相比于传统代数多项式求解法，如Groebner基法和吴方法，该方法实现简单、运算速度快，并且可以获得比较好的消谐效果。

1 NPC逆变器拓扑及原理

三电平NPC逆变器拓扑结构如图1所示，以A相桥为例，A相输出电压有以下3种情况：当开关器件S1、S2导通，S3、S4关断时，A相输出电压为+Ud/2（Ud为母线电压）；当开关器件S3、S4导通，S1、S2关断时，A相输出电压为-Ud/2；当开关器件S2、S3导通，S1、S4关断时，A相输出端电位等于Z点电位，电压为0。

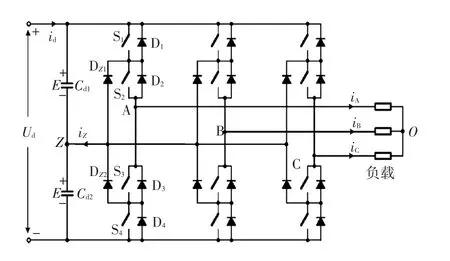
图1 三电平NPC逆变器拓扑结构Fig.1 Topological structure of three-level NPC inverter

2 NPC逆变器SHEPWM模型的建立

三电平NPC逆变器SHEPWM模型单相输出相电压波形如图2所示，由于波形呈1/4周期对称性，因此满足Dirichlet定理，A相相电压的傅里叶展开式为

其中：

由于相电压波形1/4周期轴对称，只包含奇次谐波，因此可得

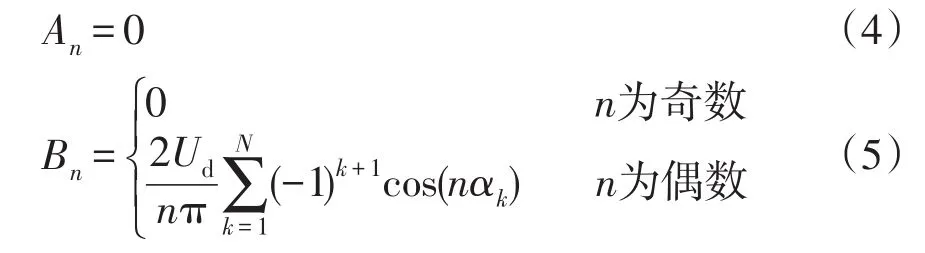
式中：N为1/4周期内开关角个数；αk为各开关角度，且开关角度约束条件为

本文针对三电平NPC逆变器，欲消除5、7次谐波，依据式（5）可得消谐模型为

式中，m为调制比，，B1为基波系数。

图2 三电平NPC逆变器SHEPWM模型单相输出相电压波形Fig.2 Waveform of single phase voltage of three-level NPC inverter SHEPWM model

3 模型的求解

3.1 模型变换

由三角函数运算可知，5倍角和7倍角的展开形式为

令cosθ1=x1，cosθ2=x2，cosθ3=x3，结合式（7）～式（9），可以将三角函数表示的SHEPWM模型转换为代数多项式表示的SHEPWM模型，即

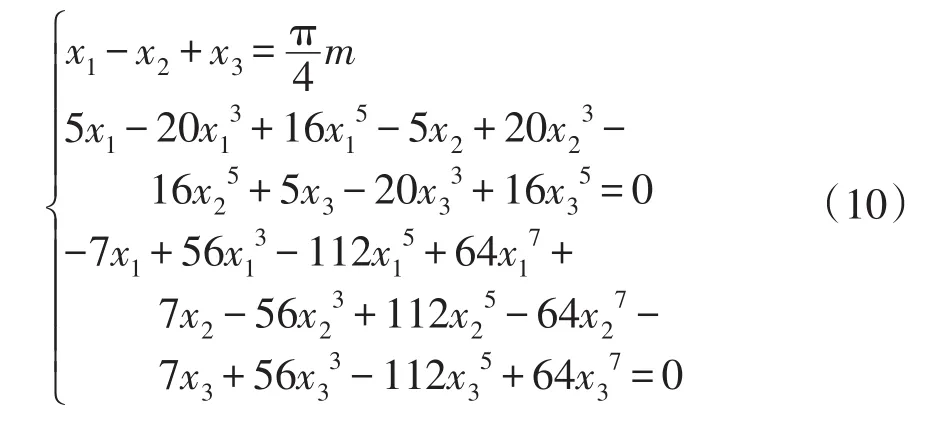
式中，1＞x1＞x2＞x3＞0

3.2 模型求解及结果分析

本文采用可以求解得到方程组的所有解，且不需要初值的符号解法。通过研究发现，数学软件MATLAB中提供了专门解决代数方程（组）的符号（解析）解的函数——Solve函数，利用它可以求解本文的代数多项式模型，该方法简单且不需要初值。本文利用该方法对三电平NPC逆变器的SHEPWM模型进行了求解。

以调制比m=0.9为例说明计算过程：

（1）将调制比m=0.9代入式（10）；

（2）对方程组（10）进行求解得到两组解，分别为[x1x2x3]=[0.978 6 0.369 4 0.090 8]和[0.868 4 0.772 5 0.604 2]；

（3）将得到的x1、x2、x3进行反余弦运算，[θ1θ2θ3]=[arccosx1arccosx2arccosx3]得到了调制比m=0.9时的两组开关角解，第1组解为[11.867 0°68.322 5°84.793 0°]，第2组解为[29.730 7°39.418 8°52.831 6°]。

按上文中所述步骤求解出三电平逆变器全调制比下的所有解，并绘制了其随调制比变化的轨迹，如图3所示。

图3 三电平逆变器解的轨迹Fig.3 Solution trajectory of three-level inverter

4 仿真验证

为了验证计算结果的正确性，利用软件MATLAB/Simulink搭建了NPC仿真实验模型，并对算例中调制比为0.9时的两组解进行了仿真研究。图4和图5分别为两组开关角下，相电压UAN、线电压UAB波形及其频谱。

图4 第1组解的电压波形及频谱

图5 第2组解的电压波形及频谱Fig.5 Voltage waveforms and spectra of the second set of solutions

从图4和图5中的仿真波形可见，输出电压中的5次和7次谐波基本上都已被消除，由此可以验证理论分析中求解SHEPWM开关角的正确性。同时也证明了轨迹中高调制比下的两组解都能满足SHEPWM的要求，都是有效解。

为了进一步研究所求开关角的SHEPWM效果，将图3中获得的开关角，逐一进行仿真并记录其THD大小，从而获得了NPC逆变器全调制比下THD含量分布曲线图（调制比0～0.12部分未画出），如图6所示。其中，虚、实两曲线分别对应为图3中同线型开关轨迹的THD。

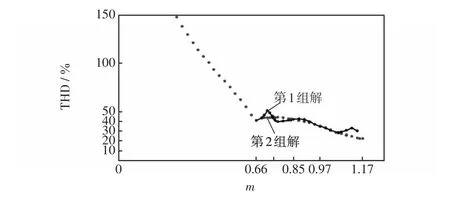
图6 NPC逆变器的THD曲线Fig.6 THD curves of NPC inverter

5 实验研究

为了验证两组解在工程中的实际SHEPWM效果，本文搭建了NPC逆变器实验平台。直流侧电容采用22 V直流电压源代替，输出电压频率50 Hz，负载采用168 Ω水泥电阻，分别对调制比m=0.9时的两组解进行了实验。其相电压、线电压波形及频谱如图7和图8所示。

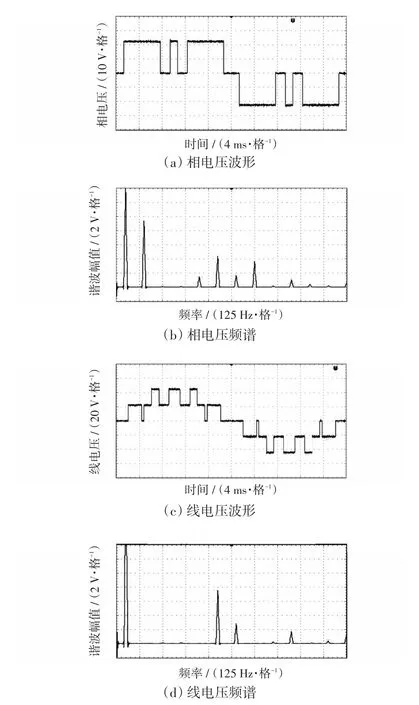
图7 第1组解实验波形Fig.7 Experimental waveforms of the first set of solutions

图8 第2组解实验波形Fig.8 Experimental waveforms of the second set of solutions

从相、线电压的频谱可以看出，两组解的5、7次以及3倍频的谐波均已消除，从而验证了两组解的正确性。

6 结 语

本文将NPC逆变器SHEPWM数学消谐模型转换为代数多项式的形式，并利用MATLAB中的Solve函数对其进行求解，得到了全调制比下的所有解，并绘制了开关角及其对应的线电压谐波含量随调制比变化的曲线，为实际工程控制时对SHEPWM开关角的选取提供了一定的理论依据。仿真和实验结果证明了利用三角函数倍角关系将SHEPWM非线性方程组转换成代数多项式，并结合Solve函数求解开关角的方法是可行的，可以求得SHEPWM方程组的所有解，而且该方法同样适用于其他SHEPWM控制的场合。

[1]Sirisukprasert S，Lai J S.A novel cascaded multilevel converter drive system with minimum number of separated DC sources[J].IEEE PEDS，2011，12（9）：45-49.

[2]何大清，危韧勇（He Daqing，Wei Renyong）.H桥级联型静止无功发生器研究（Research on H-bridge cascaded static var generator）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2006，18（4）：97-100.

[3]刘桂英，邓明锋，粟时平，等（Liu Guiying，Deng Mingfeng，Su Shiping，et al）.H桥级联STATCOM直流侧电压控制新方法（DC voltage control method of H bridge cas-caded STATCOM）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2015，27（10）：48-55.

[4]Xu Ning，Xu Heyi，Hu Haihong.Three-phase cascaded multi-level shunt active power filter[J].Proceedings of the CSU-EPSA，2014，26（3）：57-60.

[5]费万民，阮新波，张艳莉，等（Fei Wanmin，Ruan Xinbo，Zhang Yanli，et al）.多电平逆变器特定谐波消除脉宽调制方法的初值问题研究（Research on the initial values of SHEPWM method for multi-level voltage inverters）[J].中国电机工程学报（Proceedings of the CESS），2007，27（13）：87-92．

[6]谢运祥，周炼，彭宏（Xie Yunxiang，Zhou Lian，Peng Hong）.逆变器消谐PWM模型的同伦算法研究（Homotopy algorithm research of the inverter harmonic elimination PWM model）[J].中国电机工程学报（Proceedings of the CESS），2000，20（10）：23-26．

[7]郑春芳，张波，丘东元（Zheng Chunfang，Zhang Bo，Qiu Dongyuan）.基于Walsh变换的多电平逆变器谐波消除技术（Selective harmonic elimination technique based on Walsh transform for multilever inverters）[J].电工技术学报（Trans of China Electronics Society），2006，21（9）：81-87．

[8]Chiasson J N，Tolbert L M，McKenzie K，et al.A complete solution to the harmonic elimination problem[J].IEEE Trans on Power Electronics，2003，19（2）：596-603．

[9]Chiasson J N，Tolbert L M，McKenzie K J，et al.A unified approach to solving the harmonic elimination equations in multilevel converters[J].IEEE Trans on Power Electronics，2004，19（2）：478-490．

Complete Solutions for SHEPWM of Three-level Inverter

YE Manyuan，LI Song，CAI Hong
（School of Electrical and Automation Engineering，East China Jiaotong University，Nanchang 330013，China）

Aiming at the problem that the selective harmonic elimination pulse-width modulation（SHEPWM）of a multi-level inverter has a high dependence on the initial values of switching angle in the solving process of nonlinear equations，double-angle trigonometric functions are used in this paper to convert the nonlinear equations of SHEPWM of three-level neutral point clamped（NPC）inverter into an algebraic polynomial mode，and all the solutions in full modulation region can be obtained by using the“Solve”function in MATLAB to process the polynomial model without the need to know the initial values of switching angle.The trajectories of switching angles and the corresponding total harmonic distortion（THD）of line voltage，which vary with the modulation ratio，are also given.Moreover，the distribution characteristics of the solutions of switching angles are analyzed and compared，which provides a theoretical reference for the selection of switching angles in practical engineering.Finally，the correctness and feasibility of using the“Solve”function to compute the switching angles is verified by simulations and experiments.

three-level inverter；algebraic polynomial；harmonic elimination model；initial value of switching angle

TM464

A

1003-8930（2017）10-0018-04

10.3969/j.issn.1003-8930.2017.10.004

2015-10-08；

2017-04-06

国家自然科学基金资助项目（51167006）；江西省工业科技支撑计划资助项目（20161BBE50057）；江西省自然科学基金资助项目（20161BAB206157）；江西省教育厅自然科学基金资助项目（GJJ160495）

叶满园（1978—），男，副教授，研究方向为电力电子与电力传动。Email：yemanyuan1@163.com

李 宋（1977—），女，硕士，副教授，研究方向为电力电子与电力传动。Email：jxlisong1@163.com

蔡 鸿（1988—），男，硕士研究生，研究方向是电力电子与动力传动。Email：645653463@qq.com