基于多变量时间序列反演自记忆模型的中长期电力负荷预测
2017-11-14邹品晶姚建刚孔维辉胡淋波潘雪晴
邹品晶,姚建刚,孔维辉,胡淋波,潘雪晴
(湖南大学电气与信息工程学院,长沙 410082)
基于多变量时间序列反演自记忆模型的中长期电力负荷预测
邹品晶,姚建刚,孔维辉,胡淋波,潘雪晴
(湖南大学电气与信息工程学院,长沙 410082)
电力负荷预测的复杂性、非线性使传统的中长期预测模型难以获得精确的结果。为了提高中长期电力负荷预测准确度,构建了多变量时间序列反演自记忆模型。该模型使用灰色关联分析选取电力负荷变化主要影响因素,采用主要影响因素对电力负荷自身变化过程进行动力方程反演,并结合自记忆模型,实现对电力负荷数据的拟合与预测。在提高预测精度的同时,使预测结果最大程度地体现历史电力负荷数据的内在变化规律,提高拟合和预测的稳定性。为了验证模型的效果,使用1986—2002年某地区全社会用电量数据作为训练样本,进行拟合分析,并预测2003—2006年全社会用电量。拟合和预测的结果证明了该模型在中长期负荷预测中的有效性和可行性。
中长期电力负荷预测;灰色关联分析;主要影响因素;动力方程反演;自记忆模型
中长期电力负荷预测是电力系统调度运行、发展规划的前提,其精度对电力系统的安全、稳定、可靠、经济运行起着至关重要的作用[1-2]。中长期负荷预测方法很多,目前中长期电力负荷预测的方法大致可分为经典预测方法和基于新兴学科理论的现代预测方法两类。其中,经典方法主要包括电力弹性系数法、时间序列法、回归分析法等[3-7];现代预测技术主要包括灰色理论法、神经网络预测技术、支持向量机方法等[8]。两类方法各有其优缺点,经典预测方法预测效果较差,但操作简单,易于理解。现代预测技术中,灰色系统理论用指数方程拟合累加生成时间序列,当累加时间序列具有灰色指数规律时预测精度较高,但电力负荷累加时间序列一般并不具备指数规律,或有指数规律,但仅仅是近似指数规律[9-10],这使得灰色预测模型往往误差较大。神经网络预测方法能够对大量非结构性、非精确性规律具有自适应能力,但是神经网络的层数和神经元个数多依据主观经验确定,难以科学地确定其网络结构。支持向量机具有较好的泛化能力、强大的非线性处理能力和高位处理能力[11],但是支持向量机并不能深度挖掘数据自身变化规律。
电力负荷具有确定性,也具有其随机性[12]。一方面电力负荷的变化受到经济、人口、气候等众多因素的综合制约,有其自身的内在发展规律性,表现为其历史数据一般存在承续关系,为一动态变化过程。另一方面电力负荷的变化往往是因为某种因素的较大变化,表现为某段历史数据具有一定随机性。因此,在对电力负荷历史数据进行分析时宜采用随机-动力相结合的方式。动力系统自记忆原理[13]就是一种随机-动力方法,它将动力学计算与利用历史数据估算记忆系数相结合,同时吸取统计学中从过去观测资料中提取预测信息的优点。它比以往单一的确定论或随机统计论预测方法具有更高的拟合精度和预测准确率。
本文以电力负荷历史数据及电力负荷相关影响因素历史数据看作描述实际非线性系统动力模式的一系列特解,通过反演计算可获得模拟系统演化过程的非线性动力微分方程。求得系统动力微分方程之后,结合自记忆原理,建立多变量时间序列反演自记忆模型,并将其应用于实际中长期电力负荷预测。这种方法既考虑了电力负荷各影响因素对其的影响,也计及电力负荷时间序列自身变化趋势,方便实用且具有较好的预测精度。
1 时间序列记忆性
1.1 时间序列记忆长度确定
时间序列的记忆性体现着序列未来状态的发展与序列现在和过去的状态相关。对于一个具体的时间序列,存在一个记忆长度,当一个状态经过的时间超过记忆长度时,该状态的记忆性将消失,即不再对未来起作用。
时间序列的记忆长度,一般可采用R S分析来确定[14-15]。对于时间序列{x(t)}(t=1,2,…,n),对于任意正整数τ≥1,可求取均值序列累积离差为极差序列为标准差序列为定义统计量为

1.2 自记忆原理

定义相应的范数为

式(3)满足Cauchy-Schwarz不等式

将内积空间完备化就得到Hilbert空间H。可将多时次模式的解视为H中的广义解。设系统演化的微分方程为

式中:J为整数;xi为第i个变量;λ为参数。为简化计算,本文仅研究电力负荷自身的演化,所以下文中只用一个变量x来表述。设所讨论的变量和函数皆连续、可微、可积,定义记忆函数为

由于本文的推导固定在空间点ri上,故下文在β中将省略r的描述,将式(2)中定义的内积代入式(5)和式(6),积分区间取t0~t,可得
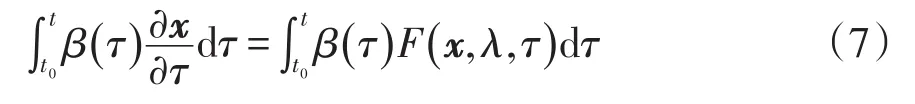
显然,可将式(7)看作式(5)的加权积分,权重即为记忆函数。
对式(7)左边运用分部积分,得


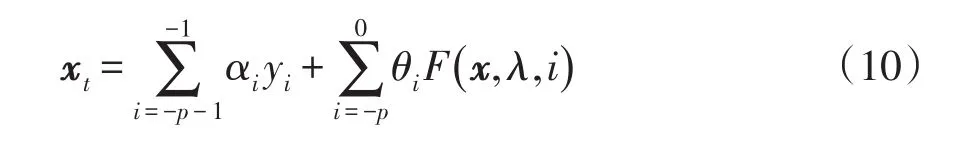
2 多变量时间序列反演自记忆模型建模
2.1 电力负荷影响因素灰关联分析
电网规划中长期负荷预测影响因素较多,如第一、二、三产业产值、国民生产总值和人口等[16-18]。为了更好地反映电力负荷的变化规律,需要将其各影响因素在建模时考虑进去。因为影响因素众多,所以有必要对各因素进行主次区分,一般可采用相关分析、显著性检验和回归分析等传统方法来确定各因素的主次关系。但是这些方法往往需要较大的样本数据,同时要求样本有较好的规律性,而且有时可能会出现量化结果和定性分析相互矛盾的情况,使其不能客观地评价各影响因素的主次关系。
灰关联分析方法[19]是灰色系统理论的重要内容,该方法旨在找出系统行为特征序列和影响因素序列的关联度,从关联度的大小来区分各影响因素的主次关系,其主要计算过程如下:假设某一电力负荷时间序列为:个影响因素组成的时间序列为则和在t时刻的灰色关联系数为

其中

灰色关联度计算公式为

通过比较灰色关联度εi的大小,就可以找出电力负荷的主要影响因素。
2.2 多变量时间序列反演理论
在实际中,电力负荷时间序列一般可以得到,但是能够模拟其自身演化的微分动力方程却往往难以得到。电力负荷的变化具有非线性和复杂性,其发展同时受到多种因素的影响,而且其自身变化并非按照严格数学规律进行,因此,要想得到能够模拟其演化过程的动力微分方程,需要以实际历史数据为基础进行反演。
假设电力负荷为x,其影响因素用zi(i=1,2,…,m)表示,则建立其动力微分方程为


式中:K为非线性多项式的项数;Qk为第k个多项式,Qk一般为各因素自身的多次项或者各因素多次项的乘积,在实际应用中,多次项的幂一般不超过3;qk为第k个多项式的系数,qk同样可采取最小二乘法求解。考虑长度为n的时间序列,均采用上述方式构建微分方程,用矩阵形式对其进行描述,即

2.3 基于多变量时间序列反演自记忆模型的中长期电力负荷预测
根据第2.2节所述方法可得到电力负荷微分动力方程,结合自记忆原理,可构建多变量时间序列反演自记忆模型为
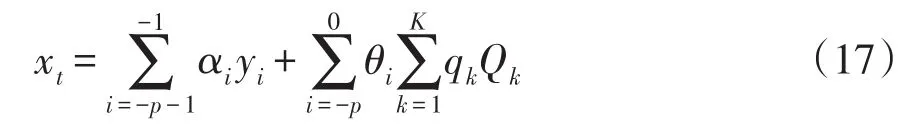
可将式(17)转化为矩阵形式得


基于多变量时间序列反演自记忆模型的中长期电力负荷预测算法流程如图1所示,具体步骤如下:
步骤1分别构建长度为n的电力负荷和各影响因素历史序列;
步骤2计算电力负荷与各影响因素的灰色关联度εi,通过比较εi的大小,筛选出电力负荷主要影响因素;
步骤3结合多变量时间序列反演理论,反演电力负荷自身演化动力微分方程,并通过最小二乘法求取各多项式系数qk;
步骤4设定回溯阶为p;
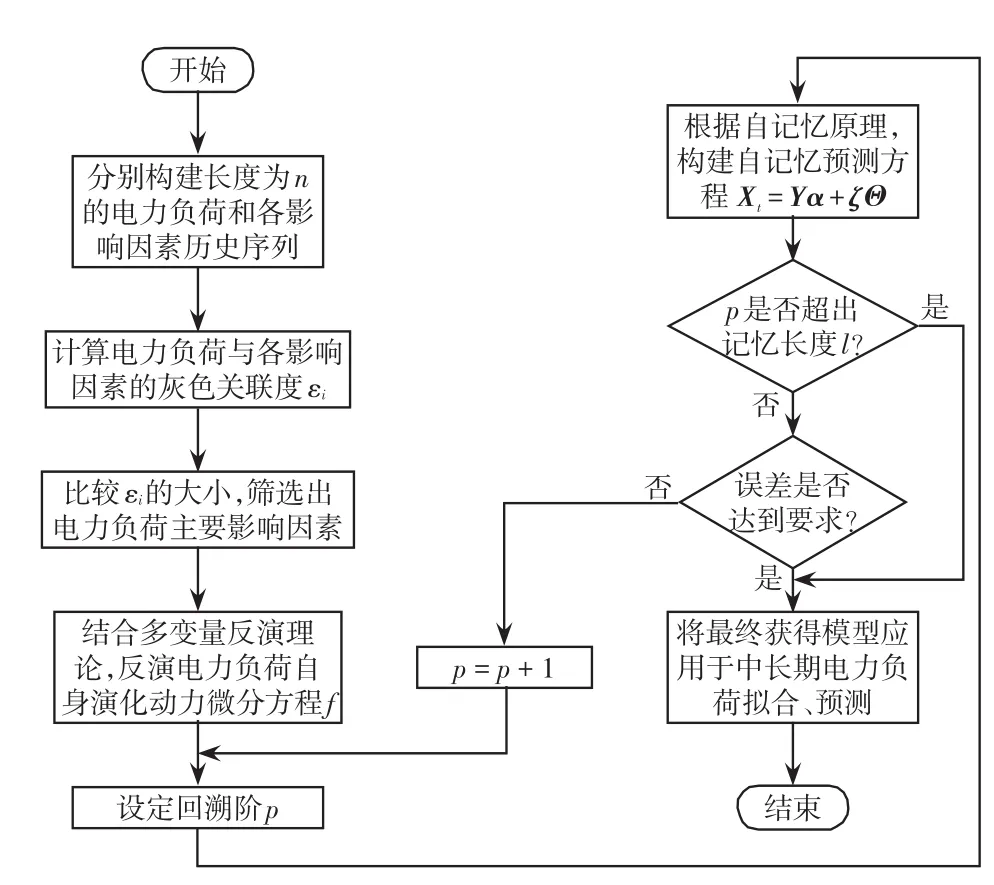
图1 基于多变量时间序列反演自记忆模型的中长期电力负荷预测流程Fig.1 Flow chart of mid-long term load forecasting based on multivariable time series inversion self-memory model
步骤5将反演得到的非线性方程作为电力负荷自身演化动力微分方程,结合自记忆原理,构建自记忆方程Xt=Yα+ζΘ,记忆系数矩阵α和Θ可使用最小二乘法求得,使用所得模型对一定时段历史数据进行拟合;
步骤6判断p是否超出记忆长度l,若是,则跳至步骤8,否则,跳至步骤7;
步骤7判断拟合误差是否达到要求,若是,则跳至步骤8,否则,取p=p+1,跳至步骤4;
步骤8将最终获得模型应用于中长期电力负荷拟合、预测;
步骤9结束。
3 算例分析
为了验证本算法应用到中长期电力负荷预测中的正确性和可靠性,本文利用某地区1978—2012年全社会用电量数据进行分析,本文算例的主要数据均来自于该地区2013年统计年鉴[20]。
3.1 记忆长度确定
根据第1.1节所述的电力负荷时间序列记忆性研究思路和方法,选取该地区1978—2012年全社会用电量时间序列进行记忆性研究,从而确定该序列的记忆长度。通过R S分析的统计量对原序列分析,以确定该序列的记忆长度,易得到该序列的图,具体见图2。

图2 电力负荷序列V(τ)vsln τFig.2 Power load time series ofV(τ)vsln τ
3.2 全社会用电量主要影响因素选取
为了能够确定该地区全社会用电量自身演化动力微分方程,需要从众多全社会用电量影响因素中筛选出主要影响因子。这里可根据第2.1节的灰关联分析法对影响因素进行主次区分。中长期电力负荷预测应考虑的影响因素主要有第一、二、三产业产值、人均GDP和人口等,以该地区1978—2012年上述影响因素实际数据为基础,使用灰色关联分析法分析全社会用电量和其影响因素之间的关联程度,找出影响全社会用电量变化的主要因素,结果如表1所示。

表1 全社会用电量和其影响因素之间的关联度Tab.1 Correlation degrees between total electricity consumption and its influencing factors
从表1可得,该地区全社会用电量与第二产业、人均GDP、人口、第三产业和第一产业的关联度依次递减,考虑到第一产业用电负荷较小,因此全社会用电量与第一产业产值关联度相对较小,这与实际情况相符。所以可选择第二、三产业产值、人均GDP和人口作为该地区全社会用电量主要影响因素。
3.3 非线性动力微分方程反演
以第3.2节结论为基础,反演全社会用电量动力微分方程,可假设该动力方程基本形式为
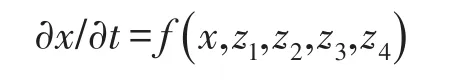
式中:x表示全社会用电量;z1、z2、z3和z4分别表示第二、三产业产值、人口和人均GDP。对于动力微分方程形式,可采用第2.2节所述具有一般性的非线性多项式,最高次幂设为2,可假设方程基本形式为
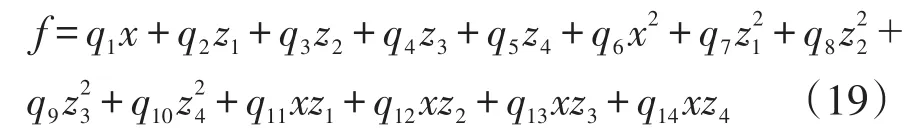
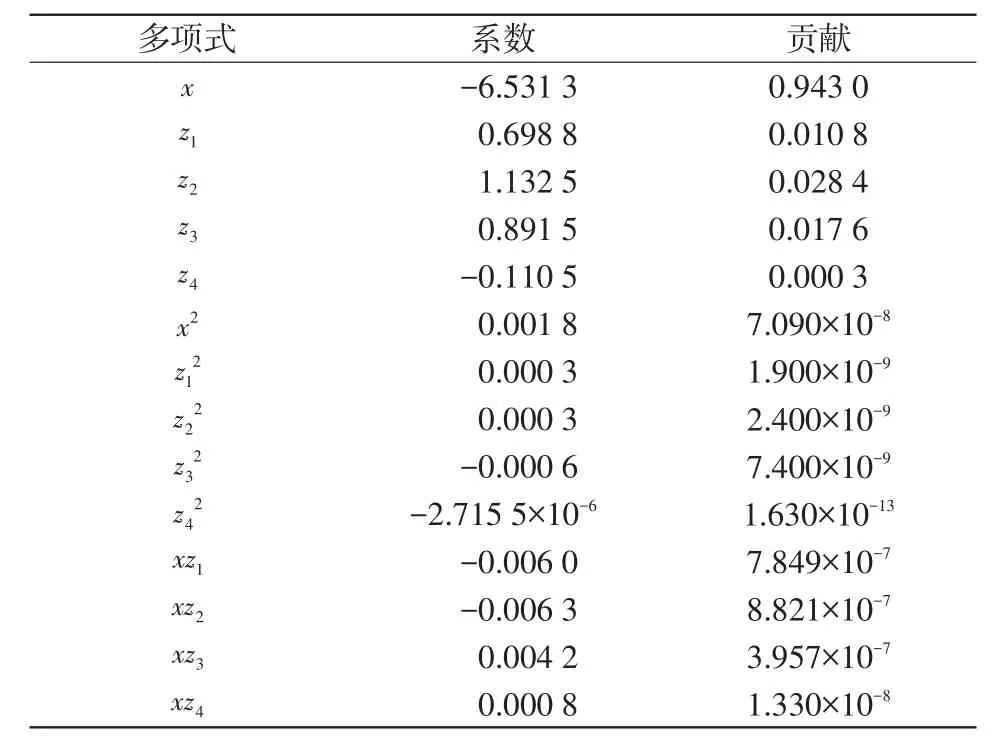
表2 多项式系数Tab.2 Multinomial coefficients
从表2可知,多项式x、z1、z2、z3和b4对方程影响较大,从而可得到全社会用电量动力微分方程为∂x∂t=-6.531 3x+0.698 8z1+1.132 5z2+0.891 5z3-0.110 5z4。
3.4 自记忆模型预测分析
得到动力微分方程式后,可构建自记忆预测模型,以1986—2002全社会用电量数据为基础,利用最小二乘法计算记忆系数,并将所得模型对2003—2006年全社会用电量进行预测验证。不妨设初始回溯阶p=1(1≤p≤34),并设定平均绝对值百分误差要求标准为MAPE≤5%,对原模型进行迭代计算。经计算可得到当p=7时,满足误差要求标准,求得此时记忆系数如表3所示。

表3 记忆系数Tab.3 Memory coefficients
将表3各参数代入式(16),对1986—2002年全社会用电量进行拟合。同时,为了验证该方法的可行性和有效性,从经典预测方法和现代预测方法中分别选取几种具有代表性的方法,并构建预测模型,进行对比分析。分别建立Logistic时间序列模型、偏最小二乘回归模型、等维新息灰色预测模型、基于遗传算法的BP神经网络模型和基于非线性回归的支持向量机模型。6种方法拟合结果如表4所示。6种方法拟合曲线如图3所示。其中,模型1为本文提出的基于多变量时间序列反演自记忆模型;模型2是Logistic时间序列模型;模型3是偏最小二乘回归模型;模型4是等维新息灰色预测模型;模型5是基于遗传算法的BP神经网络模型;模型6是基于非线性回归的支持向量机模型。
表4中模型1和模型4的参数均采用最小二乘法求解;模型2参数则采用Marquardt算法求解;模型3、模型5和模型6的内部参数均由模型自身内部算法求解。从表4和图3可见,模型1拟合的平均绝对值百分误差明显低于其他5个模型,达到0.42%,而且每年的拟合误差都在±1.5%之间,波动很小。

表4 6种预测模型全社会用电量拟合结果Tab.4 Fitting results of total electricity consumption by using six forecasting models
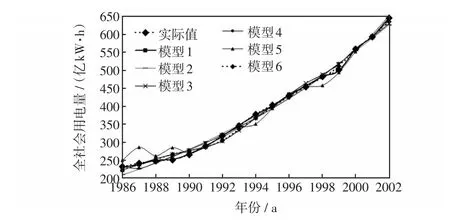
图3 6种方法的全社会用电量拟合曲线Fig.3 Fitting curves of total electricity consumption by using six methods
为了验证6种模型的预测效果,可利用上述通过拟合历史数据所得的6个全社会用电量预测模型对该地区2003—2006年全社会用电量进行预测,预测结果如表5所示。
本文提出的模型1以原始负荷数据为基础,通过反演计算获得模拟负荷演化过程的非线性动力微分方程,再结合自记忆原理进行建模。模型拟合值较实际值的平均拟合绝对值误差为0.42%,平均预测绝对值误差为2.75%,拟合与预测效果稳定,对于中长期负荷预测均为高精度。

表5 6种预测模型全社会用电量预测结果Tab.5 Forecasting results of total electricity consumption by using six forecasting models
模型2针对原始负荷数据采用Logistic时间序列模型建模,其拟合效果较好,平均拟合绝对值误差为2.83%,但是平均预测绝对值误差达到16.08%,表明该模型并不能准确模拟原始负荷序列未来变化趋势。
模型3采用偏最小二乘法进行建模,其平均拟合绝对值误差和平均预测绝对值误差分别为2.41%和4.44%,效果较好,一定程度上表明该模型能够较为有效地克服传统回归分析中的多重相关性问题,达到较好的预测效果。但是由于该模型未能考虑负荷自身变化规律,所以其预测精度很难再有提高。
模型5和模型6是现代人工智能预测技术的典型代表。模型5引入遗传算法对BP神经网络初始参数进行优化。模型6将支持向量机与非线性回归进行有机结合。模型5和模型6的拟合与预测效果都相对较好,但是人工智能算法往往都未能将负荷的记忆性纳入考虑,这使得历史值对预测值的影响并不能在模型中得以直观体现。
对比6种预测模型的预测结果可知:模型2仅仅使用Logistic模型来模拟原始负荷数列的变化过程,但实际负荷受到多方面因素的影响,未来负荷的变化趋势并不一定满足Logistic模型。因此,虽然模型2拟合效果较好,却具有较差的预测效果。模型4与模型2的拟合效果相近,但预测效果前者好于后者。模型4预测效果仍较差的主要原因是在使用新的预测值递补实际值时,预测得到的负荷与实际负荷的变化趋势存在一定的偏差,导致预测模型的精度降低。模型3相对于模型2、4预测效果有了较大的提升,主要原因是该模型考虑了多种因素对负荷的影响,并能有效克服传统回归分析中多重相关性的缺点。模型5、6和模型3的预测效果较为相近,但人工智能算法中一些参数的选取具有随机性,往往需要采用合适的智能寻优算法来迭代求解,这就大大增加了预测算法的复杂性。本文提出的模型1比其他5种算法的预测效果更好。该模型既考虑了负荷自身内在变化规律,也考虑了其他因素对负荷变化的影响,有效地提高了预测精度。综上所述,本文提出的方法相对于时间序列分析、回归分析、灰色理论、神经网络和支持向量机等预测模型均精度较高,具有较强的实用性和可行性。
4 结 论
(1)本文构建了用于中长期电力负荷预测的多变量时间序列反演自记忆模型。该方法以多变量反演理论为基础,结合自记忆原理,提出了基于主要影响因素的电力负荷多变量时间序列反演自记忆的建模原理与过程,该模型有效地提高了预测精度,为中长期负荷预测开创了一种新思路。
(2)本文方法能够很好地综合时间序列建模和传统回归建模的优势,既考虑了负荷自身变化规律,也考虑了其他因素对负荷变化的综合影响,对实际负荷预测工作有较强的借鉴意义。
(3)自记忆性原理包含有很多内容,其应用的方式也有很多种,如谱模式、随机-差分模式等,本文只是将其中涉及到时间序列的有关内容引入到电力负荷预测中,并做了初步应用,更深一步的应用还有待于以后的进一步研究。
[1]康重庆,夏清,刘梅.电力系统负荷预测[M].北京:中国电力出版社,2007.
[2]毛李帆,江岳春,姚建刚,等(Mao Lifan,Jiang Yuechun,Yao Jiangang,et al).采用正交信号修正法与偏最小二乘回归的中长期负荷预测(Medium and long term load forecasting based on orthogonal signal correction and partial least-squares regression)[J].中国电机工程学报(Proceedings of the CSEE),2009,29(16):82-88.
[3]毛李帆,江岳春,龙瑞华,等(Mao Lifan,Jiang Yuechun,Long Ruihua,et al).基于偏最小二乘回归分析的中长期电力负荷预测(Medium and long term load forecasting based on partial least squares regression analysis)[J].电网技术(Power System Technology),2008,32(19):71-77.
[4]马星河,闫炳耀,唐云峰,等(Ma Xinghe,Yan Bingyao,Tang Yunfeng,et al).基于优选组合预测技术的中长期负荷预测(Medium and long-term load forecasting based on optimized combination forecast technology)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2015,27(6):62-67.
[5]Mukherjee S,Osuna E,Girosi F.Nonlinear prediction of chaotic time series using support vector machines[C]//Neural Networks for Signal ProcessingⅦ.Amedia Island,USA,1997:511-520.
[6]Zhu Jiayuan,Ren Bo,Deng Hengxi,et al.Time series prediction via new support vector machines[C]//International Conference on Machine Learning and Cybernetics.Beijing,China,2002:364-366.
[7]张林,罗晓初,徐瑞林,等(Zhang Lin,Luo Xiaochu,Xu Ruilin,et al).基于时间序列的电力负荷预测新算法研究(Study on novel algorithm based on time series in power system load forecasting)[J].电网技术(Power System Technology),2006,30(S):595-599.
[8]李如琦,苏浩益,王宗耀,等(Li Ruqi,Su Haoyi,Wang Zongyao,et al).应用启发式最小二乘支持向量机的中长期电力负荷预测(Medium-and long-term load forecasting based on heuristic least square support vector machine)[J].电网技术(Power System Technology),2011,35(11):195-199.
[9]贺辉.电力负荷预测和负荷管理[M].北京:中国电力出版社,2012.
[10]王大鹏(Wang Dapeng).灰色预测模型及中长期电力负荷预测应用研究(Research on Grey Prediction Models and Their Applications in Medium-and Long-Term Power Load Forecasting)[D].武汉:华中科技大学电气与电子工程学院(Wuhan:College of Electrical&Electronic Engineering,Huazhong University of Science and Technology),2013.
[11]刘晓娟(Liu Xiaojuan).基于智能方法的电力系统负荷预测模型及其应用研究(Intelligent Method Based Load Forecasting Models and Application Research in Power System)[D].上海:东华大学信息科学与技术学院(Shanghai:School of Information Science and Technology,Donghua University),2013.
[12]王大鹏,汪秉文(Wang Dapeng,Wang Bingwen).基于变权缓冲灰色模型的中长期负荷预测(Medium-and longterm load forecasting based on variable weights buffer grey model)[J].电网技术(Power System Technology),2013,37(1):167-171.
[13]曹鸿兴.动力系统自记忆原理——预报与计算应用[M].北京:地质出版社,2002.
[14]徐绪松,马莉莉,陈彦斌(Xu Xusong,Ma Lili,Chen Yanbin).R/S分析的理论基础:分数布朗运动(Theoretical basis of R/S analysis:fractional Brownian motion)[J].武汉大学学报:理学版(Journal of Wuhan University:Natural Science Edition),2004,50(5):547-550.
[15]张晓伟(Zhang Xiaowei).水文动力系统自记忆特性及其应用研究(Study on Self-Memory Characteristics of Hydrology Dynamic System and Its Application)[D].西安:西安理工大学水利水电学院(Xi'an:Institute of Water Resources and Hydro-Electric Engineering,Xi'an University of Technology),2009.
[16]康重庆,夏清,张伯明(Kang Chongqing,Xia Qing,Zhang Boming).电力系统负荷预测研究综述与发展方向的探讨(Review of power system load forecasting and its development)[J].电力系统自动化(Automation of Electric Power Systems),2004,28(17):1-11.
[17]毛李帆(Mao Lifan).电网规划中长期负荷预测技术的研究(Research on Technique of Medium and Long Term Load Forecasting for Power Grid Planning)[D].长沙:湖南大学电气与信息工程学院(Changsha:College of Electrical and Information Engineering,Hunan University),2011.
[18]朱继萍(Zhu Jiping).长期电力负荷预测及相关因素不确定性的影响(Long-term Load Forecasting and Effects of Uncertainty in Related Elements)[D].西安:西安科技大学通信与信息工程学院(Xi'an:School of Communication Engineering,Xi'an University of Science and Technology),2005.
[19]侯勇,张荣乾,谭忠富,等(Hou Yong,Zhang Rongqian,Tan Zhongfu,et al).基于模糊聚类和灰色理论的各行业与全社会用电量关联分析(Correlative analysis of power consumption for various industries to whole society based on fuzzy clustering and grey theory)[J].电网技术(Power System Technology),2006,30(2):46-50.
[20]王建平,马俊贤.上海统计年鉴-2013[M].北京:中国统计出版社,2013.
Mid-long Term Power Load Forecasting Based on Multivariable Time Series Inversion Self-memory Model
ZOU Pinjing,YAO Jiangang,KONG Weihui,HU Linbo,PAN Xueqing
(College of Electrical and Information Engineering,Hunan University,Changsha 410082,China)
Due to the complication and nonlinearity of power load forecasting,it is difficult to obtain accurate results by using the traditional mid-long term forecasting model.To improve the forecasting accuracy,a multivariable time series inversion self-memory model is constructed.The proposed model uses grey correlation analysis to select the main influencing factors of the power load,and adopt them to perform the dynamic equation inversion for the variation of power load.Moreover,the fitting and forecasting of power load is realized by combining the self-memory model.In this way,the forecasting precision is improved and the forecasting results can reflect the inherent variation characteristics of historical power load data to the maximum extent,which improves the stability of fitting and forecasting.To verify the effectiveness of the proposed model,the total electricity consumption data in a certain region from 1986 to 2002 are used as training samples to conduct fitting analysis,and further forecast the total electricity consumption in years 2003-2006.The fitting and forecasting results prove the validity and feasibility of the proposed model in the mid-long term power load forecasting.
mid-long term power load forecasting;grey correlation analysis;main influencing factor;dynamic equation inversion;self-memory model
TM734
A
1003-8930(2017)10-0098-08
10.3969/j.issn.1003-8930.2017.10.017
2016-01-20;
2017-07-03
邹品晶(1992—),男,硕士研究生,研究方向为电力系统负荷预测及电网规划。Email:848468385@qq.com
姚建刚(1952—),男,硕士,教授,博士生导师,研究方向为电力市场、智能电网及高压外绝缘。Email:yjg_hnu@126.com
孔维辉(1991—),男,硕士研究生,研究方向为电力系统负荷预测及电网规划。Email:3175669024@qq.com
