含分布式电源及电动汽车的多代理配电网重构

刘思聪，周步祥，彭章刚，唐 浩，邓苏娟

（四川大学电气信息学院，成都 610065）

含分布式电源及电动汽车的多代理配电网重构

刘思聪，周步祥，彭章刚，唐 浩，邓苏娟

（四川大学电气信息学院，成都 610065）

为缓解分布式电源和电动汽车的接入对配电网电能质量和网络损耗的影响，并谋求配电网重构时电能质量和网络损耗的最优控制，本文提出一种基于JADE开发平台下的多代理控制系统，在配电网重构过程中充分考虑分布式电源和电动汽车对配电网潮流影响。在改进的IEEE-33节点系统中进行了仿真分析。仿真结果与传统局部控制策略相比较，既有效解决了馈线过载和电压越限问题，又优化了配电网电能质量和网络损耗，并具有更强的鲁棒性和可靠性。

多代理控制系统；配电网重构；分布式电源；电动汽车；最优控制

日益增长的电能需求使得馈线过载和电压越限等一系列问题发生的频率越来越高。并且由于分布式电源DG（distributed generation）的高渗透率以及电动汽车EV（electric vehicle）的普及，使得在进行配电网重构时有必要考虑这些因素的影响。

文献[1]提出了一种改进的生物地理学优化算法来进行重构。文献[2]针对重构设计了一种改进免疫算法。文献[3]则提出了一种改进蚁群算法来解决重构问题。文献[1，3]对于配电网重构的研究均集中在优化算法上，并没有针对重构的控制方法做进一步研究。文献[4]针对配电网提出了一种分时段的多代理重构方案。文献[5-6]设计了一种多代理故障恢复模型。文献[7]针对舰船电力系统提出了一种多代理系统重构方案。上述文献均没将多代理技术应用到城市配电网重构中，也并没考虑DG和EV的接入对配电网重构的影响。

传统重构的方法一般分为集中控制和分散控制。集中控制是利用一个或者多个控制中心来制定全局最优的重构方案。而分散控制则没有控制中心，因此很难实现全局的最优处理，但其鲁棒很好。在传统局部控制方法下，配电网DG单元的整合会严重影响系统的电压水平，造成过压或者欠压，导致系统损耗增加，同时还会影响有载调压变压器ULTC（under load tap changer）和并联电容器[8-11]。

本文提出了一种混合集中控制和分散控制的多代理控制系统MACS（multi-agent control system），建立了系统网损最小和电压偏移最小的多目标重构模型，并利用模糊集理论将多目标优化转化为单一目标优化，采用本文提出的MACS进行重构决策。

1 含有DG的配电网的电压控制问题

限制提高DG渗透率的主要因素有：馈线流量限制、保护问题以及电压升高问题。处理电压升高问题有如下3种方法。第1种方法：DG注入网络的无功由连接的电力电子设备来控制。但由于DG的容量是固定的，增加无功的注入会减少有功的注入，这降低了DG的经济收益。因此这个方法的花费太大。只有在使用电压控制设备后仍然不能调整电压到规定范围的情况下，才能使用这种方法。第2种方法：只用电压控制设备来规范系统电压。在满足式（1）的情况下，电压调节器能够调节所有馈线的最大电压和最小电压；如果不满足式（1），电压调节器就不能消除整个系统的电压越限，则采用第3种方法—配电网重构。

式中：Vmax和Vmin分别为配电网节点电压的最大值和最小值；Vmax，allow和Vmin，allow分别为配电网允许的最大电压和允许的最小电压。

假设馈线A有N个负荷节点，馈线B有M个负荷节点，如图1所示。则馈线A的节点I-1的节点电压为

式中：VI-1（0）和VI-1（1）分别为节点I-1 负荷转移前的电压和负荷转移后的电压；ΔPL和ΔQL分别为转移负荷总共的有功和无功。

馈线B的节点J的节点电压为

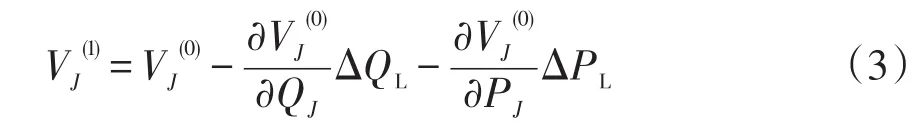
式中，VJ（0）和VJ（1）分别为节点J负荷转移前的电压和负荷转移后的电压。

图1 负荷转移示意Fig.1 Schematic of load transfer

2 含DG以及EV负荷的配电网动态重构数学模型

以往提出的配电网重构虽然顾及了EV的接入对电网的影响，但只建立了较为简单的数学模型。由于科技的快速发展，在未来的配电网中将会大量接入类似EV这样的新型负荷。本文提出了考虑DG以及EV负荷同时接入时的配电网重构数学模型，这符合未来电网发展趋势。

2.1 EV的接入模型

2.1.1 传统EV接入模型

本文采用文献[1]提出的传统EV模型。假设各台EV开始充电的时刻的概率密度函数[12]为

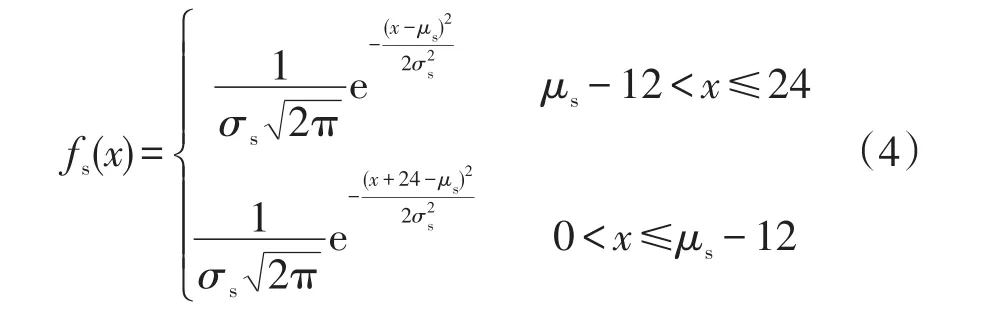
式中：x为每台EV的充电功率，kW；μs=17.6；σs=3.4。

假设EV的充电功率服从均匀分布，则其概率密度函数为

假设TC为充电时长，并设其概率密度函数为

式中：μD=3.2；σD=0.88；x＞0。设为EV在t0时刻的充电状态，表示正在充电，表示未在充电，其概率函数可表示为

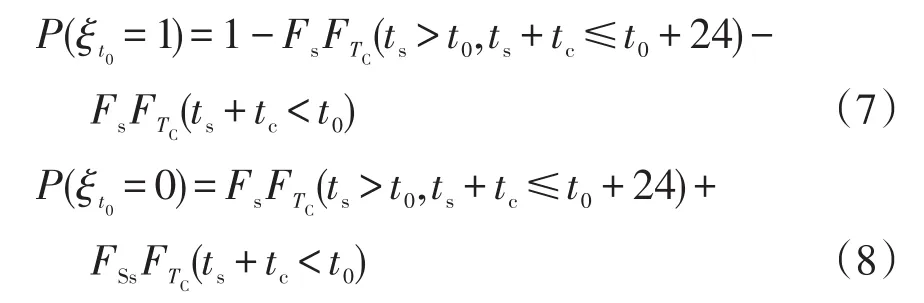
式中：ts为开始充电的时刻；tc为充电时长；Fs为充电起始时刻的概率分布函数；FTC为充电时长的概率分布函数。

2.1.2 V2G接入模型

削峰填谷是智能电网所追求的一个目标。因此本文引入文献[13]提出的V2G（vehicle to grid）模型。设家庭汽车的日里程概率密度函数为

设电动汽车起始电荷状态SOC0为

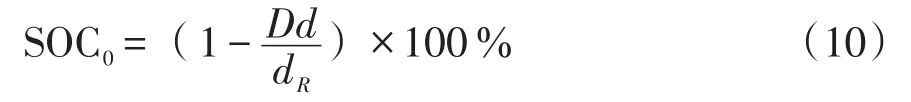
式中：D为行驶天数；d为日行驶里程；dR为电动汽车的最大行驶路程。

充、放电持续时间tc和tf分别为

式中：SOCc和SOCd分别为电池充电和放电的最终状态，并且SOCd的最小值为0.1；rci和rdi分别为充电电流和放电电流。

2.2 DG的接入模型

2.2.1 风力发电接入模型

风力发电机的出力受到风速的影响，而风速的预测随机性很大[14]。本文采用Weibull分布函数来近似作为风速的概率分布，并用线性分段函数来描述风力发电机的出力。

设f（v）表示风速的概率密度函数，PW表示风力发电机的出力，则有

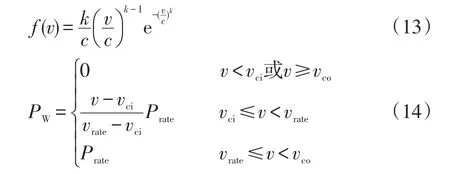
式中：v为风力发电机风速；k和c分别为形状参数和尺度参数；Prate为风力机的额定容量；vci、vrate、vco分别为切入风速、额定风速以及切出风速。

2.2.2 光伏发电接入模型

本文采用Beta分布函数来描述太阳光照的概率分布。

设f（r）为光照强度的概率密度函数，PM表示光伏发电机的出力，则有

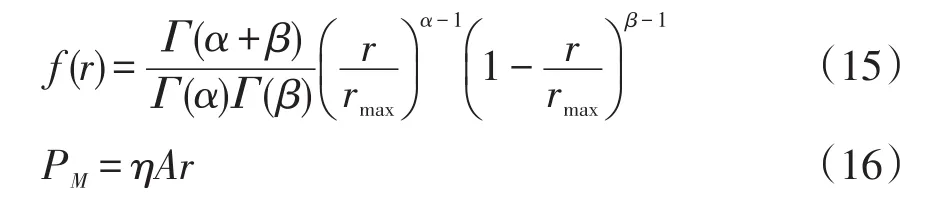
式中：r和rmax分别为某一段时间内的光照强度和其最大值；α、β为Beta分布的形状参数；A为光伏电板的面积；η为光-电转换效应。

2.3 配电网重构模型

本文以重构后网损最小以及电压偏移最小为综合指标建立目标函数，运用模糊集理论将多目标转化为单一目标得到最终的目标函数。

2.3.1 目标函数

网损最小目标函数为

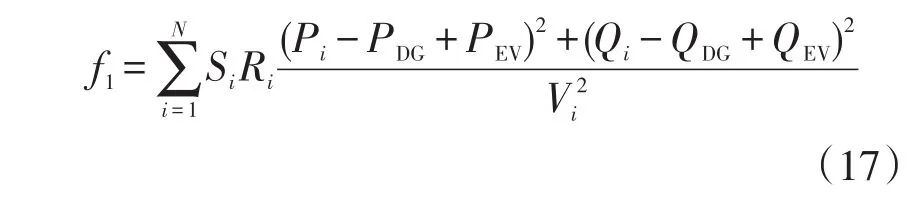
式中：Si为开关i的状态，Si=1表示开关i闭合，Si=0表示开关i断开；Ri为支路i的电阻；Pi和Qi分别为支路i的有功功率和无功功率；PDG和QDG分别为DG注入有功功率和无功功率；PEV和QEV分别为电动汽车注入的有功功率和无功功率（这里将电动汽车当做出力为负的DG处理）；Vi为支路i末端的节点电压；N为支路总数。

电压偏移最小目标函数为

式中：Vi为节点i的电压；Vi，spec为节点i的期望电压；ΔVi，max为节点i的最大允许偏差；Nb为节点数。

本文利用模糊集理论将多目标优化问题转化为单一目标优化问题。每个子目标的模糊隶属度函数μi为

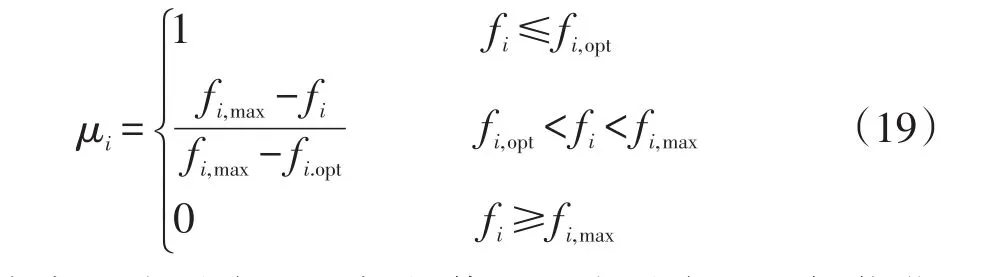
式中：fi为对应子目标的值；fi，opt为对应子目标优化后的最佳取值；fi，max为对应子目标的最大取值。

设模糊化后的单一目为λ，则有

式中，λ表示总体满意度。

2.3.2 约束条件

配电网重构的约束条件包括潮流约束方程、节点电压约束、传输功率约束以及网络拓扑约束等。同时本文还需要考虑风力发电、光伏发电以及充电站接入点的功率因数约束。

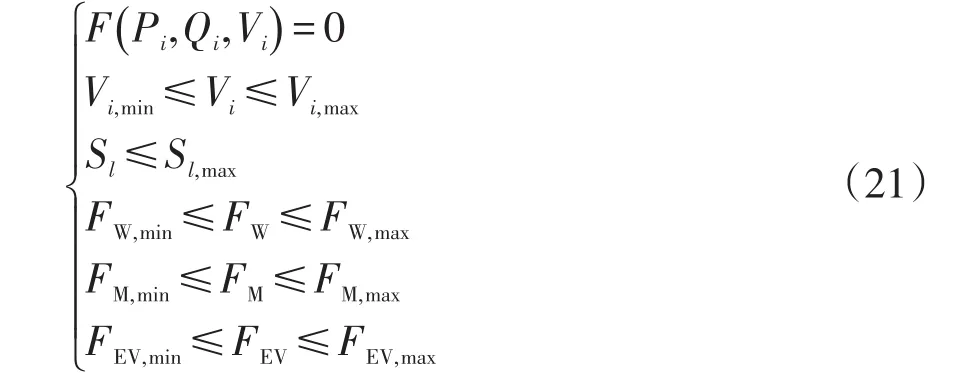
式中：Pi、Qi、Vi分别为节点i的有功功率、无功功率、节点电压；Vi，max和Vi，min分别为节点i电压的上限和下限；Sl和Sl，max分别为支路l的传输功率以及传输功率的上限；FW、FW，max和FW，min分别为风力发电功率及其功率上、下限；FM、FM，max、FM，min分别为光伏发电功率及其功率上、下限；FEV、FEV，max、FEV，min分别为EV充电站的功率及其功率上、下限。

本文采用牛顿-拉夫逊算法来进行潮流计算。

3 多代理控制系统及其基本原理

本文提出的MACS的工作流程如图2所示。它由负荷代理 LA（load agent）、馈线代理FA（feeder agent）和调节器代理RA（regulator agent）3 部分组成。SR和SR，max分别为配电变压器潮流及其最大值；tap、tapmax、tapmin分别为配电变压器变比及其最大、最小值；Vprim和Vsec分别为配电变压器的一次侧和二次侧电压；IRPSC为要求增加RPS的LA的数目；DRPSC为要求减少RPS的LA的数目。

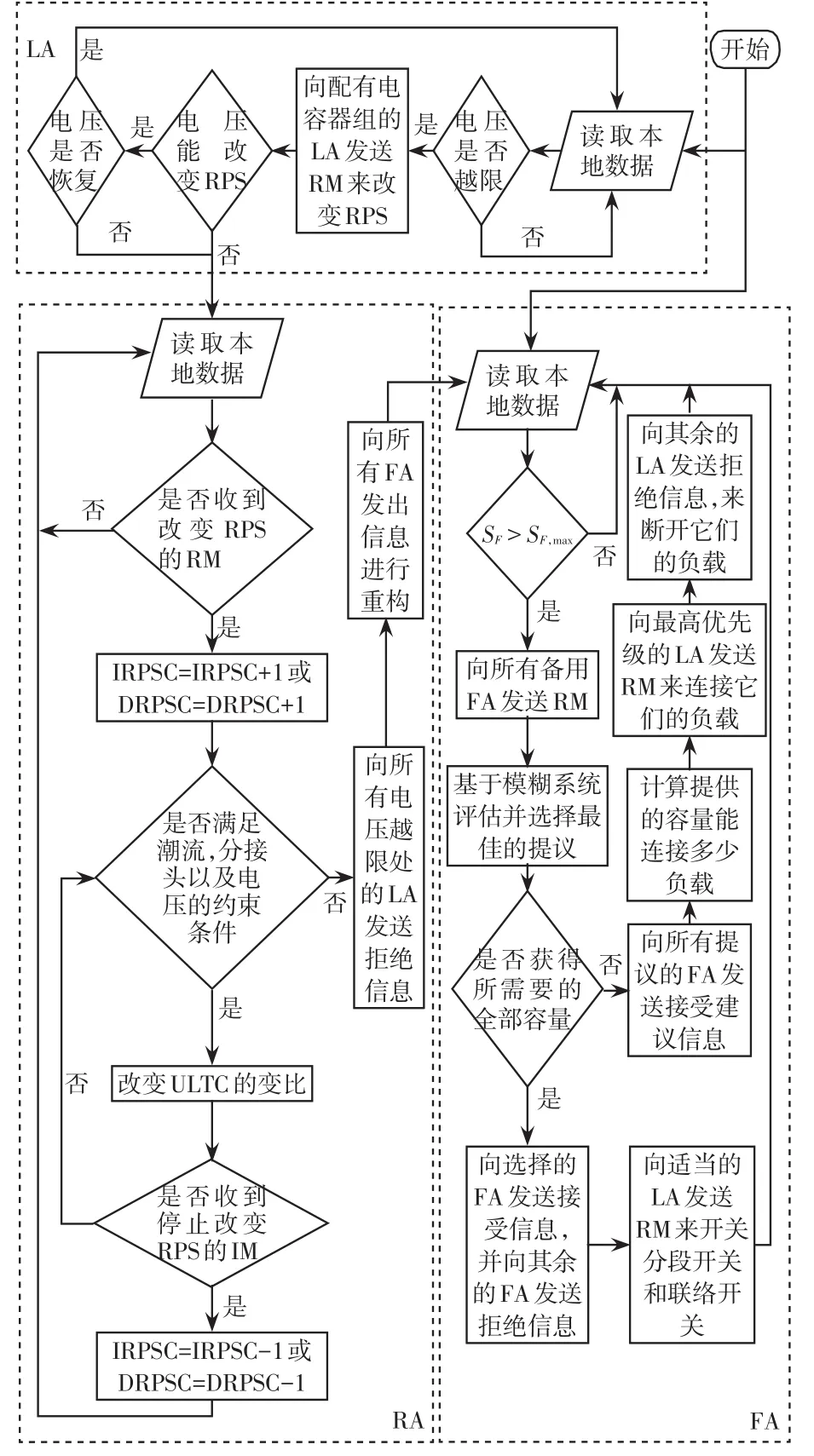
图2 代理工作流程Fig.2 Flow chart of behavior of agent

3.1 负荷代理

每根馈线有多个LA，LA负责监控连接线路的节点，电容器组的状态以及DG单元的状态。具体任务如下。

（1）每个LA监控自己节点的负载功率、电压、上端以及下端潮流。

（2）假设LA1检测到电压越限。如果该节点配有无功补偿器（电容器组），它会优先选择在本地实施电压校正。

（3）如果LA1没有配备无功补偿器，它会通过其馈线上的FA向自己馈线上或者相邻馈线上配有开关电容器组的LA发送需求信息RM（requirement message）来进行无功补偿。

（4）接收到RM的LA检查其可用的无功补偿容量并向LA1发送接受信息或者拒绝信息。

（5）如果此LA达到容量上限，或者相邻线路的潮流达到上限，或者电容器组开关操作次数达到每日最大次数，或者它自己的节点也发生了电压越限，那么它会向LA1发送拒绝信息。

（6）LA1会向RA发送RM来进行无功补偿。

（7）RA检查其可用容量并向LA1发送接受信息或者拒绝信息。

（8）如果RA达到容量上限，或者潮流超过限制，或者它的二次侧电压越限，那么它会向LA1发送拒绝信息。

3.2 馈线代理

每根馈线有一个单独的馈线代理FA，FA负责监控馈线的潮流。其具体任务分别从以下两种情况下说明。

3.2.1 系统过载

在系统过载情况下，FA的任务如下。

（1）假设FA1检测到它的馈线潮流超过限制，它会向所有相邻的FA发送RM来转移一部分负荷。

（2）如果这些FA有多余的备用容量，那么它们会向FA1发送接受信息。否则发送拒绝信息。

（3）FA1收到所有回复信息后，会基于模糊逻辑算法选择最佳的方案并向其发送接受信息，向其余FA发送拒绝信息。

（4）FA1向配有联络开关的LA发送指令去连接它选择的FA。

（5）当提供给FA1的容量总和仍然不足以消除过载时，FA1会向所有提供能量的FA发送接受信息。这些FA会基于负荷的优先级来确定负荷转移的数量。

3.2.2 电压越限

在电压越限情况下，FA的具体任务如下。

（1）假设FA1从RA收到一个让它做出重构的信息，它会向LA发送信息来收集节点电压和负载功率的数据，为重构做准备。

（2）FA1会根据式（2）来判断需要转移的负荷，并向相邻的FA发送RM来转移这些负荷。

（3）当相邻的FA还有多余容量时，它会根据式（3）来确定可以提供的容量，并向FA1发送信息。

（4）FA1基于模糊算法选择最佳建议。

（5）当FA1总共收到的容量仍然不足时，它会向所有FA发出接受建议信息。

3.3 调节器代理

RA负责检测它节点的一次侧电压和二次侧电压以及配电变压器的潮流。其具体任务如下。

（1）当RA收到要求无功补偿的信息时，它会检测它的备用容量以及一次和二次侧电压水平并向LA回复接受或者拒绝信息。

（2）如果RA既收到要求增加无功的信息，又收到要求减少无功的信息。它会向所有LA发送拒绝信息并向所有FA发送信息来进行重构。

（3）如果ULTC变比达到极限，或者潮流达到最大限制，或者分接头动作次数达到每日最大允许次数，那么RA会向所有电压越线处的LA发送拒绝信息，然后停止分接头的动作，并向FA发送信息来进行重构。

（4）如果RA收到让它停止改变无功的信息，那么它会停止改变分接头。

3.4 馈线建议的评估与选择

在重构过程期间，有关的FA必须把馈线提供的建议进行排序，并利用模糊系统做出决策。本文用到的模糊系统有两个输入：提供的能量（PP）以及提供者的距离（PD）。第1个输入（PP）有3个模糊集，分别是低（L）、中（M）、高（H）。第2个输入（PD）有2个模糊集，分别是低（L）和高（H）。模糊系统只有优先选择指数（SPI）这一个输出。输出（SPI）有6个模糊集，分别是非常高（VH）、高（H）、中（M）、低（L）、非常低（VL）和极低（VVL）。图3为输入和输出的隶属函数。表1为输入和输出的模糊规则。本文用质心法来逆模糊化，以便在模糊系统中得到SPI的精确值。图4描述了在不同输入的情况下SPI的变化。

由于本文提出的控制方案依靠通信系统，并且对于大规模的电网而言，有关的FA会从不同长度的路径上收到大量不同的电力参数建议。这些FA需要评估并选择最佳的建议。但由于相邻馈线提供的能量是变化的，因此这项工作没有预先固定好的优先级列表。这也就是说，SPI与两个输入量的数学关系没有明确的定义。因此，使用模糊逻辑来处理这个问题是可行的。

图3 PD、PP以及SPI的模糊隶属度函数Fig.3 Fuzzy membership functions of PD，PP and SPI

表1 模糊规则Tab.1 Fuzzy rules

图4 不同输入下的SPI变化Fig.4 Variation of SPI with different inputs

4 算例分析

用JADE作为多代理方案的开发平台。用MATLAB/PSAT来模拟电力系统。用数据代理来连接MATLAB和JADE。这种数据代理是包含不同数据结构的JAVA对象。主要的两个数据代理是获得地址代理和设置地址代理，分别用来读取电力系统地址和设置电力系统的控制动作。在时域仿真过程中，电力系统运行条件下的信息都是通过数据代理，从MATLAB环境下传输到JADE环境下。并且在JADE环境下的代理（LA、FA、RA）会处理这些信息，如果需要的话，产生控制动作，把控制动作的信息放入数据代理中，再传输到MATLAB环境下。图5是在仿真模型下阐述PSAT-MATLAB-JADE的整合原理。算例研究采用改进的IEEE33节点配电网来评估本文提出的MACS。图6为改进后的IEEE33节点测试配电网，它有32个分段支路以及5个联络开关，额定电压是12.66 kV，系统总负载为3.72 MW和2.3 Mvar，所有的分段开关的初始状态是闭合的，所有的联络开关初始状态是断开的，馈线1的载流量是400 A（5.064 MV·A），其他馈线的载流量是200 A（2.53 MV·A）。4个FA间的距离由表2给出。

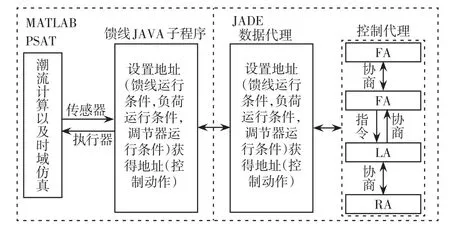
图5 PSAT-MATLAB-JADE并联运行示意Fig.5 Schematic of PSAT-MATLAB-JADE under parallel operation

图6 改进后的IEEE 33节点配电系统Fig.6 Modified IEEE 33-node distribution system

表2 各FA间的距离Tab.2 Distances between different FAs

对测试配电网做以下的修改。

（1）配电变压器配备ULTC（分接头范围为±10%，分接头动作的时间延迟为5 s，分接头的初始位置在0接头处）。

（2）DG单元分别被安装在：第32节点（DG1），第22节点（DG2）。且DG1为风力发电，DG2为光伏发电，每个DG单元的额定容量为1 MW，DG在各时段出力的变化如图7所示。

（3）开关电容器组安装在第13节点和第31节点。每一个电容器组的额定容量为1 Mvar。

（4）电动汽车站接在第16、17节点，且假设每个汽车站有1 000台电动汽车，每台电动汽车额定功率为1 kW，且EV1为V2G模型，EV2为一般模型。所有电动汽车在一天内各时段的用电需求如图7所示。

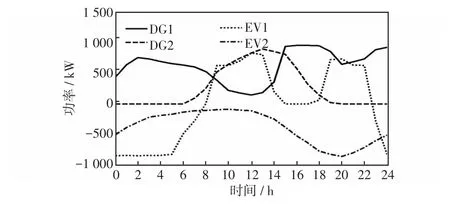
图7 各时段DG出力以及EV功率Fig.7 Output power of different DGs and powers of EVs

普通负荷功率参考某地区某日负荷特性曲线。算例采用文献[2]提出的改进免疫算法求解最优重构方案。种群数目、选择细胞数量以及克隆倍数分别设置为50、10、20，迭代精度设定为10×1012。算例对比了传统的局部控制下的重构和本文提出的MACS重构下的电压偏移以及网损。

图8为在不同时刻采用不同控制方案下的电压偏差，这里的电压偏差由式（18）确定。图9为采用不同控制方案下各时段的网络损耗。

图8 各时刻电压偏差Fig.8 Hourly voltage deviations

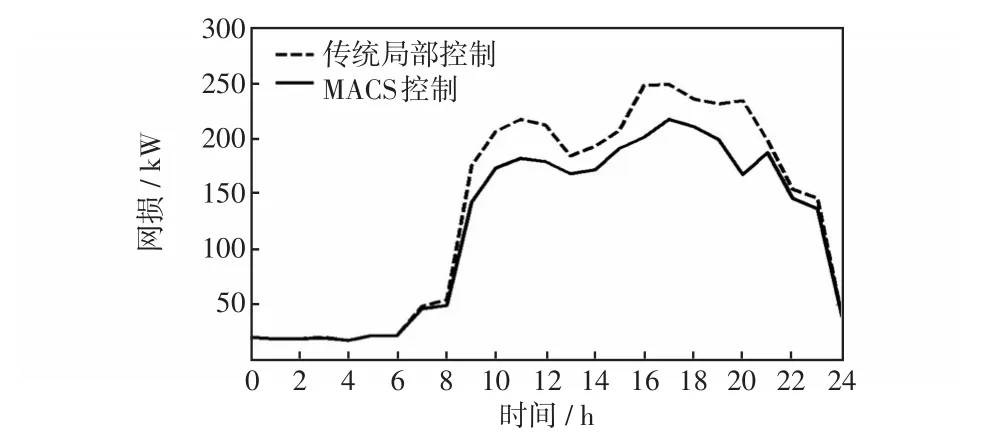
图9 各时刻网损Fig.9 Hourly network loss

通过图8可以看出采用MACS方案下的不同时刻的电压偏差相比较采用传统局部控制方案下的电压偏差更小，这是由于MACS中具有协调控制无功补偿器的机制，并且RA也会进行相应的无功补偿。同时，在满足式（1）的条件下，系统能够自动进行无功补偿，从而避免了DG单元不必要的有功缩减以及配电网的重构动作，减少了系统花费。从图9可以看出，与传统控制方案相比，在MACS方案下，系统各时段网络损耗也相对更小。

5 结 语

本文通过JADE开发平台并利用多代理控制技术，设计了一种混合集中式和分散式的多代理控制重构系统。并通过改进的IEEE33节点系统模拟了接入分布式电源和电动汽车时的配电网重构。仿真结果表明本文提出的多代理控制系统相较于传统的局部控制系统具有更强鲁棒性。由于RA工作机制，使得此多代理控制系统能够全面地解决电压越限和馈线过载，避免了传统分散式控制的弊端。同时由于具有协调无功补偿器的机制，此多代理控制系统还能避免DG单元不必要的有功缩减。

[1]朱正，廖清芬，刘涤尘，等（Zhu Zheng，Liao Qingfen，Liu Dichen，et al）.考虑新能源与电动汽车接入下的主动配电网重构策略（Strategy of distribution network reconfiguration considering wind power and electric vehicle integration）[J].电力系统自动化（Automation of Electric Power Systems），2015，39（14）：82-88，96.

[2]刘畅，黄民翔（Liu Chang，Huang Minxiang）.含多种分布式电源的配电网重构优化研究（Distribution network reconfiguration with a variety of DGs）[J].电力系统保护与控制（Power System Protection and Control），2013，41（6）：13-18.

[3]李奔，刘会家，李珺（Li Ben，Liu Huijia，Li Jun）.考虑网络结构优化的含风电配电网多目标重构（Multi-objective reconfiguration of distribution network with wind power generators considering network survivability）[J].电力系统保护与控制（Power System Protection and Control），2015，43（17）：57-62.

[4]李振坤，陈星莺，赵波，等（Li Zhenkun，Chen Xingying，Zhao Bo，et al）.配电网动态重构的多代理协调优化方法（Dynamic reconfiguration of the distribution network based on multi-agent systems）[J].中国电机工程学报（Proceedings of the CSEE），2008，28（34）：72-79.

[5]丁施尹，刘明波，谢敏，等（Ding Shiyin，Liu Mingbo，Xie Min，et al）.应用多代理技术求解高压配电网故障恢复问题（Amulti-agentapproachtofaultrestorationinhighvoltage distribution networks）[J].电力系统保护与控制（Power System Protection and Control），2012，40（9）：54-61.

[6]李红伟，孔冰，李超（Li Hongwei，Kong Bing，Li Chao）.基于网损最小的配电网多代理复电系统设计（Design of multi-agent distribution network restoration system based on minimum grid loss）[J].电力自动化设备（Electric Power Automation Equipment），2014，34（4）：155-161.

[7]黎恒烜，孙海顺，文劲宇，等（Li Hengxuan，Sun Haishun，Wen Jinyu，et al）.用于舰船电力系统重构的多代理系统设计（Design of a multi-agent system for shipboard power system reconfiguration）[J].中国电机工程学报（Proceedings of the CSEE），2011，31（10）：81-87.

[8]陈武，段斌（Chen Wu，Duan Bin）.变电站智能电子设备动态重构闭锁逻辑生成多代理系统（A multi-agent system for interlocking logic generation in dynamic reconfiguration of intelligent devices in substations）[J].电力系统自动化（Automation of Electric Power Systems），2015，39（21）：107-112.

[9]赵晶晶，李新，彭怡，等（Zhao Jingjing，Li Xin，Peng Yi，et al）.基于粒子群优化算法的配电网重构和分布式电源注入功率综合优化算法（A comprehensive optimization algorithm for injection power of distributed generation and distribution network reconfiguration based on particle swarm optimization）[J].电网技术（Power System Technology），2009，33（17）：162-166.

[10]蔡国伟，杜毅，李春山，等（Cai Guowei，Du Yi，Li Chunshan，et al）.基于支持向量机的中长期日负荷曲线预测（Middle and long-term daily load curve forecasting based on support vector machine）[J].电网技术（Power System Technology），2006，30（23）：56-60.

[11]李传健，刘前进（Li Chuanjian，Liu Qianjin）.考虑风力发电随机性的配电网重构（Distribution network reconfiguration considering randomness of wind power generation）[J].电力系统自动化（Automation of Electric Power Systems），2010，34（20）：34-39.

[12]田立亭，史双龙，贾卓（Tian Liting，Shi Shuanglong，Jia Zhuo）.电动汽车充电功率需求的统计学建模方法（A statistical model for charging power demand of electric vehicles）[J].电网技术（Power System Technology），2010，34（11）：126-130.

[13]艾圣芳，林湘宁，万云飞，等（Ai Shengfang，Lin Xiangning，Wan Yunfei，et al）.考虑V2G 模式的含多个电动汽车充电站有源配电网规划研究（Study of the active distribution network planning considering multiple electric vehicle charging stations participating in V2G applications）[J].中国电机工程学报（Proceedings of the CSEE），2013，33（34）：122-129.

[14]陈亚博，盛戈皞，黎建，等（Chen Yabo，Sheng Gehao，Li Jian，et al）.含光伏和风电的电力系统随机生产模拟（Probabilistic production simulation of power system with photovoltaic power and wind power）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2015，27（5）：1-6.

Reconfiguration of Distribution Network with Distributed Generations and Electric Vehicles Using Multi-agent

LIU Sicong，ZHOU Buxiang，PENG Zhanggang，TANG Hao，DENG Sujuan
（School of Electrical Engineering and Information，Sichuan University，Chengdu 610065，China）

In order to alleviate the influence of the access of distributed generations and electric vehicles on the power quality and network loss of distribution network，and to seek the optimal control of power quality and network loss in the reconfiguration of distribution network，a multi-agent control system is proposed based on JADE development platform in this paper，which fully considers the impact of distributed generations and electric vehicles on the power flow therein.Simulation analysis is carried out in a modified IEEE 33-node system.Compared with the traditional local control strategy，the multi-agent control system is more effective in solving the problems such as feeders’congestion and overlimit voltage.Moreover，it optimizes the power quality and network loss，showing stronger robustness and reliability.

multi-agent control system（MACS）；reconfiguration of distribution network；distributed generation（DG）；electric vehicle（EV）；optimal control

TM762

A

1003-8930（2017）10-0091-07

10.3969/j.issn.1003-8930.2017.10.016

2016-03-28；

2017-07-04

刘思聪（1993—），男，硕士研究生，研究方向为电力系统稳定与控制、调度自动化及计算机信息处理。Email：liusicong97@outlook.com

周步祥（1965—），男，博士，教授，研究方向为电力系统电网规划、调度自动化及计算机信息处理。Email：hiway_scu@126.com

彭章刚（1990—），男，硕士研究生，研究方向为电力系统稳定与控制、调度自动化及计算机信息处理。Email：pengswpu@163.com