不接地系统高阻接地故障特征及选线适用性分析

潘本仁，管廷龙，桂小智，薛永端，郭 亮

（1.国网江西省电力公司电力科学研究院，南昌 330096；2.中国石油大学（华东）信息与控制工程学院，青岛 266580）

不接地系统高阻接地故障特征及选线适用性分析

潘本仁1，管廷龙2，桂小智1，薛永端2，郭 亮1

（1.国网江西省电力公司电力科学研究院，南昌 330096；2.中国石油大学（华东）信息与控制工程学院，青岛 266580）

在不接地系统中，相比于低阻接地故障，高阻接地故障电流更小，故障点更不稳定，故障选线难度更大。基于故障等值电路，分析了不接地系统高阻接地故障工频及暂态电流特征，并对故障与健全出线的故障工频及暂态电气量进行了比较。得到了故障电流随不同故障条件（过渡电阻、线路电感、系统对地电容、故障初始相角）的变化规律。证明了现有常用的暂态电流幅值比较、极性比较以及暂态功率方向判别等选线方法仍适用于不接地系统高阻接地故障。若借助故障工频电气量辅助选线，可提高选线可靠性。最后，利用仿真验证了故障特征及选线方法的正确性。

不接地系统；高阻接地故障；故障选线；故障特征；适应性分析

在我国，不接地系统在中压配电网当中占据了很大的比例[1-2]。其中，单相接地是最常见的故障类型，其故障（工频）电流一般小于20 A，检测困难[3-7]。特别是由树障、单相断线并坠地、避雷器不完全击穿以及小动物侵入等因素诱发的单相高阻接地故障，故障电流进一步减小、故障点更不稳定，使得故障检测尤为困难[8-9]。由于高阻接地故障（特别是导线断线并坠地）对人身安全的威胁尤为突出，其检测技术也应给予极大的关注。

近年，小电流接地故障选线技术取得了较大进展，代表性方法有暂态法[10-11]、中电阻法[12]、小扰动法[13]、注入信号法[14]等。但现有方法大多针对低阻接地故障，并不能确定是否能适用于高阻接地故障。文献[15]介绍了基于模式识别的高阻接地故障检测方法，这种方法利用小波变换来提取故障特征量，用主成分分析方法完成特征选择，由贝叶斯分类器完成分类。通过使用这种方法，高阻接地故障特征得以从绝缘子泄漏电流ILC（insulator leakage current）和由电容器切换、负载切换（高/低电压）、接地故障、侵入电流和空载线路切换产生的暂态当中区分出来。文献[16]介绍了一种利用残余电压、电流的基频分量来检测不接地系统高阻接地故障的方法，这种方法可以检测到不接地系统发生高阻接地故障时的故障馈线以及故障相，但故障检测灵敏度会受系统不平衡电流和电流互感器比值的影响。

本文根据不接地系统的高阻接地故障等值电路给出了母线零序电压、故障点零序电流、故障线路零序电流和健全线路零序电流等特征电气量的解析表达式。分析了故障暂态电流的峰值与衰减时间及工频电流的峰值随过渡电阻、线路电感、对地电容、故障初始相角的变化规律，进一步对故障线路与健全线路出口故障电流的峰值、极性以及暂态功率方向系数进行了分析比较，从而确定暂态幅值比较、极性比较以及功率方向判别法对于不接地系统高阻接地故障基本适用。可借助故障工频信号来改善现有的选线方法，进一步提高不接地系统高阻接地故障选线的可靠性。最后利用MATLAB仿真对暂态分析、工频分析、适用性分析进行了验证。

1 不接地系统高阻接地故障分析

1.1 不接地系统高阻接地故障等值电路

图1所示为不接地系统高阻接地故障等值电路，对于高阻接地故障暂态电气量和工频电气量均有较高模拟精度。

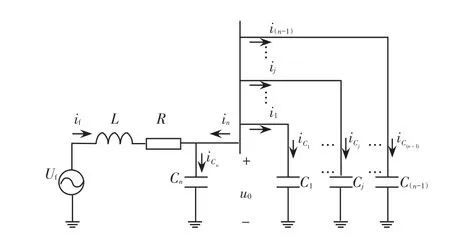
图1 不接地系统高阻接地故障等值电路Fig.1 Equivalent circuit of high-resistance grounding fault in isolated neutral system

设系统共有n条架空线路馈线（其中第n条线路为故障线路）图中，Cj（j=1，2，…，n）为第j条线路对地零序分布电容；iCj为对地零序电容电流；ij为第j条线路出口零序电流；if为故障点零序故障电流；u0为母线零序电压；Uf为故障点处虚拟电源，等于故障点故障前的反相电压；Um为反相电压峰值；ϕ为故障初相角；C为n条馈线对地零序分布电容之和；L为故障点上游的一模电感L1、二模电感L2与零模电感L0之和；R为故障点上游的一模电阻R1、二模电阻R2、零模电阻R0与3倍的接地电阻Rf之和[17-18]。具体计算方法如下：

1.2 故障点电流求解

根据图1，建立线性二阶非齐次微分方程

求解得到其特征根为

根据过渡电阻不同，可分为欠阻尼和过阻尼两种状态下的谐振过程，其中欠阻尼谐振过程可认为是小电流接地系统低阻接地故障时的主谐振过程[17-18]，本文不做更多介绍。

当过渡电阻满足

时，谐振过程为过阻尼状态。对于一般的典型不接地10 kV配电系统，系统对地电容电流一般为1～20 A，对应的系统对地电容C为0.5～10.5 μF；故障点距母线距离一般在0～20 km之间，考虑主变感抗，则对应的故障点上游电感L（包含架空线路电感与主变电感，后面统一称为线路电感）的分布范围为2～114 mH。在上述情况下，临界过渡电阻值分布范围为53～910 Ω。本文以临界过渡电阻值作为高阻接地与低阻接地的分界，重点分析不接地系统的过阻尼谐振过程。

因此，母线零序电压u0的表达式为

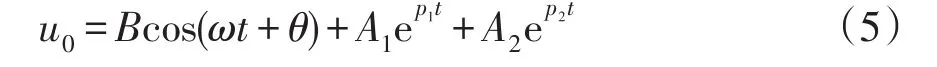
其中：

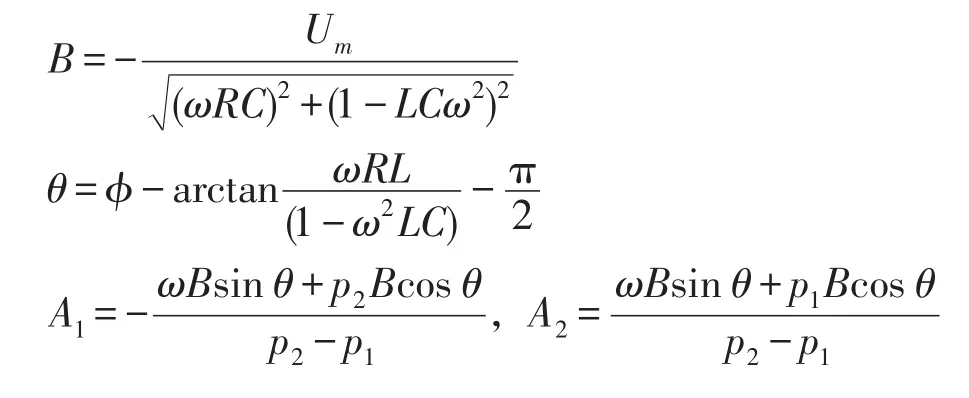
等值电路为RLC串联电路，所以可求得故障点零序故障电流if为

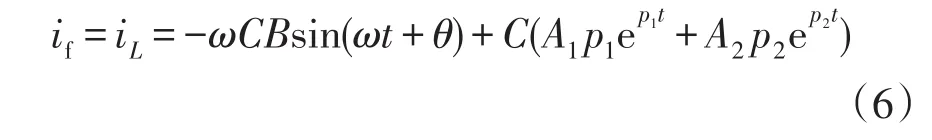
根据得到的表达式可以发现，不接地系统高阻接地故障电流由工频分量与暂态分量组成，其暂态分量为两个衰减直流分量的叠加。

1.3 故障点暂态电流分析

1.3.1 故障暂态电流峰值分析

故障暂态电流ift及其分量ift1、ift2表达式为

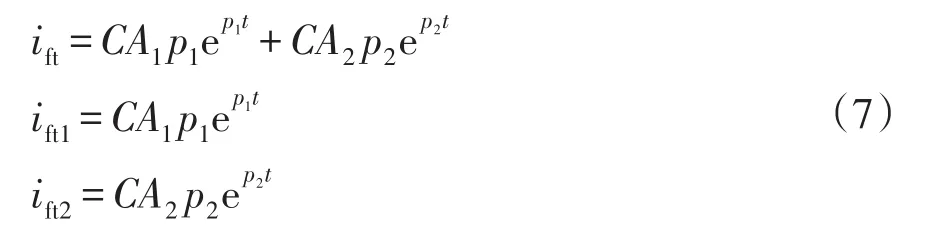
当A1p1、A2p2同号时，故障时刻值就是故障暂态电流峰值。当A1p1、A2p2异号时，若A1A2＜0，故障暂态电流还将存在一个极值。设t0为极值时刻，则故障暂态电流极值iftp表达式为

其中：

故障暂态电流的峰值可能出现在故障时刻，也可能出现在极值时刻，选取这两个时刻较大者作为其峰值。

对于10 kV配电系统，故障点处故障初始相角取90°。设故障点距离母线的距离为10 km不变（对应的线路电感L为60.01 mH），当过渡电阻R在53～3 000 Ω范围内变化，对地电容电流在1～20 A范围内变化时，可以得到故障暂态电流峰值随R与对地电容C的变化关系如图2所示。

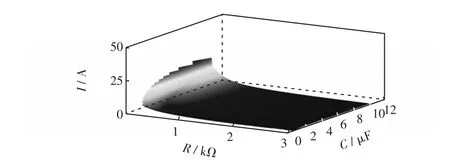
图2 故障暂态电流峰值随过渡电阻及对地电容的变化趋势Fig.2 Tendency of the transient current’s peak value under fault with the change of transition resistance and capacitance to earth

另一方面，设对地电容电流为1.21 A不变（对应的对地电容C为0.67 μF），当过渡电阻R在53～3 000 Ω范围内变化，故障点距离母线的距离在0～20 km范围内变化时，可以得到故障暂态电流峰值随R与L的变化关系如图3所示。

图3 故障暂态电流峰值随过渡电阻及线路电感的变化趋势Fig.3 Tendency of the transient current’s peak value under fault with the change of transition resistance and line inductance

可见故障暂态电流峰值整体上随着R和L的增大而减小，随着C的增大而增大。

从式（8）中可以发现，故障暂态电流峰值还与故障初始相角有关，若故障初始相角从0°等间距增加到360°，记录峰值的最大值与最小值的变化规律，将其与初始相角的关系用散点图的方式表示得到图4。

图4 故障暂态电流峰值最值随初始相角的变化关系Fig.4 Relationship between the maximum of transient current’s peak value under fault and initial phase angle

故障暂态电流峰值随过渡电阻及线路电感的增大而减小，随对地电容的增大而增大，当过渡电阻在53～3 000 Ω内变化、故障点距离母线距离在0～20 km范围内变化、系统对地电容电流在1～20 A范围内变化时，在故障初始相角为90°或270°处可以达到130 A（最大值），在0°或180°处会降到0.03 A（最小值）。

1.3.2 故障暂态电流衰减时间分析

由式（3）可知p1、p2大小与过渡电阻R、线路电感L、系统对地分布电容C有关。p1、p2都一直小于零，前者的模值随R和C的增大而减小，后者的的模值随R、C的增大而增大且总是大于前者的模值，R与C越大，模值之差越大。

由此可得知，故障暂态电流的过渡时间主要与ift1的参数有关，即随着R与C的增大而增大。

另外，经过推导与分析，当RC2＞2L时，过渡时间随线路电感的增大而增大。当RC2＜2L时，过渡时间随线路电感的增大而减小。即在R和C的变化范围一定的前提下，过渡时间的最小值可能会在L变化的下限值或上限值处取到。

仍使用第1.3.1节中的讨论方法与参数，第1项分量为ift1，第2项分量为ift2，得到ift1与ift2的衰减时间与R和C以及与R和L的关系分别如图5和图6所示。

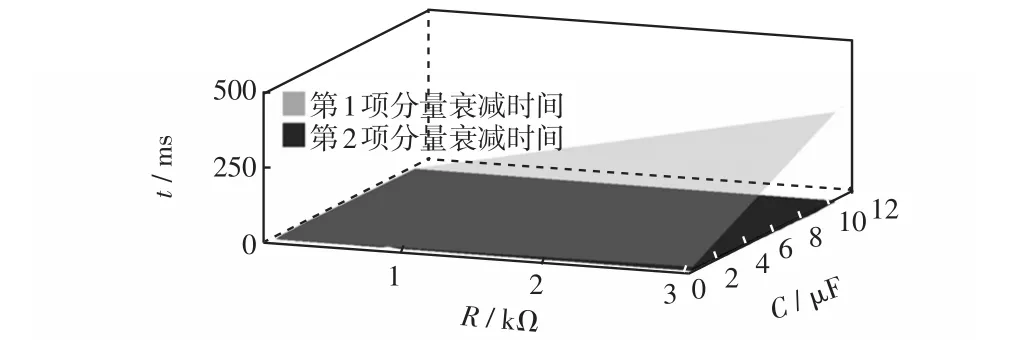
图5 衰减时间随对地电容及过渡电阻的变化趋势Fig.5 Tendency of decay time with the change of capacitance to earth and transition resistance

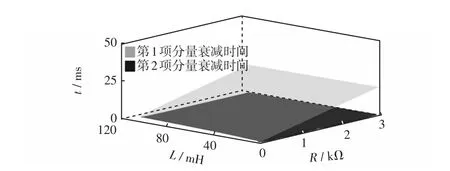
图6 衰减时间随线路电感及过渡电阻的变化趋势Fig.6 Tendency of decay time with the change of line inductance and transition resistance

当过渡电阻在53～3 000 Ω范围内变化、故障点距离母线距离在0～20 km范围内变化、系统对地电容电流在1～20 A范围内变化时，第1项分量的过渡过程的持续时间一直大于0.14 ms，而保护的扫描周期一般为几十微秒，即可以保证在过渡时间内取到采样点，保证故障暂态电流的检测。第2项分量的过渡时间则一直较短，介于1～200 μs之间。

1.4 故障点工频电流峰值分析

故障点处工频电流表达式为

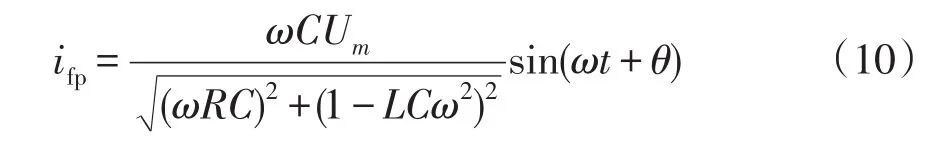
可见其大小与对地电容、线路电感、过渡电阻有关，对式（10）变形后可得到

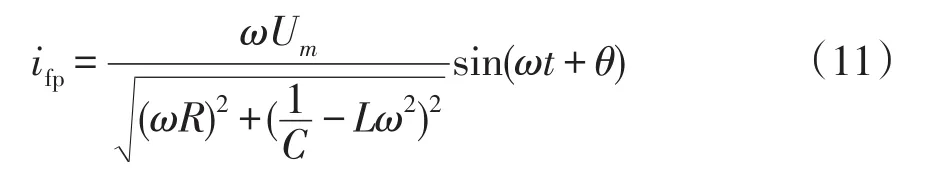
可知，故障工频电流峰值随过渡电阻R的增大而减小，随对地电容C与线路电感L的增大而增大。

使用第1.3.1节中典型参数与讨论方法，其峰值与R和C以及与R和L之间的关系分别如图7和图8所示。

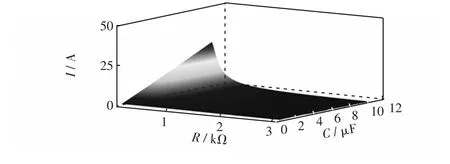
图7 故障工频电流峰值随过渡电阻及对地电容变化趋势Fig.7 Tendency of the power frequency current’s peak value under fault with the change of transition resistance and capacitance to earth

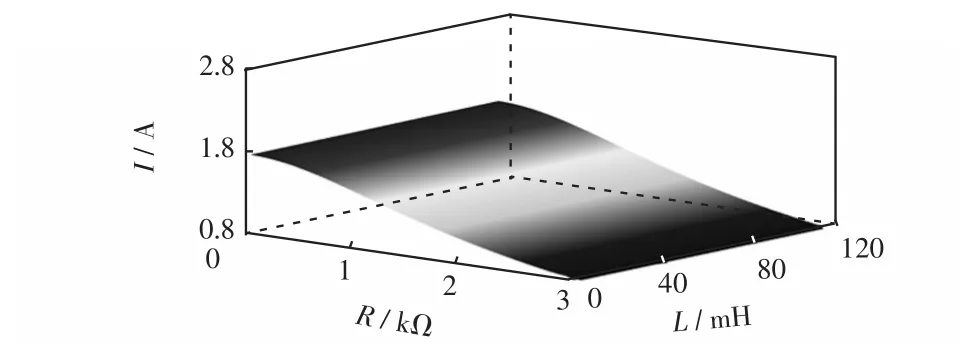
图8 故障工频电流峰值随过渡电阻及线路电感变化趋势Fig.8 Tendency of the power frequency current’s peak value under fault with the change of transition resistance and line inductance

可见L对故障工频电流峰值的影响相对于R、C较小。当R较小，C较大时（取R=53 Ω，C=10.5 μF，对应对地电容电流为20 A），故障工频电流峰值较大（28.10 A）。当R为3 000 Ω，C为0.5 μF（对应对地电容电流为1 A）时，故障工频电流峰值较小（0.8 A）。

综上可知：故障工频电流峰值随过渡电阻的增大而减小，随对地电容与线路电感的增大而增大。在过渡电阻在53～3 000 Ω内变化，系统对地电容电流在1～20 A范围内变化时，工频电流峰值变化范围在0.8～28 A之间。

1.5 故障线路与健全线路故障电流求解与分析

各条馈线自身对地电容电流为

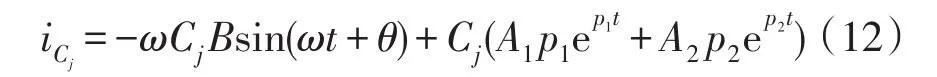
对于n-1条健全线路来说，线路出口电流即为线路自身对地电容电流：ij=iCj,j=1,2,…,n-1。

故障线路出口电流为

可见，各条馈线电流均由工频分量和暂态分量构成，而暂态分量又均为两个衰减直流分量的叠加。

在式（12）和式（13）中，故障线路与健全线路出口的故障暂态电流峰值之比等于工频电流峰值之比，同为（C-Cn）/Cj。所以在不同的故障条件（过渡电阻、线路电感、初始相角、对地电容）下，它们的暂态分量与工频分量之间的大小关系是相同的。在图9中，取对地电容为1.21 A的对地电容电流对应的典型值0.67 μF、线路电感为10 km的故障距离对应的典型值60.01 mH，将故障线路出口的故障电流暂态分量峰值与工频分量峰值同时表示出来，发现前者虽然在多数情况下大于后者，但当故障过渡电阻较大或故障初始相角在0°和180°附近时，会略小于后者。工程要求电流互感器原边电流在1 A以上时才能满足测量要求，本文借助典型配电网参数，通过仿真计算故障线路出口不同故障条件（过渡电阻、故障距离、对地电容条件）下的故障暂态电流与工频电流峰值，发现两者都基本高于1 A，符合测量要求。

图9 故障线路故障电流暂态分量与工频分量峰值随过渡电阻与故障初始相角变化关系Fig.9 Tendencies of the peak values of transient component and power frequency component of fault current with the change of transition resistance and initial phase angle

2 现有选线方法对于不接地系统高阻接地故障适用性

本节分别讨论工频与暂态故障电流及功率对于现有暂态选线方法的适用性，进而可以确定利用其工频分量选线的可靠性以及必要性。

2.1 现有暂态选线方法简介

1）暂态电流峰值比较法

故障发生时，故障线路出口的故障暂态电流峰值最大。选择故障暂态电流峰值最大的线路为故障线路[19-20]。

2）暂态电流极性比较法

故障发生时，故障线路出口的故障暂态电流极性与健全线路的相反。

比较各出线故障暂态电流的极性，如果某条出线和其他所有出线反极性则该出线为故障线路，如果所有出线都同极性则为母线接地[19-20]。

3）暂态综合选线法

如果单纯使用故障暂态电流峰值比较，在母线接地故障时将发生误选。而如果单纯使用故障暂态电流极性比较，在健全线路较短时，信号极易受到干扰而造成误选。可以选择故障暂态电流峰值较大的（至少3条）线路再比较其极性确定故障线路[19-20]。

4）暂态功率方向法

故障线路上暂态零序电压的导数与零序电流始终反极性，而健全线路上电压导数始终与电流极性相同。取T为暂态谐振周期，定义某出线k暂态零序电流ik0（t）和零序电压u0（t）方向系数Dk为

如果Dk＞0，判断为健全线路；如果Dk＜0，判断为故障线路[19-20]。

2.2 故障暂态信号适用性分析

设u0t为母线零序电容暂态电压，第i（i=1，2，…，n-1）条健全线路出口的暂态功率方向系数为

故障线路出口的暂态功率方向系数为

根据式（12）、式（13），故障线路与健全线路出口的故障暂态电流极性一直相反，同时，在常见电力系统模型的参数中C-Cn远大于Cj，所以故障线路出口的故障暂态电流峰值一直明显大于健全线路。

根据图10与仿真验证，当过渡电阻较小时，暂态电流的第1项分量零时刻幅值ift10与第2项分量零时刻幅值ift20都比较大，而当过渡电阻与对地电容都比较大时，ift10的值相对于ift20会比较小。结合图5，即当过渡电阻与对地电容的值较大时，第1项暂态分量的峰值与第2项分量的衰减时间的值都很小，使得暂态电流衰减过快，变得难以测量。

图10 暂态电流两项分量零时刻幅值对比Fig.10 Amplitude comparison between the two components of transient current at zero time point

综上所述，结合故障暂态电流在第1.3节中关于衰减时间的结论与第1.5节中关于峰值条件的结论，上节中所述选线方法对于不接地系统高阻接地故障选线是基本适用的，但在过渡电阻与对地电容较大时选线难度较大。另外，根据第1.5节，当初始相角在0°和180°附近时，故障暂态电流峰值会略小于工频电流峰值。同时故障线路与健全线路出口上的故障暂态电流差值比较小，暂态功率方向系数也较小。

2.3 故障工频信号适用性分析

根据第2.2节，可以进一步得到故障线路出口的工频电流峰值一直明显大于健全线路；另外，由式（12）和式（13）可以得到，故障线路与健全线路出口的工频电流极性一直相反；同时，工频功率方向系数的计算方法和表达形式与暂态功率相同，所以其正负关系相同。

综上所述，结合第1.5节当中的故障电流工频分量的峰值条件，可以用故障工频电流、功率进行辅助选线。根据第1.4节，在过渡电阻较小、对地电容较大时，工频电流峰值较大，有利于工频选线方法的实施，且可靠性高。

在实际应用中，可以测量线路出口的故障暂态电流、工频电流和母线零序电压。若选择电流极性比较法，判断某出线故障暂态电流和工频电流的极性与其他线路不一致的为故障线路，否则为健全线路，若所有出线的故障电流分量的极性都一致则为母线故障；若选择电流幅值比较法，选择线路出口故障暂态电流和工频电流的峰值最大的线路为故障线路；若选择功率方向法，选择暂态与工频功率方向系数为负的线路为故障线路。

当过渡电阻与对地电容较大时，因故障暂态信号测量难度较大，此时应该适当升高采样频率或以工频选线方法为主；当暂态信号较弱（故障初始相角在0°和180°附近）时，亦推荐以工频选线方法为主。否则以暂态选线方法为主。

3 仿真验证

图11为一典型110 kV/10 kV配电网示意，母线出线为5条电缆与架空线混合线路。为使故障暂态现象明显，故障初始相角取90°。在2号线路发生1 500 Ω的高阻接地故障，故障点距离母线10 km。以图11所示的分布参数电路对故障和健全线路出口的故障电流进行仿真讨论。图12给出了故障线路全电流的理论计算值、等值电路仿真波形、系统仿真电路仿真波形的对比结果。

可见理论分析的结果、等值电路仿真波形、系统仿真电路仿真波形三者基本一致，验证了理论分析和等值电路的正确性。

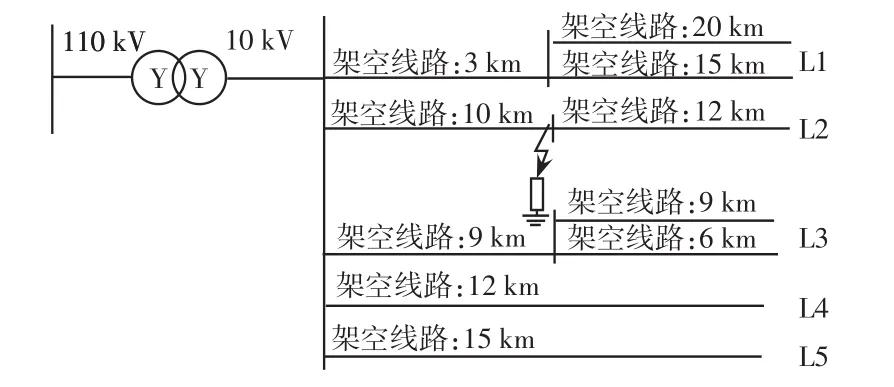
图11 中性点不接地系统仿真模型Fig.11 Simulation model of isolated neutral system at neutral points

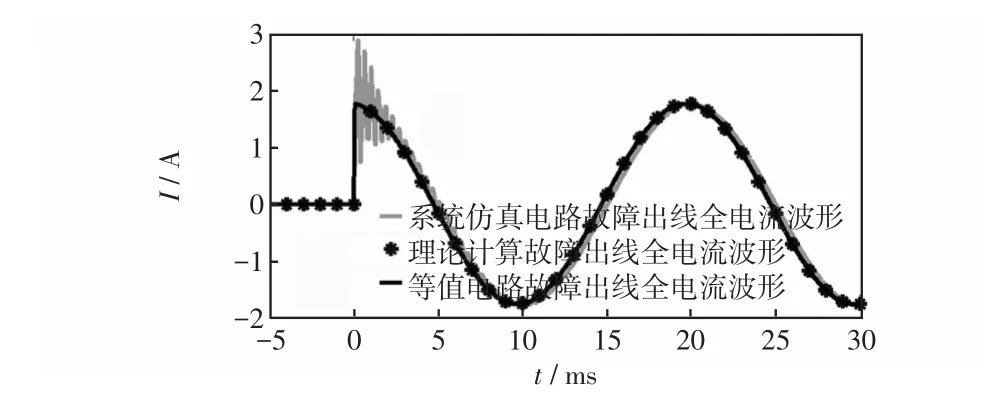
图12 故障线路出口电流的计算值与仿真结果对比Fig.12 Comparison between calculated values and simulation results of fault current

图13给出了故障线路与健全线路故障电流及其分量的时域波形。图13（a）中故障线路的故障暂态电流峰值可达到1 A，而健全线路中其峰值稍高于0.5 A，两者都在大约8 ms后衰减到零，可见故障暂态电流的峰值满足峰值比较法的测量要求。图13（b）中故障工频电流峰值在故障线路中大约为1.8 A，在健全线路中大约为0.3 A，两者的差值可以被识别并被用于故障选线。图13（c）中故障线路与健全线路出口的故障电流极性相反，结合图13（a）、（b）中的峰值与极性条件，可知故障电流及其分量全部满足电流极性比较法的测量条件。

4 结 论

（1）本文通过求解不接地系统单相接地故障的等值电路，分析了故障点电流暂态分量和工频分量的特性。比较了故障线路与健全线路出口暂态电流的峰值、极性，计算了线路出口的暂态功率方向系数，证明了它们的峰值相差足够大、极性相反，符合现有暂态选线方法的测量要求，但在过渡电阻与对地电容较大时因衰减时间太短会增大测量难度，需要提高保护测量的采样频率。

（2）为提高不接地系统高阻接地故障选线的准确性，本文建议使用工频分量进行辅助选线，并从理论上证明其极性与幅值条件仍旧满足幅值比较法、极性比较法和功率方向法的测量要求。

（3）结合故障特征，给出了利用暂态信息与利用工频信息两类选线方法各自的适用条件。

[1]郑顾平，张利，姜超，等（Zheng Guping，Zhang Li，Jiang Chao，et al）.中性点不接地系统单相接地故障区段在线定位（Line and segment one-line location of singlephase-to-earth fault in the ungrounded neutral system）[J].电力系统自动化（Automation of Electric Power Systems），2013，37（3）：110-115.

[2]Grebchenko N V，Maximchuk V F，Pylypenko Y V.The method of determining parameters of single-phase fault in network with isolated neutral[C]//2nd International Conference on Intelligent Energy and Power Systems.Kyiv，Ukraine，2016.

[3]李玲玲，李凤强，王成山（Li Lingling，Li Fengqiang，Wang Chengshan）.基于模糊综合决策的配电网单相接地故障选线（Selecting line based on fuzzy fusion decision-making in single-phase-to-earth of distribution network）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（5）：43-46.

[4]魏子镪（Wei Ziqiang）.小电流接地系统单相弧光接地的选线研究（Research on Line Detection for Single-Phase Arc’s Earthing Fault in Neutral Point Non-Effective Grounded System）[D].天津：天津大学电气与自动化工程学院（Tianjin：School of Electrical Engineering and Automation，Tianjin University），2010.

[5]索南加乐，李宗朋，王莉，等（Suonan Jiale，Li Zongpeng，Wang Li，et al）.基于频域参数识别方法的配电网单相接地故障选线（Fault line selection in distribution networks based on parameter identification method in frequency domain）[J].电力系统自动化（Automation of Electric Power Systems），2012，36（23）：93-97，125.

[6]孔红，郭倩，张巍（Kong Hong，Guo Qian，Zhang Wei）.配电网单相接地故障信号形态学消噪方法（Signal denoising for single-line to ground fault in distribution networks based on mathematical morphology）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（4）：78-82.

[7]赵建文，李科，随晓娜，等（Zhao Jianwen，Li Ke，Sui Xiaona，et al）.多级数据模糊融合选线新方法（New fault line selection method of multilevel fuzzy data fusion）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2016，28（2）：56-60.

[8]李震球，王时胜，吴丽娜（Li Zhenqiu，Wang Shisheng，Wu Lina）.一种谐振接地系统电弧高阻接地故障选线新方法及仿真（A new method and simulation for arcing high-impedance-grounding fault line selection in resonant grounded system）[J].电力系统保护与控制（Power System Protection and Control），2014，42（17）：44-49.

[9]耿建昭，王宾，董新洲，等（Geng Jianzhao，Wang Bin，Dong Xinzhou，et al）.中性点有效接地配电网高阻接地故障特征分析及检测（Analysis and detection of high impedance grounding fault in neutral point effectively grounding distribution network）[J].电力系统自动化（Automation of Electric Power Systems），2013，37（16）：85-91.

[10]薛永端，张秋凤，颜廷纯，等（Xue Yongduan，Zhang Qiufeng，Yan Tingchun，et al）.综合暂态与工频信息的谐振接地系统小电流接地故障选线（Faulty feeder identification based on combined transient and power-frequency components in resonant grounded systems）[J].电力系统自动化（Automation of Electric Power Systems），2014，38（24）：80-85.

[11]刘谋海，王媛媛，曾祥君，等（Liu Mouhai，Wang Yuanyuan，Zeng Xiangjun，et al）.基于暂态相电流特征分析的故障选线新方法（Novel method of fault line selection based on characteristic analysis of transient phase-current）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2017，29（1）：30-36.

[12]周志成，付慧，凌建，等（Zhou Zhicheng，Fu Hui，Ling Jian，et al）.消弧线圈并联中阻选线的单相接地试验及分析（Single phase-to-earth test and analysis for the fault line selection under arc-suppression coil parallel connecting the mid-resistance）[J].高电压技术（High Voltage Engineering），2009，35（5）：1054-1058.

[13]邹浩斌，胡少强，刘利平，等（Zou Haobin，Hu Shaoqiang，Liu Liping，et al）.基于小扰动原理的单相接地选线装置（Single-phase grounding selected-line equipment based on small disturbance theory）[J].继电器（Relay），2007，35（2）：20-24.

[14]王凤，康怡（Wang Feng，Kang Yi）.基于脉冲信号注入法的小电流接地选线技术（Pulse signal injection based faulty line detection for small current neutral grounding system）[J].电网技术（Power System Technology），2008，32（15）：90-93，98.

[15]Sedighi A-R，Haghifam M-R，Malik O P，et al.High impedance fault detection based on wavelet transform and statistical pattern recognition[J].IEEE Trans on Power Delivery，2005，20（4）：2414-2421.

[16]Hou Daqiang，Fischer Normann.Deterministic high-impedance fault detection and phase selection on ungrounded distribution systems[C]//IEEE Industrial and Commercial Power Systems Technical Conference.Edmonton，Canada，2007.

[17]薛永端，李娟，徐丙垠（Xue Yongduan，Li Juan，Xu Bingyin）.中性点不接地系统小电流接地故障暂态等值电路的建立（Construction of transient equivalent circuits of single-phase earth fault for isolated neutral systems）[J].中国电机工程学报（Proceedings of the CSEE），2013，33（34）：223-232.

[18]薛永端，李娟，徐丙垠（Xue Yongduan，Li Juan，Xu Bingyin）.中性点经消弧线圈接地系统小电流接地故障暂态等值电路及暂态分析（Transient equivalent circuit and transient analysis of single-phase earth fault in arc suppression coil grounded system）[J].中国电机工程学报（Proceedings of the CSEE），2015，35（22）：5703-5714.

[19]廖俊宏，帅红，梁伟（Liao Junhong，Shuai Hong，Liang Wei）.小电流接地系统选线方法的灵敏度分析（Sensitivity analysis of fault line detection method in small current grounded system）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2014，26（6）：65-69，80.

[20]郭清滔，吴田（Guo Qingtao，Wu Tian）.小电流接地系统故障选线方法综述（Survey of the methods to select fault line in neutral point in effectively grounded power system）[J].电力系统保护与控制（Power System Protection and Control），2010，38（2）：146-152.

Characteristics of High-resistance Grounding Fault in Isolated Neutral Systems and the Adaptability Analysis of Fault Line Selection

PAN Benren1，GUAN Tinglong2，GUI Xiaozhi1，XUE Yongduan2，GUO Liang1
（1.Electric Power Research Institute，State Grid Jiangxi Electric Power Company，Nanchang 330096，China；2.College of Information and Control Engineering，China University of Petroleum（East China），Qingdao 266580，China）

In an isolated neutral system，compared with the low-resistance grounding fault，the high-resistance grounding fault current is smaller and the fault location is more unstable，which leads to higher difficulty in fault line selection.Based on a fault equivalent circuit，the high-resistance grounding fault characteristics of power frequency current and transient current in the isolated neutral system are analyzed，and the power frequency and transient current information are compared between the fault and healthy lines.The changing rule of the fault current under different fault conditions（e.g.，fault resistance，line inductance，capacitance to earth and initial phase angle）is obtained.It is proved that the line selection methods such as transient current amplitude comparison，polarity comparison and transient power direction selection can also be applied to the isolated neutral system under high-resistance grounding fault.Moreover，if the fault power frequency information is applied to assist the line selection，then the selection reliability will be improved.Finally，simulation results verify the validity of fault characteristics and line selection methods.

isolated neutral system；high-resistance grounding fault；fault line selection；fault characteristis；adaptability analysis

TM74

A

1003-8930（2017）10-0052-08

10.3969/j.issn.1003-8930.2017.10.010

2017-04-25；

2017-06-30

国家自然科学基金资助项目（51477184）；国家电网公司科技资助项目（521820150008）

薛永端（1970—），男，博士，教授，研究方向为配网自动化、配电网接地方式与接地故障自愈技术。Email:xueyb70@126.com

潘本仁（1983—），男，硕士，高级工程师，研究方向为继电保护及配电自动化技术研究。Email：pbr168@163.com

管廷龙（1995—），男，硕士研究生，研究方向为小电流接地系统高阻接地故障检测。Email：guantinglong-1020@163.com

桂小智（1987—），男，硕士，研究方向为继电保护电能质量。 Email：gxz61612@163.com