城市自助式公共出租车的网点布局

杨新湦，王 倩，彭 巍，高志波

(1. 中国民航大学 空中交通管理学院，天津 300300；2. 长沙理工大学 交通运输工程学院，湖南 长沙 410075)

城市自助式公共出租车的网点布局

杨新湦1，王 倩1，彭 巍2，高志波2

(1. 中国民航大学 空中交通管理学院，天津 300300；2. 长沙理工大学 交通运输工程学院，湖南 长沙 410075)

基于“汽车共享”的理念，提出了一种适合城市内部短时双向出行的交通方式——自助式公共出租车。通过自助式公共出租车乘车意向调查和需求分析，在灰色预测法预测出的总规模限制下，先基于供需平衡得到备选网点布局方案，再综合考虑社会总投资和各用户利益，建立双层规划模型，用模拟退火算法得到网点布局优化方案。最后，以长沙市为例进行实例分析，将运算方案与其他方法计算出的方案进行了比较。研究结果表明：模拟退火算法是一个有效的算法，双层规划模型可以很好的应用到网点布局优化。经济效益分析得出网点布局方案符合社会需求、满足经济效益。

交通工程；双层规划模型；模拟退火算法；网点布局；自助式公共出租车

自助式公共出租车是基于“汽车共享”理念的一种新的出租车运营服务。汽车共享起源于1948年的瑞士，目前全球有30多个国家、600多个城市开展了汽车共享。主要有3种形式：邻里汽车共享、车站汽车共享和多节点汽车共享模式，前两种都必须完成双程路途，而后者属于单程路途[1]。国内，汽车共享属于新兴行业，个别城市开展或试运了类似汽车共享的汽车租赁服务，但汽车租赁与出租车是分开的，自助式公共出租车还没在相关城市推行。

国内外学者对“汽车共享”问题的研究大多以宏观角度从理论上分析该模式的现状、前景及社会效益，基于理论分析及实际操作的研究非常少。A．KARBASSI等[2]提出了一种汽车共享中路线预测和到达时间评估方法；A．G．H．KEK等[3]针对汽车共享多车场间车辆调配问题，创新性建立了3阶段最优模拟决策系统，设计混合整数线型规划模型，用启发式算法求解出结果；S．A．SHAHEEN等[4]分析了引入汽车共享后对城市交通系统的影响，从而得出汽车共享项目具有环保、节约社会效应的结论；且丽莎[5]建立了需求完全满足与需求不完全满足的确定性空车调配模型；邱雷[6]对上海消费者对于汽车共享服务接受程度的市场调研，提出了汽车共享服务在中国市场的前景和营销策略；李仕鹏[6]以汽车共享过程中所有顾客总损失时间为目标，针对车辆配置问题建立了汽车共享排队模型；周彪等[8]从出行者选择行为出发，应用离散选择模型，得出汽车共享对城市居民的主要吸引因素；程苑[9]基于演化博弈论思想，建立引入汽车共享的城市公共交通出行方式的博弈模型，分析汽车共享与私家的影响过程。

综上所述，目前大多数研究以定性和理论研究为主，而在实际操作中的定量分析研究仍很少，在服务规模、网点布局、车辆调配、动态定价等方面较少涉及。因此，亟需从定量分析的角度来完善自助式公共出租车的相关规划研究。

1 问题描述

随着经济社会发展，我国已进入机动化时代，快速增长的私家车使得交通拥堵、能源短缺、环境污染、安全事故等问题日趋严重。在降低小汽车所带来的负外部性影响方面存在两种思路：一是限制小汽车发展，比如限购，但实施阻力很大；二是提高小汽车使用效率，目前国外的成功做法是汽车共享，在提高小汽车使用效率上有显著成效。我国一些城市也尝试过拼车、出租汽车合乘等，但由于相关法律法规不健全，个人利益、隐私与人身安全得不到保障，这些尝试都不太成功。

笔者针对城市交通状况，根据“汽车共享”理念，提出了一种安全环保的新型公共交通出行方式——自助式公共出租车。根据乘车的意向调查分析，最终确定服务人群为有个性化需求和驾驶许可证但经济条件受限的年轻人群，计价方式采取时距并计的方式，车型为两座电动车。从社会和用户角度而言都具有很大意义，不仅填补了城市短时出租的空白，在保留私家车便捷性的同时又能有效提高汽车使用效率。

自助式公共出租车网点布局的目标是寻找使交通网络的社会效益最大的投资决策方案，即研究如何能用最少的资金投入达到使用户盈余最大的目的。针对离散型的交通网点的规划，常用的模型有整数规划模型、运输模型、CFLP法、双层规划模型等，而这些模型都可用禁忌搜索法、模拟退火法、遗传算法等启发式算法求解。遗传算法早熟并难以处理非线性约束，禁忌搜索法则依赖于初解，无法保证全局最优，模拟退火算法运算时间长[10]。

2 网点布局

自助式公共出租车的需求受人口密度及出行者选择意愿的影响，其中人口密度又受附近公共场所、住宅区的影响，出行意愿选择受交通运输和经济发展水平的影响[11]。综上所述，将自助式公共出租车网点布局的影响因素归纳如表1。

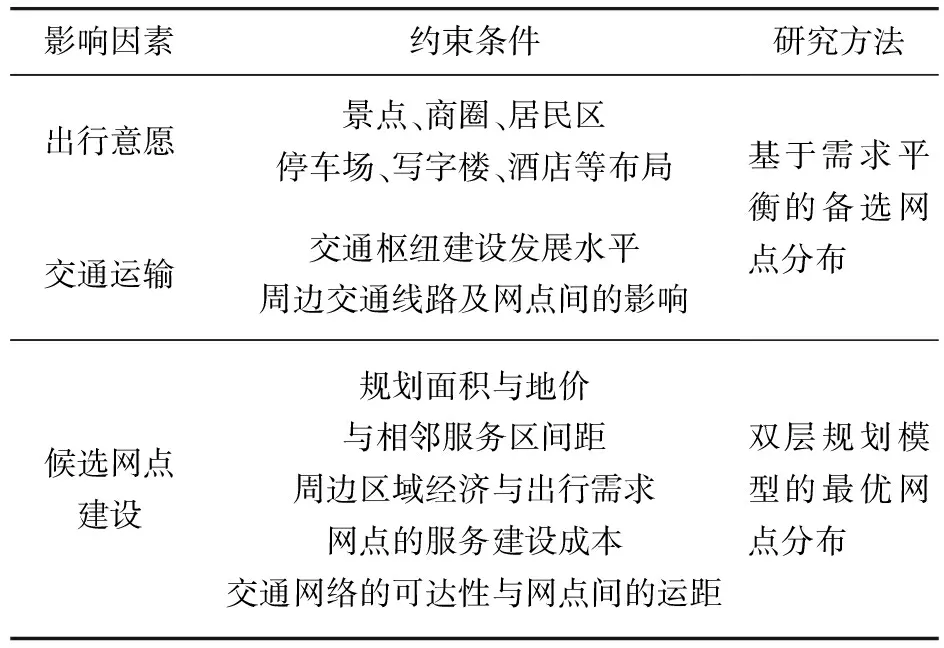
表1 网点布局研究思路Table 1 Network layout research idea

2.1 基于供需平衡二维网点选址模型

基于供需平衡二维网点选址采用的是定性与定量分析结合方法，由二维定性分析得到基于供需平衡的备选网点布局方案；目标是以最小的网点数量满足区域内的租赁需求水平，也就是要求在区域内任意一点的服务水平不小于需求水平时，网点总规模N最小的情况，如式(1)[12]：

(1)

式中：Ln为N个网点的位置矩阵；矩阵Ln中网点n所在的位置数值为1；Sij为i到j所提供的服务；qij为i到j的需求。

根据研究区域的需求矩阵设定标准网点的服务能力在中心位置为30，按照服务水平从中心开始衰减，构造服务模式矩阵A如式(2)：

(2)

租赁网点的服务矩阵S是N个网点服务情况的和，其表达如式(3)：

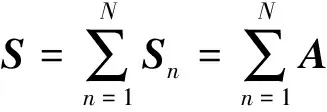
(3)

式中：⊗代表二维离散卷积分运算。

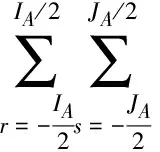
(4)

式中：Sn(i,j)为从网点n到点(i,j)所提供的服务；Sn为包含Sn(i,j)离散值的供应矩阵(I×J)；IA和JA分别代表网点服务模式矩阵A的行数和列数。

2.2 双层规划模型的网点布局优化

2.2.1 建模思路

自助式公共出租车的网点布局问题需要从社会总投资和用户使用成本来综合考虑，但用户与系统的利益往往是相互冲突的，属于双目标优化问题。笔者建立双层规划模型，上层规划模型目标是使得社会总投资最小，给下层提供网点布局方案。下层规划模型用户为保证出行的广义费用最低，进行出行线路选择，进行反馈调整，最终得到满足系统整体费用最优，又能最大限度的满足顾客的利益需求的布局方案[13]。

2.2.2 模型建立

1)决策空间

为更好的描述旅客出行的交通选择过程，绘制出相应的出行网络图，如图1。

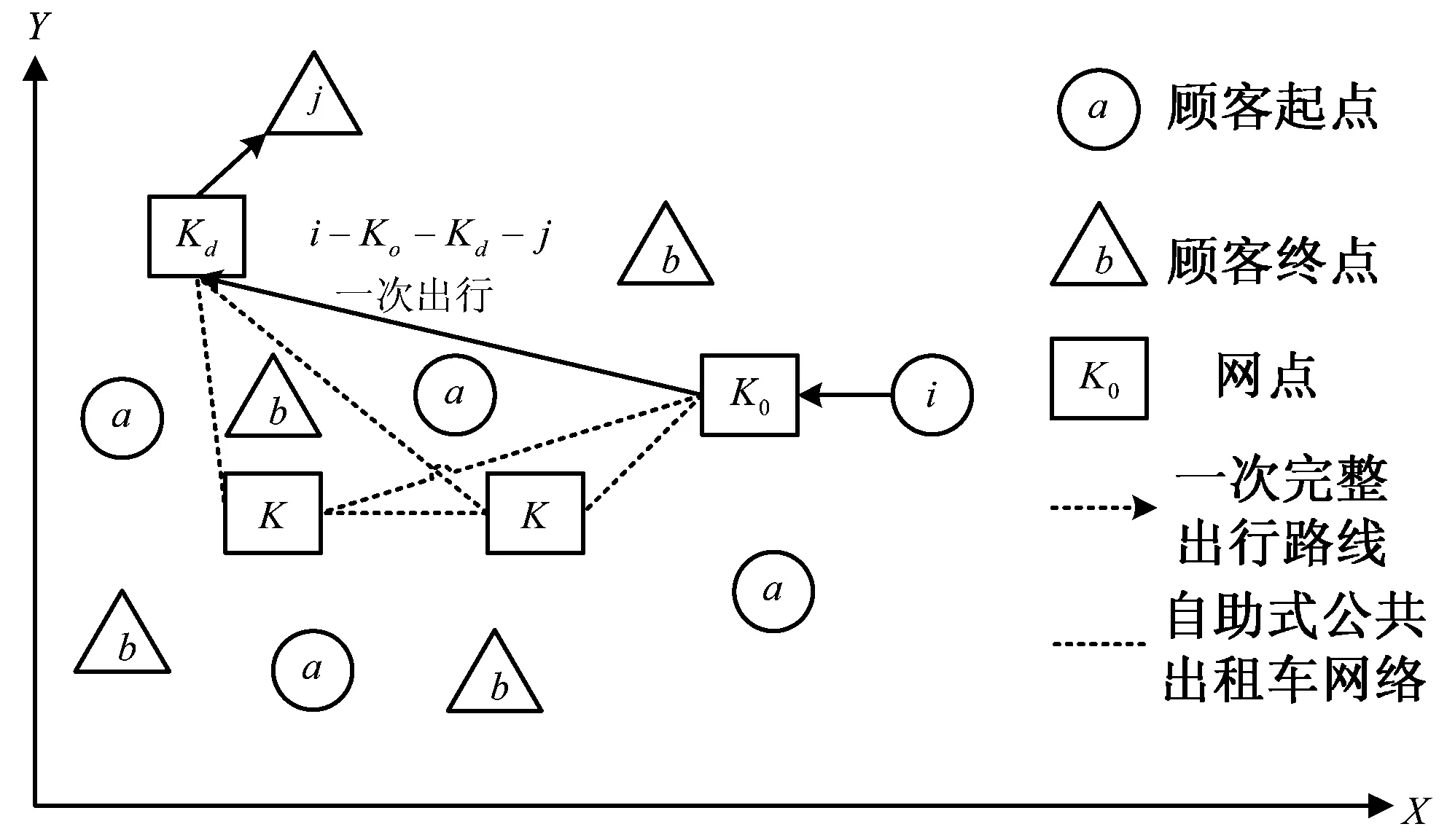
图1 交通网络Fig.1 Traffic network

定义一次完整的出行(i-ki-kj-j)以i点出发，步行至出发地附近的网点ki乘自助式公共出租车到目的地附近的网点kj，再步行到目的地j点。

定义自助式公共出租车网络结构有：A={i|i=1,2,…,m}为交通需求点集；B={j|j=1,2,…,m}为交通吸引点集；E={k|k=1,2,…,n}为自助式公共出租车网点集。

2)决策变量

规模变量为zk，其中：k=(1,2,…,n)。

3)目标函数

上层规划模型：社会效益(社会总投资费用最小)。

社会总投资包括出行费用和固定投资费用，自助式公共出租车出行费用采取时距并计的方式，笔者考虑到车辆周转，给出低速限制vmin，当v≤vmin时，在按距离计费的基础上，计算低速行驶的费用。固定投资费用包括网点的建设费用以及车辆费用。

(xkykαk+gkykcksk)

(5)

泊位数与规模的对应关系：

gk=(1+β)zk

(6)

最小规模约束：

zk≥nf

(7)

总规模约束：

(8)

覆盖范围约束：

(9)

式中：N、nf分别为总规模和最小规模；qij、dij、wij、tij、xij分别表示i点到j点的流量、距离、车辆周转率、时间和车辆数；θ为单位低速行驶时间费用，取θ=24元/h；αk为车辆价格，αk=2×105元/辆；Sk为每车占地面积，Sk=2.5×5m2/辆；Ck为单位面积地价；Rk为网点k的服务半径，km；gk为网点k的泊位数；vmin=12 km/h；β为规模与泊位数的平衡系数；λ为负指数分布常数。

下层规划模型：用户利益——各用户的广义费用最低。

广义费用考虑用户完成一次完整出行的时间成本和出行成本，建立函数：

(10)

网点k的规模zk为需求点i(j)到离该需求点附近的网点k的车辆数xiki(xjkj)之和：

(11)

由流量与车辆数对应关系xij=qij/μwij，可得以下的需求约束：

(12)

非负约束：

zk-Myk≤0

(13)

式中：tikikjj、xikikjj分别为一次完整的出行的时间和车辆数；ai为i点的需求总量；bj为j点的吸引总量；Cw为单位距离的步行费率；Cz为自助式出租车单位距离费率；M表示无限大；μ为平均载客率，μ=1.5人/车。

3 模拟退火算法

自助式公共出租车双层规划模型的求解属于NP难问题，采用模拟退火，针对算法运算时间长的缺点，基于供需平衡得到初始的布局方案，再利用模拟退火算法求解网点布局的双层规划模型，通过降温过程的不断递归运算最终确定一组最优解。

退火过程由一组初始参数，即冷却进度表控制，其核心是尽量使系统达到准平衡，以使算法在有限的时间内逼近最优解[14]。算法流程如图2，冷却进度表包括：

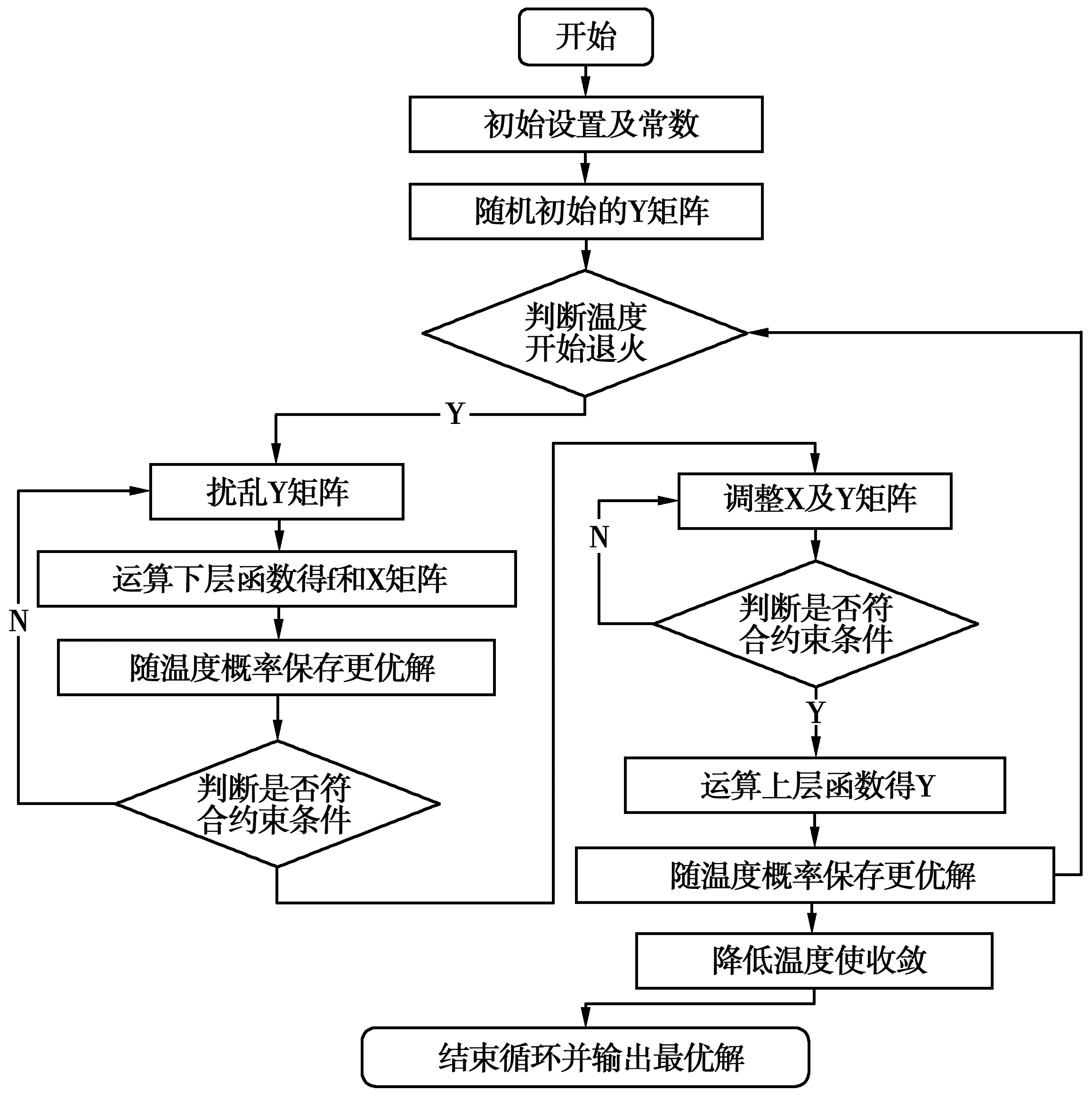
图2 算法的流程Fig.2 Algorithm flow chart

1)控制参数的初值T0：冷却开始的温度，可设置T0=97；

2)控制参数T的衰减函数：因计算机只能处理离散数据，因此需要把连续降温过程离散化成降温过程中的一系列温度点，衰减函数即计算这一系列温度的表达式，这里采用的衰减函数为：

Tk+1=αTk，k=0, 1, 2, …,L

式中：α为参数，这里α取值为0.9。

3)控制参数T的终值Tf(停止准则)，可设置Tf=3；

4)Markov链的长度Lk：任一温度T的迭代次数。从经验上说，对简单的情况可以令Lk=100n，n为问题规模，可取Lk=10 000。

4 实例分析

笔者将长沙市西起麓谷公园、东至湖南农业大学；北起开福区政府、南至长沙汽车南站的(18×18)km2的范围作为研究区域。对该区域进行二维离散化处理，划分为(1×1)km2小区域，以点代格。进行评价指标的量化，根据定性和定量分析，得到研究区域的需求矩阵。再根据数值处理及MATLAB运算，求解基于供需平衡的选址模型得到自助式公共出租车网点布局的位置矩阵L，并绘制相应的备选27个网点分布，如图3。

由图3可直观的看出部分网点分布不合理，存在网点相邻现象；布点数较多，与给定的规模不相符；考虑因素不全面，如网点建设成本、网点间的运费、网络效益没考虑到。因此，笔者在备选网点的基础上建立双层规划模型进行优化选址。

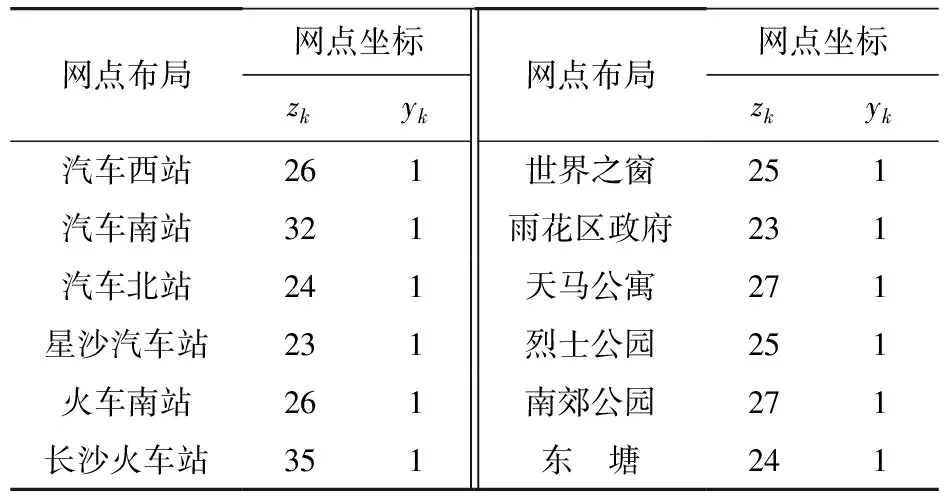
MATLAB编程计算得出网点坐标如表2。将求解结果在地图上标出，如图4。

MATLAB求解得出双层规划模型的最优网点布局方案，从方案图表中能直观看出各网点的规模。在优化网点布局中可知：网点的服务范围广，布局合理，进一步验证了模型及算法的可行性。

为更好地进行方案对比，把简单需求模型的布局方案进行求解并进行绘图(图5)，并与文中模型做了简单对比分析，如表3。

自助式公共出租车是一种很有前景的出行方式，具有很大的经济与社会效益。由计算得出，如果根据满足调查得到的居民需求来计算，则自助式公共出租车在长沙市可以替代91 387辆私家车，节省了16.8万t汽油、减少了305 232 t CO2的排放量，能够为长沙市城市交通减少75 399个公共停车位，同时可以减少7 400 km的汽车行驶里程。分析证明：自助式公共出租车具有较好的社会与经济效益。

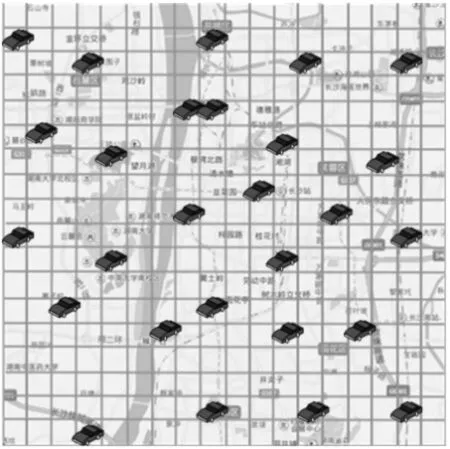
图3 备选网点分布Fig.3 Alternative scheme of network layout

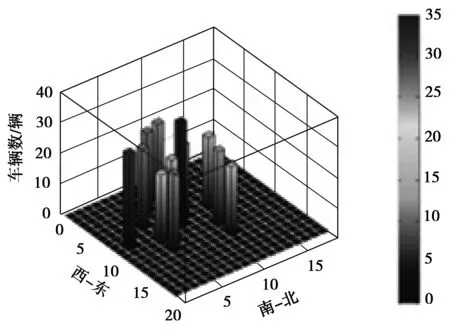
图4 优化网点布局Fig.4 Optimization scheme of network layout

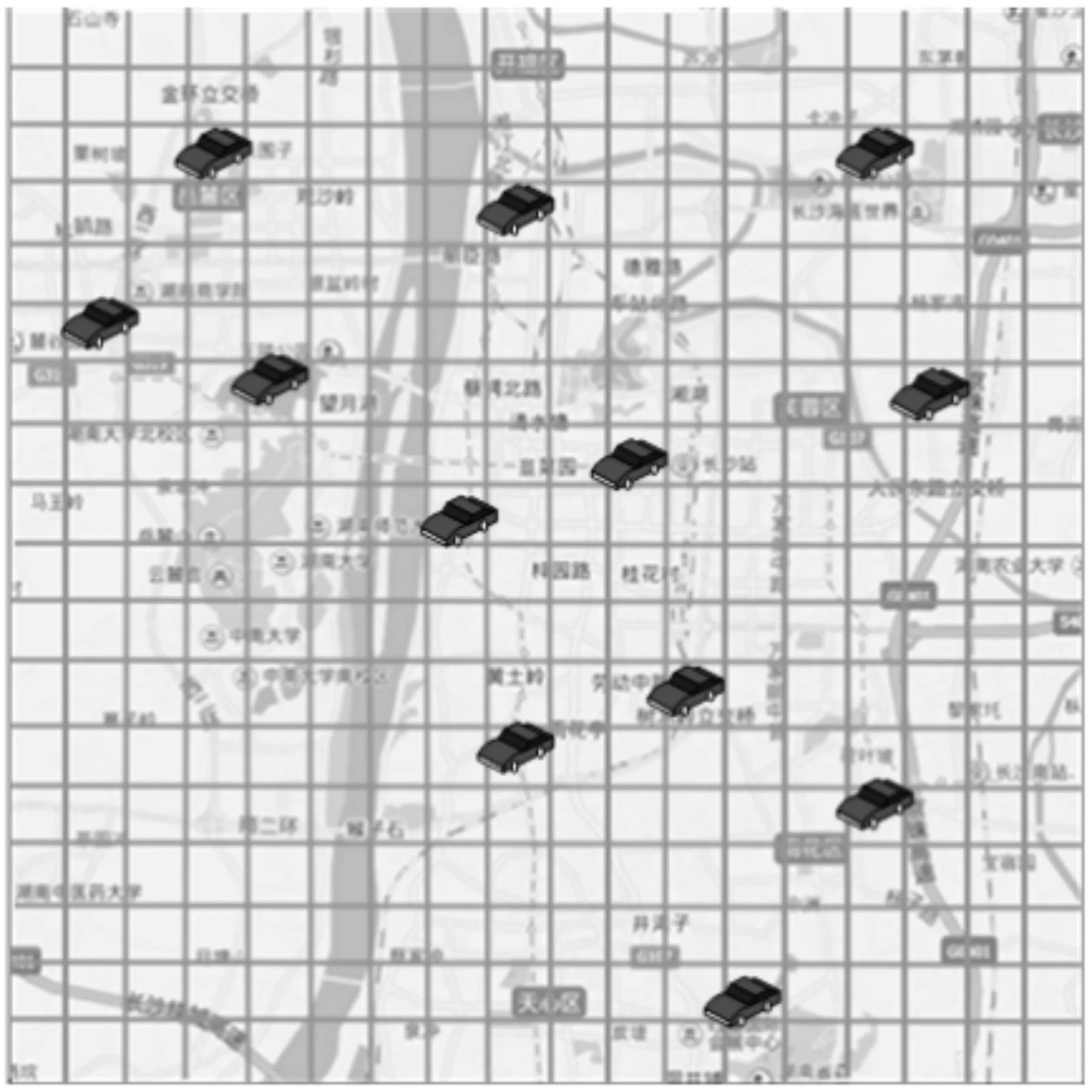
图5 基于距离的网点分布Fig.5 Distance-based network layout

网点布局网点坐标zkyk网点布局网点坐标zkyk汽车西站261世界之窗251汽车南站321雨花区政府231汽车北站241天马公寓271星沙汽车站231烈士公园251火车南站261南郊公园271长沙火车站351东 塘241

表3 网点布局方案分析Table 3 Analysis on network layout scheme

5 结 论

1)新型的交通供给方式。通过分析国内外先进的交通理论，笔者针对城市的交通症结提出一种更有前景的公共交通出行方式——自助式公共出租车，使汽车共享与传统出租车行业相结合，找到一种适合城市内部短时双向出行的交通方式。

2)更优化的网点布局模型。由于现有网点布局规划实践过程中，数据不精确，考虑不全面，收敛效果不好，使得模型算法选择的风险较大，存在不确定性。因此，笔者把定量分析与定性分析相结合，得到基于供需平衡的二维网点布局的初始网点布局方案，再建立双层目标规划模型用模拟退火算法得到最优方案。

3)对长沙市自助式公共出租车的经验进行总结，逐步拓宽服务领域，向整个中南地区推广，继而向全国和部分国外地区推广，让自助式公共出租车的可持续发张、低碳环保的用车理念深入到人心。

自助式公共出租车具有较好的社会与经济效益，可以向国内外推广。自助式公共出租车可用于大中城市新建城区、公交盲点区域及小汽车限行的区域。模型算法适用于常见规划当中，可进一步向国内推广，让可持续发展、低碳环保的用车理念深入人心。在笔者已开发的软件基础上，可进一步开发软件的附加功能，对成果进一步的转化。

[1] 周溪召．国外汽车共享的发展状况分析[J]．中国科技投资，2013(A10)：19-20．

ZHOU Xizhao. Analysis of the development status of foreign car sharing [J].ChinaVentureCapital, 2013(A10): 19-20.

[2] KARBASSI A, BARTH M. Vehicle route prediction and time of arrival estimation techniques for improved transportation system management [J].IEEEIntelligentVehiclesSymposium, 2003, 93(1): 511- 516.

[3] KEK A G H, CHEU R L, MENG Qiang, et al. A decision support system for vehicle relocation operations in car-sharing systems [J].Trans-portationResearchPartE:LogisticsandTransportationReview, 2009, 45(1): 149-158.

[4] SHAHEEN S A, CANO L A, CAMEL M L. Electric vehicle car-sharing in a senior adult community in San Francisco bay area [C]//TransportationResearchBoard92ndAnnualMeeting. Washington D.C.: TRB, 2013.

[5] 且丽莎．基于“汽车共享”的空车调配问题研究[D]．成都：西南交通大学，2010．

QIE Lisha.StudyofEmptyCarAllocationBasedonthe“Car-sharing”[D]. Chengdu: Southwest Jiaotong University, 2010.

[6] 邱雷．汽车共享服务在中国的市场前景与营销策略研究[D]．上海：复旦大学，2009．

QIU Lei.StudyontheMarketProspectandMarketingStrategyofCarSharingServiceinChina[D].Shanghai: Fudan University, 2009.

[7] 李仕鹏．基于排队论的汽车共享优化设计[D]．杭州：杭州电子科技大学，2013．

LI Shipeng.AnOptimizationDesignApproachofCar-sharingBasedonQueuingTheory[D].Hangzhou:Hangzhou Dianzi University, 2013.

[8] 周彪，周溪召，李彬．基于上海市消费者的汽车共享选择分析[J]．上海理工大学学报，2014，36(1)：97-102．

ZHOU Biao, ZHOU Xizhao, LI Bin.ChoiceanalysisofcarsharinginconsiderationoftheconsumersinShanghai[J]. Journal of University of Shanghai for Science and Technology, 2014, 36(1):97-102.

[9] 程苑．汽车共享下的城市交通出行方式博弈研究[D]．哈尔滨：哈尔滨工业大学，2015．

CHENG Yuan.ResearchonaGameProcessofUrbanTransportModeunderCar-Sharing[D].Harbin:Harbin Institute of Technology,2015.

[10] 宋阳．汽车租赁网点规划布局理论与方法[D]．北京：北京交通大学，2012．

SONG Yang.TheoryandMethodofCarRentalNetworkandLocationPlanning[D].Beijing:Beijing Jiaotong University,2012.

[11] 李明，刘航，张晓建．多物流配送中心的选址布局问题优化模型研究[J]．重庆交通大学学报(自然科学版)，2017，36(1)：97-102．

LI Ming, LIU Hang, ZHANG Xiaojian. Research on the optimization model of site selection and layout of logistics distribution center [J].JournalofChongqingJiaotongUniversity(NaturalScience), 2017, 36(1): 97-102.

[12] 徐艳会．ATM机服务网点的区域布局与优化问题研究[D]．石家庄：河北师范大学，2010．

XU Yanhui.ResearchonATMMachineServiceNetworkoftheReginalDistributionandOptimization[D].Shijiazhuang: Hebei Normal University, 2010.

[13] 李利华．不确定性物流网络设计的区间规划模型与算法研究[D]．长沙：中南大学，2012．

LI Lihua.ModelsandAlgorithmsofIntervalPlanningforUncertainLogisticsNetworkDesign[D].Changsha: Central South University, 2012.

[14] 孟杰，陈庆樟，张凯．基于模拟退火算法的汽车悬架最优控制研究[J]．重庆交通大学学报(自然科学版)，2013，32(3)：497-501．

MENG Jie, CHEN Qingzhang, ZHANG Kai. Optimal control of vehicle suspension based on the simulated annealing algorithm [J].JournalofChongqingJiaotongUniversity(NaturalScience), 2013, 32(3): 497-501.

NetworkLayoutofUrbanSelf-servicePublicTaxi

YANG Xinsheng1, WANG Qian1, PENG Wei2, GAO Zhibo2

(1.College of Air Traffic Management, Civil Aviation University of China, Tianjin 300300, P.R.China; 2.School of Traffic and Transportation Engineering, Changsha University of Science and Technology, Changsha 410075, Hunan,P.R.China)

According to the theory of “car sharing”, self-service public taxi is a means of transportation which is suitable for the short-time bi-directional travel in the city. The investigation on the intention of self-service public taxi and demand analysis was carried out. Under the limit of the total scale which was solved by grey forecast method, the alternative scheme of network layout based on the balance between supply and demand was obtained; on this basis, considering the total social investment and users’ interests, the bi-level programming model was established and the optimal scheme of network layout was obtained by the application of simulated annealing algorithm. At last, the empirical analysis was carried out in Changsha; the calculation scheme was compared with the schemes calculated out by other methods. The research results show that the simulated annealing algorithm is an effective algorithm, and bi-level programming model can be a good application to the network layout optimization. The economic benefit analysis shows that the network layout scheme meets the needs of the community and economic benefits.

traffic engineering; bi-level programming model; simulated annealing algorithm; network layout; self-service public taxi

10.3969/j.issn.1674-0696.2017.11.17

2016-05-11；

2016-10-24

杨新湦(1966—)，男，陕西扶风人，教授，主要从事空中交通管理计机场枢纽策略方面的研究。E-mail: xsyang@cauc.edu.cn。

王 倩(1992—)，女，湖南湘阴人，硕士研究生，主要从事空中交通规划与管理方面的研究。E-mail: 809521927@qq.com。

U491.1+23；U113

A

1674-0696(2017)11-090-06

(责任编辑：刘韬)