大跨径连续钢桁梁桥悬臂拼装线形控制方法研究

王 玲，王 韬，王荣霞

(河北工业大学 土木与交通学院，天津 300401)

大跨径连续钢桁梁桥悬臂拼装线形控制方法研究

王 玲，王 韬，王荣霞

(河北工业大学 土木与交通学院，天津 300401)

以某在建大跨径连续钢桁梁桥施工过程为背景，对半悬臂拼装过程的线形控制方法进行研究。采用有限元软件Midas Civil建立了钢桁梁主桥的施工阶段模型，通过分析不同预抬高对拼装过程控制线形的影响，推导出预抬高的合理设置公式，确定了钢梁架设的起始安装位置及悬拼过程的控制线形，并结合施工监控数据进行分析。结果表明：实测线形与预测线形基本吻合，说明设置预抬高的线形控制方法实用有效。

桥梁工程；悬臂施工；钢桁梁；临时墩；失稳；控制线形

0 引 言

大跨径桥梁施工过程复杂，由于安装线形与施工过程密切相关，不同的施工过程及施工措施会得出不同的安装线形[1]。近年来，桥梁建设的跨径越来越大，施工过程的线形控制问题逐渐成为施工过程分析的重点研究内容。李传夫等[2]针对大跨径钢管混凝土拱桥吊装的过程的线形控制问题，提出一种迭代优化算法，预先确定拱桥的合理施工状态，计算出了各吊点的预抬高和扣索索力，提高了施工过程中钢管拱肋轴线竖向误差的控制精度。张建民等[3]采用一阶分析法，对千米级斜拉桥施工过程中斜拉索的初始张拉力进行分析，确定了悬臂拼装过程的合理施工状态，并且将一阶最优化分析法引入了斜拉桥的施工控制系统。对于半悬臂法中对拼装线形起重要作用的临时墩结构，胡广周等[4]结合榕江特大桥的设计与施工情况，较系统的推导了临时支墩标高的合理计算公式。

采用临时墩支墩半悬臂施工的大跨径钢桁梁桥，在悬臂拼装过程中，悬臂段的长度逐渐变大，由于钢结构轻质、柔度大的结构特点，前端下挠过大，容易出现偏离设计线形的问题，如不采取措施，将造成无法顺利拼装至前方临时墩或桥墩的问题。

笔者研究拼装过程控制线形的一种控制措施，即通过设置施工预抬高的方式，减少挠度带来的影响，以使施工过程的线形得到有效控制，同时对施工过程进行优化。

1 工程概况

在建的某黄河公路大桥主桥全长876 m，采用下承式变截面连续钢桁梁结构，分跨布置为102+168×4+102 m，主桁采用不带竖杆的华伦式桁架布置，主桁中心距为27 m，主墩处桁高23 m，共用墩及跨中桁高10 m，标准节间长度为14 m，纵向共58个节段。钢桁梁由上弦杆、下弦杆、腹杆、纵横梁、上平联、桥门架组成。上、下弦杆、腹杆、纵横梁采用Q370qE钢材；上平联、桥门架杆件采用Q345qE钢材。结构布置见图1。

图1 大桥结构(单位：cm)Fig. 1 Structure of the long span bridge

该桥首跨采用临时支墩就位安装法，自第2跨开始，采用悬臂拼装法拼装钢梁。首跨81#-80#墩节间拼装完毕后，主墩处节点标高调整至设计标高。钢梁架设中间跨80#-77#墩用100 t履带吊在12 m栈桥上悬臂拼装，边跨77#-75#墩间用100 t履带吊在岸上悬臂拼装。

2 拼装控制线形分析

某在建黄河公路大桥钢桁梁主桥80#～75#梁段采用单向悬臂法拼装，最大悬臂长度达到了105 m，而拼装过程中钢桁梁结构呈现悬臂长、柔度大等结构特点，因此，为了对线形进行有效控制，将先架设梁段节点预抬高，来减小挠度过大带来的不利影响。为了确定合理的控制线形，采用倒退分析法对预抬高的设置进行分析。

2.1 倒退分析法

倒退分析法的基本思想是：在成桥结构理想初始状态下，按实际施工步骤的逆过程，对结构进行倒拆，分析每次拆除一个施工段的结构构件对剩余结构的影响，直至所有构件全部拆完[5-7]。倒退分析各个阶段得到的结构位移和内力状态便是结构施工到该阶段的理想状态，按照这些状态将所有构件全部正装回去，最后得到的就是理想成桥状态[8-9]。

2.2 施工过程仿真分析

以有限元软件Midas Civil建立了钢桁梁主桥施工阶段计算模型，见图2。由于该桥钢梁与桥墩之间设置支座，建模时以边界约束代替支座及临时墩支点，主要分析上部结构施工阶段的线形变化；荷载主要考虑自重及施工荷载。该阶段钢梁自79#桥墩向78#桥墩拼装，悬拼至临时墩L9后，临时墩抄垫，继续向78#桥墩进行拼装，见图3。

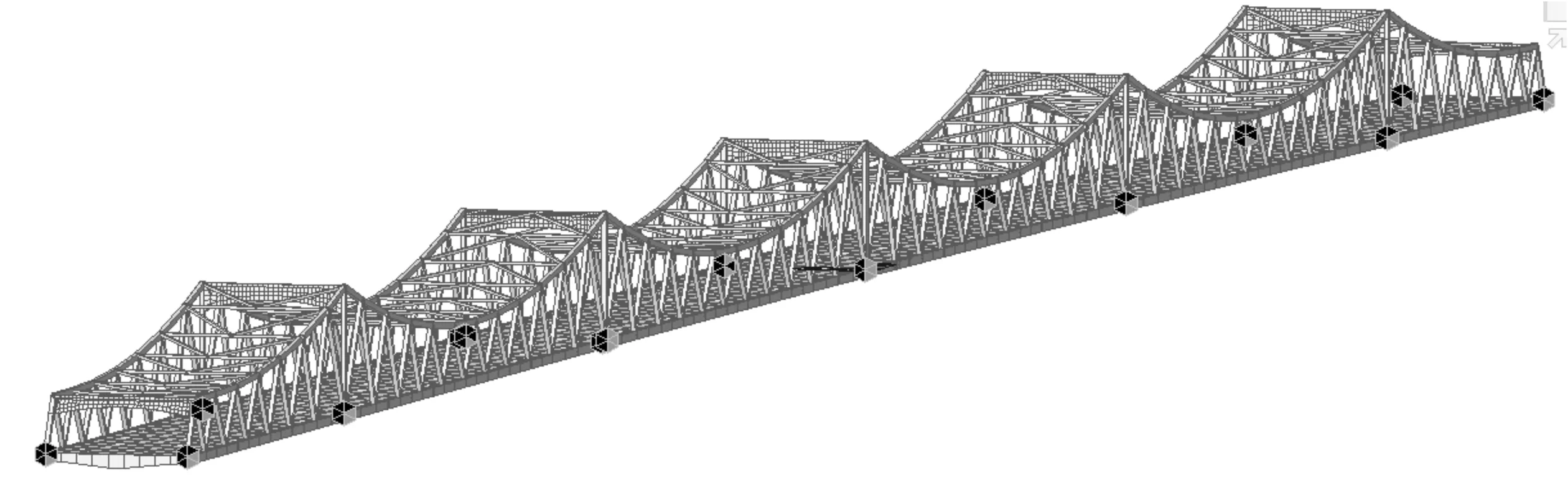
图2 钢桁梁桥有限元模型Fig. 2 The finite element model of steel truss girder bridge

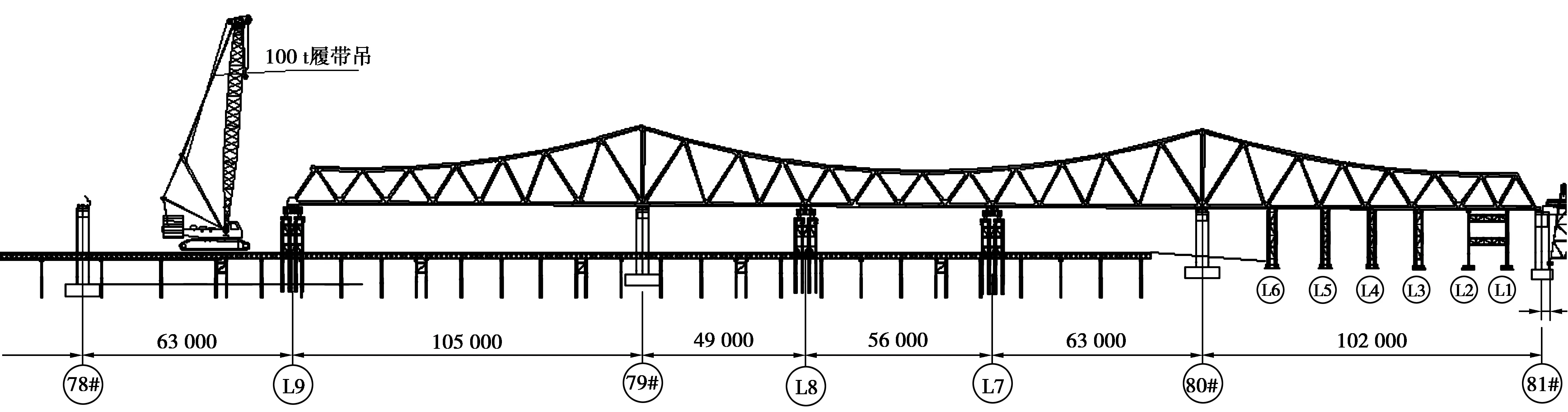
图3 大桥施工示意Fig. 3 Construction schematic of long span bridge

以下弦杆轴线作为钢梁线形研究对象，对悬臂长度最长的79#-78#梁段进行分析，下弦杆节点编号见图4，计算结果见表1。

图4 钢桁梁桥79#-78#节段下弦杆节点编号Fig. 4 Numbering of lower chord node at 79#-78# section of steel truss girder bridge

Table1Frontenddeflectionunderthelargestcantilevercondition

施工阶段架设状态钢梁节点悬臂长度/m前端下挠量/mm工况1到达L9X26105-421．2工况2到达78#X3063-281．1

通过对施工过程进行分析可以看出，该阶段的线形控制目标即使得钢梁悬臂端的标高到达前方支点标高，此时支点反力为0，然后将钢梁垫紧以完成体系转换。这一阶段存在两个最大悬臂状态。由表1知，悬拼到临时墩L9为第1个最大悬臂状态，前端下挠为421.2 mm；悬拼至78#桥墩为第2个大悬臂状态，前端挠度达到281.1 mm。

2.3 不同预抬高对悬臂施工的影响

针对钢桁梁结构柔度大的特点[10]，考虑采用在支点设置预抬高的方式来达到线形控制的目的。由于采用的是部分抬高的方法，挠度的变化量与抬高量并不相同。为分析预抬高对控制线形的敏感性，以表1悬臂端下挠量为依据，取不同预抬高值，最大悬臂工况下弦杆轴线的线形变化见图5。由图5可知，支点抬高后，最大悬臂状态的线形有明显的变化，悬臂端标高的变化幅度大于支点抬高的变化幅度。由此可见，合理确定抬高值对悬臂施工合拢至前方桥墩有着重要影响。

图5 下弦杆轴线的线形Fig. 5 Linear of the lower chord axis

2.4 预抬高的设置公式推导

为进一步研究预抬高的合理取值，将预抬高与挠度变化量的关系进行拟合，得出的结果见图6。由图6可知，钢梁悬拼体系转换前，预抬高与前端的挠度呈线性关系。

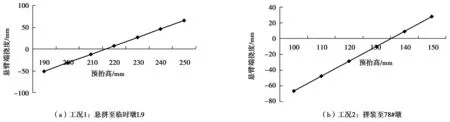
图6 挠度变化Fig. 6 Deflection change

采用线性函数来拟合两者的关系，可以得出体系转换前的预抬高设置公式：

h=αw+β

(1)

式中：h为该阶段预抬高；w为悬拼过程梁端最大挠度；α、β为线性方程系数,由计算结果进行参数拟合得到。

79#-78#梁段的钢梁拼装经历了一次体系转换，将预抬高设置在79#墩顶进行一次预抬时，需要分别计算体系转换前、体系转换后两个阶段的预抬高，并且考虑体系转换后对体系转换前的影响。应用式(1)得

h1=α1w1+β1

(2)

h2=α2w2+β2

(3)

式中：h1为体系转换前预抬高；h2为体系转换后预抬高；w1为体系转换前的最大挠度；w2为体系转换后的最大挠度；α1、α2、β1、β2为线性方程系数, 由模型理论计算结果得到。

考虑体系转换后对体系转换前的影响，推导一次预抬高的合理设置公式为

H=α1(h2+w1)+β1

(4)

式中：H为一次预抬高。

式(4)为所拼装梁段内存在一次体系转换、两个悬拼阶段的一次预抬高设置公式，当所拼装的梁段内设有两个临时墩时，拼装过程有3个悬臂状态，相应的一次预抬高公式为

H=α1[α2(α3w3+β3+w2)+β2+w1]+β1

(5)

式中：H为多次体系转换的预抬高公式；αi、βi为线性方程系数, 由模型理论计算结果得到，i=1，2，3。

根据以上推导过程可知，式(5)能够适用于采用同类施工方法的钢桁梁桥，使用时可以根据临时墩位置进行多次迭代计算。

2.5 控制线形及钢梁起始安装位置

依据式(4)可知，在悬拼段起始位置设置预抬高后，钢桁梁的拼装控制线形与不设置预抬高的控制线形对比见图7，表2。由图7可见，设置预抬高后，不需要在前方支点进行标高调整即可使得钢梁顺利到达前方支墩，减少施工过程中千斤顶的加卸载过程，从而降低了钢梁拼装过程线形控制的难度。由表2可知，考虑抬高，可以减少千斤顶在临时墩墩顶的顶程，避免千斤顶过大的反力对临时墩稳定的影响，线形控制较易，施工过程合理简便，并由此得出了79#钢梁的起始安装位置及临时墩的定位标高。

线形控制79#墩起始安装标高/m临时墩L9定位标高/m千斤顶起顶位置千斤顶起顶量/mm千斤顶起顶反力/t设置预抬高52．85153．23178#墩顶300．00(临时墩不起顶)不考虑预抬高52．55152．529临时墩L9墩顶702．2660．7

3 钢桁梁拼装过程线形监测分析

该在建大桥采用了设置预抬高的方法对施工过程的线形进行控制。在施工过程中，在每一个节间上下游两端选取下弦杆底缘作为标高观测点进行现场监测，最后将实测结果与理论计算结果进行对比,结果见表3。

表3最大悬臂工况高程监测

Table3Heightmonitoringunderthelargestcantileverconditionm

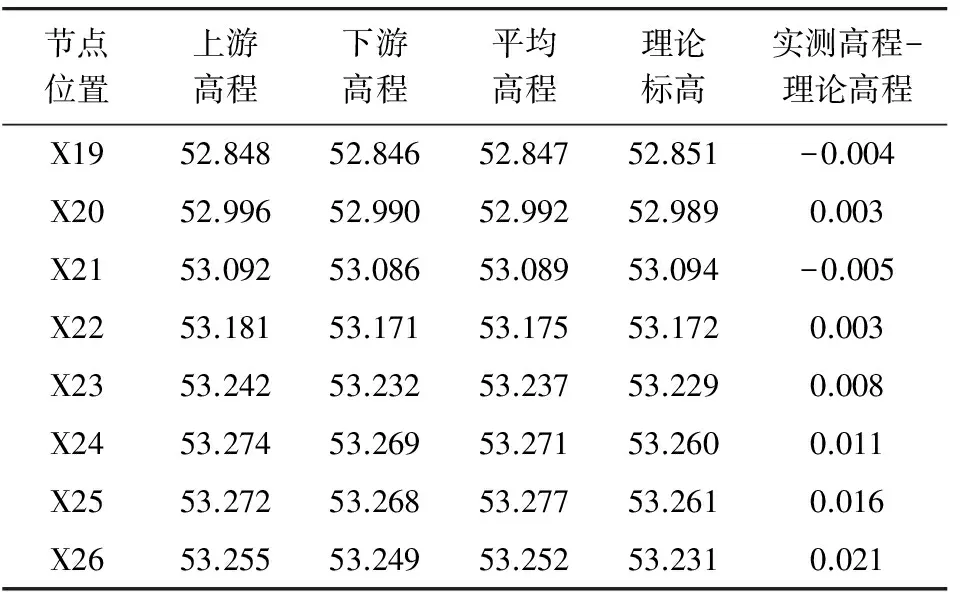
节点位置上游高程下游高程平均高程理论标高实测高程-理论高程X1952．84852．84652．84752．851-0．004X2052．99652．99052．99252．9890．003X2153．09253．08653．08953．094-0．005X2253．18153．17153．17553．1720．003X2353．24253．23253．23753．2290．008X2453．27453．26953．27153．2600．011X2553．27253．26853．27753．2610．016X2653．25553．24953．25253．2310．021

由表3可知，悬拼段的实测高程总体趋势与理论高程一致；实测高程略高于理论高程，高程误差由悬拼根部逐渐累积至悬拼前端，最大误差为2.1 cm。由此可见，采用设置预抬高的钢梁实际线形良好，优化了在前方支墩的调整工作，使得钢梁悬拼线形可控，减少了施工中的不确定性，降低了施工难度。

对于实际监测分析所产生的误差，可以采用千斤顶进行小幅度微调，以保证拼装过程的精度要求。

4 结 论

某在建黄河大桥主跨为168 m，是国内唯一一座大跨径连续钢桁梁桥，分跨多、跨径大、结构复杂，由此带来了一系列施工中的技术难题。通过对大桥的施工过程进行分析，得出以下结论：

1)对于采用悬臂拼装的大跨径多跨连续钢桁梁桥，随着悬臂长度的增加，悬臂端的挠度也随之变大。如悬臂端挠度控制不当，将造成钢梁拼装困难、千斤顶顶程加大、临时墩失稳等一系列问题。因此，应重视施工过程中的线形控制问题。

2)以往的工程案例中，对于预抬高设置的研究并不多见，然而对于该连续钢桁梁桥而言，悬臂长度大，结构柔度大，预抬高对线形的控制起到了关键作用。通过建立有限元模型，分析了预抬高对拼装线形的敏感性，并以倒退分析的思路推导了半悬臂拼装多临时墩施工法一次预抬高的设置公式，该公式对于采用悬臂施工法的长联大跨钢桁梁桥具有普遍适用性。

3)通过对施工过程中千斤顶反力、起顶量的对比，分析了悬臂拼装过程的控制线形，计算出了钢梁的起始安装位置。

4)建设中的黄河公路大桥钢桁梁主桥采用了设置预抬高的方法对拼装线形进行控制，通过对线形监测结果的分析，验证了这一控制方法的合理性与实用性，这为我国大跨径钢桁梁桥施工积累了经验。

[1] 余昆,李景成.基于无应力状态法的悬臂拼装斜拉桥的线形控制[J].桥梁建设,2012,42(3):44-49.

YU Kun, LI Jingcheng. Geometric shape control of cantilever assembled cable-stayed bridge based on unstressed state method [J].BridgeConstruction, 2012, 42 (3): 44-49.

[2] 李传夫, 李术才,魏建军,等.迭代优化算法在大跨拱桥线形控制中的应用[J].山东大学学报(工学版), 2008, 38(3):23-27.

LI Chuanfu, LI Shucai, WEI Jianjun, et al. Application of the iterative optimum method in alignment control of long-span arch bridge[J].JournalofShandongUniversity(EngineeringScience), 2008, 38 (3): 23-27.

[3] 张建民,肖汝诚.千米级斜拉桥施工过程中的索力优化与线形控制研究[J].土木工程学报, 2005, 38(7):54-60.

ZHANG Jianmin, XIAO Rucheng. Cable force optimization and linetype control for the construction of a thousand-meter scale cable-stayed bridge[J].JournalofCivilEngineering, 2005, 38 (7): 54-60.

[4] 胡广周,谭庆波.大跨度连续钢桁架拱桥半悬臂拼装临时墩合理标高计算[J].广东土木与建筑, 2013(3):9-11.

HU Guangzhou, TAN Qingbo. Calculation of the reasonable elevation of the temporary piers of the cantilever erection of the large span continuous steel truss arch bridge[J].GuangdongCivilEngineeringandArchitecture, 2013 (3): 9-11.

[5] 向中富.桥梁工程控制[M].北京:人民交通出版社,2011.

XIANG Zhongfu.ConstructionControlofBridge[M].Beijing: China Communications Press, 2011.

[6] 徐君兰.大跨度桥梁施工控制[M].人民交通出版社,2009.

XU Junlan.ConstructionControlofLong-spanBridge[M].Beijing: China Communications Press, 2009.

[7] 位东升,蔡雄庭.粉房湾长江大桥钢桁梁架设方案比选及线形控制[J]. 桥梁建设, 2012, 42(增刊1):54-59.

WEI Dongsheng, CAI Xiongting. Erection scheme comparison and geometric shape control of steel truss girder of Fenfangwan Changjiang River Bridge[J].BridgeConstruction, 2012, 42(Sup1): 54-59.

[8] 王俊,向中富.特大跨钢桁拱桥建造技术[M].北京:人民交通出版社, 2014.

WANG Jun, XIANG Zhongfu.ConstructionTechnologyofLargeSpanSteelTrussArchBridge[M].Beijing: China Communications Press, 2014.

[9] 项海帆.高等桥梁结构理论[M].北京:人民交通出版社,2013.

XIANG Haifan.AdvancedTheoryofBridgeStructures[M].Beijing: China Communications Press, 2013.

[10] 刘智芳. 台风区大跨度钢桁架拱桥施工控制关键技术研究[D]. 广州：华南理工大学, 2014.

LIU Zhifang.StudyonCrucialTechniqueofConstructionControlforLong-spanSteelTrussArchBridgesinTyphoonArea[D].Guangzhou: South China University of Technology, 2014.

LinearControlMethodofCantileverAssemblyofLongSpanContinuousSteelTrussBridge

WANG Ling, WANG Tao, WANG Rongxia

(School of Civil and Transportation Engineering, Hebei University of Technology, Tianjin 300401, P.R.China)

Taking the construction process of a large span continuous steel truss bridge as the background, the linear control method of the cantilever assembly process was studied. The finite element software MIDAS Civil was used to establish the steel truss beam bridge model in construction phase. Through the analysis on the effect of different pre-elevation on the linear control of assembly process, the formula for pre-elevation reasonable setting was derived, which determined the initial installation position of steel girder erection and the control alignment of the suspension process. Combined with the construction monitoring data, the analysis was carried out. The results show that the measured alignment is basically consistent with the predicted alignment, which indicates that the linear control method of setting pre-elevation is practical and effective.

bridge engineering; cantilever construction; steel truss girder; temporary pier; instability; control line shape

10.3969/j.issn.1674-0696.2017.11.03

2016-08-04；

2017-02-13

王 玲(1976—)，女，河北邯郸人，副教授，博士，主要从事结构工程方面的研究。E-mail：wlarkl@sina.com。

U443.3

A

1674-0696(2017)11-011-05

(责任编辑：谭绪凯)