三峡库区应急资源鲁棒优化配置研究

杨家其，张文芬,2

(1武汉理工大学 交通学院，湖北 武汉 430063;2.武汉理工大学 智能交通系统研究中心，湖北 武汉 430063)

三峡库区应急资源鲁棒优化配置研究

杨家其1，张文芬1,2

(1武汉理工大学 交通学院，湖北 武汉 430063;2.武汉理工大学 智能交通系统研究中心，湖北 武汉 430063)

按照海事管辖范围划分三峡库区水域，并以国家相关规定为依据，综合考虑水域风险，分析三峡库区各水域应急资源的不确定需求. 在探讨水上救助基地应急资源配置机理的基础上，以应急资源配置总损失和总时间最小为目标，构建三峡库区水上救助基地应急资源鲁棒优化配置模型. 以巡逻船为例，得到各种不确定需求情形下的巡逻船配置优化方案. 研究结论表明：鲁棒优化配置方案基本能实现总配置效果优化。当扰动需求总数位于中间值时，三峡库区水上救助基地巡逻船配置系统表现出较好的稳定性，此时巡逻船的机动性较强，巡逻船配置总量最低。研究成果有助于决策者的风险偏好选择，实际应用意义较强，也可为内河相似水域应急资源配置提供决策参考。

交通运输工程；三峡库区；不确定需求；鲁棒优化；应急资源配置

0 引 言

三峡库区位于山区河流，河道弯曲，水上险情多发，在三峡库区实施水上应急救援时，应急资源是人命财产救助的关键应急力量，也是海事管理部门实施水上安全监管和环境保护的主要保障资源，《国家水上交通安全监管和救助系统布局规划》初步规划了三峡库区水上应急救援救助综合基地位置，但应急资源配备数量暂无明确规定。

国内外专家和学者在资源配置优化方面取得了重要研究进展。在资源配置优化目标方面：许建国[1]将资源配置周期划分为多个时间段，以最大化需求覆盖率和需求满足程度为目标，构建了应急服务设施的选址和配置模型；A·ZARDECKI等[2]归纳了动态规划的初始和最终问题，构建了最小化预计时间和最大化预计可能性的目标函数；F.FIEDRICH等[3]分析了地震后应急资源在不同救援地点的失效情形，分析影响死亡人数的因素，建立了SAR期内最小化死亡人数的优化配置模型；GWO·H·TZENG等[4]在考虑应急资源转运的情形，以最小化总费用、总运输时间，最大化需求点的最低满足率为目标函数，建立了救援系统的分配模型。在多阶段的资源配置方面：LI Xiang等[5]将应急时期划分为多个阶段，在满足最基本的需求和道路容量的约束下，构建了多阶段的应急资源分配模型；高学英[6]综合考虑应急点配置的和未配置的应急资源应急效用和配置成本，构建了多阶段的应急资源配置组合优化模型；D·VLACHOS等[7]考虑经济和环境因素，以及制造业供应链的诸多影响因素，制定了长期的动态需求计划。在不确定资源配置领域：张玲[8]考虑供应点应急资源的总投入和调度费用，建立了不确定需求的应急资源配置的两阶段模型，利用鲁棒优化方法进行求解；J·SALMERON等[9]考虑事故地点和严重程度不确定性，建立了两阶段的资金优化配置模型，以实现最少的人员伤亡；J·B·SHEU[10]认为时变需求跟受伤人员密切相关，构建了应急物流管理模型；B·SUN等[11]采用模糊粗糙集理论对应急资源需求进行评价；P·M·CAIN[12]以品牌市场占有率的时间序列为基础数据，建立了动态需求分析的系统方法；左静等[13]通过以往案例统计条件概率，构建了基于贝叶斯和云模型的铁路应急救援模型。

现有研究多按照需求制定应急资源配置计划，且针对内河应急资源优化配置的研究成果十分匮乏，由于我国水上应急救援存在明显的属地管理特征，且应急管理资金严重不足，传统理论配置方案在实际应用中受到很大的限制。为规避由于属地管理导致的资源权属问题，本研究结合国家相关文件规定和要求，按照海事管辖责任范围，将三峡库区水域进行划分，以国家内河巡逻船配置的相关规定为依据，综合考虑水域风险，分析三峡库区巡逻船的不确定需求，以此来制定巡逻船的配置计划，实际应用性更强。

1 三峡库区水域应急资源需求分析

1.1 水域划分及概况

依据《国家水上交通安全监管和救助系统布局规划》，在三峡库区水域范围内将建成重庆、万州、三峡3个水上救助综合基地，按照海事管辖责任范围，本研究将三峡库区共划分为12个水域，如三峡水域指的是三峡海事局所管辖的水域范围，各水域范围(长江上游航道里程)和跨江大桥数量如表1，其中三峡水域含有三峡大坝五级船闸和葛洲坝，为简化研究可视为含有8座跨江大桥。

表1三峡库区水域概况

Table1ThegeneralsituationofThreeGorgesReservoirarea

水域序号水域名称水域范围/km航道里程/km跨江大桥数量/座1巴南719～6902932朝天门690～61179113长寿611～5684324涪陵568～44911975忠县449～3836626万州383～3067737云阳306～2416518奉节241～1905119巫山190～14446110巴东144～10440111归州104～6339012三峡63～3．5608

(资料来源：长江海事局网站，长江电子航道图)

1.2 应急资源配置依据

近年来，我国制定了若干水上应急救援文件，对部分应急资源种类和数量有明确要求。现以巡逻船为例，分析应急资源配置的要求。三峡库区水上应急救援巡逻船主要包括40 m级，30 m级和20 m级3种类型。《海事船舶配备管理规定》中指出内河水域40 m级巡逻船基本配置数量为240 km配置1艘，30 m级巡逻船配置规定如式(1)，20 m级巡逻船的配置规定与30 m级巡逻船类似。

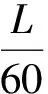
(1)

式中：d30m为30 m级巡逻船配置数量；L为水域航道里程；α为水域风险值；n为跨江大桥数量；β为需求调整系数，受跨江大桥的安全技术性能和所处水文交通环境的影响，取值在1～2之间。

三峡库区航道总里程为715.5 km，依据此规定，共需配置3艘40 m级巡逻船，重庆、万州、三峡3个水上救助基地各一艘，无需进一步研究。因此，笔者以30 m级巡逻船为例探讨三峡库区巡逻船的配置，20 m级巡逻船的配置思路可参考30 m级巡逻船。

1.3 水域风险值的测算

水域风险值能反映出水域风险状况，不同水域风险值不同。水上事故次数是衡量水域风险程度的重要指标，本部分综合考虑三峡库区各水域事故等级和数量，确定出各水域风险值，水域风险值的计算公式如式(2)。其中事故总数为各等级事故数之和，笔者采用1～4“四级标度法”统一事故量纲，以小事故为基准，将一般事故、较大事故、重大事故进行转化，并计算加权之和求得。

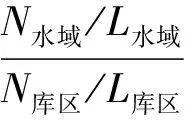
(2)

式中：α为水域风险值；N水域表示库区某水域水上事故总数；L水域表示库区某水域航道里程；N库区表示库区水上事故总数；L库区表示库区航道里程。

据长江海事局2008—2012年水上交通事故统计资料，并结合表1和式(2)可得到三峡库区各水域水上事故等级频次、事故总数和的水域风险值如表2。

表2三峡库区水域水上事故概况和风险值

Table2SurveyandriskvalueofwateraccidentsinThreeGorgesReservoirarea

1.4 三峡库区水域应急资源需求分析

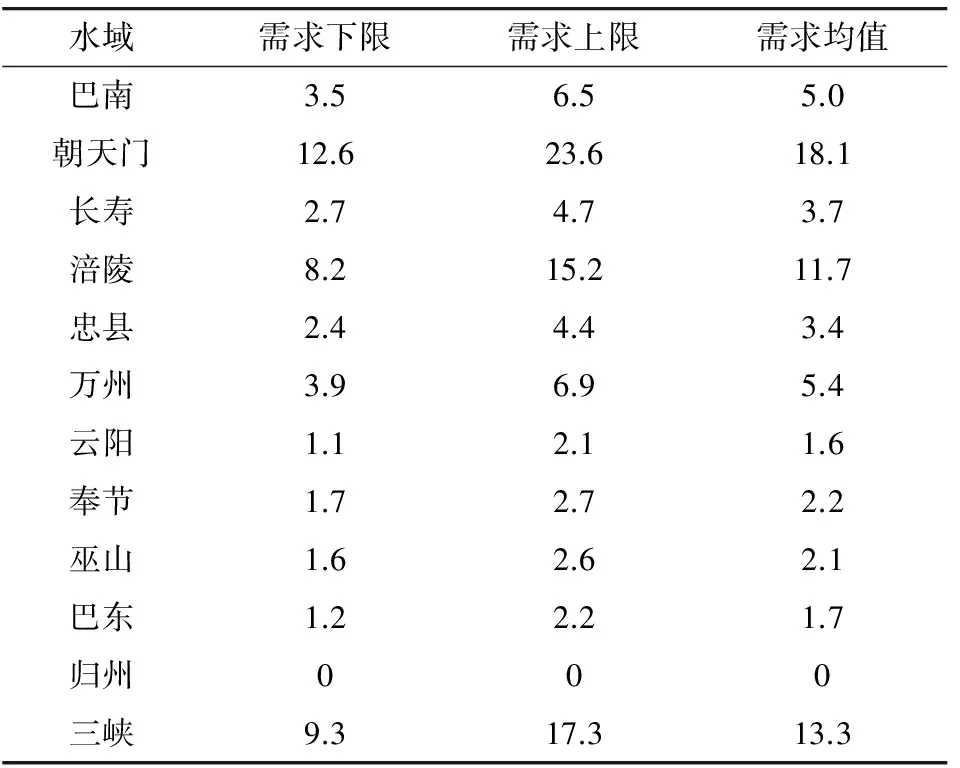
由式(1)可知，由于需求调整系数是不确定的，因此三峡库区水域应急资源需求是在一定范围内变动的。将表2中的三峡库区水域风险值、需求调整系数的上下限带入到式(1)中，可得到三峡库区各水域30 m级巡逻船需求如表3。

表3三峡库区各水域30m级巡逻船需求

Table3Demandforpatrolshipof30mclassinallwatersofThreeGorgesReservoirarea

2 三峡库区水上救助基地应急资源鲁棒优化配置模型建立

2.1 水上救助基地应急资源配置机理

三峡库区水上救助基地主要对覆盖半径为120～150 km的水域事故实施有效监管和救助，考虑水域需求多变，以及水上事故持续救援和重大事故救援情形，也可向服务范围以外的任一水域进行救援，但考虑救援的时效性和经济性，会优先选择离受灾水域距离较近，救援成本较低的救助基地调配巡逻船。三峡库区水上救助基地应急资源优化配置的实质就是确定各水上救助基地应急资源配置数量以满足各水域的不确定需求，实现救助基地应急资源的应急救助时效性和经济性最强。

三峡库区水上救助基地应急资源配置的网络拓扑结构如图1，图中Sj表示水上救助基地，Di表示受灾水域，当受灾水域发生事故时，应急资源由救助基地调运至受灾水域进行救援。

图1 三峡库区水上救助基地应急资源配置的网络拓扑图Fig. 1 Network topology of emergency resource allocation of water rescue base in Three Gorges Reservoir area

2.2 水上救助基地应急资源配置模型构建

水上事故发生后的72 h通常称为“黄金救援期”，应急资源首要任务是应急，时效性显得尤为重要，且应急资源配置量的过多或不足将造成应急资源闲置或缺失，影响资源配置效果。因此，三峡库区水上救助基地应急资源配置的目标为实现应急资源的救助时效性最强和闲置或缺失量最少。

三峡库区水上救助基地应急资源配置模型所涉及的参数如下：

Vj：水上救助基地应急资源配置的最大值；tij为应急资源从救助基地Sj调运至受灾水域Di的时间；di为受灾水域Di应急资源的需求量；xj为救助基地Sj配置应急资源数量；yij为应急资源从救助基地Sj调运至受灾水域Di的数量；zi为受灾水域Dj应急资源需求未满足时的补偿量。

综上，可得三峡库区水上救助基地应急资源配置模型如式(3)。

(3)

模型中，第1个目标函数表示实现三峡库区各水域应急资源闲置和缺失数量总和最小；第2个目标表示应急资源航行总时间最短以实现救援的时效性最强；第1个约束条件表示应急资源配置数量不能超过救助基地的容量限制；第2个约束条件表示从救助基地Sj调运至受灾水域应急资源不能超过救助基地的配置数量；第3个约束条件表示水上事故发生时，调运至受灾水域Di的应急资源需求可以得到满足；第4个约束条件表示救助基地应急资源的配置量、运送至各受灾水域的应急资源数量、受灾水域Dj应急资源需求未满足时应急资源的补偿量均为非负数。

通常情况下，应急资源的调运量和补偿量均随需求变化而变化，可表示成需求量的线性函数，如式(4)。

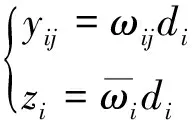
(4)

(5)

2.3 应急资源配置模型鲁棒对应的转化

通过上述分析，三峡库区水上救助基地应急资源配置模型可转化为式(6)。

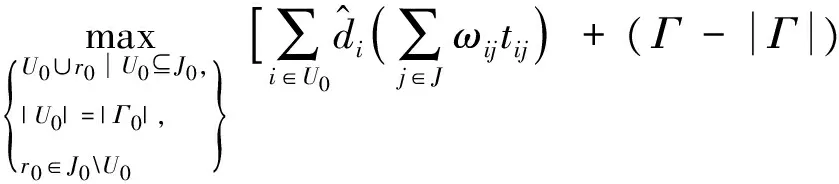
(6)

为将模型转化为容易求解的线性规划模型，分析如下最大化问题

(7)

由线性规划的对偶定理，原问题和对偶问题具有相同的最优值，因此可将式(7)的对偶问题转化为式(8)。

(8)

参考此对偶转化，三峡库区水上救助基地应急资源配置鲁棒优化模型如式(9)。

(9)

3 三峡库区水上救助基地巡逻船配置鲁棒优化配置方案分析

为验证三峡库区水上救助基地应急资源配置鲁棒优化模型的有效性和可行性，本研究以巡逻船配置为例，分析三峡库区各水上救助基地巡逻船的配置状况。

三峡库区航道较窄，为简化研究，将各水域中心与救助基地的航道里程距离视为巡逻船的航行距离，并假定应急救援船舶的速度为20 km/h，可得到巡逻船从救助基地航行至各水域的时间如表4。

表4 航行时间Table 4 The sailing time

将表3和表4中的数据带入到三峡库区水上救助基地应急资源配置鲁棒优化模型式(9)中，采用NSGA-II算法，并运用MATLAB7.0软件进行编程，假设需求扰动水平为20%，分析鲁棒控制参数(在0～12之间取值时，三峡库区救助基地巡逻船鲁棒优化配置方案如表5。

表5三峡库区水上救助基地巡逻船配置方案

Table5AllocationschemeofpatrolshipforwaterrescuebaseinThreeGorgesReservoirarea

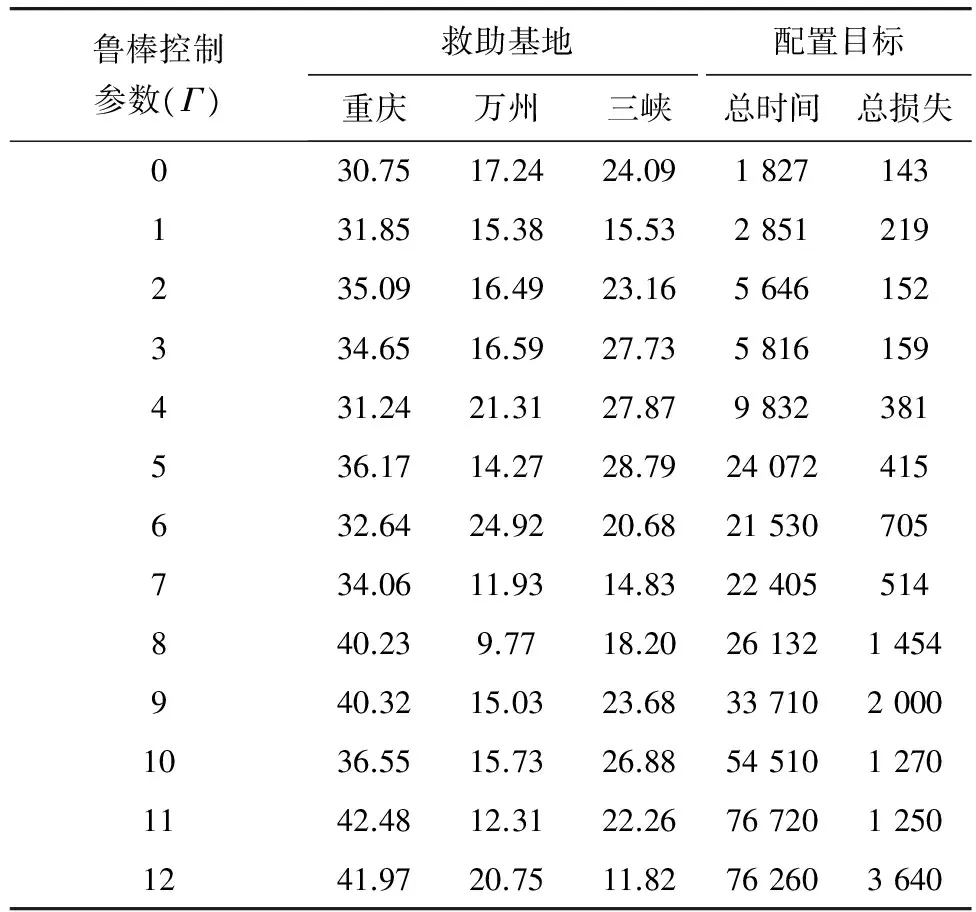
鲁棒控制参数Γ为扰动需求的数量，也是衡量决策者的风险偏好程度的指标，Γ的取值越大说明决策者在面对需求扰动时资源配置的态度越保守，反之则越冒险。Γ=12是鲁棒优化的特殊情形，认为所有需求点均表现出不确定性，是最保守的巡逻船配置情形。与最保守的巡逻船配置方案相比，当鲁棒控制参数Γ取值为1～11时，鲁棒优化配置方案能节约巡逻船配置总时间和总损失比例如图2，巡逻船鲁棒优化配置总量随鲁棒控制参数变化如图3。

图2 鲁棒优化配置效果Fig.2 The effect of robust optimization

图3 巡逻船鲁棒优化配置总量Fig. 3 Robust optimal allocation of total numbers of patrol ships

如图2，与传统保守配置方案相比，巡逻船鲁棒优化配置方案能节约配置总时间比例在45.05%～96.07%之间，能节约的配置总损失比例最大值为97.60%，当鲁棒控制参数Γ取值为1～7时，巡逻船配置总时间和总损失的节约尤其明显。

如图3，三峡库区巡逻船配置总量随着鲁棒控制参数呈马鞍形的变化趋势，随着鲁棒控制水平的增加，巡逻船配置总量逐渐增大，最大值为81艘，平均值为74艘，但当鲁棒控制水平趋于中值时，若重庆、万州、三峡3个救助基地分别配置34艘、12艘、15艘巡逻船，能实现巡逻船配置总量达到最低61艘。

4 结 论

笔者结合国家水上应急资源配备相关规定探讨了三峡库区应急资源的不确定需求，构建了三峡库区水上救助基地应急资源鲁棒优化配置模型，并从配置效果和投入两个角度对优化方案进行分析，得到以下主要研究结论：

1)鲁棒优化配置方案基本能实现配置效果优化，随着鲁棒控制水平(不确定需求总数)增加，优化配置方案能产生的配置总损失节约比例逐渐下降，总时间节约比例先下降后上升。

2)总体而言，鲁棒控制水平越高，为应对较多的需求扰动，需增配的巡逻船数量也越多，但当鲁棒控制参数位于中间值时，由于模型各参数、数据组合特点，巡逻船配置系统表现出较好的稳定性，此时，巡逻船的机动性较强，在总配置量较低的情况下能实现总配置损失和时间最小。

3)巡逻船鲁棒优化配置的总投入与配置效果并非正相关，在一定的鲁棒控制水平下，增加巡逻船投入总量能节约配置总时间和总缺失，但当鲁棒控制参数趋于中值时，巡逻船的过多投入会造成部分闲置损失，使得配置总损失不减反增，从而影响配置效果。

因此，盲目增加应急资源总投入不能提高资源配置效率，应急管理决策者可根据其风险偏好，选择合理的鲁棒控制参数，进而得到优化配置方案。本研究成果有助于决策者的风险偏好选择，实际应用意义较强，也可为内河相似水域应急资源配置提供决策参考。

[1] 许建国.应急资源需求周期性变化的选址与资源配置模型[J].运筹与管理,2008,17(1):11-17.

XU Jianguo. An optimal model of location and configuration for emergency resource based on varied periodic demands[J].OperationsResearchandManagement, 2008, 17 (1): 11-17.

[2] ZARDECKI A,MARKIN J T.Resource allocation optimization program for safeguards[C]//Fourth International Carnahan Conference on Security Technology, Albuquerque, New Mexico, 1994:1-10.

[3] FIEDRICH F, GEHBAUER F, RICKERS U.Optimized resource allocation for emergency response after earthquake disasters[J].SafetyScience, 2000,35(1): 41-57.

[4] TZENG G H, CHENG H J,HUANG T D. Multi-objective optimal planning for designing relief delivery systems [J].TransportationResearchPartELogistics&TransportationReview, 2007，43(6):673-686.

[5] LI Xiang, LI Yongjian.A Model on emergency resource dispatch under random demand and unreliable transportation[J].SystemsEngineeringProcedia, 2012, 5: 248 -253.

[6] 高学英.大规模应急救援资源布局与调度优化方法研究[D].吉林:吉林大学, 2012.

GAO Xueyin.TheLayoutandSchedulingOptimizationMethodsofLarge-scaleEmergencyReliefResources[D].Jilin: Jilin University, 2012.

[7] VLACHOS D, GEORGIADIS P, IAKOVOU E. A system dynamics model for dynamic capacity planning of remanufacturing in closed-loop supply chains [J].Computers&OperationsResearch, 2007，34(2): 367-394.

[8] 张玲.不确定需求下应急资源配置的鲁棒优化方法[J].系统科学与数学,2010,30(10):1283-1292.

ZHANG Ling.The robust optimization allocation of emergency resources under uncertain demand[J].SystemsScienceandMathematics,2010, 30(10): 1283-1292.

[9] SALMERON J, APTE A. Stochastic optimization for natural disaster asset prepositioning[J].ProductionandOperationsManagementSociety, 2010, 19(5): 561-574.

[10] SHEU J B. Dynamic relief-demand management for emergency logistics operations under large-scale disasters [J].TransportationResearchPartElogistics&TransportationReview, 2010,46(1) :1-17.

[11] SUN B, MA W, ZHAO H.A fuzzy rough set approach to emergency material demand prediction over two universes [J].AppliedMathematicalModeling, 2013, 37(10): 7062-7070.

[12] CAIN P M. Modeling and forecasting brand share: A dynamic demand system approach [J].InternationalJournalofResearchinMarketing, 2005,22(2):203-220.

[13] 左静,帅斌.铁路非常规突发事件应急救援决策方法研究[J].交通运输系统工程与信息,2014,14(6):120-125.

ZUO Jing,SHUAI Bin.Decision-making method for unconventional railway emergency rescue[J].JournalofTransportationSystemsEngineeringandInformationTechnology, 2014, 14(6): 120-125.

EmergencyResourcesAllocationofThreeGorgesReservoirAreaBasedonRobustOptimization

YANG Jiaqi1, ZHANG Wenfen1, 2

(1.School of Transportation, Wuhan University of Technology, Wuhan 430063, Hubei,P.R.China; 2.Intelligent Transportation Systems Research Center, Wuhan University of Technology, Wuhan 430063, Hubei,P.R.China)

According to maritime jurisdiction scope, the Three Gorges Reservoir area is divided into several waters. Considering the relevant regulations of the state and the risk of waters, the uncertain demand of emergency resources of Three Gorges Reservoir area was analyzed. On the basis of exploring the emergency resource allocation mechanism of water rescue base, the emergency resource allocation robust optimization model of Three Gorges Reservoir rescue base was established to minimize the total loss and time of the emergency resource allocation. Taking patrol ships as an example, the optimal allocation scheme of patrol ship under various uncertain demands was obtained. The findings show that: the robust optimal allocation scheme can basically achieve the overall optimization disposition effect. When the total number of disturbance demand is in the middle value, the patrol ship allocation system of the water rescue base in the Three Gorges Reservoir area shows better stability. At the same time, the maneuverability of the patrol ship is stronger, and the total number of patrol ships is the lowest. The research results are helpful for decision-makers’ choice of risk preference and have stronger practical significance, which can also provide reference for the allocation of emergency resources in similar waters of inland rivers.

traffic and transportation engineering;Three Gorges Reservoir area; uncertain demand; robust optimization; emergency resources allocation

10.3969/j.issn.1674-0696.2017.11.14

2016-06-30；

2016-09-19

国家自然科学基金项目(51279153)

杨家其(1964—)，男，湖北鄂州人，教授，博士研究生导师，主要研究方向：港口航运与综合物流。E-mail：styjq@whut.edu.cn。

X913.4；U491

A

1674-0696(2017)11-071-07

(责任编辑：朱汉容)