月前日负荷曲线的概率预测和随机场景模拟

颜 伟, 李 丹, 朱继忠, 任洲洋, 赵 霞, 余 娟

(1. 重庆大学电气工程学院, 重庆市 400044; 2. 南方电网科学研究院, 广东省广州市 510080)

月前日负荷曲线的概率预测和随机场景模拟

颜 伟1, 李 丹1, 朱继忠2, 任洲洋1, 赵 霞1, 余 娟1

(1. 重庆大学电气工程学院, 重庆市 400044; 2. 南方电网科学研究院, 广东省广州市 510080)

针对现有中长期日负荷曲线预测方法大多为点预测,难以满足电力系统不确定性分析的不足,提出了一种基于因子分析和神经网络分位数回归的月前日负荷曲线概率预测和随机场景模拟方法。采用因子分析技术,在保留日内负荷时序相关性的前提下,对日负荷序列向量降维;提取出少数相互独立的负荷公共因子作为预测变量,以日气象因素、星期类型和前一日公共因子值为输入特征,建立计及相邻日负荷相关性的神经网络分位数回归概率预测模型;以此为基础,利用中期气象预报信息,逐日预测和模拟未来30日的负荷曲线,并生成未来月负荷曲线的随机模拟场景。实际算例结果验证了所提概率预测方法的准确性和高效性,其生成的日负荷曲线模拟场景更好地体现了负荷的时序相关性,能为调度人员提供更准确、全面的月前负荷预测信息。

负荷概率预测;日负荷曲线; 时序相关性; 因子分析; 神经网络分位数回归; 气象因素

0 引言

当前,随着电力体制改革不断深化,电力市场交易、分布式能源接入和新型负荷等不确定性因素不断增加,对电网调度运行水平提出了更高要求。国家电网公司和南方电网公司在“十三五”规划中,均明确将中长期时间尺度下的调度和市场交易计划优化以及安全校核作为规划重点内容之一[1-2]。

作为中期电力调度和市场交易的基础,月度负荷曲线预测和模拟至关重要[3]。由于负荷的日周期性,日负荷曲线预测是月负荷曲线预测的基础。传统的中长期日负荷曲线预测方法一般为点预测[4-5],即给出确定的预测负荷时间序列。随着电动汽车等新型负荷逐渐增加[6]、分布式冷热电联供系统不断推广[7],电力负荷不确定性将更加明显,传统确定性负荷预测会使决策工作面临一定程度风险,在决策时考虑电力需求的不确定性,开展负荷概率预测更符合客观需求[8]。

目前,概率预测方法多用于短期负荷预测,有区间估计法[9]、核密度估计法[10]和分位点回归法[11-14]等。其中前两种方法多通过历史负荷确定性预测误差的统计规律计算预测区间对应的概率置信水平或估计概率密度函数;分位点回归法则直接考察不同概率分位点水平下解释变量和被解释变量之间的关系,是近年来负荷概率预测文献关注的热点[11-14]。如文献[11]和文献[12]分别以多个独立的专家预测模型和多元线性回归模型得到的负荷点预测结果集合为基础,采用线性分位数回归得到预测负荷的概率分布区间。然而线性形式的负荷点预测模型和分位数回归模型,难以分析解释变量对预测负荷的非线性范式影响。神经网络分位数回归(quantile regression neural network,QRNN)法将神经网络强大的非线性处理能力与分位数回归技术相结合,为分析解释变量对响应变量的非线性影响提供了一个有效工具[15-16],具有预测精度高、预测信息稳定等优点。如文献[13]运用径向基函数(RBF)QRNN方法,输入前11天各时刻的历史负荷数据,获得了预测日对应时刻负荷的概率分布函数。文献[14]将日最高气温预测值信息作为输入特征之一,运用反向传播(BP)QRNN方法获得预测日最大负荷的概率密度函数,算例结果表明考虑温度因素能有效提高负荷概率预测精度。随着气象预测技术的发展,国内部分公共气象网站已能提供未来30日的中期气象预报[17],包含天气类型、极值气温、风向和风力等日气象预测信息。虽然中期气象预测不及短期数值气象预测准确,但相对于不考虑气象预测信息的现有中期负荷预测方法,引入预测时段特定的气象预测信息能在整体上改善中期负荷预测精度。

相较于短期负荷预测,以提前一个月为代表的中期日负荷曲线预测规模更大、时间跨度更长。负荷曲线不仅受当日气象因素和日类型等短期因素影响,还受到经济发展水平、用电结构和用电行为等中长期因素影响,使得日内不同时刻负荷之间、相邻日同时刻负荷之间都具有很强的相关性。如果直接对各时刻负荷单独建立概率预测模型,不仅预测变量数量庞大,而且无法计及时序负荷间的相关关系。因子分析是一种通过降维技术化简多维向量的多元统计方法[18],它提取出彼此独立的少数潜在公共因子,使其尽量完整保留原始变量共性信息的同时,很好保留原始变量之间的相关关系。在电力系统中,它常被用于实时电价、风电等具有复杂相关关系多维向量的降维[19-20]。

基于以上分析,本文提出一种基于因子分析和QRNN的月前日负荷曲线概率预测和随机场景模拟方法。首先,采用因子分析技术对日内24维小时级负荷序列向量降维化简,用因子荷载矩阵解释日内不同时刻负荷的时序相关性,用少数相互独立的负荷公共因子向量解释日内负荷共性信息。然后,将负荷公共因子作为预测变量,计及相邻日对应负荷公共因子之间的相关性,以气象因素、星期类型以及前一日公共因子值为输入,分别建立各负荷公共因子的QRNN条件概率模型。以此为基础,利用中期气象预报信息,逐日预测各公共因子的连续概率分布曲线,通过模拟服从预测分布的公共因子和各时刻特殊因子,并代入因子模型逐日还原负荷预测曲线,生成未来月负荷曲线的随机模拟场景。实际算例结果表明,本文方法不仅提高了月前日负荷曲线概率预测精度和预测效率,而且生成的日负荷曲线场景能更准确地模拟负荷时序相关性,为月度概率优化调度、概率风险分析和决策提供信息支撑。

1 日负荷曲线的因子分析模型

1.1 24维标准负荷序列向量

将原始日负荷曲线标准化,得到24维标准负荷序列向量P:

(1)

式中:D为样本观测日的总天数;Pi,d为第d日时刻i负荷标准值。

(2)

式中:μi和Si分别为时刻i原始负荷的样本均值和样本标准差。

1.2 日负荷曲线的因子分析模型

24维标准负荷序列向量P=[P1,…,Pi,…,P24]T因子分析的一般模型为[18]:

P=AF+ε

(3)

基于历史观测样本,式(3)所示模型中的因子载荷阵A和特殊方差阵D可采用主成分法估计,具体如下:

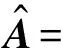
(4)

(5)

(6)

(7)

式中:Pd为24×1阶的第d日负荷标准值向量。

以2014年5月—7月期间的重庆地区小时级系统负荷观测样本为例,对标准化处理之后的日负荷标准值曲线进行因子分析。首先,计算观测样本中24时刻标准化负荷的协方差矩阵S,并提取S的特征值,当选择r=2时公共因子累计贡献率已达98.87%(前2个公共因子贡献率分别为95.47%和3.4%)。附录A图A1给出了2个负荷公共因子对应的估计载荷aij(i=1,2,…,24;j=1,2)的图形化表示。图中公共因子1对各时刻负荷的载荷权重均为正值,且值较稳定;而公共因子2对不同时刻负荷的载荷权重有较大差别。这意味着公共因子1基本反映了日内负荷整体水平,公共因子2则反映了负荷曲线的形状特征,体现日内各时刻负荷值的差异。

以上因子分析的实例表明,以少数r维负荷公共因子代替原始24维负荷作为日负荷曲线的预测变量,能在尽可能保留原始日负荷曲线最大共性信息量的条件下,减少预测变量个数。而且相较24时刻负荷变量之间复杂的相关关系,r维负荷公共因子之间相互独立,预测模型更为简单。这对规模庞大且关系复杂的日负荷曲线而言,能有效提高预测效率。

2 日负荷公共因子的QRNN预测

2.1 QRNN模型

2000年,Taylor提出QRNN模型[15],利用神经网络的非线性核函数,分析在不同分位点下解释变量x1,x2,…,xK对响应变量y的非线性影响。

QRNN模型使用三层BP感知器神经网络。解释变量X=[x1,x2,…,xK]为输入层,本文中对应与负荷密切相关的气象因素、星期类型和前一日的对应公共因子值等输入特征。响应变量yj为输出层,本文中对应负荷公共因子fj(j=1,2,…,r)。隐含层包含J个节点,隐含层转换函数选择双曲正切函数,从输入层到输出层之间表现出如下的非线性关系[16]:

(8)

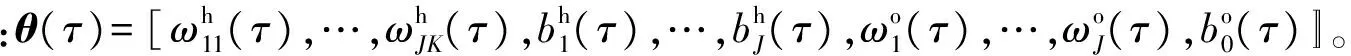
2.2 模型参数估计

对式(8)所示QRNN模型中参数θ(τ)的估计,旨在最小化如下形式的损失函数:

Qyd,j(τ))](yd,j-Qyd,j(τ))

(9)

式中:yd,j表示第d个样本日第j个公共因子的值;Qyd,j(τ)表示将第d个样本日的解释向量Xd代入式(8)所示模型得到的第j个公共因子的τ条件分位数。

I(·)为指示函数,有

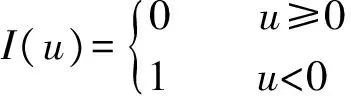
(10)

Wmonth,d为指数形式的时间权重,按样本日距离预测月时间趋势性“近大远小”的原则,体现不同历史样本日对损失函数的影响,其表达式如下:

Wmonth,d=anmonth,d-1

(11)

式中:nmonth,d为样本日d所在月距离预测月的月份期数,最远期的时间权重最小,最近期Wmonth,d=a0=1最大,其中a表示根据预测误差确定的时间权重参数。

为避免QRNN模型陷入过度拟合,在目标函数中増加一个惩罚项[16]。此时,QRNN模型的参数估计转化为下列优化问题:

(12)

实例中,惩罚参数ρ和隐含层节点数目J的最优取值可以通过式(13)所示的赤池信息量准则(Akaike information criterion,AIC)来确定[21]。

AIC(ρ,J)=

(13)

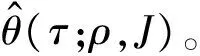
2.3 负荷公共因子的概率密度预测

(14)

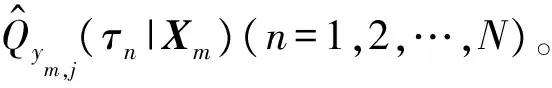
3 月前日负荷曲线随机场景生成

步骤1:设预测日编号m=0。

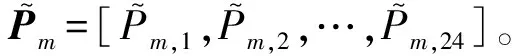
步骤6:重复步骤1至5,直至生成指定个数T组未来月负荷曲线随机场景。

未来月负荷曲线随机场景结果可直接用于月度发电调度和电力市场交易决策制定时的蒙特卡洛模拟,以评估由负荷随机性引发的系统安全风险和发购电成本概率分布。由大量的负荷曲线随机场景,也可提取出各时刻负荷的模拟样本,用于估计对应时刻负荷的边际概率分布或置信区间。

4 算例分析

4.1 算例描述

采用本文方法对2014年8月1日至30日重庆地区系统负荷进行月前日负荷曲线概率预测和场景模拟,观测样本为同年5月—7月期间的小时级负荷、日气象因素和星期类型。解释变量有天气类型x1、日最高气温x2、日最低气温x3、星期类型x4和前一日的对应公共因子值x5。其中,观测样本的气象数据来自历史气象记录,预测日的气象数据来自公共气象预测网站提供的未来30日气象预测数据[17]。由于不同类型的解释变量有不同的量纲和取值范围,所有解释变量值都事先量化并标准化到[0,1]区间。

经因子分析,公共因子维数r确定为2。时间权重参数a=0.5。选择全部观测日样本(92组)进行训练,神经网络训练迭代次数设为1 000,选取分位点区间为0.000 1～0.999 9,间隔0.05。BP神经网络输入层节点数为5,输出层为1,通过式(13)的AIC准则确定最优惩罚参数ρ为0.1,各负荷公共因子在不同分位点下的最优隐含层节点数见附录B表B1。

4.2 概率预测精度评价指标

概率预测效果主要从两方面评价:一是概率预测结果的可靠性,即实际值落入预测区间内的概率应尽可能接近事先给定的置信度;二是预测区间应尽量窄,不确定信息尽量集中。本文选用下列3种概率预测评价指标来分析预测结果[22]。

1)可靠性指标

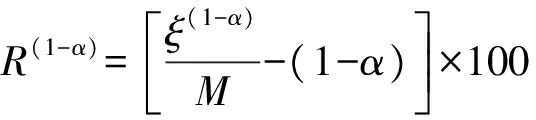
(15)

式中:R(1-α)为置信度1-α下的可靠性指标值;M为测试样本的个数;ξ(1-α)为在置信度1-α下实际负荷值落入预测置信区间的个数。

2)区间平均宽度指标

(16)

式中:I(1-α)为置信度1-α下的负荷区间平均宽度;θi(1-α)为第i个测试样本在置信度1-α下负荷预测区间上界和下界之差。

3)点预测值平均绝对百分比误差(mean absolute percentage error,MAPE)指标

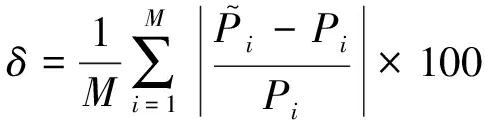
(17)

上述3个评价指标中,可靠性指标评价置信区间可信程度,其绝对值越小,可信程度越高;区间平均宽度指标评价预测结果聚集不确定信息的能力,其值越小越好。点预测值MAPE误差δ则评价点预测结果与实际值的相对偏差,值越小越好。

4.3 月前日负荷预测曲线随机场景生成结果

附录B图B1以8月1日—7日为例给出了本文方法模拟的20组日负荷预测曲线与实际曲线的对比,结果显示出本文方法生成的月前日负荷预测曲线随机场景与实际负荷曲线变化趋势十分相似。

由于模拟计算量不大,很容易将场景数提高到数千甚至数万。采用本文方法模拟生成1×104组月前日负荷预测曲线随机场景,并根据各时刻负荷模拟样本值分布,统计以众数为中心的10%～90%置信度下的置信区间。图1给出了同一时期20%,70%,90%置信度下预测负荷置信区间、众数点预测值与实际值的对比。

图1 不同置信度下日负荷曲线概率预测结果Fig.1 Probabilistic forecasting results of daily load curve with different confidence levels

图1中实际负荷曲线大部分位于90%和70%置信度的置信区间内,部分落入20%置信度的置信区间内,而且以公共因子概率众数为点预测结果得到的负荷预测曲线与实际曲线变化趋势基本一致。

4.4 与其他负荷概率预测方法的对比分析

将本文方法分别与文献[10]的预测误差核密度估计方法和文献[13]的分时刻QRNN预测方法进行对比。其中,文献[10]以动态自适应RBF神经网络预测的负荷点预测结果为基础,叠加对应时段和负荷值分区条件下预测误差的随机分布,获得预测负荷的概率分布。其中预测误差概率分布由历史负荷预测误差通过非参数核函数估计得到。采用RBF神经网络对算例中各时刻负荷进行点预测时,解释变量为预测日的气象因素和星期类型。文献[13]不经过因子分析,直接对各时刻负荷进行QRNN概率预测。具体又分为考虑气象因素和不考虑气象因素两种情况,其区别在于前者的解释变量包含气象因素和星期类型,而后者的解释变量仅包含星期类型。分时刻QRNN预测方法的模型结构确定方式和参数估计方法与本文方法相同。

表1和图2至图4分别给出了4种预测方法的预测时间、点预测结果、不同置信度下的预测精度指标和模拟负荷曲线场景的自相关系数均值对比。其中预测时间采用MATLAB程序中时间函数进行监测(计算机为酷睿i5双核2.4 GHz,内存4 GB)。

表1 4种概率预测方法的预测结果Table 1 Results of four probabilistic prediction methods

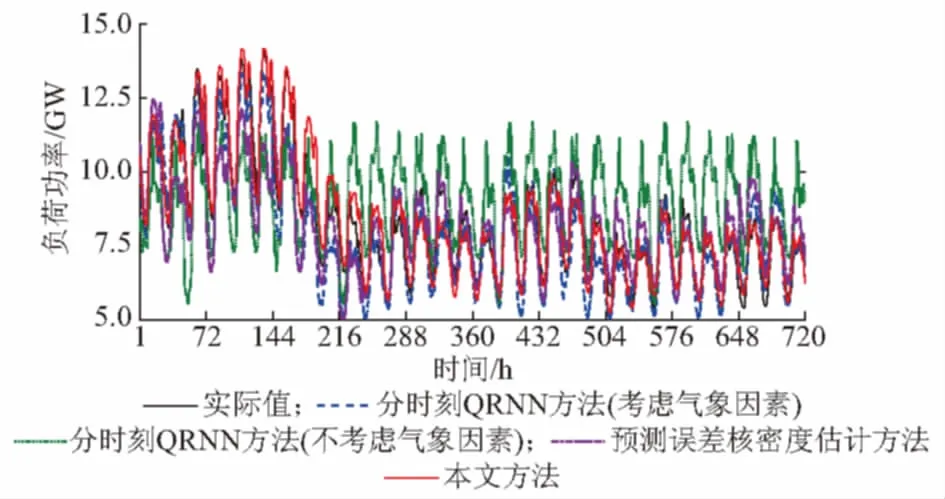
图2 月负荷曲线的点预测结果Fig.2 Point prediction results of monthly load curve

图3 概率预测评价指标对比Fig.3 Comparison of evaluation indices for probability forecasting

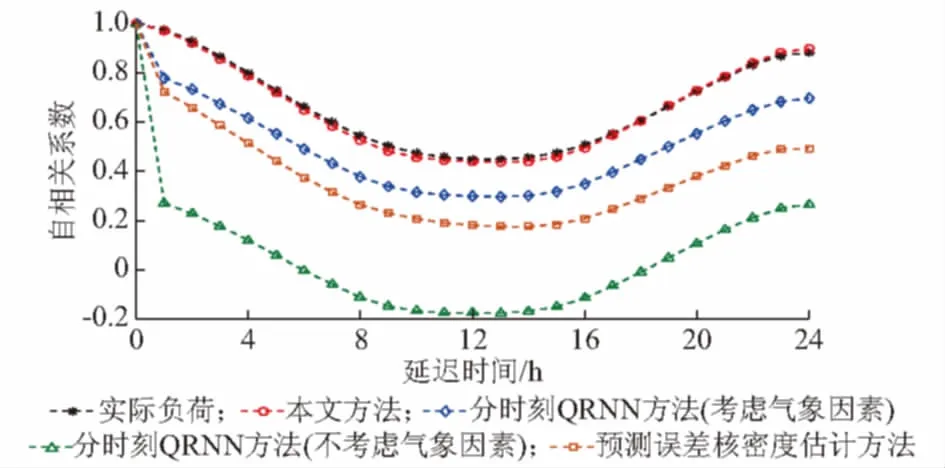
图4 模拟负荷曲线场景的自相关系数对比Fig.4 Autocorrelation coefficient comparison in simulated load curve scenarios

从图2和图3可以直观地看出,无论是众数点预测结果,还是各置信度下的可靠性和区间平均宽度,不考虑气象因素的分时刻QRNN预测方法在4种方法中预测效果最差。这表明引入中期气象预测信息可以明显提高预测精度。

将本文方法与同样考虑气象因素的分时刻QRNN预测方法和预测误差核密度估计方法进行对比。从表1、图2和图3可以看出:在点预测MAPE方面,3种预测方法点预测结果的预测误差均未超过11%,但本文方法的预测误差比分时刻QRNN预测方法小2.61%,比预测误差核密度估计方法小4.32%;在可靠性方面,本文方法与分时刻QRNN预测方法差别不大,大多保持在±2%以内,预测误差核密度估计方法略差;在区间平均宽度方面,分时刻QRNN预测方法和预测误差核密度估计方法相差不大,而本文方法比这两种方法窄了约50%。在预测时间成本方面,预测误差核密度估计方法所需时间最少,其次是本文方法,预测时间仅为分时刻预测方法的1/15。这是因为本文方法只需建立2个负荷公共因子的QRNN模型,而分时刻QRNN预测方法则需建立24个时刻负荷的QRNN模型,建模和模型参数估计时间都增加了十多倍。以上预测结果对比表明:与同样考虑气象因素的分时刻QRNN负荷概率预测方法相比,本文方法可以在不明显降低置信区间可信度的基础上,获得更高的预测效率和更窄的区间宽度,提高预测结果聚集不确定信息的能力;另外,由于预测误差核密度估计方法的负荷概率分布建立在全部历史预测误差统计分析的基础上,无法体现出预测日特定的日输入特征对负荷随机性的影响,而本文方法直接研究日输入特征与随机负荷分位数之间的非线性映射关系,分析其对负荷概率分布的影响,能显著改善概率预测精度。

相较另外3种负荷概率预测方法,图4中本文方法得到的模拟负荷曲线自相关系数与实际时序负荷更加接近。这是因为分时刻QRNN预测方法和预测误差核密度估计方法单独建立各时刻负荷或负荷预测误差的概率预测模型,负荷或负荷预测误差的抽样值虽然能保证对应时刻下的概率分布,但无法保证不同时刻之间的时序相关性,而本文方法通过因子模型中公共因子与各时刻负荷的变换关系,较好地保留了日内负荷时序相关关系,同时在负荷公共因子概率预测模型中引入前一日公共因子为输入特征,体现了相邻日负荷间的相关关系。

5 结论

本文引入因子分析技术对复杂的日内小时级负荷时间序列向量进行降维化简,提取出相互独立的日负荷公共因子为直接预测变量,建立考虑相邻日负荷相关性的QRNN条件概率模型,并以此为基础,利用中期气象预测信息实现月前日负荷曲线的概率预测和随机场景模拟。

实际算例结果表明:引入中期气象预测信息能有效提高预测精度;与分时刻QRNN负荷概率预测方法相比,本文方法能提高预测效率和预测结果聚集不确定信息的能力,其预测精度也高于传统的点预测值叠加随机预测误差的负荷概率预测方法;而且模拟生成的未来月日负荷曲线场景更好地体现了负荷的时序相关性。由于中期天气预测精度会随着提前时间增长逐渐下降,在本文方法的实际应用中,可根据每日更新的中期天气预报信息滚动预测,并与短期预测和超短期预测相配合,进一步改善月前日负荷曲线的预测精度。

本文方法模拟的月前日负荷预测曲线随机场景可用于概率优化调度、概率风险分析和决策等诸多方面。由于目前国内外负荷概率预测方法的研究尚处于起步阶段,本文方法在概率预测结果评价标准、时间权重和公共因子个数等模型参数对预测结果影响等方面有待进一步深入研究。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 国家电网公司调度中心.国家电网公司“十三五”调控运行规划[R].北京:国家电网公司调度中心,2016.

[2] 广东电网有限责任公司.中国南方电网“十三五”创新驱动行动计划——系统运行专业分册[R].广州:广东电网有限责任公司,2016.

[3] 赵儆,康重庆,葛睿,等.电力市场中多日负荷曲线的预测[J].电力系统自动化设备,2002,22(9):31-33.

ZHAO Jing, KANG Chongqing, GE Rui, et al. Multi-day load curve forecasting in electricity market[J].Electric Power Automation Equipment, 2002, 22(9): 31-33.

[4] 许梁,孙涛,徐箭,等.基于函数型非参数回归模型的中长期日负荷曲线预测[J].电力自动化设备,2015,35(7):89-94.

XU Liang, SUN Tao, XU Jian, et al. Mid-and long-term daily load curve forecasting based on functional nonparametric regression model[J]. Electric Power Automation Equipment, 2015, 35(7): 89-94.

[5] 李萌,程浩忠,杨宗麟,等.采用分形插值的典型日负荷曲线改进预测方法[J].电力系统及其自动化学报,2015,27(3):36-41.

LI Meng, CHENG Haozhong, YANG Zonglin, et al. Improved forecasting method of typical daily load curve based on fractal interpolation[J]. Proceedings of the CSU-EPSA, 2015, 27(3): 36-41.

[6] 杨波,陈卫,文明浩,等.电动汽车充电站的概率负荷建模[J].电力系统自动化,2014,38(16):67-73.DOI:10.7500/AEPS20131027001.

YANG Bo, CHEN Wei, WEN Minghao, et al. Probabilistic load modeling of electric vehicle charging stations[J]. Automation of Electric Power Systems, 2014, 38(16):67-73. DOI: 10.7500/AEPS20131027001.

[7] 马瑞,李文晔,李晅,等.分布式冷热电联供系统负荷随机模糊建模[J].电力系统自动化,2016,40(15):53-58.DOI:10.7500/AEPS20151021001.

MA Rui, LI Wenye, LI Xuan, et al. Random fuzzy for load distributed combined cooling, heating and power system[J]. Automation of Electric Power Systems, 2016, 40(15): 53-58. DOI: 10.7500/AEPS20151021001.

[8] HONG T, FAN S. Probabilistic electric load forecasting: a tutorial review [J]. International Journal of Forecasting, 2016, 32(3): 914-938.

[9] 方仍存,周建中.应用聚类算法和混沌理论的短期负荷概率性区间预测[J].电网技术,2010,34(11):65-69.

FANG Rengcun, ZHOU Jianzhong. Probabilistic interval forecasting of short-term load on the basis of clustering algorithm and chaos theory[J]. Power System Technology, 2010, 34(11): 65-69.

[10] 周建中,张亚超,李清清,等.基于动态自适应径向基函数网络的概率性短期负荷预测[J].电网技术,2010,34(3):37-41.

ZHOU Jianzhong, ZHANG Yachao, LI Qingqing, et al. Probabilistic short-term load forecasting based on dynamic self-adaptive radial basis function network[J]. Power System Technology, 2010, 34(3): 37-41.

[11] HONG T, MACIEJOWSKA K, NOWOTARSKI J, et al. Probabilistic load forecasting via quantile regression averaging of independent expert forecasts[R]. Wroclaw, Poland: Hugo Steinhaus Center, Wroclaw University of Technology, 2014.

[12] LIU B, NOWOTARSKI J, HONG T, et al. Probabilistic load forecasting via quantile regression averaging on sister forecasts[J]. IEEE Trans on Smart Grid, 2018, 8(2): 730-737.

[13] 何耀耀,许启发,杨善林,等.基于RBF神经网络分位数回归的电力负荷概率密度预测方法[J].中国电机工程学报,2013,33(1):93-98.

HE Yaoyao, XU Qifa, YANG Shanlin, et al. A power load probability density forecasting method based on RBF neural network quantile regression[J]. Proceedings of the CSEE, 2013, 33(1): 93-98.

[14] 何耀耀,闻才喜,许启发,等.考虑温度因素的中期电力负荷概率密度预测方法[J].电网技术,2015,39(1):176-181.

HE Yaoyao, WEN Caixi, XU Qifa, et al. A method to predict probability density of medium-term power load considering temperature factor[J]. Power System Technology, 2015, 39(1): 176-181.

[15] TAYLOR J W. A quantile regression neural network approach to estimating the conditional density of multi-period returns[J]. Journal of Forecasting, 2000, 19(4): 299-311.

[16] CANNON A J. Quantile regression neural networks: implementation in R and application to precipitation downscaling[J]. Computers & Geosciences, 2010, 37(9): 1277-1284.

[17] 中国气象局.中国天气网:城市天气预报30天,重庆,2014[EB/OL].[2014-08-01].http://www.tianqi.com/.

[18] BASILEVSKY A. Statistical factor analysis and related methods: theory and applications[M]. New York, USA: Wiley, 1994: 351-352.

[19] GARCIA-MARTOS C, RODRIGUEZ J, SANCHEZ M J. Forecasting electricity prices by extracting dynamic common factors: application to the Iberian market[J]. IET Generation Transmission & Distribution, 2012, 6(1): 11-20.

[20] GARCIA-MARTOS C, SANCHEZ M J. A dynamic factor model for mid-term forecasting of wind power generation[C]// 10th International Conference on the European Energy Market (EEM), May 27-31, 2013, Stockholm, Sweden: 7p.

[21] 许启发,陈士俊,蒋翠侠,等.极端Var风险测度的新方法:QRNN+POT[J].系统工程学报,2016,31(1):33-44.

XU Qifa, CHEN Shijun, JIANG Cuixia, et al. A new method for extreme value at risk measure: QRNN+POT[J]. Journal of Systems Engineering, 2016, 31(1): 33-44.

[22] SIDERATOS G, HATZIARGYRIOU N D. Probabilistic wind power forecasting using radial basis function neural networks[J]. IEEE Trans on Power Systems, 2012, 27(4): 1788-1796.

Probabilistic Forecasting and Stochastic Scenario Simulation of Month-ahead Daily Load Curve

YANWei1,LIDan1,ZHUJizhong2,RENZhouyang1,ZHAOXia1,YUJuan1

(1. School of Electrical Engineering, Chongqing University, Chongqing 400044, China; 2. Electric Power Research Institute, China Southern Power Grid, Guangzhou 510080, China)

The existing forecasting methods of medium and long term load curves are mostly point prediction methods, which can hardly make up for the inadequacy of the uncertainty analysis of power systems. For this reason, a probabilistic forecasting and stochastic scenario simulation approach based on factor analysis and quantile regression neural network (QRNN) is proposed. By means of the factor analysis method, the dimensionality of daily load time series vector is reduced without sacrificing correlation of intraday load time series. A few independent load common factors are extracted and used as predictor variables. With the daily weather factors, weekday type and the corresponding common factor of the previous day as inputs, the QRNN models of load common factors considering the load correlation between adjacent days are developed. Based on these probabilistic forecasting models, the load curves of next 30 days are predicted and simulated day by day, and stochastic scenarios of future month load curve are generated finally. The accuracy and high efficiency of the proposed approach have been verified by the results of an actual example. The correlation of load time series generated by the proposed approach is more accurate, being able to provide more accurate and all-round month-ahead load forecast information to system operators.

This work is supported by National Natural Science Foundation of China (No. 51677012) and Natural Science Foundation of Chongqing Science and Technology Commission (No. cstc2013jcyjA90001).

load probabilistic forecasting; daily load curve; autocorrelation of time series; factor analysis; quantile regression neural network (QRNN); weather factors

2016-09-08;

2017-02-28。

上网日期: 2017-05-23。

国家自然科学基金资助项目(51677012);重庆市科委自然科学基金资助项目(cstc2013jcyjA90001)。

颜 伟(1968—),男,博士,教授,博士生导师,主要研究方向:电力系统优化运行与控制。E-mail：cquyanwei@cqu.edu.cn

李 丹(1980—),女,通信作者,博士研究生,工程师,主要研究方向:电力系统概率分析、新能源发电和电力系统优化运行。E-mail: lucy2140@163.com

朱继忠(1966—),男,博士,教授,博士生导师,国家“千人计划”特聘专家,主要研究方向:电力系统分析运行与控制、电力市场、智能电网和可再生能源应用。E-mail: zhujz@csg.cn

(编辑 蔡静雯)