考虑容量及电压约束的高压配电网可靠性快速评估算法

昝贵龙, 王主丁, 刘念祖, 吴延琳, 王晓博, 王国亮

(1. 输配电装备及系统安全与新技术国家重点实验室(重庆大学), 重庆市 400044; 2. 国网郑州供电公司, 河南省郑州市 450000; 3. 国网陕西省电力公司经济技术研究院, 陕西省西安市 710000)

考虑容量及电压约束的高压配电网可靠性快速评估算法

昝贵龙1, 王主丁1, 刘念祖2, 吴延琳3, 王晓博2, 王国亮2

(1. 输配电装备及系统安全与新技术国家重点实验室(重庆大学), 重庆市 400044; 2. 国网郑州供电公司, 河南省郑州市 450000; 3. 国网陕西省电力公司经济技术研究院, 陕西省西安市 710000)

鉴于目前高压配电网可靠性评估研究较少,文中提出一种考虑容量及电压约束的可靠性评估快速混合算法。基于高压配电网分区供电特点,将大规模电网转换为多个小规模电网;提出将线路允许电压损耗转化为相应的容量约束,之后的算法不再考虑电压约束;提出基于虚拟初始闭环潮流的元件冗余容量进行容量约束保守校验,快速筛选出部分不受容量约束的故障状态。该算法将网流法引入高压配电网可靠性评估,利用最大流模型进行容量约束详细校验,并采用消圈法进行最小切负荷快速计算。算例结果表明,在满足工程计算精度情况下,高压配电网分区策略加上保守和详细容量校验可减少计算量,具有实用价值。

高压配电网; 可靠性评估; 电压约束; 容量约束; 网流法; 最小切负荷

0 引言

高压配电网通常指电压等级为35～110 kV的配电网[1],是连接输电网和中压配电网的核心枢纽,其可靠性对于电网的正常运行具有重要影响。高压配电网实行分区供电,各供区分区相对独立,一般情况下开环运行,仅少数情况下闭环运行[2]。

主网通常环网运行,元件故障后开断潮流的方向通常不具有唯一性,考虑容量电压约束一般需要进行潮流计算。基于交流潮流的非线性规划得到的切负荷结果比较精确,但交流潮流计算量大,非线性规划求解稳定性较差[3]。文献[4]利用直流潮流建立了线性规划切负荷模型,利用单纯形法求解线性规划的计算时间可能为网络规模的指数时间[5],而且不能确保计算稳定性。

中压配电网通常开环运行,可靠性评估中一般可以采用简化潮流计算。部分研究采用等值或聚类方法简化潮流计算,但仍需调用大量完整潮流[6-7]。文献[8-9]基于因元件停运负荷转供路径的潮流变化,提出了近似计算相应的容量和电压允许负荷转供率。文献[10]提出一种仅对潮流变化较大的线路和节点进行潮流估算的方法。文献[8-10]利用潮流估计避免了完整的潮流计算,但仅考虑负荷单一方向转供,且没有进行切负荷优化。

不同于主网,高压配电网大多开环运行;不同于中压配电网,高压配电网通常需要考虑二阶故障,还可能需要考虑多个方向的负荷转供。利用网流代替直流或者交流潮流可以避免直接计算系统潮流提高计算效率[11],同时也能方便地考虑多个转供通道。网流模型忽略了基尔霍夫第二定律[12],但对高压配电网功率分布影响较小,因为对于大多数开环运行的弱环高压配电网,不存在基尔霍夫第二定律约束。

本文提出了一种考虑容量及电压约束的高压配电网可靠性快速评估方法及其流程。根据高压配电网分片运行的特点将电网分区,元件故障时仅在所在分区进行网络搜索;将估计的各线路允许电压损耗转化为相应的容量约束;基于初始闭环潮流,根据元件容量冗余对故障状态进行容量约束保守校验;建立网流规划模型,基于初始闭环潮流进行容量约束详细校验,并对没有通过校验的故障状态采用计算量较小的消圈法进行切负荷优化。

1 算法总体思路和流程

1.1 算法总体思路

高压配电网通常开环运行,特殊情况下可闭环运行。基于文献[13]提出的可靠性评估算法,枚举一种故障状态,可能出现以下4种情况:情况1,没有负荷失电;情况2,有负荷失电,负荷没有转供通道;情况3,有负荷失电,负荷仅有一个转供通道;情况4,有负荷失电,负荷有多个转供通道。若出现情况3和情况4,计算可靠性指标时则需要考虑容量约束。

对于情况3,负荷仅有一个转供通道,功率分布不受基尔霍夫第二定律约束,因此网流法不会产生误差。对于情况4,当一个转供通道不能满足负荷的需求时,可能会投入多个转供通道进行转供,负荷转供后可能环网运行,功率分布可能要考虑受基尔霍夫第二定律约束,利用网流法得到的结果与实际有一定偏差,但采用合适的潮流控制策略(如变电站解列运行)可以减小对功率分布的影响。

影响高压配电网可靠性评估结果的因素众多,例如:元件可靠性参数、系统运行方式、调度操作流程和切负荷方式等。每一种因素都会对可靠性计算结果造成影响,实际中很难获取所有因素的准确信息,因此目前可靠性评估主要用于方案的比选,而没有刻意追求预测的可靠性指标与真实的可靠性指标的吻合程度。因此,在相同的假设条件下,对不同的方案进行可靠性评估,可以筛选出可靠性更高的方案,从而指导电网的规划和改造。

网流法得到的结果反映了元件故障后系统的剩余供电能力的极限,采用合适的潮流控制策略(如变电站解列运行)可以达到这个极限,利用这个结果可以对不同的规划设计方案进行比选。

1.2 算法策略及流程

1.2.1 分区缩小计算规模

若能将大规模电网转化为若干个相对独立的小规模电网分别处理,将显著减小总的计算工作量。基于高压配电网联络关系,可以将大规模电网转化为若干个相对独立的小规模分区电网:检查高压配电网元件的联络关系,将有联络的元件归入同一个分区,将没有联络的元件归入不同的分区。分区后的故障状态集合可表示为U={U1,U2,…,Un},其中Un表示分区n的故障状态集合。对分区i的故障状态集合有Ui=Ci+Di,其中Ci表示分区i不需要切负荷的故障状态集合,Di表示分区i需要切负荷的故障状态集合。

1.2.2 初始闭环潮流计算

初始闭环潮流是指将所有联络开关闭合时计算得到的潮流。由于开环状态下有部分元件处于备用状态,将联络开关闭合计算闭环潮流可以使潮流分布更加均匀,元件的容量冗余更多,可简单识别更多满足容量约束的故障状态,进一步减少需要进行容量约束详细校验和切负荷的故障状态。

1.2.3 电压约束转化为容量约束

基于线路允许的最大电压损耗计算电压约束对应容量,与线路电流约束对应容量对比,选择两者较小值作为容量约束,将电压约束转化为容量约束。

1.2.4 容量约束保守校验

基于初始闭环潮流,某分区最小冗余容量是该分区各元件冗余容量中的最小值,是该分区剩余供电能力较为保守的上界,实际的剩余供电能力可能比这个上界要高。对于分区i,若在某种故障状态下失电负荷需要转供,若转供负荷小于该分区的最小冗余容量,则表示通过校验,将该故障状态归入集合Ci,否则归入集合Di。保守容量约束校验无需进行网络搜索,计算效率高。

1.2.5 容量约束详细校验

容量约束保守校验后得到的故障状态集合Di中可能仍有部分故障状态不需要切负荷,因此需要对集合Di中的故障状态进行详细校验。本文建立网流规划模型,利用改进的Edmonds-Karp方法[14]求解分区系统剩余供电能力。若某故障状态待转供的负荷不大于剩余供电能力,则表示容量详细校验通过,将该故障状态从集合Di中删除,同时加入集合Ci。

1.2.6 切负荷优化

对于分区i集合Di中的故障状态进行切负荷优化。考虑负荷重要程度的切负荷最小作为优化目标,将原问题转化为最小费用最大流问题,采用消圈法求解。

1.2.7 负荷点可靠性指标计算

考虑容量约束时,某故障状态i对应受影响负荷点的负荷将分为两部分:不能转供的负荷将感受故障修复时间,能转供的负荷将感受负荷转供时间。假设同一时段内负荷不变,节点n在时段j的停电时间可表示为:

(1)

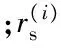
(2)

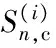
因此,考虑多时段的节点停电时间可表示为:

(3)

式中:T为划分的时段数量。

1.2.8 总体流程

对任意分区进行考虑容量约束的可靠性评估流程如附录A图A1所示。

2 基于电流和电压的容量约束

2.1 计算公式

基于电流的容量约束即传统容量约束,指线路通过的视在功率不应大于线路允许电流对应的容量,该容量可表示为:

(4)

基于电压的容量约束是指线路通过视在功率不大于允许最大电压损耗对应的容量。线路ij允许的最大电压损耗ΔUij,max可近似表示为[15]:

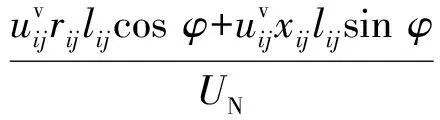
(5)

式中：rij和xij分别为线路ij单位长度电阻和电抗;lij为线路ij的长度;φ为电压电流相角差。

(6)

因此,线路ij基于电流和电压的容量可表示为:

(7)

2.2 分别基于电压和电流的容量比较

选取国内高压配电网常见的导线型号进行比较分析。假设功率因数为0.9,根据相关导则,非正常情况下高压配电网最大电压偏差不超过±10%[16],即理想情况下最大电压损耗不超过20%。110 kV和35 kV导线分别基于电流和电压的容量如附录A表A1所示。由表A1分析可知,若线路允许电压损耗为10%,线路长度小于30 km的110 kV城市高压配电网一般可忽略电压约束,但线路较长的110 kV高压配电网需要考虑电压约束的影响。线路长度小于10 km的35 kV城市高压配电网一般可忽略电压约束,但线路较长的35 kV线路需要考虑电压约束的影响。

3 切负荷最小网流规划模型

3.1 网流模型基础

3.1.1 费用流网络

费用流网络G=(N,A)是一个有向图,N表示节点集合,A表示边集合。图中每条边(i,j)∈A有非负的容量限制uij>0,边上通过非负的流量为xij,通过单位流量产生的费用为cij。流网络中有两个特殊的节点,即源节点s和汇节点t。

电网功率流是一个无向图,可在节点间采用方向相反的两条有向边将其转化为有向图。如附录A图A2所示,两节点边上流量均不小于0且任意时刻至少有一条边流量为0,且有cij=cji和uij=uji。

3.1.2 残留网络

残留网络Gf是由原始网络G中那些仍有空间对流量进行调整的边构成,残留网络用于表征原始网络各边的容量冗余。对任意流量不为0的有向边(i,j),该边的残留容量rij=uij-xij;相应反向边的残留容量rji=uji+xij。若两相连节点i,j∈N间没有流量通过,节点间两边残留容量为相应边容量,即rij=rji=uij。

3.2 切负荷最小模型

3.2.1 网络模型

网络模型如图1所示,它是一个简单的功率流网络模型。其中,节点0是电源点,节点1和2是连接点,节点3和4是负荷点;变量bi表示节点i的功率提供量或需求量,若bi<0表示节点i为电源点,若bi=0表示节点i为连接点,若bi>0表示节点i为负荷点。

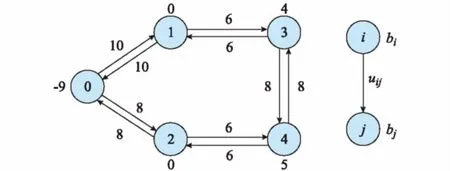
图1 功率流网络模型示意图Fig.1 Schematic diagram of power flow network model

3.2.2 优化模型

当有元件发生故障时,受元件容量的限制,某些负荷点可能需要进行负荷削减,本文考虑负荷重要程度的切负荷最小线性规划模型如式(8)至式(13)所示。其中,式(10)表示连接点功率平衡,式(11)表示电源点流出的功率不小于0,式(12)表示切负荷约束,式(13)表示元件容量约束。

目标函数:

(8)

约束条件:

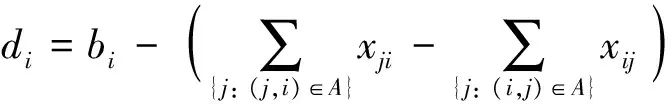
(9)

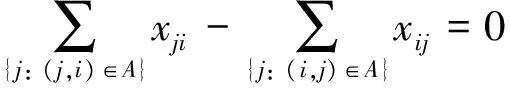
(10)

(11)

0≤di≤bi∀i∈Nd

(12)

0≤xij≤uij∀(i,j)∈A

(13)

式中:ci为节点i的重要程度(数值范围为1～10,数值越大越重要);di为节点i需要切掉的负荷;Ns为电源点的节点集合;Nc为连接点的节点集合;Nd为负荷点的节点集合(流网络中的节点分为电源点、连接点和负荷点3类)。

3.3 切负荷最小模型转换

3.3.1 网络模型转换

求解如式(8)至式(13)所示的线性规划原模型可采用传统的单纯形算法,但若采用最大流或最小费用流模型可以找到更高效的求解方法。原模型与最小费用最大流模型相似,但是与标准的最小费用最大流模型仍有差异:一是原模型负荷节点有流量需求;二是原模型边上没有费用。因此,需要事先对原模型进行一系列处理,转化成最小费用最大流模型。

首先,消去负荷点的流量需求。具体方法是为每个负荷点都添加一条虚拟边连接虚拟汇节点,然后将每条添加的边容量设置为对应负荷点的需求,将原负荷点的需求设置为0,这样所有负荷点均没有流量需求。然后,将每个负荷点的重要程度取反作为该负荷点对应虚拟边的费用。需要说明的是,转化后的网络模型仅虚拟边上有费用,其余边上费用为0,转化后的虚拟边反向边的容量为0。以图1的网络模型转化为例,结果如图2所示。

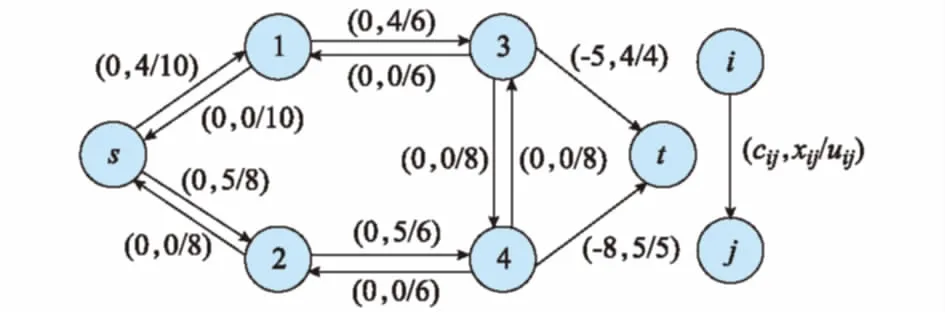
图2 转化后的功率流网络模型示意图Fig.2 Schematic diagram of transformed power flow network model

3.3.2 优化模型转换

转换后优化模型为:满足网络容量约束且流入汇节点的流量最大的条件下,使各边上消耗的费用最小,如式(13)至式(16)所示。其中,式(14)表示流过网络的费用最小,式(15)为最大流约束。

目标函数:

(14)

约束条件:

(15)

(16)

元件容量约束式(13)

式中:xmax为网络流入汇节点的最大流。

4 模型求解

4.1 求解思路

分析最小费用最大流模型(式(13)至式(16))不难发现,该模型包含了两个子问题:最大流问题和最小费用流问题。本文求解思路分为两步。

步骤1:求最大流或容量约束详细校验。在最大流条件下,若与汇节点相连的虚拟边均满流,则通过容量约束详细校验,不需要切负荷,此时费用也最小,否则需要进行步骤2的切负荷优化计算。

步骤2:求最小费用或确定切负荷的优化方案。在最大流的条件下,若虚拟边未满流,则需要在最大流的基础上进行流量调整,当总费用最小时可得到最优的切负荷方案。

4.2 最大流和容量约束详细校验

最大流结果可用以进行容量约束详细校验。本文最大流利用Edmonds-Karp算法求解[14],标准Edmonds-Karp算法思路如下:设网络流的初始值为0,在残留网络不断寻找源节点和汇节点间边数量最少的增广路径并对该路径进行增流,直到残留网络中不含增广路径则可求得网络的最大流。

为减少寻找增广路径的次数,本文对Edmonds-Karp算法进行了改进,即假设网络初始流量为系统初始闭环潮流。

4.3 切负荷优化算法

若容量约束详细校验未通过,则需要切负荷。在上述最大流的基础上求解最小费用,可以得到切负荷优化方案。

本文利用消圈法(cycle-canceling algorithm,CCA)求解最大流条件下的最小费用流[17]。设网络初始状态为最大流,在残留网络中不断寻找费用和为负的圈(只需要在负荷节点和汇节点间寻找,因为其他边费用均为0),然后对费用为负的圈进行增流,直到网络中不含有费用和为负的圈,此时流量分布为最小费用最大流。

5 算例分析

5.1 算例1:高压配电网分区和保守容量约束校验效果

某地区城市高压配电网有7座220 kV变电站,26座110 kV变电站,共72条110 kV线路。其中线路均满足“N-1”校验,22座110 kV变电站满足“N-1”校验。变电站根据110 kV变电站联络情况将高压配电网分为21个分区,每个分区仅有1～3个110 kV变电站。考虑到二阶故障,共1 131种故障状态下有负荷需要转供,其中未通过保守容量约束校验的故障状态为240种,未通过容量约束详细校验的故障状态为213种。因此,需要进行容量约束详细校验的故障状态数量占原故障状态数量的21.22%,需要进行切负荷优化的故障状态数量仅占原故障状态数量的18.83%,显著减少了计算量。

在所有故障状态中,会出现情况1(没有负荷失电)的故障状态占比为0%,会出现情况2(失电负荷无转供通道)的故障状态占比为36.25%,会出现情况3(失电负荷仅有一个转供通道)的故障状态占比为47.33%,会出现情况4(失电负荷有多个转供通道)的故障状态占比为16.42%。当出现情况4且转供后系统环网运行,分别基于网流法和直流潮流考虑容量约束需要切负荷时,可靠性评估结果可能不一致,这是由于网流法忽略了基尔霍夫第二定律可能产生的误差。对于具有弱环特点的高压配电网,出现这种情况的故障状态数量很少,由此导致的误差一般也不大。例如,对于本算例,仅有3种故障状态属于该情况(占故障状态总数的0.3%),而且对于这3种故障状态所在分区进一步分析,基于潮流计算考虑容量约束的系统平均停电时间(SAIDI)指标为0.065 43 h/(户·a),利用网流法考虑容量约束的SAIDI指标为0.065 28 h/(户·a),误差仅为0.23%,对于全系统的SAIDI,误差将进一步减小。

为了较为直观地说明引起误差的情况,以上述3种故障中的一种情况为例,故障前后的局部网络运行方式如附录A图A3所示。图A3(a)为正常运行,当线路1故障时负荷通过线路2转供,线路2不能转供全部负荷,母线联络开关闭合,与上级电网形成闭环运行方式,如图A3(b)所示。此时,利用网流法求解可以通过容量约束校验,潮流计算由于不能通过容量约束校验需要切负荷,从而导致可靠性指标出现误差。

5.2 算例2:采用消圈法进行切负荷优化

附录A图A4所示为RBTS-BUS4高压配电网部分[18],该配电网由3个变电站环形接线构成,正常情况下闭环运行。计算可靠性指标时需要枚举其故障状态,校验系统是否需要切负荷,若需切负荷则对切负荷进行优化。

原始算例仅有负荷参数,未提供运行参数、导线和变压器参数。假设功率因数为0.9,变压器容量均为12 MVA,L12导线型号为LGJ-95,L13和L23导线型号为LGJ-120,各条线路允许最大电压损耗为10%。采用原始算例中的峰值负荷,设置每天3个时段,各个时段的负荷系数分别为1,0.8和0.6。

本文切负荷优化的目标为考虑负荷重要程度的切负荷最小,因此还需要定义各个负荷点的重要程度,如附录A表A2所示。根据表A2的基础数据,对未通过容量约束校验的故障状态进行切负荷优化。计算结果表明,仅部分故障状态需要进行切负荷,切负荷优化结果如表1所示。

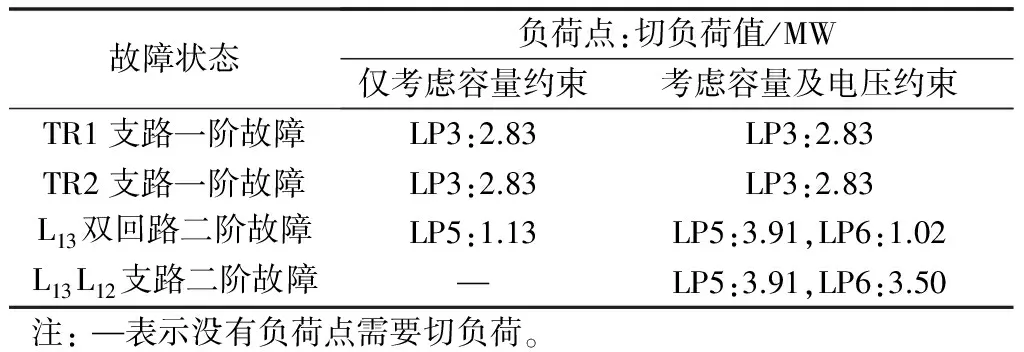
表1 切负荷优化结果Table 1 Results of load-cutting optimization

由表1分析可知,切负荷方案是在保证系统最大供电能力情况下优先切掉重要程度最低的负荷。“L13双回路二阶故障”和“L13L12支路二阶故障”考虑容量及电压约束的切负荷量大于仅考虑容量约束的切负荷量。

考虑了元件容量和电压约束,高压配电网可靠性评估更加符合实际情况,RBTS-BUS4可靠性评估指标如表2所示。

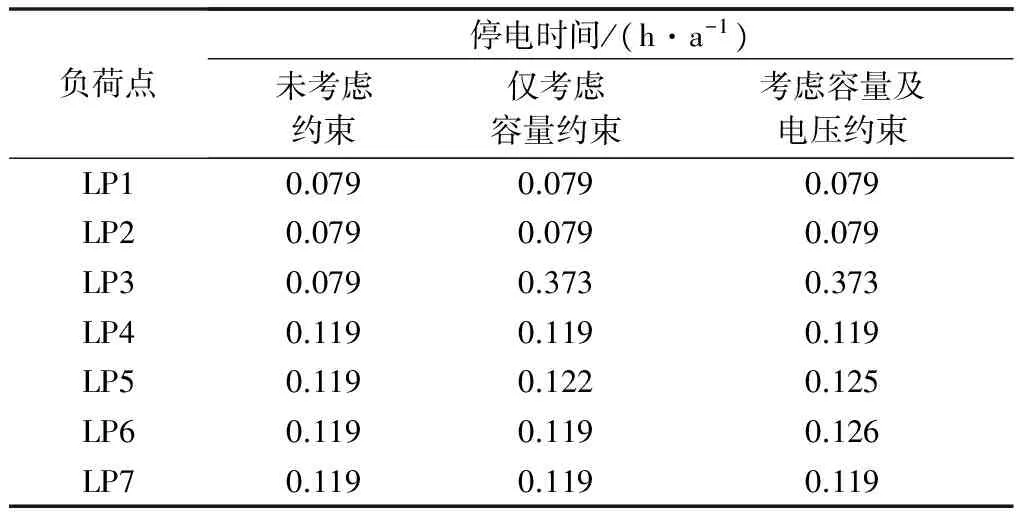
表2 负荷点停电时间指标对比Table 2 Comparison of outage time index for load points

由表2可见,由于考虑容量约束,负荷点LP3,LP5和LP6的停电时间大于未考虑约束情况下对应的负荷点停电时间。同时由于算例为33 kV且线路较长,电压约束起到了较大的作用,因此当同时考虑容量和电压约束时,LP5和LP6的停电时间进一步增大。

为验证算法的有效性,本文设计了3组方案对算例计算时间进行对比。方案1表示未进行容量约束校验,直接利用消圈法进行切负荷优化;方案2表示容量约束保守校验后,利用消圈法进行切负荷优化;方案3表示容量约束保守和详细校验后,利用消圈法进行切负荷优化。图3所示为各个方案的计算时间。

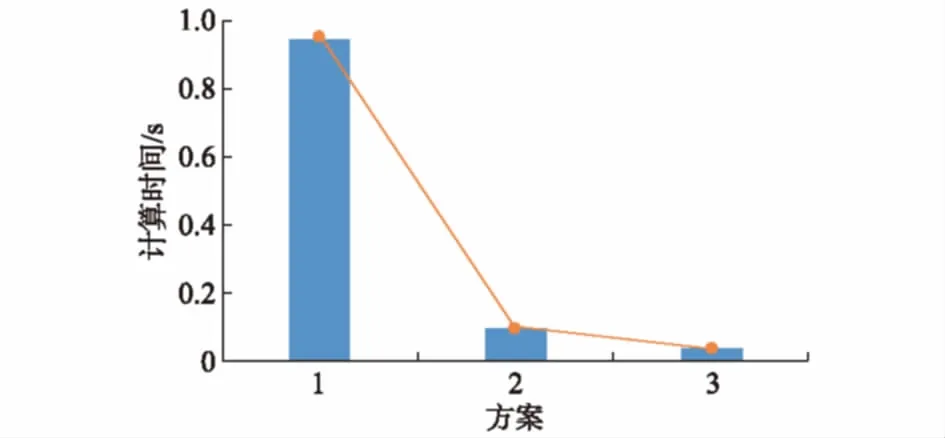
图3 各方案计算时间对比Fig.3 Comparison of computation time for different approaches

由图3分析可知,容量约束保守和详细校验均可减少计算时间,其中容量约束保守校验计算时间减少量最为明显。

6 结语

基于高压配电网的特点,提出了一种完整的考虑容量和电压约束的高压配电网可靠性快速评估算法,得到结论如下。

1)根据高压配电网各接线方式相对独立的特点,对高压配电网进行分区,将大规模电网转化为多个小规模电网,显著减少网络计算搜索范围。

2)基于估计的各线路允许最大电压损耗将其转化为相应容量约束,考虑容量约束时自动考虑了电压约束,简化了评估流程。

3)基于初始闭环潮流的元件负载率对故障状态进行保守容量约束校验,快速筛选出部分不需要进一步容量校验和切负荷的故障状态,无需网络搜索。

4)建立考虑容量约束的切负荷最小网流规划模型,基于初始闭环潮流利用改进的Edmonds-Karp算法做进一步容量约束校验。

5)算例计算分析表明:精度方面,与直流潮流相比网流法很少会产生误差,且误差小;速度方面,提出的方法显著减少了计算量,提高了计算效率。

同时,在以下几个方面进行了讨论。

1)为进一步提高计算精度,可考虑对局部相关网络采用基于直流潮流和单纯形算法的切负荷优化方法。对于存在负荷途经多段线路的各线路段最大允许电压损耗分配问题,本文仅利用负荷矩(即功率与线路长度的乘积)作为权重进行估算,将在后续的工作中做进一步的研究。

2)本文计算的可靠性指标为负荷点年平均停电时间,其余两个负荷点可靠性指标,即故障率和每次故障平均停电持续时间,也可以通过本文算法求得,系统可靠性指标则可由负荷点可靠性指标推导得到。

3)由于中压配电网可靠性评估也可能涉及多个方向负荷转供的问题,本文方法有望推广应用到该领域。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 配电网规划设计技术导则:Q/GDW 738—2012[S].北京:国家电网公司,2012.

[2] 城市电力网规划设计导则:Q/CSG 1 156—2006[S].北京:国家电网公司,2006.

[3] 赵渊,周家启.发输电组合系统可靠性评估的最优负荷削减模型研究[J].电网技术,2004,28(10):34-37.

ZHAO Yuan, ZHOU Jiaqi. Research of the optimal load shedding model in the composite generation and transmission system reliability evaluation[J]. Power System Technology, 2004, 28(10): 34-37.

[4] 张巍峰,车延博,刘阳升.电力系统可靠性评估中的改进拉丁超立方抽样方法[J].电力系统自动化,2015,39(4):52-57.DOI:10.7500/AEPS20140220002.

ZHANG Weifeng, CHE Yanbo, LIU Yangsheng. Improved Latin hypercube sampling method for reliability evaluation of power systems[J]. Automation of Electrical Power Systems, 2015, 39(4): 52-57. DOI: 10.7500/AEPS20140220002.

[5] PAPADIMITRIOU C H, STEIGLITZ K. Combinatorial optimization: algorithms and complexity[M]. North Billerica, USA: Courier Corporation, 1982.

[6] 吴素农,吴文传,张伯明.考虑传输容量约束的配电网可靠性快速评估[J].电网技术,2009,33(14):21-25.

WU Sunong, WU Wenchuan, ZHANG Boming. An efficient reliability evaluation method for distribution system with transmission capacity constraints[J]. Power System Technology, 2009, 33(14): 21-25.

[7] 赵洪山,王莹莹,陈松.需求响应对配电网供电可靠性的影响[J].电力系统自动化,2015,39(17):49-55.DOI:10.7500/AEPS20150205007.

ZHAO Hongshan, WANG Yingying, CHEN Song. Impact of demand response on distribution system reliability[J]. Automation of Electrical Power Systems, 2015, 39(17): 49-55. DOI: 10.7500/AEPS20150205007.

[8] 昝贵龙,赵华,吴延琳,等.考虑容量及电压约束的配电网可靠性评估前推故障扩散法[J].电力系统自动化,2017,41(7):61-67.DOI:10.7500/AEPS20160614009.

ZAN Guilong, ZHAO Hua, WU Yanlin, et al. Forward failure diffusion algorithm for reliability evaluation of distribution networks considering capacity and voltage constraints[J]. Automation of Electrical Power Systems, 2017, 41(7): 61-67. DOI: 10.7500/AEPS20160614009.

[9] 王主丁,韦婷婷,万凌云,等.计及多类开关和容量约束的中压配电网可靠性估算解析模型[J].电力系统自动化,2016,40(17):146-155.DOI:10.7500/AEPS20151231002.

WANG Zhuding, WEI Tingting, WAN Lingyun, et al. Analysis reliability estimation model of medium voltage distribution networks considering different types of switches and capacity constraints[J]. Automation of Electrical Power Systems, 2016, 40(17): 146-155. DOI: 10.7500/AEPS20151231002.

[10] 邵黎,谢开贵,王进,等.基于潮流估计和分块负荷削减的配电网可靠性评估算法[J].电网技术,2008,32(24):33-38.

SHAO Li, XIE Kaigui, WANG Jin, et al. Reliability evaluation algorithm of distribution network based on power flow estimation and section load shedding[J]. Power System Technology, 2008, 32(24): 33-38.

[11] 赵渊,周家启,谢开贵.基于网流规划的发输电组合系统可靠性评估模型研究[J].电网技术,2003,27(10):21-24.

ZHAO Yuan, ZHOU Jiaqi, XIE Kaigui. Study on reliability assessment model of composite generation and transmission system based on network flow programing[J]. Power System Technology, 2003, 27(10): 21-24.

[12] 王锡凡.电网可靠性评估的随机网流模型[J].电力系统自动化,2006,30(12):1-6.

WANG Xifan. Probabilistic network-flow models for reliability evaluation of power networks[J]. Automation of Electric Power Systems, 2006, 30(12): 1-6.

[13] WANG Zhuding, FARROKH S, QIU Jun. An efficient algorithm for assessing reliability indexes of general distribution systems[J]. IEEE Trans on Power Systems, 2002, 17(3): 608-614.

[14] CORMEN T H, LEISERSON C E, RIVEST R L.算法导论[M].北京:机械工业出版社,2006.

[15] 陈慈萱.电气工程基础:上册[M].2版.北京:中国电力出版社,2012.

[16] 电力工业部.供电营业规则[M].北京:中国电力出版社,2001.

[17] AHUJA R K, MAGNANTI T L, ORLIN J B. Network flows: theory, algorithms, and applications[M]. Upper Saddle River, NJ, USA: Prentice-Hall Inc, 1993.

[18] ALLAN R N, BILLINTON R, SJARIEF I, et al. A reliability test system for educational purposes: basic distribution system data and results[J]. IEEE Trans on Power Systems, 1991, 6(2): 813-820.

Efficient Reliability Evaluation Algorithms for High Voltage Distribution Network Considering Capacity and Voltage Constraints

ZANGuilong1,WANGZhuding1,LIUNianzu2,WUYanlin3,WANGXiaobo2,WANGGuoliang2

(1. State Key Laboratory of Power Transmission Equipment & System Security and New Technology (Chongqing University), Chongqing 400044, China; 2. State Grid Zhengzhou Power Supply Company, Zhengzhou 450000, China; 3. Economic and Technological Research Institute of State Grid Shaanxi Electric Power Company, Xi’an 710000, China)

As few studies on reliability evaluation of high voltage distribution networks are available, a new hybrid algorithm is proposed to consider capacity and voltage constraints for the reliability evaluation of a high voltage distribution network. Based on the weakly-meshed feature of a high voltage distribution network, a large-scale grid is partitioned into multiple small-scale grids. A voltage constraint is transformed into its corresponding capacity constraint so that the subsequent voltage constraint is no longer considered. It is proposed that a capacity constraint be conservatively checked based on the elements capacity redundancy with all tie-connections being closed. Thus partial fault states that are not restrained by capacity are rapidly screened out. The network flow method is employed for the reliability evaluation of high voltage distribution networks and detailed capacity constraint checking is conducted using the maximum flow capacity model. Finally, the cycle-canceling algorithm is employed to efficiently obtain the minimum load-cutting. The numerical results show that the execution time is significantly shortened by the high voltage distribution network partition in addition to conservative and detailed capacity constraint checking when the requirement of engineering calculation accuracy is satisfied.

high voltage distribution network; reliability evaluation; voltage constraint; capacity constraint; network flow method; minimum load-cutting

2016-12-26;

2017-04-16。

上网日期: 2017-06-14。

昝贵龙(1992—),男,通信作者,硕士研究生,主要研究方向:电力系统规划、运行与可靠性。E-mail：zan_gl@163.com

王主丁(1964—),男,教授,IEEE高级会员,主要研究方向:电力系统规划、运行与可靠性。E-mail: 348402467@qq.com

刘念祖(1986—),男,工程师,主要研究方向:电网规划设计。

(编辑 章黎)