分布式制造供应链低碳集货模型与算法研究

史雨同，尹 静，王柏琳

（1.北京建筑大学 机电与车辆工程学院，北京 100044；2.北京科技大学 东凌经济管理学院，北京 100083）

分布式制造供应链低碳集货模型与算法研究

史雨同1，尹 静1，王柏琳2

（1.北京建筑大学 机电与车辆工程学院，北京 100044；2.北京科技大学 东凌经济管理学院，北京 100083）

针对我国当前严峻的环境形势和节能减排的现实要求，研究了低碳环境下分布式制造供应链节点集货问题，研究过程中应用了最小碳排放和最短路径的多目标优化模型。算法上设计了三阶段集成启发式方法分步求解，首先采用遗传算法找到最短路径的集货方案；在此基础上采用节约算法的基本思想进行路径拆分和车辆匹配，降低碳排放水平；最后通过计算碳排放节约值对集货方案进行局部重组，进一步优化碳排放指标。仿真实验表明，分阶段的求解方法可以设计出碳排放更优的解，同时满足经济效益和环境效益。

制造供应链；碳排放；集货模型；路径优化

1 引言

随着网络时代的到来，以往所有零部件自有生产模式已经无法经受市场的考验，很多制造企业特别是汽车公司趋向于采用分布式制造模式。由于生产不同零件的厂商分散在不同的地理区域，导致集货过程中物流成本上升和碳排放问题日益突出，减少集货过程中的成本和碳排放，成为我国当前经济发展的重要课题。

运输成本和距离是之前集货问题研究的主要目标，因此大多数学者将集货问题归于车辆路径问题（Vehicle Routing Problem VRP）进行研究。前期的研究主要集中于无时间窗要求的VRP问题，潘震东等[1]研究了带货物权重的VRP问题，马天宇等[2]用遗传算法研究了分区的多配送中心车辆调度问题。随着JIT思想在制造行业中普及，对配送时间的要求越来越高，产生了带时间窗的车辆路径问题（Vehicle Routing Problem with Times Windows,VRPTW)。Ziauddin U等[3]设计出局部优化框架，并结合遗传算法解决了带时间窗的车辆路径问题。Tan K C等[4]采用启发式与合并式相结合的交叉算子，融入了爬山算法和自适应变异机制，设计出了改进遗传算法解决VRPTW问题。

2009年哥本哈根全球气候峰会以来，我国对环境的重视程度越来越高，碳排放成为我国环境保护的重要指标。减少集货过程中的碳排放量成为国内学者与企业管理人员关注的焦点。目前以减少碳排放为目标的集货问题研究还比较少，邱雅君等通过改进遗传算法求解了考虑碳排放因素的VRP问题[5-6]。Kirby认为车辆碳排放与燃油消耗成正比，可以将碳排放量和油耗问题一起研究[7]。史春阳[8]在给出了公路运输中二氧化碳排放的计算方法后，针对同时取送货的车辆路径问题（VRPSPD）进行了低碳研究。

本文以最小碳排放和最短距离为目标建立多目标优化模型。碳排放的计算基于油耗，运输过程需满足时间窗和载重等多重约束，并考虑车型多样和车辆数有限的情况。本文在算法设计方面采用了基于遗传算法和启发式节约算法的分阶段法，分步求解最短路径和最小碳排放问题，结果表明，该算法可用于解决低碳车辆路径问题，找到低碳的集货方案。

2 问题描述和数学模型

2.1 问题描述

本文研究问题可描述为：配送中心派遣一组车辆前往供货商处取货，然后返回配送中心。供货商的地理位置、供货数量、供货时间窗和装货时间已知；配送中心保有多种类型的车辆且每种车型数量已知；车辆行驶过程看作匀速过程。目标是在满足各种约束的前提下，找到总路径最短和碳排放量最小的车辆选择和路径安排。集货过程中的约束如下：

（1）配送中心约束：所有车辆由配送中心驶出，完成取货任务后返回配送中心；

（2）车辆约束：配送中心有多车型的货车，每种车型的数量和参数已知；

（3）访问唯一性约束：每个供货商只能被一辆车一次性服务；

（4）载重约束：每种类型车辆的装载量需满足该车型的容量限制；

（5）时间窗约束：供货商只能在规定的时间窗内被车辆服务，如果车辆到达的时间早于最早开始服务时间，车辆将在供货商处等待，如果车辆在最晚开始服务时间之后到达，则产生不可行解；

（6）装货时间约束：车辆到达供货商后需完成装货过程，装货时间固定且已知；

（7）速度约束：行驶过程中所有车辆以相同的速度匀速行驶。

2.2 符号和决策变量

G=(V,E)：物流配送网络；

V：供货商集合，V={0,1,2,…,n},其中0表示配送中心，其他数表示供货商；

E：弧集，E={(i,j)|i,j∈V,i≠j}；

P：表示一条从配送中心出发，完成服务过程又回到配送中心的路径；

Pi,j,…：表示包含供货商i,j,…的路径，i,j,…∈V；

Dij：弧（i,j）的距离；

Rij：车辆行驶Dij所用的时间；

Si：供货商i开始服务的时间；

Ti：供货商i的装货时间；

[ETi,LTi]：供货商i的时间窗，其中ETi为最早开始服务时间，LTi为最晚开始服务时间；

k：表示车辆集合，k={1,2,…,kK}；

Qijk：车辆k从i发往j的过程中的载重；

m：表示车型集合，m={1,2,…,mM}；

Nx：x车型的数量；

Qx：x车型的容量；

Ui：供货商i的供货量。

UP：路径P的集货量，UP=∑Ui，i为路径P上的供货商。

决策变量定义为：

2.3 碳排放计算

本文根据实际问题的需要，采用文献[8]中史春阳等的计算方法，忽略了速度和道路坡度的影响，采用了以排放系数、行驶距离和装载量为基础的油耗计算方法：

然后由油耗来计算碳排放量：

本文碳排放的数学模型采用三下标模型（threeindex model），前两个下角标表示两端的供应商，第三个角标表示选择的车辆[9]，如下：

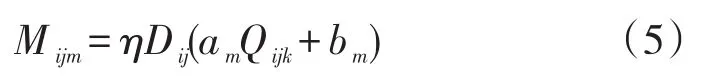
其中，F为燃油消耗；D为行驶距离；Q为车辆当前载重；a,b为燃油排放系数；M为碳排放量；η为燃油转换系数；Mijm为m类型的车从供货商i到j的碳排放量；Dij为i到j的距离；am和bm为m类型车的燃油消耗系数；Qijk为车辆k在i和j运输过程中的载重。

从式（3）-式（5）可知，碳排放和车辆排放系数相关，和行驶距离成正比，和负载量成正线性相关。

2.4 多目标优化模型

本文研究的最短路径和最小碳排放集货问题可表示如下：

式（6）表示运输过程中总路径最短；式（7）表示运输过程中碳排放量最小；式（8）表示载重限制；式（9）表示一个供应商能且只能被一辆车服务，并且只能被访问一次；式（10）-（12）表示所有由k车集货的点构成一条Hamilton回路；式（13）表示车辆数为所有类型车辆的总和；式（14）、（15）表示配送中心限制；式（16）表示时间窗限制；式（17）表示决策变量的取值范围。

3 算法设计

由于本文研究的集货问题属于NP-hard问题，不能直接计算出最优解。本文采用遗传算法和启发式算法相结合的分阶段法寻找最小碳排放的集货策略。算法阶段1在多约束前提下用遗传算法求解最短路径问题。算法阶段2对阶段1中结果中的每条路径进行路径拆分和车辆匹配，结合不同车型数量的约束选择碳排放最小的路径拆分方法。阶段3完成路径局部重组，将负载率较低的路径作为优化目标，通过合并其他供货商节点的方式进一步降低集货过程中的碳排放量。

任意路径上的车型选择原则为：在车型集合m中，选择车辆容量Qx≥UP且最接近UP的车型作为集货车辆，不考虑车辆数量的限制。

3.1 最短路径遗传算法

阶段1首先不考虑碳排放的因素，将集货问题转换为带时间窗、最大载货量和车辆数限制的VRP问题，并采用遗传算法进行求解，计算过程如下：

（1）编码生成。本文采用自然数编码，每个染色体S代表一个路径解，即一种路径规划方案。它由若干条子路径的集合组成，S={P1,P2,…,Pn}。每条

子路径为若干供货商节点的集合，P…i,j,…={…i,j…}，由一辆车按照先后顺序装载集货。（2）生成初始种群。按照编码生成方式生成路径解，根据约束检查判断是否为可行解。最终生成一组数量为NC的染色体种群作为初始种群。

时间约束检查：

对于E路径P中的两个相邻节点i和 j（i在 j之前），如果ETi+Ti+Rij≤LTj，则满足时间窗约束，否则不满足。

载重约束检查：

对于可用车型1，2，…，mM，车型数量分别为N1,N2,…,NmM，载重量分别为 Q1,Q2,…,QmM，有Q＜Q2＜…＜QmM。 如 果 UP＜Q1 的 个 数，则满足载重约束，否则不满足。

（3）适应度的计算。本文的适应值函数fh=1/Z，fh是种群中个体生存能力的表现，fh越大表明其性能越好，即其对应的解越接近最优解。

（4）选择。将每一代产生的染色体按适应度值从小到大排列。第一个染色体直接进入下一代，剩下的染色体则通过轮盘赌的方式进行选择，最终有NC个个体进入下一代。一个个体被选择的概率为：

这里，f(xi)为个体xi的适应度，F(xi)为个体被选择的概率[10]。

（5）交叉。选择[Nc/2]对染色体进行随机配对，交叉概率为PC，具体操作为：产生一个（0，1）内的随机数r，如果r≤PC，则将配对的染色体进行交叉。本文采用连续正向交叉的方式。

（6）变异。按变异概率Pm对染色体进行变异操作，具体操作方式为：产生一个随机数r，若r≤Pm，则进行变异操作。变异算子为对换变异。

（7）停止。当算法迭代代数达到Nn时，停止进化，输出适应度最大的染色体对应的路径作为最优解。

本算法输出结果为一组路径{P1,P2,…,Pn}，根据每条路径的集货量依据车型选择原则选择车型，确定集货方案。

3.2 路径拆分与车辆匹配

通过上述遗传算法可以解决最短路径问题，本文算法阶段2采用节约算法的基本思想对每一条路径进行拆分和车辆匹配，寻找碳排放更少的集货方案。具体计算步骤如下：

首先定义碳排放节约值：

Mpi表示路径Pi的碳排放。

某条拥有n个供货商的路径的拆分步骤如下：

Step 1：让各个供货商单独送货，形成初始路径P1,P2,…,Pn。

Step 2：令k=2，3，...，n，依次执行以下步骤：

（1）计算任意k个路径Pi,Pj,…,Pk的节约值s(Pi,Pj,…,Pk)，并将其定义为数组。

（2）若s(Pi,Pj,…,Pk)的值均 ≤0，则转入Step 2（4）；否则在节约值s(Pi,Pj,…,Pk)内求出值为最大的那一 项s(…Pi,Pj,…)，将路径 …Pi,Pj,… 合并为P…i,j,…，转入Step 2（3）。

（3）计算新路径下的节约值s(Pi,Pj,…,Pk)，转入Step 2（4）。

（4）记录下当前的路径安排和车辆选择，计算当前碳排放Mk。

Step 3：比 较M2、M3、…Mn的 值 ：若∀k∈[ ]

2,n-1，有Mk≤Mn，说明该路径上的路径拆分不能减少碳排放，则路径不予拆分，算法结束；否则转Step4进行路径拆分。

Step4：计算Mk-Mn（∀k∈[ ]2,n-1），取其中的最大正数作为碳排放节约值，并记录相应的路径拆分车型选择。

通过以上路径拆分方法可以输出一组数据{En.Pn,kn,Pn',kn'}，其中En为＞0的碳排放节约值；Pn为En在最短路径的遗传算法结果中对应的路径；kn为Pn占用车辆集合；Pn'为En对应的拆分后的路径；kn'为Pn'占用车辆集合。记所有车辆的集合为k，最短路径的遗传算法结果中占用车辆集合为k0，车型可用集合初始值k*为（k-k0），车辆匹配步骤如下：

Step 1：将路径拆分后得到的En定义为数组，在所有路径Pn中设置选择参数“已拆分/未拆分”，并将初始状态设置为“未拆分”。

Step 2：如果所有En都≤0，则结束该算法；如果有En＞0，找到En中的最大量E1和路径拆分方法结果中E1对应的P1,k1,P1',k1'，将E1定义为0，转入Step 3。

Step 3：如果路径P1选择参数为“已拆分”，则转入Step 3；否则转入Step 4。

Step 4：如果 (k-k0+k1-k1*)中所有车型数都≥0，则按该拆分方法进行路径拆分和车辆匹配，将P1定义为该拆分方法进行路径拆分和k*更新为（k*+k1-k1

*），转入Step 2，否则直接转入Step 2。本算法在不同车型数量的约束条件下寻找碳排放最优的路径拆分和车辆匹配方法，生成新的集货方案。由于最短路径遗传算法中的解是在硬时间窗的约束条件下求得的，拆分后的路径和车辆选择仍满足时间窗的要求。

3.3 路径局部重组

通过路径的拆分可以找到碳排放更少的集货方案，但路径拆分只能在阶段1最短路径的基础上寻求每条路径上的碳排放最小集货方法，而没有考虑路径间的重组。本文算法第3阶段对只有一个供货商的路径与其他路径进行局部重组，寻找碳排放更少的集货方法。

局部重组的基本思想是：让由一辆车单独服务的供货商与其他供货商组成新的路径，参与重组供货商从原路径拆分出后也形成一条新的路径，计算重组前后的碳排放节约值，寻找碳排放更低的集货方案。通过时间窗的约束和局部重组前后碳排放的对比验证局部重组的可行性。

对于只有一个供货商i的路径Pi，路径重组的步骤如下：

Step 1：对于路径拆分和车辆匹配算法输出的路径组合，将供货商j(j∈n且j≠0,j≠i)从原路径Pj中拆分出来，与i组成新路径Pi,j，Pj中剩余供货商组成新路径Pj'，计算碳排放节约值s(i,j)。碳排放节约值的计算方法为：s(i,j)=WPi+WPj-WPi,j-WPj'。

Step 2：对供货商i和j进行时间约束检查。如果满足时间约束，则转入Step 3，否则令s(i,j)=0，转入Step 3。

时间约束检查：

如果供应商i和j同时满足ETi+Ti+Rij＞LTj;ETj+Tj+Rij＞LTi，则i和j不满足时间约束；否则满足。

Step 3：对供货商i和j进行车型数量约束检查。如果满足车型数量约束，则转入Step 4；否则令s(i,j)=0，转入Step 4。

车型数量约束检查：

所有车辆的集合为k，拆分集货方法已用车辆集合为k0，路径Pj和Pi所用车辆集合为k1，路径Pi,j和Pj'所用车辆集合为k2，如果集合（k-k0+k1-k2）中所有车型数都≥0，则满足车型数量约束，否则不满足约束。

Step 4：找出碳排放节约值最大值Max s(i,j)，记录相应的路径重组和车型匹配方法。

对所有由一辆车单独集货的供货商执行以上操作，在车型数量约束条件下寻找最优的路径重组策略。

4 算例分析

4.1 参数设置

本文算例与数据来源于国内某大型物流企业A为华晨宝马汽车装配线B供货的实际问题。B在上海市附近有50家供货商，供货商的位置已知，每天有不同的供货商按照生产计划需求给总装厂供货，B与其供货商共同拟订供货时间窗和装货时间，供货厂家以及数量等信息会提前发送给A企业，然后由A企业分派车辆完成集货任务，所有车辆从上海配送中心出发，遍历所有的供货商，完成集货过程然后返回配送中心。

配送中心和供货商的地理位置已知，配送中心拥有的车辆类型和数量已知。某天共有15家供货商需要为A供货，具体数据见表1，位置如图1所示。

表1中序号0代表配送中心，1-15代表15家供货商。配送时间为8点至第二天6点。时间单位为0.1h，也就是6min。从8点开始计时，车辆要在220个时间单位也就是22h内完成集货并回到配送中心。长度单位为5km，文中忽略了速度对碳排放的影响，假设车辆以速度50km·h-1匀速行驶。配送中心共有3种类型10辆车可供使用，车辆的具体信息见表2。

表2 车辆信息

车辆的里程数不限，燃油转换率取2.610kg·L-1[11]。某类型车辆的每公里碳排放可根据排放标准A和排放标准B及燃油转换率η参考式（3）。

4.2 计算结果

（1）最短路径的遗传算法：种群规模Nc取50，交叉概率Pc设置为0.5，变异概率Pm设置为0.05，更迭代数Nn取1 000。每种目标函数下运行20次，路径最短集货方案见表3，路径如图2所示。

表3 阶段1集货方案

图2 阶段1的路径

（2）路径拆分与车辆匹配算法：分别对最短路径遗传算法产生的5条路径进行拆分，寻求碳排放最小的拆分方法。结果如下：（0-10-1-9-15-0）；（0-12-4-5-13-0）；（0-6-0）三条路径任何拆分方法都不能减少碳排放，不进行拆分。（0-2-11-3-0）在拆分为（0-2-11-0）和（0-3-0）时，碳排放节约值为8 130.15kg；根据已有车型数量限制和车型选择原则，路径拆分和车辆匹配后的集货方案见表4，路径如图3所示。

表4 阶段2集货方案

（3）路径局部重组算法：对路径拆分与车辆匹配算法产生的的单点路径进行局部重组，寻找碳排放更小的集货方法。重组后的集货方案见表5，路径如图4所示。

各阶段得到的集货方案行驶距离和碳排放指标数值见表6。

表1 配送中心和供货商信息

图3 阶段2的路径

表5 阶段3集货方案

图4 阶段3的路径

表6 运算结果

由表6可知，从阶段1的最短距离集货方案到阶段3的最小碳排放集货方案，距离仅增加了33km，碳排放降低了0.14t，在最短距离方案的基础上降低碳排放量，同时优化经济效益与环境效益，是切实可行的。

5 结语

低碳环境下分布式制造供应链集货问题的研究是我国现阶段面对的重要课题，对于推广“绿色物流”，完成节能减排目标有着重大意义。针对该问题，本文提出了基于油耗的碳排放计算方法，将路径优化和最小碳排放量结合起来，建立统一的多目标优化模型。为了降低计算复杂度，本文设计了分阶段算法进行求解。首先用遗传算法解决最短车辆路径问题，产生初始集货方案，进而基于节约算法的基本思想对所得方案中的路径进行拆分和重组，根据车型数量限制匹配车辆，得到更为低碳的集货方案。实例中拆分重组后的集货方案较之前降低了0.14t碳排放量，可以看到本文提出的模型和算法是有效的。

本文碳排放量应用了考虑车型、运载量和行驶距离的计算方法，没有考虑行驶速度和路况等因素的影响，未来可进一步深入探讨，同时可以考虑提取问题特征，将智能搜索与进化计算方法结合起来设计开发求解算法，提高计算效率，降低问题的计算复杂度。

[1]潘震东,唐加富,韩毅.带货物权重的车辆路径问题及遗传算法[J].管理科学学报,2007,10(3):23-29.

[2]马宇红,姚婷婷,张浩庆.基于分区的多配送中心多车型车辆调度问题与遗传算法设计[J].科技导报,2013,31(2):61-67.

[3]Ziauddin U,Daryl E.Localized genetic algorithm for vehicle routing problem with time windows[J].Applied Soft Computing,2011,11(8):537-539.

[4]Tan K C,Lee L H,Zhu Q L.Heuristic methods for vehicle routing problem with time windows[J].Artificial Intelligence in Engineering,2001,15(3):281-295.

[5]邱雅君,宋国防.考虑碳排放因素的车辆路径问题研究[J].物流技术,2012,(7):222-226.

[6]雷兆明,王东东,廖文喆,等.Levy人工蜂群在钢铁企业供应端的优化[J].科学技术与工程,2016,(28):251-258.

[7]Kirby H R,Hutton,Quaid R W.Modeling the effects of transport policy levers on fuel efficiency and national fuel consumption.Transport research part D[J].Transport and Environment,2000,5(3):265-282.

[8]史春阳,赵磊.同时取送货的车辆路径问题中的低碳研究[D].北京:清华大学,2011.

[9]Montane F,Galvao R D.A tabu search algorithm for the vehiclerouting problem with simultaneous pick-up and delivery service[J].Computers&Operations Research,2006,33:595-619.

[10]雷英杰,张善文.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2014.

[11]Ubeda S,Arcelus F J,Fanlin J.Green logistics at Eroski:A case study[J].International Journal of Production Economics,2011,131:44-51.

Study on Low-carbon Cargo Consolidation Model and Algorithm of Distributive Manufacturing Supply Chain

Shi Yutong1,Yin Jing1,Wang Bailin2
(1.School of Electrical&Mechanical Engineering,Beijing University of Civil Engineering&Architecture,Beijing 100044;2.Dongling School of Economics&Management,University of Science&Technology Beijing,Beijing 100083,China)

In this paper,in view of the several environment condition in China and the realistic demand of the initiative to cut energy consumption and emissions,we studied the issue of cargo consolidation of a distribution manufacturing supply chain within the low-carbon environment,during which the optimization model that intended to both minimize carbon emissions and distribution distance was used;the on such basis,we approached the route division and vehicle matchmaking following the fundamental principle of the saving algorithm so as to lower the carbon emissions level;and at the end,we regrouped partially the cargo consolidation solution in light of the calculation result to further optimize the carbon emissions index,the validity of which was demonstrated through a simulation study.

manufacturing supply chain;carbon emissions;cargo consolidation model;route optimization

F224.0;F274

A

1005-152X(2017)10-0114-07

10.3969/j.issn.1005-152X.2017.10.023

2017-09-04

北京市自然科学基金项目（9174038）；北京市教委科技计划面上项目（Z14012）；长城学者计划（CIT&TCD20150312）

史雨同（1992-），男，河南开封人，硕士生，主要研究方向：物流系统调度与仿真；尹静（1978-），女，通讯作者，河北石家庄人，副教授，博士，硕士生导师，主要研究方向：生产调度与物流优化；王柏琳（1983-），女，河北石家庄人，讲师，博士，主要研究方向：生产计划与调度。