第2讲 海冰动力学

刘煜，吴辉碇

（国家海洋环境预报中心，海洋灾害预报技术重点实验室，北京 100081）

第2讲 海冰动力学

刘煜，吴辉碇

（国家海洋环境预报中心，海洋灾害预报技术重点实验室，北京 100081）

简单回顾了海冰动力学的发展，介绍了海冰漂移、形变和堆积等动力学过程，对比分析了不同海冰本构关系在海冰流变学的应用。

海冰；动力学；流变学；本构关系

1 引言

影响海冰发生和发展的物理过程主要分为热力学、动力学两种过程。大气和海洋间的热量交换造成海水冻结和海冰形成。海冰厚度增长和消融的长期趋势主要依赖于大气、海洋和海冰间的能量交换，这些过程是构成海冰热力学模式的基础。在极地和区域海域，海冰漂移和形变主要依赖于动力过程，受其影响，海冰冰脊和水道的形成可以在短时间内明显改变海冰厚度及分布。海冰动力过程主要取决于气-冰-海间动量交换以及冰内应力，上述过程构成了海冰动力学模式的基础。

海冰运动主要受大尺度气-冰-海相互作用影响，是决定海冰分布和形变的主要因素。海冰动力学主要包括海洋、大气动力强迫下海冰的运动变化、动量传输、冰内相互作用以及海冰堆积、脊化、破碎、断裂等相关过程，主要分为以下3个方面：（1）海冰漂移的动量平衡；（2）决定海冰内应力和形变、冰强度关系的流变学；（3）由海冰分布所决定的海冰强度。海冰运动受到以下5种力作用：风应力、科氏力、冰内应力、海流应力和海面高度梯度力。海冰内应力的处理历来是计算海冰动力学模式的难点和关键。

早期海冰动力学研究主要探讨海冰自由漂移的规律，并不注重海冰之间相互作用的研究[1-3]。其后海冰流变学的复杂性逐渐成为动力学研究的重点，主要包括：将海冰作为线性粘性流体[4-5]、牛顿粘性流体[6]或塑性物质。20世纪70年代，北极冰动力学联合试验（Arctic Ice Dynamics Joint Experiment，ATDJEX）首次提出弹-塑性流变学[7]，于是非线性塑性流变学发展起来[8-9]。1979年，Hibler提出粘-塑性（V-P）流变学海冰模式，该模式已经作为众多海冰模拟和研究的基础，同时，它也成功地应用于北极海冰季节循环特征的数值模拟。

在V-P模式中，方程采用迭代方法求解[5,10]，有效地解决了因计算稳定性限制而被迫在海冰密集区采用的时间步长强约束条件。当计算网格加密时，收敛速度非常缓慢。

粘-塑性海冰本构关系主要因模拟极区海冰变化对全球气候影响而建立。但是因该模型较好地描述了大、中尺度的海冰由于受重叠、堆积、断裂等作用导致的显著流变学特征，同时省略了计算中海冰弹性变形作用产生的影响，将冰应力仅作为应变率函数，因此对大、中尺度下中长期海冰数值模拟和预报具有稳定性好，计算量较小等优点，能很好地再现大应变率下海冰所具有的塑性流动行为。目前，这种基于粘-塑性本构关系的动力学模式在包括极区及副极区在内的大中尺度海冰数值模拟及预报中得到了非常广泛的应用。

自然界中，普遍存在冰隙或冰间水道，大尺度海冰一般承受不了拉应力。为此，对粘-塑性模型中的椭圆屈服函数进行平截，可以避免拉应力产生[5]。此种方法可以简化粘-塑性模型在辐散过程中对拉伸和剪切应力的计算，实际情况与计算结果相当吻合。Zhang[11]在Baltic海冰数值模拟中也采用了平截椭圆屈服函数的方法，取得很好的计算结果。

因为采用了半隐式求解方法，V-P模式在1d时间尺度内，对于因明显变化的强迫场导致的风应力反映不太准确[12]。Hunke等[13]在粘-塑海冰模式中使用条件共扼梯度法改进模式计算效率。另外在流变学中加入了弹性特征，即为弹-粘-塑（E-V-P）海冰模式，E-V-P海冰模式中弹性并不是物理意义的弹性，只是为了计算方便而引入的。这种处理方法避免了以往弹-塑模式[14-15]的复杂性。和V-P模式的对比试验表明[16]：两种模式在长时间尺度积分时，效果基本一致。模式结果与北极浮标资料对比表明，E-V-P模式对短时间内强天气尺度强迫的反映更加准确和迅速。在高密集度海冰覆盖海域，E-V-P模式弹性波对海冰状态的改变并不明显。两种模式冰内应力基本相同：在海冰高密集度海域表现为粘-塑特性，在低密集度海域则显示出近似于自由漂流的特征。在气候系统模式中，E-V-P模式比V-P模式具有更好应用前景。

2 海冰漂移

（1）海冰漂移的动量平衡

位于海洋和大气之间的海冰，受到因冰-气界面湍流运动产生的大气拖曳力、海冰-海水之间的拖曳力、冰区内部不同冰块间和冰块内部的张力以及海面因倾斜造成的应力和海冰运动所产生的科氏力影响。海冰动量平衡表示如下：

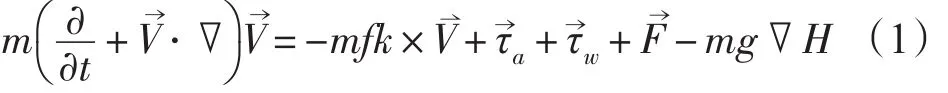
式中：m为海冰在单位面积内的质量。τ→a和τ→w分别是大气和海水对海冰的应力。H是海洋表面动力高度，-mg∇H为倾斜海面梯度力，主要因为海冰的重力位势存在水平的差异而产生的应力。F→是由于冰内应力的变化所引起的内力。

通过观测冬季风应力和水应力，Hunkins[17]做出了海冰动量平衡图（见图1）。在海冰受力平衡中，风应力、水应力、科氏力和冰内力是主要的。风应力和水应力的量级为0.1 N/m2，如果3 m厚冰的冰速为0.1 m/s，则科氏力是0.05 N/m2。3 m厚的冰15 min内可以加速到0.1 m/s，产生惯性力0.1 N/m2。不过惯性振荡引起的加速度项会很大。因为每km冰速变化0.1 m/s需0.1 N/m2力，因此动量平流项很小。海面动力高度梯度项很小，在局地问题研究中可以忽略不计。

研究者们对上述各项的量级大小持有不同的看法。Rothrock[18]对式（1）进行尺度分析：海水应力和风应力比时间变化项大3个数量级，后者可以忽略。在海冰动力学研究中发现，各种力平衡的观测数据和研究结果较为一致。风应力和海水应力是最主要作用力。海冰速度的局地变化、海面倾斜引起的梯度力以及非线性平流项的影响相对比较小，Coriolis力对海冰速度方向影响较大，而对海冰速度值影响较小。在不同条件下，海冰内应力所产生的影响差异较大[19]。近年来，对于海冰内应力（本质是海冰流变学）的研究得到了广泛关注。在动量平衡中，冰内力的作用不容忽视。图2表示在大气边界层的风场和冰下海洋Ekman层海流的作用下，通过冰内应力响应海冰的漂移。

在海冰受力平衡机制中稳定平均流的作用较小，仅为风驱动作用的百分之几。然而在长时间的情况下，流和水位梯度的作用都不能忽视。图3是3个北极漂流站两年位置变化的观测和模拟，清楚表明海流和水位梯度的作用。不考虑冰内应力作用，即所谓“自由漂移”。考察大尺度海冰运动对地转风的响应时[20]，发现北冰洋海冰运动对数月长时间平均海洋环流和地转风具有同等作用；对数天到1个月短时间尺度地转风决定了冰速方差的70%。Martinson等[21]在研究南大洋浮冰块漂移时，发现冰漂移速度大约为风速的3%，约向其左偏23°。

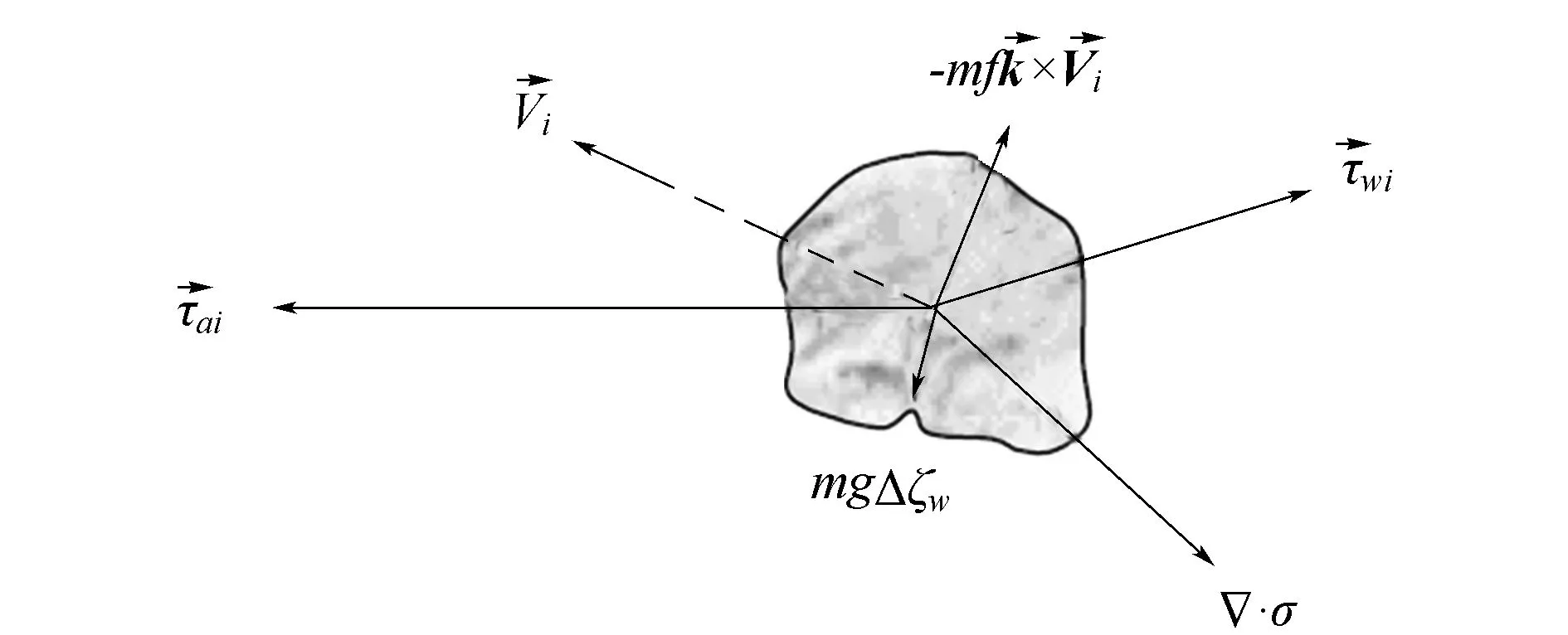
图1 根据观测所作的动量平衡（引自文献[17]）

图2 冰在大气风和海流驱动下通过冰内应力响应而漂移

（2）海冰与大气及海洋的动量交换

在海冰受力平衡中，风应力和海水应力是最大项。冰气界面的动量湍流垂直输送造成风应力。风应力的量值既与冰表面特征有关，也与大气层结状况关系密切。风应力τa包括切向力τ→at和法向力τ→an。τ→an是风作用在水面之上冰侧面的力（见图4），τ→at为冰与气流间摩擦力。τ→at表示为平均风速垂直梯度的函数：

鉴于表面层对数风速分布，上式转换为：

式中：Ca=(kln(z+z0)/z0)2，k=0.4是Karman常数，z0为冰面粗糙高度，一般经验确定，取值为5×10-2±2.5×10-2cm。就上述z0和10 m高的风，阻尼系数Ca=1.64×10-3，其离散度约10%。如不直接给定z0，上述估计的切向应力误差不小于10%。海冰漂移速度比风速小两个量级，所以式（3）中的冰速可以忽略。

上述估计的冰面动力粗糙高度适合于平整冰面。通常覆盖的冰面包括不同程度的堆积冰，从而导致较大的空气阻尼系数。这时，法向应力起重要作用。堆积冰迎风一侧的单位垂直面积受力可用类似于式（3）的公式表示。式中阻尼系数Ca须考虑风向与冰脊轴线的交角φ的订正（见图4）。

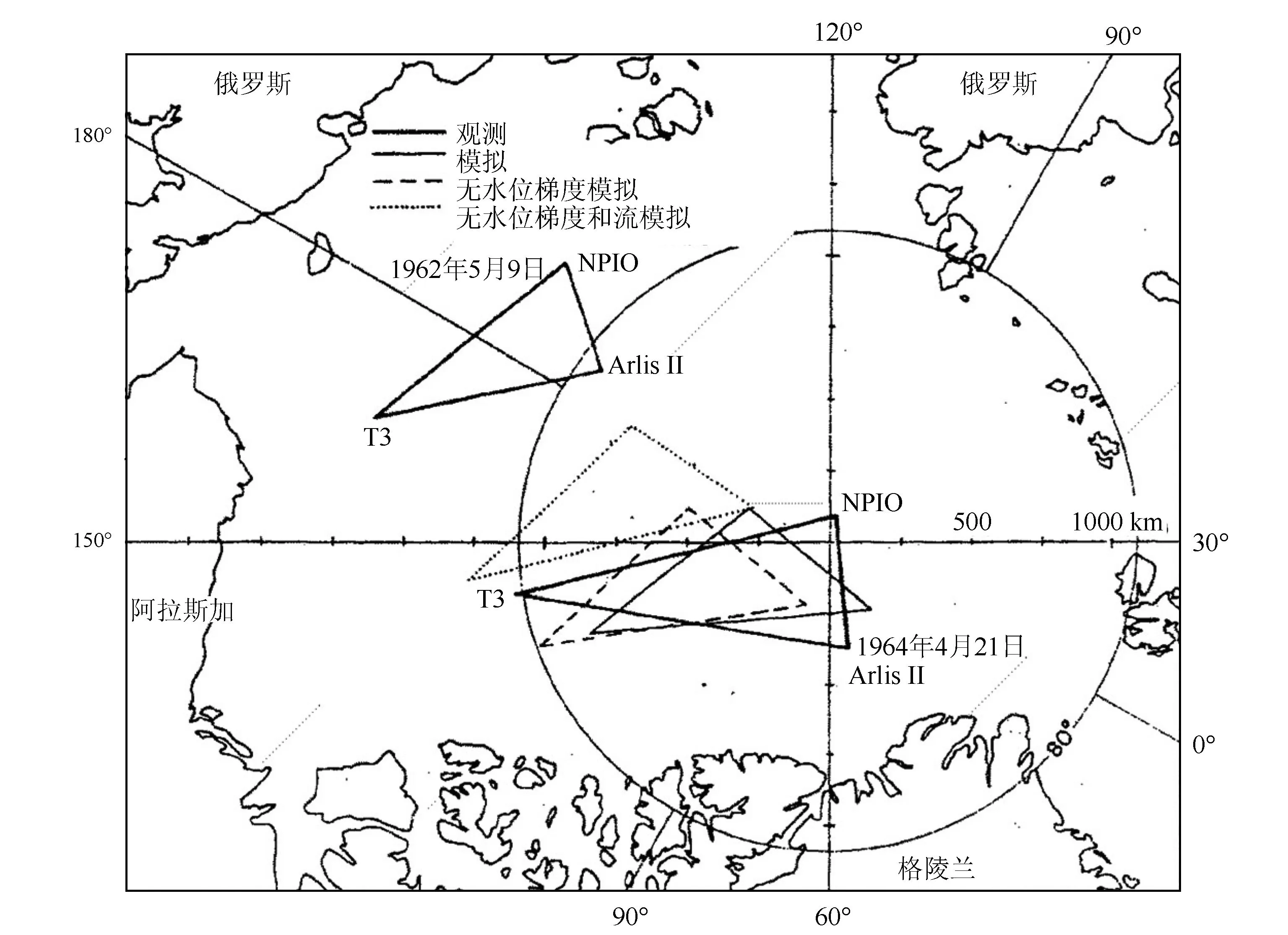
图3 北极3个测流站两年位置变化的观测和模拟（引自文献[22]）

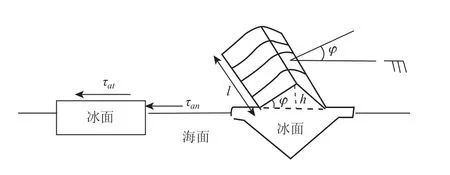
图4 作用于冰面风应力示意图

式中：法向应力的系数Can尚缺野外现场观测资料验证。如果堆积冰脊的总长为l，高为h，则堆积冰脊对风总的阻尼可表示为：

若冰脊侧面和水平面的交角为ψ，那么所有堆积冰脊的底面积可表示为：

对于漂移冰块面积A，其所受法向的风应力为：

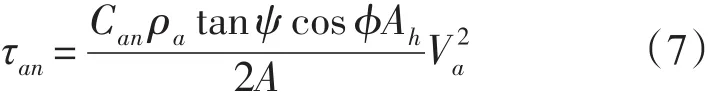
式中：Ah/A是堆积冰与冰盖的面积比，用Nh表示。系数0.5Cntanφ等于堆积冰的阻尼系数3.4×10-2，则Ca=3.4×10-2cosφ。由此可得，冰对风总的阻尼为：

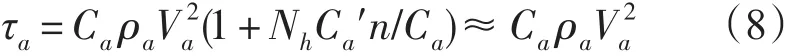
海洋的湍流涡动混合输送造成了冰水间的应力。假定Ekman螺旋层深度与涡动粘性有关并在边界层中线性减小[23]，得到：

式中：Vd是解平衡动力高度和科氏力得到的海洋地转速度，f为科氏参数。在考虑了边界层的非线性特性同时可以更详尽地计算水应力。分析前苏联和美国北极浮冰漂移站的实验结果表明，冰下某邻近层摩擦切应力的垂直变化很小，可表示为：

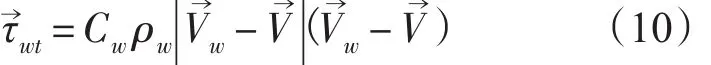
式中：Cw=(k/ln((z+z1)/z1))2；ρw为海水密度，V→W是z处流速，z1为冰下水的动力粗糙度，Karman常数取k=0.4。有人取得较小，如0.1，z1=2.65cm变化范围为0.2～10 cm。一年冰的z1为0.8 cm，冬季平均冰厚为1.5～2.0 cm。当k=0.4，z1=1cm，z=0.5～1m，Cw=0.01时，冰脊潜入水下部分比水面上部分大得多，产生的法向应力相对重要很多。

大尺度冰场承受的风应力和水应力：风场和流场根据海面气压场和海水动力高度场，通过地转关系得到地转风Vg和地转流Vw，同时考虑风和相对流速的扭转偏角ϕ和θ，则：

根据线性关系，式中的Ca′和Cw′取为常数；而非线性关系Ca′和Cw′为风和流的函数，即：

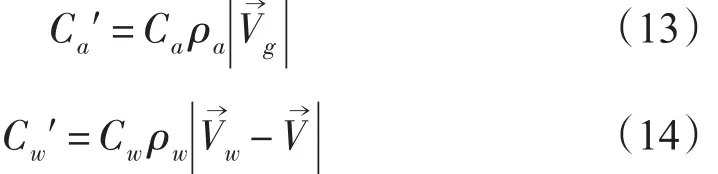
式中：Ca和Cw均为无因次量，Mcphee[24]分别取0.001 2和0.005 5作为典型值。

（3）冰漂移数值模拟

式（1）指出决定海冰漂移的外界强迫主要由风和流驱动，可将冰模式和海洋模式耦合并与大气模式联接，或提供大气风场，模拟大气和海洋对冰漂移的强迫作用。

利用渤海1月海面平均风应力场，模拟不同冰覆盖情况下的渤海冰漂移场，结果表示冰漂移方向偏向风的右方10°～20°，辽东湾中部冰速最大，达到风速的4%，其他海域约为风速的2%～4%，当然也包含风生环流的影响。

将海冰动力学模式应用于渤海并与潮流模式耦合，模拟风与潮共同作用下海冰漂移。图5取自辽东湾4个计算点1个潮周期的冰漂移轨迹，实线是只在潮流作用下的冰漂移轨迹，虚线是风和潮共同作用的模拟结果，非常相似于在辽东湾破冰船跟踪流冰块路径的特点，明显地反映了渤海流冰随椭圆主轴来回漂流，以及风与潮共同作用的特点。Zhang等[25]利用渤海海冰模式和二维渤海潮流模式耦合研究了渤海潮流对冰漂移的影响。

3 海冰形变和冰脊、水道的形成

海冰动力学特性非常依赖于冰强度，随冰厚特性而变化，而冻结、融化、平流和形变过程造成冰厚的变化，即冰厚改变是热力过程和动力过程共同作用的结果。海冰动力过程主要由于形变通过脊化而形成厚冰，通过水道形成而产生开阔水和薄冰。

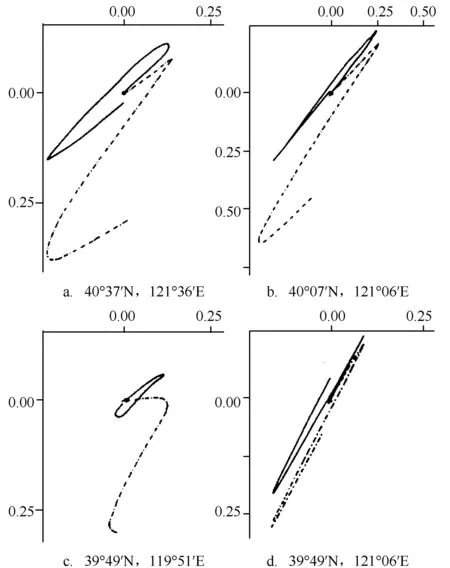
图5 风与潮流共同作用下渤海海冰漂移轨迹的模拟结果

为了表示地球物理尺度造脊过程，Thorndike等[27]引用冰厚分布函数，通过薄冰再分布形成不同类型厚冰。在冰厚分布方程中引用形变再分布函数ψ，表示冰非均匀运动引起水道和压力脊形成的动力学过程，在模式中参数化地表示。形变再分布函数也是应变率张量的函数，如果冰各向同性，则ψ仅依赖与冰速散度和切变有关的两个应变率张量的恒量。假如一块冰被一些不规则裂缝分隔成若干准刚体块，平行于裂缝的位移不影响冰厚分布，但垂直于裂缝位移会引起类似于脊和水道形成的局地形变和冰厚再分布。

冰速场散度引起冰脊和水道形成是显而易见的，图6也明显地表示纯切变作用下仍能出现有些裂缝断开，有些闭合。和纯辐合、辐散形成脊和水道一样，切变也会改变厚度分布。应指出实际冰块内既有气泡又有卤水，以及其他杂质。海冰复杂成分既影响它的热力学特性，又决定它的力学强度，影响它的动力学特性。

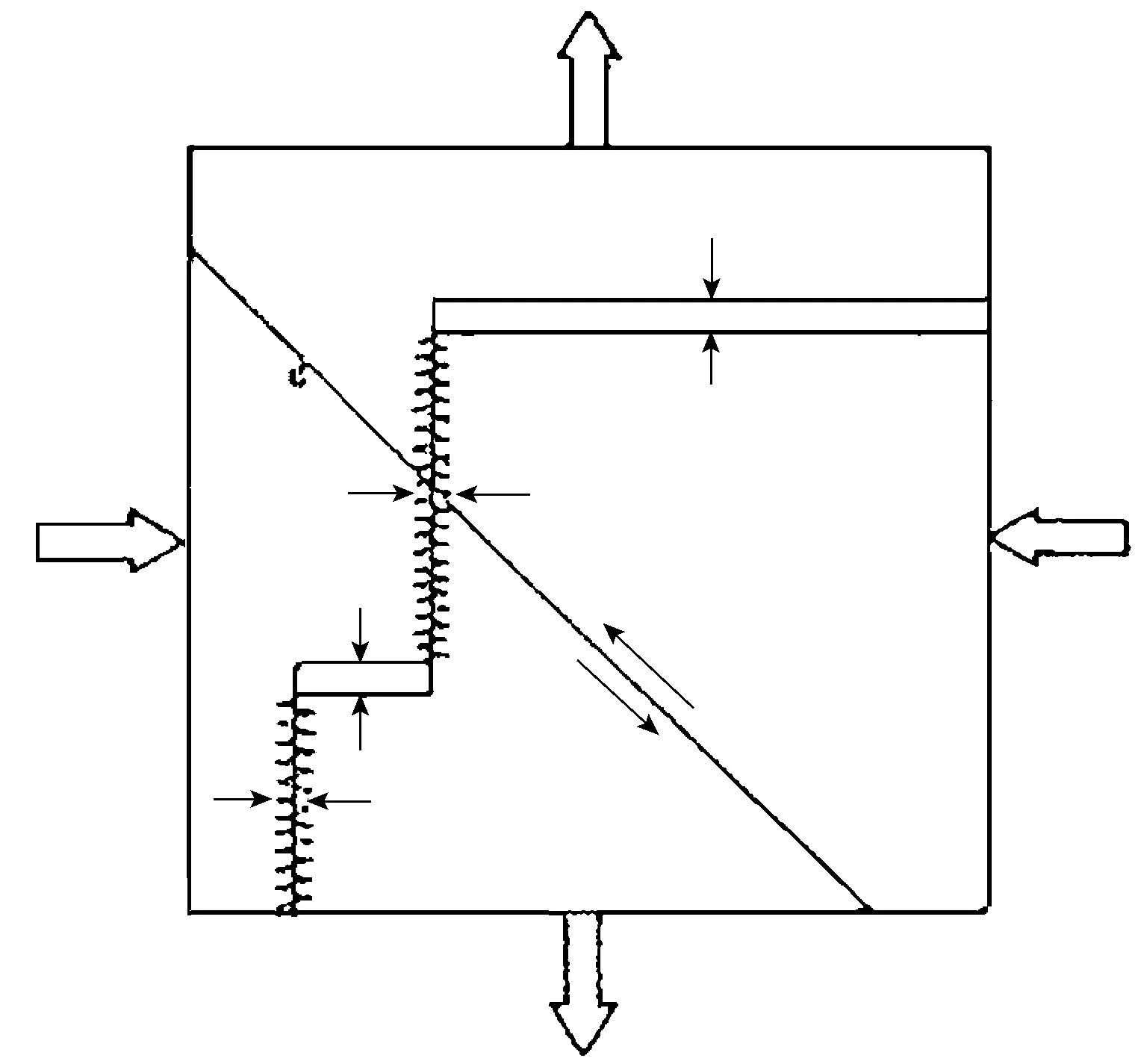
图6 纯切变形变时水道和压力脊形成示意图

海冰模式中采用参数化方法表示非均匀运动引起水道和冰脊形成的动力学过程。将上述模式与大气模式联结，由大气模式和边界层模式提供冰模式海面风场，图7是1993年1月13日的平均堆积冰厚和冰漂移轨迹的3 d和5 d辽东湾预报结果，明显地表示在强东北风驱动下，沿辽东湾西北沿岸海域堆积冰的形成及5 d内迅速发展的过程，预示了该海域堆积冰的形成。该模式还能成功地预报和模拟出水道和辽东湾底开阔水域的形成。

3 海冰流变学

海冰运动的动量平衡分析和数值试验表明，海冰内应力对海冰漂移和形变非常重要。海冰流变学主要探讨海冰切变和抗压断裂的线性和非线性性质、切变和抗压强度的相对量级、冰区内冰块随机碰撞产生的无约束压力项及冰强度与冰厚、冰块大小特征的关系等。

（1）本构关系

海冰的变形与海冰内应力关系密切，根据形变场可以确定内应力。在早期海冰季节变化数值模拟中采用速度相关方法近似这种作用：Parkinson等[3]采用了迭代订正方法，即所谓“空化模型”[9]；更合理方法是根据海冰流变学，即采用海冰形变和厚度与冰内应力关系的本构定律进行科学计算。

海冰是非连续介质，在足够大的空间尺度上，可以被近似地描述为二维连续介质，最普遍的本构关系表示为[28]：

图7 1993年1月13日渤海辽东湾堆积冰形成及冰漂移

式中：σij是二维应力张量，εij是二维应变率张量，δij是Kronecker算子，ζ和η是块体和切变粘性系数，εkk=trεij=ε11+ε22，p是压力项，p、ζ和η通常为应变率张量的恒量的函数。其正应力和偏应力分别为：

这种本构关系既包含粘性流变学又包含塑性流变学。在粘性流变学中，只有形变才能有应力，流量的耗散是不可逆的。在塑性流变学中，非形变或能量耗散可逆形变（即弹性形变）也可维持应力。在海冰研究中，通常采用流变学的特殊情形：

（a）线性粘性模型

对于线性粘性，应力与应变率成线性关系，p、ζ和η是常数。

理想固体塑性：应力状态不定或与应变率无关，应力状态是固定的，ζ和η与应变率恒量成非线性关系；对零应变率状态不能确定ζ和η，此时为刚体运动，由外力平衡决定内应力。

海冰的线性粘性流变学允许两种应力状态，即切变粘性（Newton粘性，η=常数，ζ=p=0）和块体粘性（ζ=常数，η=p=0）。

对于切变粘性

其应变率张量为：

或：

应变张量为：

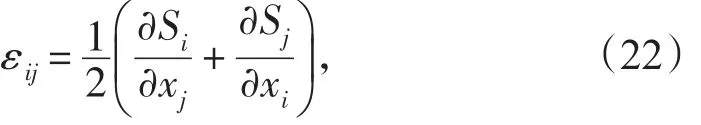
式中：Si为位移分量。

对块体粘性，介质对膨胀和压缩有阻尼，对切变无阻尼，因此

既包含切变粘性又包含块体粘性的更为一般的线性粘性情况

或

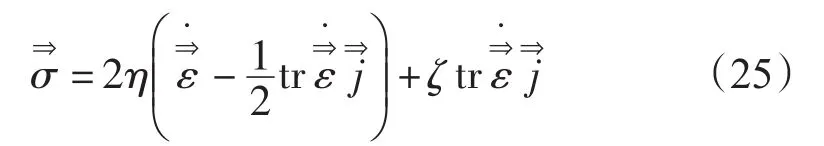
式中：j是单位张量。Glen提出海冰对压缩的阻尼大，而对拉伸的阻尼小。

忽略粘性梯度，则内应力F为：

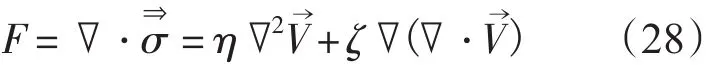
即

该式已经应用于海冰漂移模式中，通过附加屈服判据考虑当海冰密集度接近于1时的塑性性质。

（b）弹-塑性模型

线性弹性本构定律也被用于海冰动力学研究。理想的弹性过程是等温过程，当外力撤除时可回复到初始状态。由于大尺度海冰变形几乎总是不可逆，对海冰而言，线性弹性甚至非线性弹性假定通常都不合理，通常海冰表现为塑性性质。Coon等[7]提出弹-塑性本构关系，采用弹-塑性材料的屈服判据确定是否出现塑性性质。

即：当F(σ1,σ2)＜0时为弹性，当F(σ1,σ2)=0时为塑性。

式中：F(σ1,σ2)为屈服条件。

AIDJEX研究组曾提出新屈服判据：

在弹-塑性模式中，假定弹性性质是线性和各向同性的，则屈服函数为圆屈服函数：

于是得到：

这里

该关系常用于拉格朗日模式中，数学处理比较复杂。

图8 海冰塑形流变学的屈服曲线

（c）粘-塑性模型

对于理想塑性本构定律，应力状态位于某种固定屈服曲线之上或其内，即图8表示的椭圆屈服曲线。对塑性流变学来说，应力状态和应变率成唯一关系，最一般的关系为给定应力状态，应变率之比是垂直表面的矢量之比，即所谓的法向流定律。对于刚体运动，应力状态位于椭圆内，上述两种线性粘性定律允许大的抗压强度（即正压力）。然而，这种特殊塑性定律仅允许小的抗拉强度。Hibler[5]将海冰当作非线性粘性可压缩流体，提出粘-塑性本构定律，这是最一般情况的流变学。冰内压力与冰厚、密集度相关，可表示为：

式中：η和ζ分别表示非线性切变和块体粘性，可写作：

因此冰内应力可表示为：

采用粘-塑性流变学对于强非线性海冰动力学数值模拟是很有效的方法，其原因在于它能有效避免弹-塑性流变学中弹性波所引起的问题[29]，在固定欧拉网格上可以更容易导出差分方程。当模式采用隐式方案时，可以选取较大时间步长，这样非常有利于模拟海冰长期季节性变化。Pritchard[14]指出，粘-塑性流变学比弹-塑性流变学包含着更普遍的本构关系，同时粘-塑性流变学也适用于冰边缘带研究。

图9表示了几种流变学的比较情况。对于线性粘性，应力与形变率成正比；塑性流变学无论对于大的形变率还是小的形变率，冰块都允许相当大的应力，另外它还允许冰能强抗压和切变形变，但只允许几乎没有形变的膨胀。图9还表明：

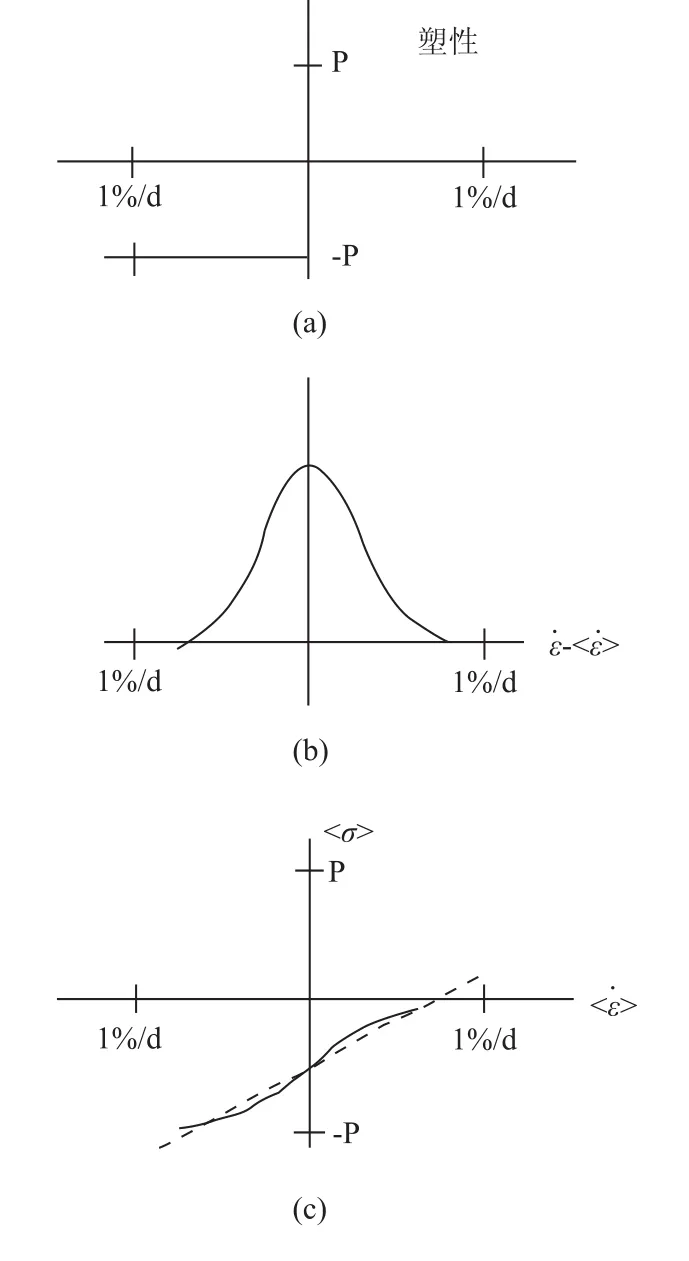
图9 几种流变学的比较情况

（1）在弹-塑性情况下，冰抗压应力不变，而且对辐散应变无阻尼；

（2）在粘-塑性情况下，具有类似性质，但应力状态由形变率而不是由应变率来决定；

（3）上述两种塑性和线性粘性的不同在于，即使对于小的应变率，应力也可相当大，并且除了很小的形变率外，应力与形变率无关。另外，在弹-塑性情况下，无任何冰的相对运动，强应力也能维持。

（d）海冰碰撞流变学

Shen等[30-31]和Lu[32]应用粒状流体理论于海冰边缘带的海冰运动，并假定海冰运动象“刚体微粒流”那样，系统内通过碰撞来传递动量消耗动能。Shen等[30]对格陵兰海资料分析发现，观测结果与根据碰撞流变学预报的冰速变化之间相关很大。

碰撞流变学假定流冰块为均匀圆盘，由冰速随机变化产生碰撞，碰撞频率依赖于冰速大小和密集度，碰撞性质用回复（或非弹性）系数表征，碰撞产生的应力受动量变率控制，在系统内转换，因此应力与流冰块质量成正比。为闭合系统，还需要确定随机速度变化面，根据冰形变的能量耗散，通提供冰速变化面的机械能方程来进行。因此假如形变为0，则变化面和应力为0。

应力与质点碰撞转换平均动量的关系为：

式中：σmn是垂直于Xm的面上，作用于Xn方向的应力。pm是垂直于Xm的单位面积的质点数，f为每个质点的碰撞频率是方向每次碰撞的平均动量输送。为了利用粒子流理论得到冰应力场，需要知道以下3个因子：所考虑面上的流冰块数，每块的碰撞频率，每次碰撞的动量输送。因为冰块的大小和形状变化多样，所以又假定：所有冰块具有相同形状，即盘形；所有冰块具有同样的物理性质（密度、盐度、孔隙率和温度等）；在同一计算网格上，冰块具有相同厚度。

（e）空化流体模型

冰内应力依赖于表示冰速（形变）和外强迫之间关系所选取的特殊参数。空化流体流变学是一种特殊参数化方法，在数值模拟中考虑海冰最主要特性。它是在考虑海冰大尺度性质基础上经过某些简化假定而得到的。其基本假定是：将冰当作理想的两相介质，一相为几乎没有强度的开阔水，另一相为相当硬的冰；这种理想化介质没有切变和抗拉强度，当辐散时允许开阔水的覆盖面积自由地增加（海冰密集度减小），而当压缩时，由于“刚体”位相的原因，这种介质具有某种阻尼。但冰位相不是完全刚体，它有可压缩强度，当超过此强度，海冰可以辐合和增厚，这种可压缩强度是海冰厚度合密集度的函数。这样的理想性质非常便于数学处理。

（2）不同流变学的对比试验

（a）粘-塑性流变学参数敏感性试验

粘-塑性流变学已较广泛地应用于不同海冰模式，其椭圆屈服曲线各种参数的重要性已引起许多学者重视。各模式所采用参数差别也较大，且至今尚无定论[33]，应用上述模式，采用海冰粘-塑性流变学模拟加拿大东海岸拉布拉多海域海冰漂移，并试验椭圆屈服曲线主要控制参数冰强度参数P*对模拟冰速的影响。当P*减小，模拟的冰速增大；反之，P*增大，冰速减小。

（b）不同流变学对冰边缘带（Margrinal Ice Zone，MIZ）海冰的动力学影响

Zhang[34]利用理想的MIZ海冰模式，采用浮冰块碰撞，Hibler粘-塑性和Mohr-Coulomb 3种流变学本构关系计算冰内应力。第1种海冰看作为一种微粒流体，而后两者看作为塑性流体。给定风场强迫，模拟结果显示冰流变学对MIZ冰漂移有明显影响（见图10）。

（c）不同屈服曲线对浮冰线性运动学特性的影响

Wang[35]根据浮冰块内应力场的特性分析发展了一种压缩浮冰的屈服曲线观测方法。分析指出屈服曲线斜率和线性运动学特性（Linear Kinematic Features，LKFs）的交叉角有关。因此根据这种交叉角测量可以反演屈服曲线。Wang等[36]进一步利用2-level粘-塑性海冰模式研究不同模式网格分辨率和不同屈服条件对浮冰块线性运动学特性（LKFs）模拟的影响。采用的网格分辨率包括10.5和2 km，采用3种屈服曲线（椭圆、修正的Coulomb及弯曲菱形屈服曲线，见图11）。应用NCEP/NCAR再分析风场资料，并采用RADARSAT GPS海冰运动资料做比较。结果显示应用弯曲的菱形屈服曲线，LKFS能很好地再现，而应用修正的Coulomb屈服曲线，增加网格分辨率仅能稍改进LKFS模拟结果。图12采用2 km格距，稳定风场3种不同屈服曲线模拟的最大切应变率(MSSR)和用RGPS处理得到MSSR的比较。

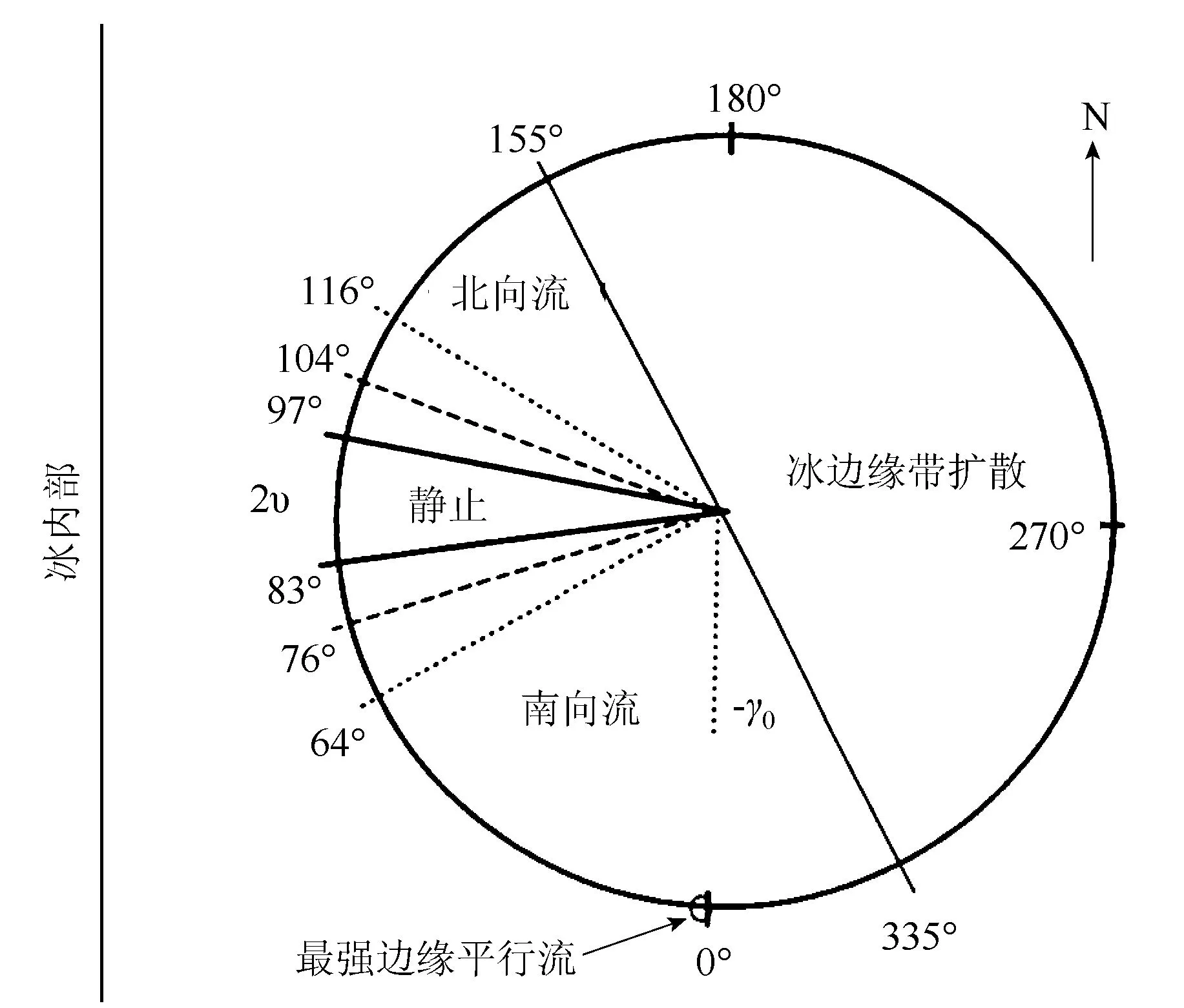
图10 冰边缘带定常风场不同流变学本构关系对MIZ冰运动的影响

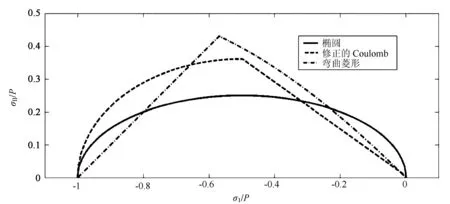
图11 模拟中所采用的3种屈服曲线椭圆（实线），修正的Coulomb（虚线）及弯曲菱形（点虚线）

图12 1997年12月5—11日MSSR场的比较（网格距为2 km；稳定风场引自文献[36]）

4 讨论

在上述不同的海冰动力学本构模型中，应用最广泛的是Hibler的粘-塑性本构关系，它不仅应用于极区及边缘区域的大尺度海冰数值模拟，还应用于像Baltic海、渤海等中尺度海冰的数值研究及数值预报。Hunke等在粘-塑海冰模式基础上发展了弹-粘-塑海冰模式，可以采用较大时间步长的显式差分计算，进而可用于海冰动力学的并行计算，在气候系统模式中得到了越来越广泛应用。另外，基于海冰碰撞流变学的颗粒流模型可以应用于小尺度冰块间的碰撞、堆积、断裂和重叠等过程的数值模拟，其优点在于物理意义明确，计算精度高，但因其计算量很大，从而限制了它在大、中尺度海冰动力学的数值模拟。

[1]Felzenbaum A I.The theory of steady drift of ice and the calculation of the long period mean drift in the central part of the Arctic Basin[J].Problems of the North,1961,2:13-44.

[2]Bryan K,Manabe S,Pacanowski R C.A global ocean-atmosphere climate model.Part II.The oceanic circulation[J].Journal of Physical Oceanography,1975,5(1):30-46.

[3]Parkinson C L,Washington W M.A large-scale numerical model of sea ice[J].Journal of Geophysical Research,1979,84(C1):311-337.

[4]Hibler III W D.Differential sea-ice drift.II.comparison of mesoscale strain measurements to linear drift theory predictions[J].Journal of Glaciology,1974,13(69):457-471.

[5]Hibler III W D.A dynamic thermodynamic sea ice model[J].Journal of Physical Oceanography,1979,9(4):815-846.

[6]Campbell W J.The wind driven circulation of ice and water in a polar ocean[J].Journal of Geophysical Research,1965,70(14):3279-3301.

[7]Coon M D,Maykut G A,Pritchard R S,et al.Modeling the pack ice as an elastic-plastic material[J].AIDJEX Bulletin,1974,24:1-105.

[8]Pritchard R S,Coon M D,McPhee M G.Simulation of sea ice dynamics during AIDJEX[J]. Journal of Pressure Vessel Technology,1977,99(3):491-497.

[9]Flato G M,Hibler III W D.Modeling pack ice as a cavitating fluid[J].Journal of Physical Oceanography,1992,22(6):626-651.

[10]Holland D M,Mysak L A,Manak D K,et al.Sensitivity study of a dynamic thermodynamic sea ice model[J].Journal of Geophysical Research,1993,98(C2):2561-2586.

[11]Zhang Z H.Comparisons between observed and simulated ice motion in the northern Baltic Sea[J].Geophysica,2000,36(1-2):111-126.

[12]Häkkinen S,Mellor G L.Modeling the seasonal variability of a coupled Arctic ice-ocean system[J].Journal of Geophysical Research,1992,97(C12):20285-20304.

[13]Hunke E C,Dukowicz J K.An elastic-viscous-plastic model for sea ice dynamics[J].Journal of Physical Oceanography,1997,27(9):1849-1867.

[14]Pritchard R S.An elastic-plastic constitutive law for sea ice[J].Journal ofApplied Mechanics,1975,42(2):379-384.

[15]Colony R,Pritchard R S.Integration of elastic-plastic constitutive laws[J].AIDJEX Bulletin,1975,30:55-80.

[16]Hunke E C,Zhang Y.A comparison of sea ice dynamics models at high resolution[J].Monthly Weather Review,1999,127(3):396-408.

[17]Hunkins K L.Substance eddies in the Arctic Ocean and baroclinic instability[M]//Weller G,BoWling S A.Climate of the Arctic.Fairbanks:UniversityAlaska,1975:398-406.

[18]Rothrock D A.The steady drift of an incompressible Arctic ice cover[J].AIDJEX Bulletin,1973,21:49-77.

[19]Steele M,Zhang J L,Rothrock D,et al.The force balance of sea ice in a numerical model of the Arctic Ocean[J].Journal of Geophysical Research,1997,102(C9):21061-21079.

[20]Thorndike A S,Colony R.Sea ice motion in response to geostrophic winds[J].Journal of Geophysical Research,1982,87(C8):5845-5852.

[21]Martinson D G,Wamser C.Ice drift and momentum exchange in winter Antarctic pack ice[J].Journal of Geophysical Research,1990,95(C2):1741-1755.

[22]Hibler III W D,Tucker W B III.Some results from a linearviscous model of the Arctic ice cover[J].Journal of Glaciology,1979,22(87):293-304.

[23]Reed R J,Campbell W J.Theory and observations of the drift of ice station alpha[R].Washington:Department of Meteorology,University of Washington,1960:255.

[24]McPhee M G.Ice-ocean momentum transfer for the AIDJEX ice model[J].AIDJEX Bulletin,1975,29:93-111.

[25]Zhang Z H,Wu H D.Numerical study on tides and tidal drift of sea ice in the ice-covered Bohai Sea[M]//Yu Z,Tang C L,Preller R H,et al.Sea Ice Observation and Modeling.Proceedings of Beijing’93 International Symposium on Sea Ice.Beijing:China Ocean Press,1994:34-46.

[26]Wu H D,Bai S,Zhang Z H,et al.Numerical simulation for dynamical processes of sea ice[J].Acta Oceanologica Sinica,1997,16(3):303-317.

[27]Thorndike A S,Rothrock D A,Maykut G A,et al.The thickness distribution of sea ice[J].Journal of Geophysical Research,1975,80(33):4501-4513.

[28]Glen J W.Thoughts on a viscous model for sea ice[J].AIDJEX Bulletin,1970,2:18-27.

[29]Colony R,Rothrock D A.A perspective of the time-dependent response of the AIDJEX model[M]//Pritchard R S.Sea Ice Processes and Models.Washington:University of Washington Press,1980:124-133.

[30]Shen H H,Hibler W D,Leppäranta M.On applying granular flow theory to a deforming broken ice field[J].Acta Mechanics,1986,63(1-4):143-160.

[31]Shen H H,Hibler III W D,Leppäranta M.The role of floe collisions in sea ice rheology[J].JournalofGeophysical Research,1987,92(C7):7085-7096.

[32]Lu Q M.On mesoscale modelling of the dynamics and thermodynamics of sea ice[R].Copenhagen:Technical University of Denmark,1988:50-73.

[33]吴辉碇,白珊,张占海.海冰流变学[M]//蒋伯城,张锁春.高科技研究中的数值计算.长沙:国防科技大学出版社,1995:40-49.

[34]Zhang Z H.Effect of different rheologies on sea ice dynamics[J].Report Series in Geophysics,University of Helsinki,1998,40:39-72.

[35]Wang K G.Observing the yield curve of compacted pack ice[J].Journal of Geophysical Research,2007,112(C5):C05015,doi:10.1029/2006JC003610.

[36]Wang K G,Wang C X.Modeling linear kinematic features in pack ice[J].JournalofGeophysicalResearch,2009,114(C12):C12011,doi:10.1029/2008JC005217.

Sea ice dynamics

LIU Yu，WU Hui-ding
（National Marine Environment Forecasting Center,Key Laboratory of Research on Marine Hazards Forecasting,Beijing 100081 China）

In this paper,the development of sea ice dynamics is briefly reviewed.The dynamic processes of sea ice drift,deformation and accumulation are introduced.The applications of different sea ice constitutive equations in sea ice rheology are compared and analyzed.

sea ice；dynamics；rheology；constitutive equations

P731.15

A

1003-0239（2017）05-0099-12

10.11737/j.issn.1003-0239.2017.05.011

2017-09-22；

2017-10-09。

国家重点研发计划（2016YFC1401502）；国家自然科学基金（41676189；41506109）。

刘煜（1973-），男，副研究员，硕士，主要从事海冰预报和研究工作。E-mail：liuyu@nmefc.gov.cn