贺兰山云杉林根土复合体提高边坡稳定性分析

田 佳，及金楠，钟 琦，余鹏程，杨丽娇，袁 博



贺兰山云杉林根土复合体提高边坡稳定性分析

田 佳1，及金楠2，钟 琦1，余鹏程1，杨丽娇1，袁 博1

（1. 宁夏大学农学院，银川 750021；2. 北京林业大学水土保持学院，北京 100083）

为了研究贺兰山青海云杉林（）边坡根土复合体对边坡稳定性的影响，该文在直剪试验、三轴试验等获得的土壤参数基础上，建立了基于有限元理论的贺兰山青海云杉林边坡稳定性计算数值模型，并在5种坡度条件下（18.43°、21.80°、26.57°、33.69°、45.00°）计算了无林边坡和有林边坡的安全系数、最大塑性应变、最大位移、破坏时间及它们的增长率随坡度的变化规律，并计算了土壤强度参数摩擦角、黏聚力、剪胀角与安全系数的灰色关联度矩阵和平均关联度。结果表明：1）无林边坡与有林边坡的安全系数随坡度的变化规律是一致的，都以幂函数递减。有林边坡相对于无林边坡安全系数的增长率以指数函数增加，且坡度越陡根土复合体对边坡稳定性的提高作用越强；2）根土复合体的存在可以延长边坡的破坏时间，有林边坡的破坏时间均高于无林边坡，根土复合体提高边坡破坏时间的增长率随坡度的增大呈抛物线增加，且坡度越陡提高作用越明显。边坡破坏时有无塑性贯通区会明显改变最大塑性应变、最大位移、破坏时间的值；3）摩擦角、黏聚力、剪胀角3个土壤强度参数中，黏聚力是影响边坡稳定的主导因素，摩擦角、剪胀角的影响次之，此规律不受边坡坡度的影响，这是根土复合体可以显著影响边坡稳定性的根本原因之一。该文的研究结果对于解释森林根土复合体加固边坡作用的本质、推进边坡稳定性计算的数值模拟、防治贺兰山浅层滑坡及水土流失灾害都具有重要的意义。

边坡稳定性；土壤；数值模拟；根土复合体；贺兰山；青海云杉

0 引 言

宁夏贺兰山地处中国温带草原区与荒漠区的过渡地带，是中国西北干旱风沙地区典型的温带山地森林生态系统，是银川平原的生态屏障和水源涵养区，也是重要的风景名胜区。贺兰山地质条件复杂，植被盖度较低，属于宁夏政府公布的水土流失较严重区域[1-2]。部分地区发生了严重的崩塌、滑坡和泥石流灾害，造成了巨大的经济损失。国内外很多学者研究表明，植物根系及其形成的根土复合体具有防治浅层滑坡和减少土壤侵蚀的作用[3-7]，植物护坡作为工程护坡措施的辅助手段目前已经广泛应用于各类边坡防护工程当中。采用植物护坡具有防治成本低、景观效果和环境效益突出等优点[8]，在越来越注重生态环境保护、人与自然和谐发展的今天，正逐步成为国内外普遍采用的浅层滑坡和水土流失治理技术[9]。青海云杉（）、油松（）和山杨（）是贺兰山最主要的3种乔木树种，在调节气候、保持水土尤其是稳定边坡方面发挥着非常重要的作用[10]。

与野外和室内试验相比，数值模拟在时间、费用、复杂程度和可重复性上具有较大的优势，是一种非常有前景的研究根系固土作用的方法[11]，特别是基于有限元理论（Finite element theory）的数值模拟方法由于其模拟精度较高，目前已有很多学者采用。如：Dupuy等[12]利用ABAQUS通用有限元分析软件研究了风力荷载下的根系锚固土壤作用；Lin等[5]采用数值模拟的方法研究了台湾桂竹（Makino bamboo）对浅层滑坡的防治作用；Fan等[13]采用PLAXIS 3D有限元软件建立了根系护坡的三维有限元模型，并基于强度折减法（strength reduction method）研究植物的空间分布（株行距）对边坡稳定性的影响；Chok等[11]和Ji等[9]研究了根系附加黏聚力等因素变化对边坡安全系数的影响等。这些研究结果不仅证实了根土复合体确实有明显的加固边坡效果，而且也证实了有限元数值模拟结果与野外和室内试验获得的数据相比具有很高的可靠性。

本文以贺兰山苏峪口青海云杉纯林的根土复合体为研究对象，通过室内直剪试验、三轴试验获得土壤参数，在此基础上建立基于有限元理论的贺兰山青海云杉林边坡稳定性计算数值模型，并在5种坡度条件下（=18.43°、21.80°、26.57°、33.69°、45.00°）计算了无林边坡和有林边坡的安全系数F，最大塑性应变PEMAGmax、最大位移max、破坏时间及它们的增长率随边坡坡度的变化规律；同时本文计算了土壤强度参数、、与边坡安全系数F的灰色关联度。本文的研究结果对于解释森林根土复合体加固边坡作用的本质、推进边坡稳定性计算的数值模拟、防治贺兰山浅层滑坡及水土流失灾害都具有重要的意义。

1 材料与方法

1.1 研究地点

研究地点位于宁夏贺兰山苏峪口国家森林公园兔儿坑护林点（38°44′07.43″N；105°54′39.10″E；海拔2 313 m）。研究区属典型温带大陆性山地气候，年均气温−0.9 ℃，年均降水量287.2～429.8 mm，且主要集中在7－9月。主要森林植被包括：青海云杉（）、油松（）、山杨）、白桦（）、灰榆（）和小叶金露梅（）等[11]。土壤类型从上而下依次是山地草甸土、山地灰褐土、山地灰钙土、粗骨土和荒漠土。

1.2 土壤的采集

在兔儿坑青海云杉纯林随机抽取10株青海云杉，测量胸径、树高、冠幅、树龄，选取与平均值最为接近的3株作为标准木（表2）。以树干中心为圆心，距离为1.0 m的四周内用环刀（120 cm3）对土壤进行取样，共分5层，0～10，>10～20，>20～30，>30～40和>40～50 cm，每层取3次重复。土壤含水率采用烘干法测定（温度设定为105 ℃，时间为12 h）。土壤机械组成采用筛分法，重复3次求平均值后得出各粒径组百分含量，如表1所示。本文土壤含水率和土壤机械组成的测定参考国家标准GB-T50123-1999进行[14]。

表1 土的粒径级配

1.3 直接剪切试验

在本文中青海云杉林根土复合体和素土（不含根的土）均为原状土，且均为同一次野外采样获得。因此，通过室内试验所获得的土壤各参数均代表了野外坡面土壤的实际情况。本文不对土壤进行室内重塑的另一原因是重塑土很难做到模拟野外原状的含根土和素土在土壤物理性质上的差别[15]。室内直剪试验采用南京土壤仪器厂生产的ZJ型应变控制直剪仪，剪切速度设定为0.8 mm/min（快剪），每组试验做4个荷载的试样（12.5，25，50，100 kPa），每个荷载下做3个重复。3个重复的抗剪强度均值作为该荷载下的抗剪强度。通过抗剪强度与垂直荷载的关系曲线，求出根土复合体黏聚力值和摩擦角值（包括素土），并作为土壤强度参数输入到边坡稳定性数值模型中。在该试验中按照土体自重压力公式推求试验所用的垂直荷载，作者认为这样更符合野外的实际情况。具体计算：土壤的容重16.1 kN/m3×0.75 m（土层厚度的一半，也是主要含根层）=12.08 kPa，试验中取12.5 kPa作为第1级垂直荷载；16.1 kN/m3×1.5 m（土层总厚度）=24.15 kPa，试验中取25 kPa作为第2级垂直荷载，参照直剪试验的要求选取其余的两级垂直荷载为50、100 kPa。本文直剪试验的具体步骤参照《土工实验方法标准GB/T50123-1999》执行[14]。

1.4 边坡稳定性计算有限元模型的建立

该研究中采用通用有限元软件ABAQUS构建青海云杉林边坡的数值模型。模型的几何尺寸和边界条件如图1所示，边坡高2（=10 m），坡顶与坡脚长，坡面长（变量），土层厚h=1.5 m，土层以下为岩石（砂岩）。为了模拟不同坡度的青海云杉林边坡，通过变换坡面长来改变坡角，模型中分别为18.43°、21.80°、26.57°、33.69°、45.00°，即∶H=3∶1、2.5∶1、2∶1、1.5∶1、1∶1。边坡侧面方向约束、底面完全约束，边坡表面为自由面不做任何约束。考虑到林木的自重，对模型施加林木产生的附加重力荷载（表2），并以体力（Body force）的方式加载。模型中土壤被定义为理想弹塑性材料，遵循Mohr-Coulomb（摩尔库伦）屈服准则，并采用六结点修正二次平面应变三角形单元，孔压、沙漏控制（CPE6MP）划分坡面土壤，因为坡面土壤是本文主要的研究对象所以网格划分较细（边长0.5 m）；采用平面应变三角形单元（CPE3）划分基岩（岩石），由于岩石不是本文的研究区域，且岩石在模型中的变形很小（因为弹性模量很大）所以采用较粗的网格划分（边长0.5～4 m），这样做可以节省计算时间，同时不会影响到计算精度。本文所建立的数值模型网格数从1 014～2 081（边坡坡度不同网格数不同）。

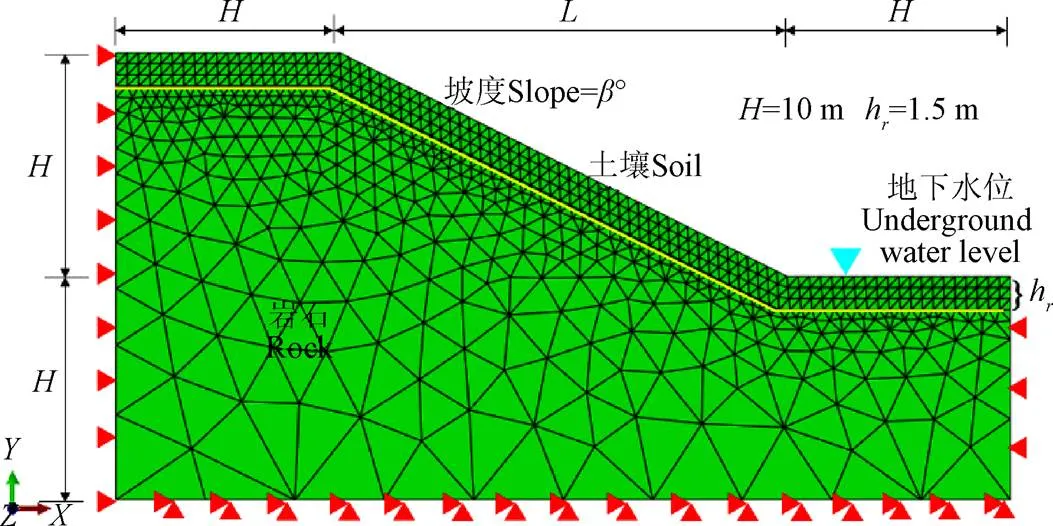
注：边坡高为2H（H=10 m）；L为坡面的长度（变量），hr为土层的厚度，单位m。土壤网格单元类型为CPE6MP；岩石网格单元类型为CPE3.

1.5 边坡安全系数计算方法

本文采用强度折减法（Strength reduction method, SRM）[16]进行边坡稳定性分析。折减后的抗剪强度参数可以分别表示为

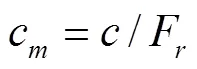
式中和是土壤所能提供的抗剪强度，单位分别为kPa和(°)；c和φ是维持平衡所需要的或者土壤实际发挥的抗剪强度，单位分别为kPa和(°)；F是强度折减系数。计算中假定不同的强度折减系数F，根据折减后的强度参数进行有限元分析。在整个过程中不断增加F，当达到临界破坏时的强度折减系数就是边坡安全系数F。判断边坡是否达到临界点可以通过计算是否收敛、特征部位的位移拐点和是否形成连续的塑性贯通区进行判断，在本文中采用观察数值计算是否收敛（不收敛）作为边坡失稳临界状态的标准[16]。

表2 青海云杉林自重计算

注：表中重力加速度取10 N·kg-1。

Note: Gravity acceleration in table is 10 N·kg-1.

1.6 灰色关联度计算

本研究中通过变换土壤强度参数（摩擦角、黏聚力、剪胀角），分析土壤强度参数对边坡安全系数F的影响，从而找出导致边坡失稳的主导因素。文中采用灰色系统理论中的灰关联分析方法对边坡安全系数进行敏感性因素分析。文中的灰色矩阵以影响边坡稳定的土壤强度参数（、、）为比较矩阵、以边坡的安全系数为参考矩阵。

式中为影响边坡稳定因素的数目，为各因素变化值数目，在本文中采用区间相对值法对数据矩阵进行无量纲化[17]。

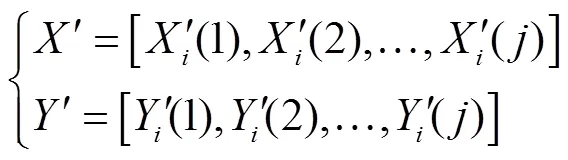
式中

灰色关联度的计算公式为：

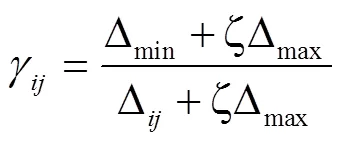
式中为分辨系数，取值在0～1之间，本文中取0.5。式中

由于关联系数的个数较多，信息比较分散，不便于比较，因此求γ的平均值作为关联度即平均关联度Γ，作为影响因素关联性的比较。平均关联度可用下式求得

2 结果与分析

2.1 模型参数试验结果

通过直接剪切试验测定青海云杉林根土复合体、素土（不含根的土）的黏聚力、内摩擦角；通过三轴压缩试验（不固结不排水，剪切速率0.8 mm/min）测定弹性模量（试验结果表明根土复合体与素土的弹性模量基本没有差别（图2））；以及通过其他相关的配套试验确定了有限元数值模型中土壤的各参数（表3）。经过现场调查，兔儿坑青海云杉林基岩为砂岩，平均土层厚度h=1.5 m。砂岩力学特性参数参考谢仁海等[18]主编的《构造地质学》。从表3中可以看到由于土壤中含有根系，导致了土壤的摩擦角、干（湿）密度的减小；但是土壤的黏聚力、孔隙比、含水率有明显的增加。在本文的分析计算中，土壤剪胀角的初始值都设定为0.1（ABAQUS软件默认值）。

表3 数值模拟中的土壤和岩石参数

注：右上角有参考文献标注的，表明参数取值来自于文献。

Note: Upper right corner is annotated with reference, indicating that parameter values are derived from literatures.

注：ε1/(σ1-σ3)表示轴向应变比主应力差，弹性模量E是图中直线与纵坐标的截距的倒数，即E=1/0.000 3≈3 MPa.

2.2 数值模拟结果

2.2.1 无林和有林边坡的安全系数及增长率随坡度的变化规律

文中利用有限元模型分别计算了坡度为18.43°、21.80°、26.57°、33.69°、45.00°，5种情况下的无林和有林（青海云杉林）边坡的安全系数、最大塑性应变PEMAGmax、最大位移max，及它们的增长率，计算结果见表4。图3反映了边坡安全系数随坡度的变化规律，可以看出有林和无林边坡的变化规律是一致的，都符合幂函数的变化规律，安全系数随着坡度的增大而减小（其中：无林：=65.089-1.001，2=0.996 7；有林：=46.775-0.813，2=0.998 7）。有林边坡相对于无林边坡安全系数的增长率随着坡度的增加而增大，并呈现出指数函数变化规律（=1.6704e0.0239x，2=0.933 9）。边坡的安全系数随坡度的增加而减小，这一现象已经被众多学者所证实[5,9,11,13,19]，同时边坡越陡越容易发生破坏，也符合人们的认知常识[20-24]。在本文中有林边坡的安全系数均高于无林边坡，这也证明了青海云杉林根土复合体对边坡的稳定性确有提高作用，且这种提高作用随边坡坡度的增加呈指数函数增长（图3）。

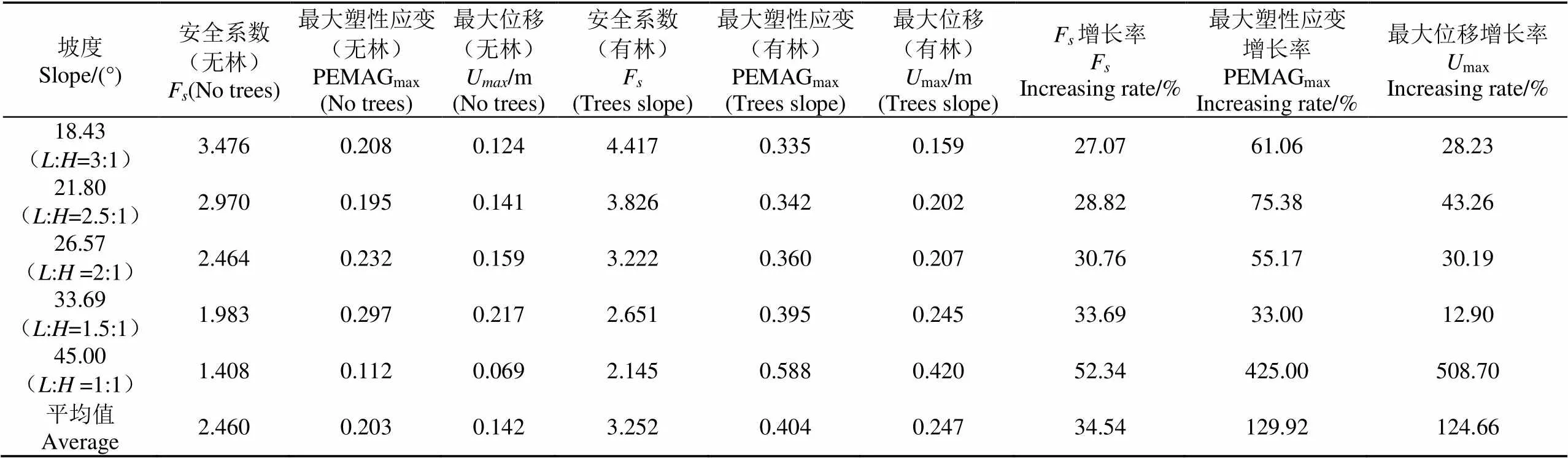
表4 不同坡度下的无林和有林（青海云杉）边坡参数及增长率

图3 边坡安全系数及增长率随坡度的变化规律

从图3反映的青海云杉林根土复合体提高边坡稳定性的规律看，边坡越陡根土复合体提高F的作用越强，这一现象在Chok等[11]的研究中也有所提及，其认为造成这种现象的主要原因是坡度越陡穿过土壤潜在破坏面的植物根系越多，因此对边坡安全系数提高的作用越大。

2.2.2 无林和有林边坡的PEMAGmax和max及其增长率随坡度的变化规律

图4是不同坡度下的PEMAGmax（最大塑性应变）和max（最大位移）的变化规律，从图4中可以看到，无林和有林边坡的PEMAGmax和max随坡度的变化规律有明显的不同。有林边坡的PEMAGmax，随坡度的增加而一直增大；而无林边坡的PEMAGmax起初随坡度的增加而增大，但是在坡度33.69°时出现了明显的拐点，拐点后的无林边坡PEMAGmax随坡度的增加而减小。有林与无林边坡的max随坡度的变化规律与PEMAGmax类似也是在坡度为33.69°出现拐点，拐点后的无林边坡max随坡度的增加而减小。PEMAGmax和max的这种变化规律说明：林地根土复合体的存在可以延长边坡的破坏时间，因为在同样的时间下，无林边坡的PEMAGmax和max可能已达到失稳的临界值，但是有林边坡由于根系的固土作用，PEMAGmax和max的值可以继续增大（图4－图5）[25-28]。因此，图5中可以明显看到，有林边坡的破坏时间t（注：本文采用数值计算不收敛作为判断边坡失稳的标准，这个不收敛的时间点定义为破坏时间t）均高于无林边坡，且破坏时间随着坡度的增加而减小，并呈指数函数递减（无林：=1.965 2e-0.041x，2=0.987 6；有林：=2.4692e-0.067x，2=0.995 6）。图5中青海云杉林根土复合体提高边坡破坏时间t的增长率随着坡度的增大呈抛物线增加（= 0.002 62-0.115 4+1.663 6，2=0.99）。这也说明了坡度越陡，根土复合体所发挥出的固坡作用越明显。

图4 最大塑性应变和最大位移及增长率随坡度的变化

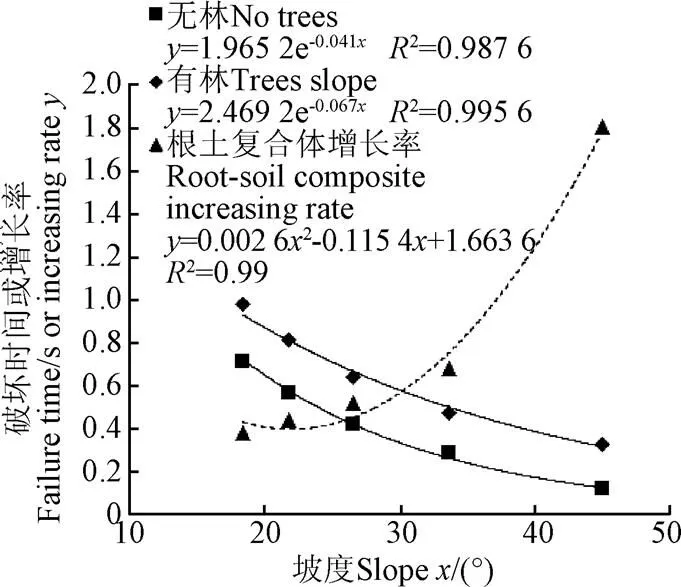
图5 破坏时间及增长率随坡度的变化

从表4和图4～6都可以看到，45°是一个值得注意的坡度。当边坡坡度达到45°时，无林边坡的PEMAGmax、max及t值都出现了较明显的降低，而PEMAGmax、max及t的增长率都有较明显的增加，这一现象要通过边坡破坏时的类型来解释。由图6可知，坡度为45°时无林边坡破坏时坡面并没有像其他坡度出现塑性贯通区，且PEMAGmax出现在坡顶位置。因此，45°无林边坡从边坡破坏类型上看并不属于滑坡（因为没有塑性滑动面），而是属于崩塌型的边坡破坏形式[15,29]。崩塌型破坏最主要的特点就是在坡顶由于张力的作用出现张裂缝并首先在坡顶发生破坏[30]，这与本文45°无林边坡的破坏特点完全一致。边坡破坏类型的不同，必然导致45°无林边坡PEMAGmax、max、t这3个值及其增长率出现较明显的变化。

2.2.3 影响边坡安全系数的因素分析（灰色关联度法）

本文通过变换土壤强度参数（、、）即摩擦角、黏聚力、剪胀角，来研究土壤强度参数对边坡稳定性的影响，从而找出导致边坡失稳的主要因素，当然坡度也是影响边坡稳定的主要因素，但是在上一节中已有所阐述，所以在灰色关联度分析中没有坡度参数。在本文中参数、、都有5个梯度，计算每个参数对应梯度下的边坡安全系数F，灰色关联度计算的原始数据如表5所示。利用式（3）～式（8）计算3个参数的灰色关联度γ矩阵和平均关联度Γ，结果见式（9）－式（13）。

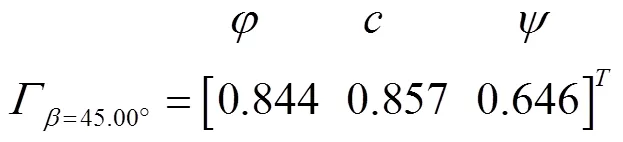
从式（9）～式（13）灰色关联度分析结果来看，在5个坡度下，φ、c、ψ，3个土壤强度参数与边坡安全系数Fs的关联顺序都为c>φ>ψ，也就是说坡度并不影响3个参数与Fs的关联顺序。可见，在本文中影响边坡安全系数的土壤强度因素中，黏聚力对安全系数的影响最大，摩擦角和剪胀角的影响次之。本文的参数研究参考了易绍基[17]和陈志波等[31]的灰色关联度分析法，易绍基[17]认为土壤本构模型如果选择Mohr-Coulomb（M-C）模型，则参数的敏感度排序为c>φ>ψ，如果采用Drucker-Prager（D-P）模型，参数的敏感度排序为c>ψ>φ，本文中土壤模型采用的M-C模型，研究结果与易绍基一致。但是，不管选取那种土壤本构模型，边坡安全系数对黏聚力的敏感度都是最高的。而根土复合体可以明显的增加土壤的黏聚力值，已被众多学者所证实[3-5,32-34]，因此这也是植被可以显著影响边坡稳定性的根本原因之一。

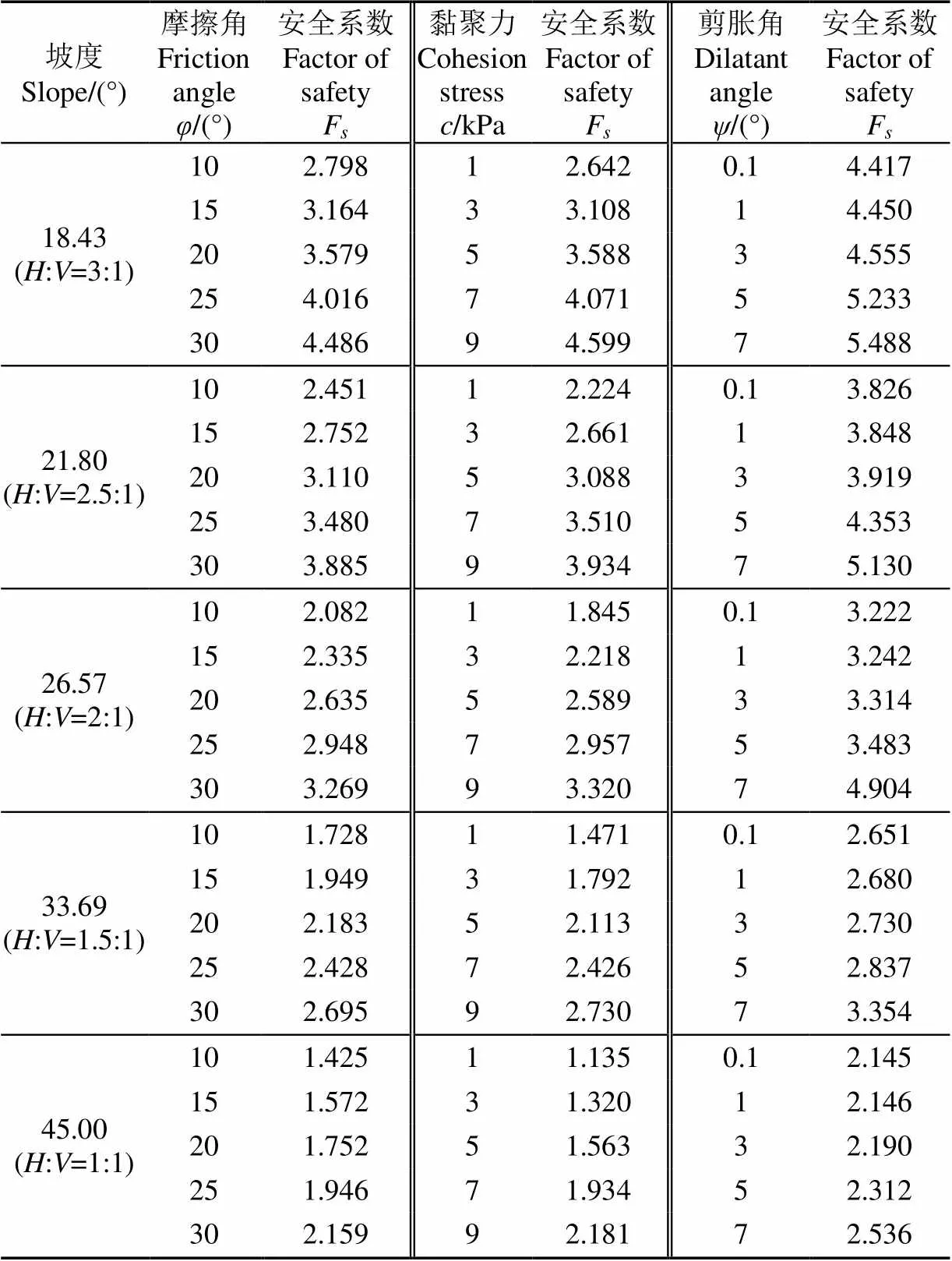
表5 土壤强度参数变化对青海云杉林边坡安全系数的影响

3 讨 论

3.1 边坡稳定性计算数值模型中的土壤参数

为了不改变土壤的物理性质和具有可比性，在本文中根土复合体和素土试样都是在野外获取的，而且是在同一次，同一天采样工作中获取的原状土。土壤参数试验中，作者利用三轴仪测定了根土复合体和素土的弹性模量，发现由于试样中根土复合体中的含根率最大不到1%（根系干质量/土壤干质量=根土复合体的含根率），导致两种土壤的弹性模量值并没有显著差别（图2）。同时作者也参阅了一些类似的研究文献[5,12-13]，发现其他学者在进行边坡稳定性数值模拟的时候，根土复合体和素土的弹性模量取值也是一样的（但是黏聚力、摩擦角是不一致的），这也印证了我们对弹性模量的试验结果。此外，弹性模量值一般都是MPa级别，青海云杉根土复合体和素土的弹性模量值在kPa或Pa级别的差别对结果规律的影响并不大。很多文献中都提到影响边坡稳定性的主要因素还是黏聚力、摩擦角、剪胀角这3个土壤强度参数[3,4,6,12,17,20]，因此本文选择这3个土壤强度参数研究它们对边坡安全系数的影响，而尽量减少其他因素对试验结果的影响。通过查阅文献一般土壤的泊松比都在0.3左右差别并不大[5,12,13,17,19]，更何况本文土壤试样都是来自同一地点，为此本文参考相关文献将土壤的泊松比设置为0.3。

3.2 根系增强边坡稳定性的作用机理（机械作用）

植物根系加固边坡的作用机理（机械作用）有3个方面：1）加筋作用，即将根系看作加筋材料，含根的土体看作加筋土，根系将约束限制土体的变形，提高土体的强度。根系的加筋作用可看作是为土体提供附加黏聚力[3]，从而使根土复合体的抗剪强度指标增加。2）锚固作用，土壤是不可以承受拉力的材料，但是土壤中的根系可以承受一定的拉力，当根土复合体受到边坡相对位移所产生的剪切力时，根土间就会发生错动，根系通过根土界面的摩擦作用，把土中的剪应力转化成为根的拉应力，从而增强了根土复合体的抗剪强度[35]。3）阻裂增延的作用，即阻止土体裂缝扩展，增加土体的延展性。土壤中的根系将土壤牢牢地包裹，形成一个整体。土体进入塑性状态后，由于摩擦作用土体中剪应力逐渐向根系转移并被扩散，而土体的应力、应变相对均匀，从而提高了根土复合体的抗裂性和延展性，进而增加了边坡的稳定性[36]。上述有关植物根系加固边坡的力学机制主要建立在土的莫库仑强度理论上，即当土壤强度参数、值增加，则其抗剪强度将增加。

3.3 根土复合体影响边坡稳定性的因素

由于植物的存在影响了土壤的结构，从而影响了林地土壤的强度参数，导致了边坡稳定性的变化。导致这一变化的内因十分复杂，除了根土之间的相互作用（机械作用）外，还有植物产生的水文效应（如蒸腾作用、林冠截流、吸水降压等）[3,5,21]；也有植物产生的生物作用（如根系的分泌物、形态、粗糙度等）都会改变土壤结构[21]，所以根系加固边坡的内因十分复杂，很难用简单和单一手段来研究。但是，土壤的强度参数变化（黏聚力、摩擦角等）正是这些复杂内因的外在综合表现。所以国内外对植物稳定边坡作用的数值模拟研究大部分也都是以土壤参数变换、地形参数变换（如坡度）、降雨条件参数变换（如雨强、历时）对边坡稳定性的影响为主要研究内容[5,6,11,13,29-30]。这种研究方法可以综合反映出植物对土壤结构的物理、化学、水文等影响，试验结果也更符合实际。因此，本文选择通过土壤强度参数的变换，分析影响青海云杉边坡稳定性的因素，体现青海云杉在贺兰山水土保持中的重要生态价值。

4 结 论

本文通过建立不同坡度下的贺兰山青海云杉林边坡稳定性计算有限元模型，计算了不同坡度下有林和无林边坡的安全系数、最大塑性应变、最大位移、破坏时间及它们的增长率随边坡坡度的变化规律，并计算了土壤强度参数与边坡安全系数的灰色关联度，经过分析讨论可以得出以下结论：

1）无林边坡与有林边坡的安全系数随坡度的变化规律是一致的，都以幂函数递减，无林：=65.089-1.001（2= 0.996 7）；有林：=46.775-0.813（2=0.998 7）。有林边坡相对于无林边坡安全系数的增长率以指数函数增加：=1.6704e0.0239x（2=0.933 9），且边坡坡度越陡根土复合体对边坡稳定性的提高作用越强。

2）根土复合体的存在可以延长边坡的破坏时间，有林边坡的破坏时间均高于无林边坡，根土复合体提高边坡破坏时间的增长率随坡度的增大呈抛物线增加：= 0.00262-0.115 4+1.663 6（2=0.99），且坡度越陡提高作用越明显。边坡破坏时有无塑性贯通区会明显改变最大塑性应变、最大位移、破坏时间的值。

3）黏聚力、摩擦角、剪胀角3个土壤强度参数中，黏聚力是影响边坡稳定的主导因素，摩擦角、剪胀角的影响次之，此规律不受边坡坡度的影响。植物根系提高了边坡土壤的黏聚力，这是根土复合体可以显著影响边坡稳定性的根本原因之一。

[1] 杨淑萍，孙银川，尤志宇，等. 宁夏地质灾害气象条件的初步研究[J]. 新疆气象，2005，28(6)：7－10.

Yang Shuping, Sun Yinchuan, You Zhiyu, et al. A preliminary study of Ningxia on meteorological conditions geological disasters[J]. Bimonthly of Xinjiang Meteorology, 2005, 28(6): 7－10. (in Chinese with English abstract)

[2] 赵晓春，刘建军，任军辉，等. 贺兰山4种典型森林类型凋落物持水性能研究[J]. 水土保持研究，2011，18(2)：107－111.

Zhao Xiaochun, Liu Jianjun, Ren Junhui, et al. Study on water-holding capacity of litter in four forest types of Helan Mountain[J]. Research of Soil and Water Conservation, 2011, 18(2): 107－111. (in Chinese with English abstract)

[3] 田佳，曹兵，及金楠，等. 花棒根-土复合体直剪试验的有限元数值模拟与验证[J]. 农业工程学报，2015，31(16)：152－158.

Tian Jia, Cao Bing, Ji Jinnan, et al. Numerical simulation of direct shear test for root-soil composite ofusing a finite element method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(16): 152－158. (in Chinese with English abstract)

[4] 及金楠，张志强，郭军庭，等. 黄土高原刺槐和侧柏根系固坡的有限元数值模拟[J]. 农业工程学报，2014，30(19)：146－154.

Ji Jinnan, Zhang Zhiqiang, Guo Junting, et al. Finite element numerical simulation of Black Locust () and Arborvitae () roots on slope stability on Loess Plateau of China[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(19): 146－154. (in Chinese with English abstract)

[5] Lin Der Guey, Huang Bor Shun, Lin Shin-Hwei. 3-D numerical investigations into the shear strength of the soil-root system of Makino bamboo and its effect on slope stability[J]. Ecological Engineering, 2010, 36(8): 992－1006.

[6] Mickovski S B, Stokes A, van Beek, et al. Simulation of direct shear tests on rooted and non-rooted soil using finite element analysis[J]. Ecological Engineering, 2011, 37(10): 1523－1532.

[7] Mao Zhun, Yang Ming, Bourrier F, et al. Evaluation of root reinforcement models using numerical modeling approaches[J]. Plant Soil, 2014, 381(1/2): 249－270.

[8] Bourrier F, Kneib F, Chareyre B, et al. Discrete modeling of granular soils reinforcement by plant roots[J]. Ecological Engineering, 2013, 61(Part C): 646－657.

[9] Ji Jinnan, Kokutse N, Genet M, et al. Effect of spatial variation of tree root characteristics on slope stability. A case study on Black Locust () and Arborvitae () stands on the Loess Plateau, China[J]. Catena, 2012, 92(5): 139－15.

[10] 魏晓，孙峰华. 宁夏水土保持及区划研究[J]. 水土保持研究，2005，12(6)：119－121.

Wei Xiao, Sun Fenghua. Study on soil and water conservation of Ningxia and it’s Division[J]. Research of Soil and Water Conservation, 2005, 12(6): 119－121. (in Chinese with English abstract)

[11] Chok Y H, Jaksa M B, Kaggwa W S, et al. Assessing the influence of root reinforcement on slope stability by finite elements[J]. Geo-Engineering, 2015, 6(12): 1－13.

[12] Dupuy L, Fourcaud T, Lac P, et al. A generic 3D finite element model of tree anchorage integrating soil mechanics and real root system architecture[J]. American Journal of Botany, 2007, 94(9): 1506－1514.

[13] Fan C C, Lai Y F. Influence of the spatial layout of vegetation on the stability of slopes[J]. Plant Soil, 2014, 377(1): 83－95.

[14] 中华人民共和国水利部. 土工试验方法标准：GB/T50123-1999[S]. 北京：中国计划出版社，1999：110－114.

[15] Schwarz M, Rist A, Cohen D, et al. Root reinforcement of soils under compression[J]. Journal of Geophysical Research: Earth Surface, 2015, 120(10): 2103－2120.

[16] 费康，张建伟. ABAQUS在岩土工程中的应用[M]. 北京：中国水利出版社，2010.

[17] 易绍基. 基于ABAQUS的边坡稳定敏感性分析及模型验证[D]. 昆明：昆明理工大学，2011.

Yi Shaoji. Sensitivity Analysis and Model Verification of Slope Stability Based on ABAQUS[D]. Kunming: Kunming University of Science and Technology, 2011. (in Chinese with English abstract)

[18] 谢仁海，渠天祥，钱光谟，等. 构造地质学[M]. 北京：中国矿业大学出版社，2007.

[19] Mao Zhun, Bourrier F, Stokes A, et al. Three-dimensional modelling of slope stability in heterogeneous montane forest ecosystems[J]. Ecological Modelling, 2014, 273(2): 1－22.

[20] Duckett N. Development of Improved Predictive Tools for Mechanical Soil Root Interaction[D]. Dundee: University of Dundee, 2013.

[21] Stokes A, Douglas B G, Fourcaud T. Ecological mitigation of hillslope instability: Ten key issues facing researchers and practitioners[J]. Plant Soil, 2014, 377(1/2): 1－23.

[22] Yang M, Défossez P, Danjon F, et al. Tree stability under wind: Simulating uprooting with root breakage using a finite element method[J]. Annals of Botany, 2014, 114(4): 695－709.

[23] Tardio G, Mickovski S B . Method for synchronisation of soil and root behaviour for assessment of stability of vegetated slopes[J]. Ecological Engineering, 2015, 82(1): 222－230.

[24] Fourcaud T, Ji J N, Zhang Z Q, et al. Understanding the impact of root morphology on overturning mechanisms: A modelling approach[J]. Annals of Botany, 2008, 101(8): 1267－1280.

[25] Kokutse N K, Temgoua A G, Kavazovic Z, et al. Slope stability and vegetation: Conceptual and numerical investigation of mechanical effects[J]. Ecological Engineering, 2016, 101(1): 146－153.

[26] Prasad A, Kazemian S, Kalantari B, et al. Stability of tropical residual soil slope reinforced by live pole: Experimental and numerical Investigations[J].Arabian Journal for Science and Engineering, 2012, 37(3): 601－618.

[27] Khalilnejad A, Ali F, Hashim R, et al. Finite-element simulation for contribution of matric suction and friction angle to stress distribution during pulling-out process[J]. International Journal of Geomechanics, 2013, 13(5): 527－532.

[28] Karami1 A, Stead D. Asperity degradation and damage in the direct shear test: A hybrid FEM/DEM approach[J].Rock Mechanics and Rock Engineering, 2008, 41(2): 229－266.

[29] Temgoua A G T, Kokutse N K, Kavazović Z. Influence of forest stands and root morphologies on hillslope stability[J]. Ecological Engineering, 2016, 95(1): 622－634.

[30] Chinkulkijniwat A, Yubonchit S, Horpibulsuk S, et al. Hydrological responses and stability analysis of shallow slopes with cohesionless soil subjected to continuous rainfall[J]. Canada Geotech Journal, 2016, 53(12): 2001－2013.

[31] 陈志波，简文. 边坡稳定性影响因素敏感性灰色关联分析[J]. 防灾减灾工程学报，2006，26(4)：473－477.

Chen Zhibo, Jian Wen. Sensibility analysis of slopes stability based on gray correlation analysis[J]. Journal of Disaster Prevention and Mitigation Engineering, 2006, 26(4):473－477.

[32] Bahaaddini M, Sharrock G, Hebblewhite B K. Numerical direct shear tests to model the shear behaviour of rock joints[J]. Computers and Geotechnics, 2013, 51(6): 101－115.

[33] Pollen Bankhead N, Simon A, Thomas R E. The reinforcement of soil by roots: Recent advances and directions for future research[J]. Treatise on Geomorphology, 2013, 12(3): 103－127.

[34] 陈丽华，刘秀萍，宋维峰，等. 刺槐林边坡稳定性有限元分析[J]. 北京林业大学学报，2008， 30(增刊2)：206－210.

Chen Lihua, Liu Xiuping, Song Weifeng, et al. Finite element analysis offorest slope stability[J]. Journal of Beijing Forestry University, 2008, 30(Supp.2): 206－210. (in Chinese with English abstract)

[35] 田佳，曹兵，及金楠，等. 花棒、沙柳根系生物力学特性研究[J]. 农业工程学报，2014，30(23)：192－198.

Tian Jia, Cao Bing, Ji Jinnan, et al. Biomechanical characteristics of root systems of Hedysarum scoparium and Salix psammophila[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(23): 192－198. (in Chinese with English abstract)

[36] 周云艳，陈建平，王晓梅. 植物根系固土护坡机理的研究进展及展望[J]. 生态环境学报，2012，21(6)：1171－1177.

Zhou Yunyan, Chen Jianping, Wang Xiaomei. Progress of study on soil reinforcement mechanisms by root and its expectation[J]. Ecology and Environmental Sciences, 2012, 21(6): 1171－1177. (in Chinese with English abstract)

Analysis on improvement of slope stability in root-soil composite offorest in Helan Mountain

Tian Jia1, Ji Jinnan2, Zhong Qi1, Yu Pengcheng1, Yang Lijiao1, Yuan Bo1

(1.,750021; 2.100083,)

Helan Mountain is an area prone to geological hazard and an ecological shelter in Yinchuan Plain. Plants have been widely used for controlling shallow landslides and soil and water loss in this area. The exact study site is located at the Tu’erkeng forest protection point in Suyukou national forest park. To reveal mechanisms of slope stability reinforced by root-soil composite, we built a finite element numerical model to simulate the impact of root-soil composite on slope stability. Picea crassifolia was selected as research object, which is one of the most important trees for soil and water conservation in Helan Moutain. In this paper, direct shear tests and triaxial tests of root-soil composite and pure soil were conducted for getting soil strength parameters, and based on the soil parameters, the finite element numerical model for the stability calculation of Picea crassifolia forest slope was established. All the soils, including the root-soil composite and the plain soil, were undisturbed samples and were obtained from the same time and field. In the numerical model, the soil was defined as ideal elastoplastic material and following the Mohr-Coulomb yield criterion. The soil and rock were divided by triangular elements of plane strain (CPE6MP and CPE3). Using the model, factor of safety, maximum plastic strain, maximum displacement, failure time, and their growth rate with the slope grade (18.43°, 21.80°, 26.57°, 33.69° and 45.00°) were studied. In this paper we also calculated the grey relational coefficient between the factor of safety and soil strength parameters including friction angle, cohesion, and dilation angle. It was found that: 1) The relationships between factor of safety and slope grade are similar in the slopes with or without trees, and they all decrease in power function. The growth rate of factor of safety increases with the increasing of the slope grade and shows the exponential change. The steeper the slope, the stronger root-soil composite improves the slope stability. 2) The existence of the root-soil composite can prolong the failure time of the slope, and the failure time of the slope with trees is longer than that without trees. The growth rate of the slope failure time increases with the increasing of the slope grade, showing a parabolic curve, and the steeper the slope, the more obvious the effect. With or without plastic-perforation zone, the maximum plastic strain, maximum displacement and failure time of the slope will have an obvious difference. 3) In the 3 soil strength parameters, the cohesion has the greatest influence on the slope stability. The next is the friction angle and the dilation angle. Moreover, this order is not affected by the slope grade. This is also one of the fundamental reasons why vegetation can affect slope stability obviously. The successful implement of this research can play a key role in understanding the nature of root-soil composite reinforcement, promoting numerical simulation study on slope stability and preventing shallow landslides and soil and water losses in Helan Mountain.

slope stability; soils; numerical simulation; root-soil composite; Helan Mountain;

10.11975/j.issn.1002-6819.2017.20.018

S157.2

A

1002-6819(2017)-20-0144-09

2017-05-22

2017-10-18

国家自然科学基金资助项目（31560232；31400616）

田 佳，副教授，博士，主要从事水土保持与荒漠化防治研究。Email：yuhudie63@qq.com

田 佳，及金楠，钟 琦，余鹏程，杨丽娇，袁 博. 贺兰山云杉林根土复合体提高边坡稳定性分析[J]. 农业工程学报，2017，33(20)：144－152. doi：10.11975/j.issn.1002-6819.2017.20.018 http://www.tcsae.org

Tian Jia, Ji Jinnan, Zhong Qi, Yu Pengcheng, Yang Lijiao, Yuan Bo. Analysis on improvement of slope stability in root-soil composite offorest in Helan Mountain[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(20): 144－152. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.20.018 http://www.tcsae.org