非周期波浪与直墙作用的非线性数值研究1)

李 翔 张崇伟 宁德志 苏 朋

(大连理工大学海岸和近海国家重点实验室，大连116024)

非周期波浪与直墙作用的非线性数值研究1)

李 翔 张崇伟 宁德志2)苏 朋

(大连理工大学海岸和近海国家重点实验室，大连116024)

基于时域高阶边界元方法，建立了完全非线性二维数值波浪水槽，对非周期波浪与直墙的相互作用问题进行了模拟和研究.自由表面满足完全非线性自由水面运动学和动力学边界条件，采用混合欧拉--拉格朗日方法追踪瞬时自由面流体质点，采用四阶Runge-Kutta法对下一时间步的波面和自由面速度势进行更新.采用加速度式法求解直墙表面速度势的时间导数，对瞬时物体湿表面上的水动力压强积分,得到作用在物体上的瞬时波浪力.首先,将全非线性与Serre-Green-Naghdi(SGN)模型的结果进行了对比分析，发现对于大幅值双入射波问题，仅满足弱色散关系的SGN模型大大低估了最大波浪爬高;其次，研究了双入射波与直墙的非线性作用问题，发现线性预报对波浪最大爬高有较大低估，而波浪的非线性成分不只导致了自由面爬高的异常增大，也引起了局部自由面的高频振荡,该物理过程中，直墙所受的波浪载荷，也展示出了与波浪爬高相似的非线性特性;最后,对波浪爬升和波浪力的时间历程进行了频谱分析，发现入射主频波的部分能量传递给了更高频的波浪成分，反映出该问题具有典型的非线性特性.

非线性波浪，波浪爬高，时域模拟，高阶边界元，GN理论

引言

近年来，由于大型海洋结构的广泛应用，波浪与海洋结构相互作用的问题越来越被人们所重视，并在近年来得到了广泛的研究[13].其中，直墙式结构是一种常见的海岸工程结构，其安全性和造价很大程度上取决于作用在其上的极限波浪载荷.工程实际中，人们多通过研究波浪沿直墙的爬高，来预报该极限波浪载荷.

针对波浪爬高问题，目前人们围绕连续波浪、孤立波与直墙的相互作用已经做了大量研究.例如，对于连续波，Isaacson和Cheung[4]提出了二阶时域模拟的理论模型，研究了波浪在直壁物体上的爬高问题.Grilli等[5]基于全非线性势流理论，建立了三维数值水槽，利用边界元方法来模拟波浪爬高.Jamois等[6]使用基于高阶Boussinesq方程的有限差分模型，对三维波浪在竖直板的爬高问题进行了研究.Fuhrman和Madsen[7]在高阶Boussinesq模型中引入了一种插值技术来捕捉非线性自由面沿壁面的爬高.Pelinovsky等[8]求解了直墙附近非线性浅水方程，并给出了直墙附近出现畸形波的概率分布.孙英伟[9]以Naiver-Stokes方程为基本控制方程，采用流体体积和大涡模拟方法，研究了规则波作用于直墙过程中的流场形态和波浪力.Chatjigeorgiou和Molin[10]采用了改进型Boussinesq方程来研究波浪与直墙的相互作用问题，发现波浪爬升与入射波和反射波的三阶非线性作用密切相关.

对于孤立波，Su和 Mirie[11]通过摄动展开法推导了孤立波沿直墙爬高的三阶解析解.Fenton和Rienecker[12]采用谱方法研究了孤立波在直墙上的碰撞问题，发现该过程对反射波的波高和波速都产生了影响，而考虑三阶非线性效应的模拟结果可准确预测最大波浪爬高，但无法准确预测反射波相位的改变.Kim等[13]最早使用二维边界元方法，模拟了考虑完全非线性自由面条件的孤立波沿直墙的爬高问题.Power和Chwang[14]对孤立波的直墙反射问题，给出了Boussinesq方程的解析解和数值解，也发现了反射孤立波的相位延迟现象.Cooker等[15]使用二维时域全非线性边界元方法研究了大幅孤立波与直墙相互作用，发现孤立波碰撞直墙后能量耗散给一群色散波，降低了反射波波高和波速;同时，直墙上波浪下降要比其爬升过程消耗更多时间.Maiti和Sen[16]采用时域全非线性边界元方法分析了孤立波与直墙非线性作用问题，他们发现，比起倾斜墙壁，垂直墙壁上波浪作用的非线性效应更显著.Liu和Al-Banaa[17]对孤立波在下方有开孔的直墙上的爬高进行了物理模型实验.Jian等[18]采用光滑粒子水动力学方法，对包含波浪破碎过程的孤立波爬高问题进行了模拟.Park和Cox[19]建立了近岸波浪和风暴潮爬高的经验公式.Chambarel等[20]采用考虑全非线性自由表面的二维边界元方法模拟了两相同孤立波的对撞问题(等效于孤立波与直墙的对撞问题)，观测到了射流现象.宣瑞韬等[21]通过物理试验研究了双孤立波的直墙爬高问题，着重分析了两波相对波高和波距对波浪爬高的影响.

近期Carbone等[22]指出，某些特殊波浪(如非周期波浪)也值得关注.非周期波浪与直墙作用时可能会产生比连续波浪更大的波浪爬高，导致更大的波浪载荷，从而威胁结构的安全性.为了提高计算效率，他们在数值模拟中采用了基于浅水假设且仅满足弱色散关系的Serre-Green-Naghdi(SGN)[2326]波浪模型.而Cooker等[12]提出波浪爬高问题会伴随一群色散波.因此，本文将基于全非线性势流模型，进一步对文献[19]中涉及到的非周期波浪与直墙相互作用的问题进行研究，通过与SGN模型结果的对比，研究SGN模型在该问题中的适用性.另外，本文将重点研究直墙结构上双入射波爬升和载荷的非线性特性.通过频谱分析，研究波浪爬升过程中各频率组分的能量分布，进而分析波与波相互作用的非线性物理特征.

1 数学模型

本文将建立如图1所示的二维数值波浪水槽.水槽左侧为造波推板，右侧为直墙.水槽长度为L，平均水深为d，造波板、自由水面、直墙和水底边界分别用Γw,Γf,Γb,Γd来表示，流域用V来表示.

图1 波浪水槽示意图Fig.1 Sketch of the wave fl ume

建立笛卡尔坐标系oxz，其中o位于造波板与自由水面平均位置的交点处，ox指向右侧水平方向，oz竖直向上.假定流体为理想流体且其运动无旋，则可采用势流理论模型来描述水槽内水体运动，并得到下述初边值问题

其中，速度势ϕ(x,y,z)为标量，其空间梯度为流体的速度，η表示自由面波高，g为重力加速度，∂ϕ/∂n表示速度势在物面法线方向的偏导数.造波板的速度u(t)设为

式中，a和ω分别为波浪的幅值和频率，T为波浪周期，H(t)为Heaviside函数

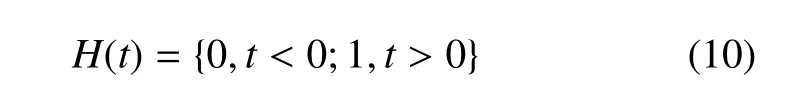
作用在直墙上的水平波浪力可通过对Bernoulli方程得到的压力进行积分求得

式中ϕt为速度势对时间的偏导数.可通过求解下列边值问题得到

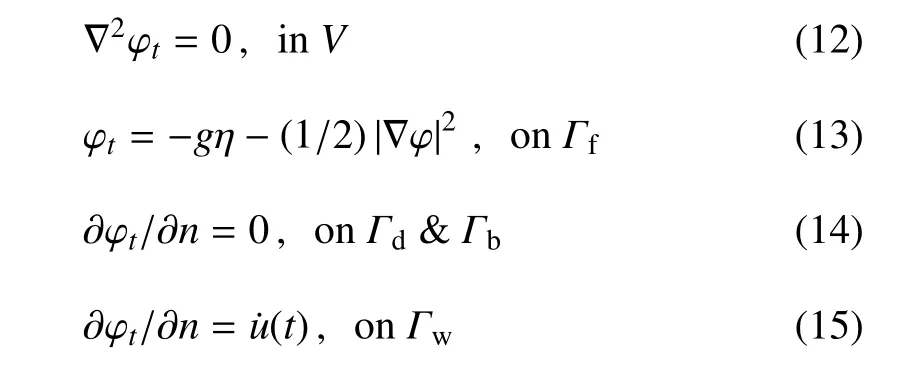
2 数值方法

根据格林第二定理，方程(1)可转换为下述边界积分方程[27]

式中，p={x0,z0}为配置点坐标，q={x,z}为边界上一点的坐标，C为固角系数[27]，Γ为全部流域边界，G为简单格林函数.对于该二维问题，G(p,q)可定义为

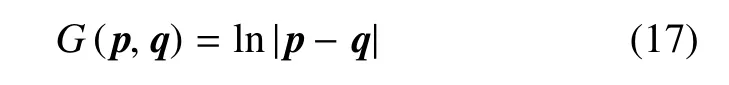
进一步采用边界单元来离散流域边界.为了更准确地描述流域边界，这里采用曲线单元，即用二次曲线来逼近真实的几何边界，它比直线单元具有更强的适应性.单元上任一点的坐标和速度势等物理量可通过如下插值得到

式中，M为单元上节点个数，S用来表示x，z，φ和∂φ/∂n等物理量，Sn为单元上第n个节点处物理量的值，ξ∈[−1.0,1.0]为固有坐标，hn表示第n个形状函数

这里采用三节点二次高阶单元来离散流域边界，即M=3.该方法比常数单元和线性单元具有更高的精度.

式中，d(e,m)表示第e个单元上第 m个节点的编号，Ne为边界单元的数量.J(ξ)是雅可比(Jacobian)行列式，可写为如下形式

积分方程经过离散后，可通过求解线性方程组得到未知量.

在每一个时间步，自由面上的速度势和其他物面上的速度势法向导数是已知的，通过求解线性方程组(20)，可以得到物面上速度势和自由面上速度势法向导数的值.通过差分可以得到边界上速度势的切向导数，并通过下列关系求得速度势的空间导数值

其中，n={nx,nz}为单位法向量.

根据自由面边界条件，可得到速度势和波高的时间偏导数，可应用数值积分的方法，进行时间步进，计算得到下一时刻自由面上的速度势和波高.本文选用四阶Runge-Kutta法对自由面条件进行时间积分.为了叙述方便，将自由面边界条件写成如下常微分方程的形式

则t+∆t时刻波面高度η(t+∆t)和速度势ϕ(t+∆t)可写为

其中

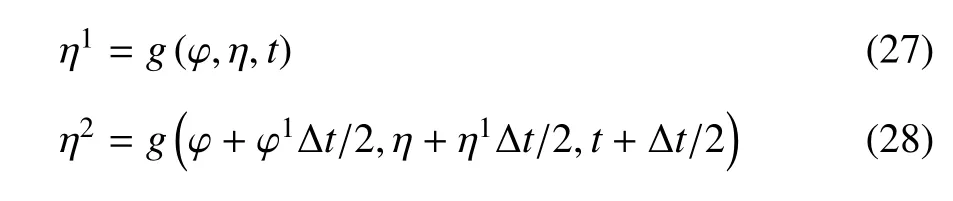
3 计算结果及分析

下面，我们将利用前面建立的数值波浪水槽，研究不连续波对直墙的作用.在本文中，以d,g和ρ作为无量纲基准，其他参数均为无量纲数.为防止反射波在造波板处发生二次反射，对计算域长度和模拟时间进行如下控制

其中，Nw为非周期波浪数，λ为入射波波长.

在本文的数值模拟中，设置自由面上单元的长度为∆x=λ/600，水深方向布置10个单元，时间步长取∆t=T/200.该模型的收敛性和精度等已在此前的工作[28]中得到验证，故此处不再赘述.

3.1 单入射波作用的情况

首先考虑单个入射波(Nw=1)的情况.为与文献[19]中的SGN模型结果进行对比，设定入射波的频率为ω0=0.145，幅值为a=0.05.图2给出了直墙处自由面爬升的时间历程.本文数值模拟结果与文献[19]中的SGN模型的结果非常吻合，验证了本模型计算结果的可靠性.图3显示了自由面沿直墙爬高达到最大值时(t=1.67T)的自由表面形状，本文的模拟结果同样与SGN模型的结果相吻合.

图4进一步测试了不同入射频率下单入射波沿直墙的最大波浪爬高R，本模型结果和SGN模型结果吻合得依然很好.从图中可以看出，低频入射波的最大波浪爬高约是入射波波幅的2倍，接近线性波浪理论的预测结果.而频率在ω0附近的单入射波可产生达到2.3倍入射波波高的自由面爬高，表现出了明显的非线性特征.

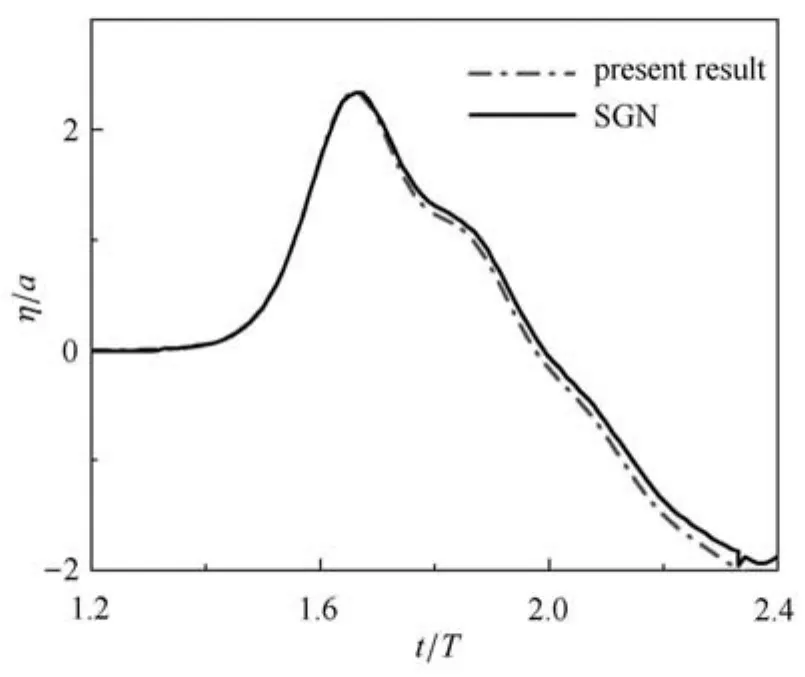
图2 单入射波在直墙上爬高的时间历程Fig.2 History of wave run-up along the vertical wall for the single incident wave

图3 单入射波在t=1.67T时刻的波面形状Fig.3 Free surface pro fi le at t=1.67T for the single incident wave

图4 不同频率的单入射波沿直墙的最大爬高Fig.4 Maximum wave run-up along the vertical wall for single incident wave of di ff erent frequencies

3.2 双入射波作用的情况

接下来考虑双入射波(Nw=2)的情况.入射波频率设为ω0=0.02.图5给出了不同波幅(a=0.048,a=0.049和 a=0.05)的双入射波撞击直墙后，自由面沿直墙爬升的时间历程.与单入射波的情况相比，双入射波的两个波峰撞击直墙时，自由面爬高均显示出高频振荡的特征.该高频振荡在直墙反射波与第二个入射波相遇时尤为明显.通过与SGN模型结果的对比，可以发现入射波波幅较小时(即a=0.048)，本模型结果与SGN模型的结果有很好的吻合.随着入射波波幅的增大，本文与SGN模型的结果，在第一个入射波爬高、回落和第二个入射波回落阶段，比较吻合;但在第二个入射波的爬高阶段，二者的差别随入射波波高的增大而增大.对于幅值为a=0.05的入射波，本文模型得到的最大波浪爬高可达到4.4倍入射波波高，而SGN模型预报的最大爬高为入射波波高的3.8倍.同时，本文波浪爬高历程的震荡也更加剧烈.

图5 不同波幅下双入射波直墙上爬高的时间历程Fig.5 History of wave run-up along the vertical wall for double incident waves with di ff erent amplitudes

本文进一步考虑了其他频率的情况.图6给出了不同入射波频率下双入射波沿直墙的最大爬高.从图中可以看出，随着入射波波幅的增大，本文模型得到的最大波浪爬高越来越高于SGN模型的预报值.对于幅值为a=0.05的入射波，两个模型结果的差别随频率的增大而逐渐减小，并最终趋于稳定.本文的非线性数值结果显示，波浪沿直壁的最大爬高可达到5倍入射波幅，大于SGN模型预报的3.8倍入射波幅.非线性结果中激发最大波浪爬高的入射波的频率，则略小于SGN结果中最大爬高对应的入射波频率.在图6中可以发现，入射波频率越小，两种模型的差别越大，说明波浪频率越低，产生的非线性越强.

图6 不同波幅下不同频率的双入射波沿直墙的最大爬高Fig.6 Maximum wave run-up along the vertical wall for double incident waves of di ff erent frequencies and amplitudes

由于SGN模型是基于浅水假设且仅满足弱色散关系，而本文所采用的完全非线性模型并不受SGN模型假设的限制，因此有理由相信本文模型能更准确地反映本文所涉及的非线性问题.进一步联系到3.1节单入射波的情况，可以得知SGN模型可对单个非线性入射波进行准确模拟，而对于双入射波情况下的非线性波与波相互作用，SGN模型的模拟精度是有限的，其结果低估了可能的最大波浪爬高.

3.3 双入射波作用的非线性分析

下面将基于本文模型，对幅值为a=0.05的双入射波与直墙相互作用的非线性特性做更进一步研究.图7给出了不同频率(ω=0.02，ω=0.1和ω=0.2)的双入射波撞击直墙后，自由面沿直墙爬升的时间历程.其中，线性结果可通过将非线性自由面条件(方程(2)和方程(3))线性化得到的.图中各非线性结果明显不同于相应的线性结果.一方面，波浪的非线性成分导致了自由面爬高的异常增大，使得线性预报明显低估了波浪的最大爬高.另一方面，在第二个波浪的爬升阶段，非线性结果显示出大幅的高频振荡，该振荡的频率随着入射波频率的增加而减小.这反映出，随着入射波频率的增大，第二个波与前一个波的反射波发生相互作用的非线性效应在减弱，同时也导致其最大爬高减小.

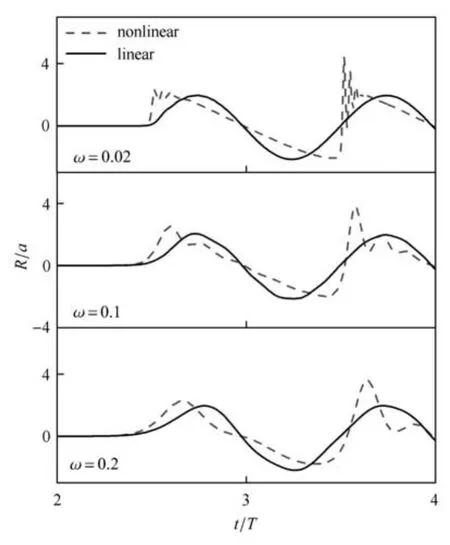
图7 不同频率的双入射波在直墙上爬高的时间历程Fig.7 History of wave run-up along the vertical wall for double incident waves of di ff erent wave frequencies

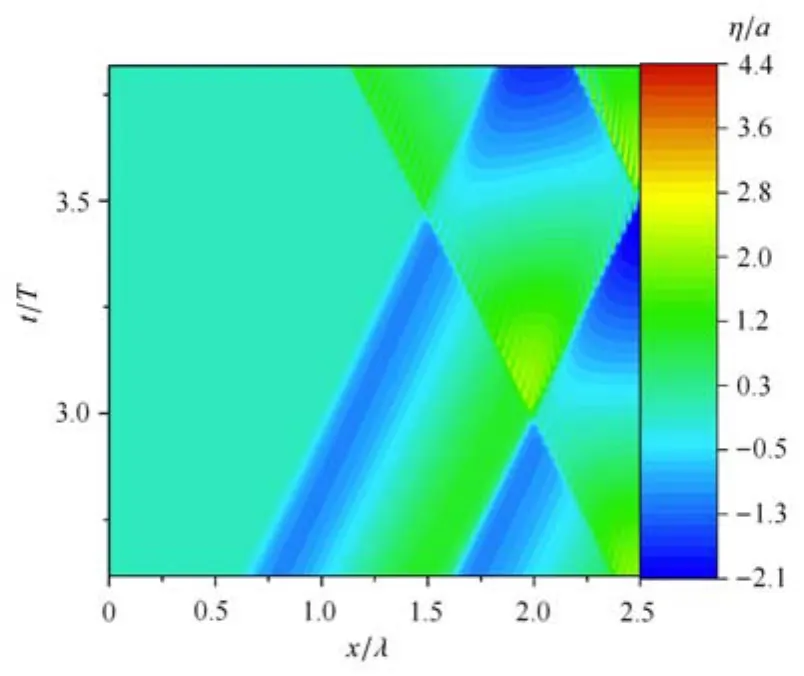
图8 双入射波波形的时间历程Fig.8 Evolution of wave pro fi les for double incident waves

图8给出了数值水槽内频率为ω=0.02的双入射波的波形随时间的变化.从图中可以看出，波浪与直墙的作用过程可分为撞击前、撞击中、撞击后三个阶段.第二个波与第一个波的反射波相遇时，汇合成一个波峰，其幅值在极短的时间内迅速增大至约两倍于入射波波高.随后两波分离，继续沿各自来向传播.在该过程中，两波之间的水面形成了一系列的振荡波.随后，与第一个波的反射波作用之后的第二个入射波碰撞直墙，开始了爬高过程，其波高的高频振荡也在直墙上检测到，此时在直墙上波浪的最大爬高远大于入射波波幅的二倍.

图9进一步给出了各频率的双入射波作用于直墙的波浪力的时间历程.其展示出来的非线性特性与波浪爬高过程基本相同.

图9 不同频率的双入射波对直墙作用力的时间历程Fig.9 History of wave force acting on the vertical wall for double incident waves of di ff erent wave frequencies

图10给出了不同频率的双入射波，沿直墙的最大爬高和对直墙的最大波浪力，其中设ω0=0.02.从图中可以看出，最大波浪爬高和最大波浪力随入射波频率的变化趋势基本相同，其峰值都出现在略低于ω0的频率处.峰值处最大波浪爬高可高达约为5倍的入射波高，而最大波浪力可达到2.5倍线性预报值.对于ω＞ω0，非线性波浪爬高和波浪力的最大值逐渐减小，但始终大于线性预报值.

图10 不同频率的双入射波沿直墙的最大爬高和对直墙的最大波浪力Fig.10 Maximum wave run-up along the vertical wall and maximum wave force acting on the vertical wall for double incident waves of di ff erent wave frequencies

图11进一步对图 7和图9中ω0=0.02时的波浪爬升和波浪力时间历程进行了频谱分析.频率为ω=ω0的组分在线性和非线性结果中均占主导地位.而相较于线性结果，非线性结果在ω=2ω0,ω=3ω0,ω=4ω0等入射频率整数倍的高频处也均出现不可忽略的峰值.这反映了，在入射波与反射波相互作用的过程中，由于波浪的非线性特性，不同频率的波浪发生了能量交换，入射主频波的能量传递给了更高频的波浪成分.该现象表明双入射波沿直墙爬高问题有典型的非线性特性.

图11 双入射波沿直墙爬高和对直墙作用力的频谱Fig.11 Spectra of wave run-up and force on vertical wall for double incident waves

4 结论

本文基于时域高阶边界元方法，建立了完全非线性二维数值波浪水槽模型，对非周期波浪与直墙的相互作用问题进行了模拟和研究.

本文首先将全非线性的结果与SGN模型的结果进行了对比分析.对于单入射波撞击直墙的情况，全非线性结果与SGN模型的结果非常吻合.而对于非线性效应更高的大幅值双入射波问题，仅满足弱色散关系的SGN模型的模拟结果大大低估了最大波浪爬高.尤其在第二个入射波撞击直墙时，全非线性方法模拟的波面爬高显示出了更剧烈的振荡特征.

本文更进一步研究了大幅值双入射波与直墙的作用问题，确认了该问题的强非线性特性.发现线性预报对波浪最大爬高有较大低估，而波浪的非线性成分不只导致了自由面爬高的异常增大，也引起了局部自由面的高频振荡，而该振荡的频率随着入射波频率的增加而减小.该物理过程中，双入射波作用于直墙的波浪载荷，也展示出了与波浪爬高相似的非线性特性.

最后，本文对波浪爬升和波浪力的时间历程进行了频谱分析.结果显示，由于入射波与反射波的非线性作用，入射主频波的部分能量传递给了更高频的波浪成分，体现出了典型的非线性特性.

1张新曙,胡晓峰,尤云祥等.深海多立柱浮式平台涡激运动特性研究.力学学报,2016,48(3):593-598(Zhang Xinshu,Hu Xiaofeng,You Yunxiang,et al.Investigation on the characteristics of vortex induced motion of a deep sea muti-column fl oating platform.Chinese Journal of Theoretical and Applied Mechanics,2016,48(3):593-598(in Chinese))

2赵海峰,石俊,王斌斌.海上浮油定位浮标的力学分析与尺寸优化.力学学报,2016,48(1):235-242(Zhao Haifeng,Shi Jun,Wang Binbin.Mechanical analysis and sizing optimization of o ff shore oil slick tracking buoy.Chinese Journal of Theoretical and Applied Mechanics,2016,48(1):235-242(in Chinese))

3徐道临,卢超,张海成.海上浮动机场动力学建模及非线性动力响应特性.力学学报,2015,47(2):289-300(Xu Daolin,Lu Chao,Zhang Haicheng.Dynamic modeling and nonlinear characteristics of fl oating airport.Chinese Journal of Theoretical and Applied Mechanics,2015,47(2):289-300(in Chinese))

4 Isaacson M,Cheung KF.Second order wave di ff raction around twodimensional bodies by time-domain method.Applied Ocean Research,1991,13(4):175-186

5 Grilli ST,Guyenne P,Dias F.A fully non-linear model for threedimensional overturning waves over an arbitrary bottom.International Journal for Numerical Methods in Fluids,2001,35(7):829-867

6 Jamois E,Fuhrman DR,Bingham HB,et al.A numerical study of nonlinear wave run-up on a vertical plate.Coastal Engineering,2006,53(11):929-945

7 FuhrmanDR,MadsenPA.Simulationofnonlinearwaverun-upwith a high-order Boussinesq model.Coastal Engineering,2008,55(2):139-154

8 Pelinovsky E,Kharif C,Talipova T.Large-amplitude long wave interaction with a vertical wall.European Journal of Mechanics-B/Fluids,2008,27(4):409-418

9孙英伟.直立堤前的破碎波流场特征及波浪力研究.[博士论文].大连:大连理工大学,2012(Sun Yingwei.A study of breaking wave fl ow fi eld in front of the vertical breakwater and wave force.[PhD Thesis].Dalian:Dalian University of Technology,2012(in Chinese))

10 Chatjigeorgiou IK,Molin B.Third-order interactions,wave run-up and hydrodynamic loading on a vertical plate in an in fi nite wave fi eld.Applied Ocean Research,2013,41:57-64

11 SuCH,MirieRM.Onhead-oncollisionbetweentwosolitarywaves.Journal of Fluid Mechanics,1980,98:509-525

12 Fenton JD,Rienecker MM.A Fourier method for solving nonlinear water-wave problems:Application to solitary-wave interactions.Journal of Fluid Mechanics,1982,118:411-443

13 Kim SK,Liu PLF,Liggett JA.Boundary integral equation solutions for solitary wave generation,propagation and run-up.Coastal Engineering,1983,7(4):299-317

14 Power H,Chwang AT.On re fl ection of a planar solitary wave at a vertical wall.Wave Motion,1984,6(2):183-195

15 Cooker MJ,Weidman PD,Bale DS.Re fl ection of a high-amplitude solitary wave at a vertical wall.Journal of Fluid Mechanics,1997,342(1):141-158

16 Maiti S,Sen D.Computation of solitary waves during propagation and runup on a slope.Ocean Engineering,1999,26(11):1063-1083

17 Liu PLF,Al-Banaa K.Solitary wave runup and force on a vertical barrier.Journal of Fluid Mechanics,2004,505:225-233

18 Jian W,Sim SY,Huang Z,et al.Modelling of solitary wave runup on an onshore coastal cli ffby smoothed particle hydrodynamics method.Procedia Engineering,2015,116:88-96

19 Park H,Cox DT.Empirical wave run-up formula for wave,storm surge and berm width.Coastal Engineering,2015,115:67-78

20 Chambarel J,Kharif C,Touboul J.Head-on collision of two solitary waves and residual falling jet formation.Nonlinear Processes in Geophysics,2009,16:111-122

21宣瑞韬,吴卫,刘桦等.双孤立波直墙爬高的实验研究.水动力学研究与进展A辑,2013,03:241-251(Xuan Ruitao,Wu Wei,Liu Ye,et al.An experimental study on run-up of double solitary waves against a vertical wall.Chinese Journal of Hydrodynamics A,2013,03:241-251(in Chinese))

22 Carbone F,Dutykh D,Dudley JM,et al.Extreme wave runup on a vertical cli ff.Geophysical Research Letters,2013,40(12):3138-3143

23 Green AE,Laws N,Naghdi PM.On the theory of water waves//Proceedings of the Royal Society of London A:Mathematical,Physical and Engineering Sciences.The Royal Society,1974,338:43-55

24 Green AE,Naghdi PM.A derivation of equations for wave propagation in water of variable depth.Journal of Fluid Mechanics,1976,78:237-246

25 Zhao BB,Ertekin RC,Duan WY.A comparative study of di ff raction of shallow-water waves by high-level IGN and GN Equations.Journal of Computational Physics,2015,283:129-147

26 Zhao BB,Duan WY,Ertekin RC.Application of higher-level GN theory to some wave transformation problems.Coastal Engineering,2014,83:177-189

27 Ning D,Teng B,Zhao H,et al.A comparison of two methods for calculating solid angle coefficients in a BIEM numerical wave tank.Engineering Analysis with Boundary Elements,2010,34(1):92-96

28 Ning D.Zhuo X,Teng B.Focused waves interaction with a vertical wall//Twenty-third(2013)International O ff shore and Polar Engineering,Alaska,USA,June 30–July 5,2013

NONLINEAR NUMERICAL STUDY OF NON-PERIODIC WAVES ACTING ON A VERTICAL CLIFF1)

Li Xiang Zhang Chongwei Ning Dezhi2)Su Peng
(State Key Laboratory of Coastal and O ff shore Engineering，Dalian University of Technology，Dalian 116024，China)

In this study,a 2D fully-nonlinear numerical wave tank is developed based on the time-domain higher-order boundary element method.Non-periodic waves acting on a vertical cli ffare investigated.The fully nonlinear kinematic and dynamic boundary conditions are satis fi ed on the instantaneous free surface.The mixed Eulerian-Lagrangian method is adopted to track the transient water particle on the free surface and the fourth order Runge-Kutta method is used to predict the velocity potential and wave elevation on the free surface.Then the acceleration potential technique is adopted to calculate the temporal derivative of the potential on the vertical wall surface,and transient wave loads are obtained by integrating the Bernoulli equation along the wetted wall surface.The obtained nonlinear results are fi rstly compared with solutions of the Serre-Green-Naghdi(SGN)theory.It is observed that,for the highly nonlinear case of double-incidentwaves,the SGN model which only satis fi es the weak dispersion relationship greatly underestimates the maximum wave run-up(MWR).Then,the nonlinear interaction between double-incident-waves and a vertical cli ffis further studied.It is found that the linear prediction also underestimates the MWR.The nonlinearity not only leads to an evident increase of the MWR,but also results in a high-frequency oscillation of the free surface.During this process,nonlinear properties of wave loads are similar to those of the wave run-up.Finally,spectral analysis is performed on histories of wave run-up and wave loads.The dominant frequency wave component is found to transfer its energy to higher frequency components,as a typical nonlinear wave-wave interaction phenomenon.

nonlinear wave,wave run-up,time-domain simulation,higher-order BEM,GN theory

O353.2

A

10.6052/0459-1879-16-337

2016–11–20收稿，2017–07–21 录用,2017–07–21 网络版发表.

1)国家自然科学基金(51679036，51490672)，水文水资源与水利工程科学国家重点实验室开放基金(2016490111)和中央高校基本科研业务费专项资金(DUT17GJ202,DUT16RC(3)113)资助项目.

2)宁德志，教授，主要研究方向：海岸和海洋工程中水动力学.E-mail：dzning@dlut.edu.cn

李翔，张崇伟，宁德志，苏朋.非周期波浪与直墙作用的非线性数值研究.力学学报,2017,49(5):1042-1049

Li Xiang,Zhang Chongwei,Ning Dezhi,Su Peng.Nonlinear numerical study of non-periodic waves acting on a vertical cli ff.Chinese Journal of Theoretical and Applied Mechanics,2017,49(5):1042-1049