汽车零部件平准化拣配作业优化研究

陈正丰，董宝力

(浙江理工大学 机械与自动控制学院，浙江 杭州 310018)

汽车零部件平准化拣配作业优化研究

陈正丰，董宝力

(浙江理工大学 机械与自动控制学院，浙江 杭州 310018)

针对汽车零部件拣配作业工作效率低、工作负荷不均衡及配送车辆装载率低的问题，以作业人员工作负荷均衡化和配送车辆装载率最大化为目标，建立汽车零部件平准化拣配作业优化模型.模型求解过程分为两级：运用启发式算法确定动态作业人员分配方案；在作业人员合理分配基础上利用遗传算法确定换装顺序及车辆装载计划.实例分析结果显示，与原拣配作业方案相比，该模型使车辆装载率提高了 18.4%，作业总工时减少了 26 h.

汽车零部件；平准化；物料拣配；作业者分配；装载率

仓储是物流的重要一环，它主要有接收物料、储存物料、根据顾客订单拣选配送货物三大功能.在汽车零部件物流仓储拣选配送作业中，零部件转换包装(以下简称换装)的出货作业比较耗时，会产生较大的运营成本.合理优化作业人员配置、作业顺序和装车配送计划，对仓储拣配作业效率的提升具有重要意义.

针对物料拣配，目前国内外学者的主要研究，集中于拣料路径和存储方式的优化及配送过程中车辆装载率和路径问题(Vehicle Route Problem, VRP).陈庆喜等通过改进拣料路径和分类存储方式提高了人工拣配效率[1].曾敏刚等提出零部件循环取货入厂物流平准化的运作模式，并给出平准化(heijunka)循环取货的操作流程，详细对比了订单平准化、集货平准化和接收平准化与非平准化的效果[2].徐克林等对配装-运输集成问题进行研究，建立了配装-运输集成决策(Loading-Transportation Integrated Decision-making，LTID)模型[3].党立伟等为研究有限配送车辆情况下物料准时化配送问题，采用改进遗传算法和三阶段启发式算法进行了求解[4].高贵兵等提出了以降低配送车辆成本为优化目标的混合多目标车辆路径优化模型[5].赵晏林等采用改进遗传算法求解了从运输成本、换装成本和时间惩罚成本角度建立的多式联运网络优化模型[6].这些研究针对配送路径和车辆装载的最优化问题提出了模型，但是对于物料配送前期备料过程的作业模式研究较少.本文从汽车零部件换装作业人员工作量均衡及配送车辆效率提升综合最优的角度出发，对换装区的作业人员数量分配、换装顺序和装车计划进行系统性分析，提出一种平准化零部件拣配作业模型.

1 问题描述及中储零部件平准化配送作业策略

1.1问题描述

对于外地生产的零部件，国内大部分汽车制造厂都是通过指定物流商对零部件进行短途循环取货后，进入区域集货中心，换作干线运输并由卡车运输到汽车主机厂附近的中转仓库(以下简称中储)，再从中储要货出库短途运输到主机厂[7].中储收到主机厂要货订单后安排拆分、换装和出库.中储一般有多个换装区，现行的作业流程如下：①每个换装小组负责完成本组的换装任务；②每天早上各小组领取自己的任务单；③换装人员逐个完成供应商当日所有的换装任务，并将货物送至发货暂存区；④出货人员根据出货平台的零部件扫描出货.但是，现行的换装出货作业方式存在一些突出问题.

(1)各换装组人数基本固定不变，但换装区每日实际作业量却是变动的，导致各换装区人员日工作负荷不均衡.

(2)当日计划未切割，经常出现先换装完成的零部件积压在发货暂存区或主机厂收货口；未完成换装的零部件不能及时发往主机厂，往往需要主机厂发出紧急拉动订单.

(3)无详细的换装作业与装车配送计划，配送车辆装载率低，配送车辆在出货平台等待时间较长.

1.2中储零部件平准化拣配作业策略

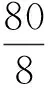
图1 平准化拣配作业流程

2 汽车零部件平准化拣配作业模型

汽车零部件平准化拣配作业模型有两个优化目标：目标1是确定最合理的人工分配方案，使换装作业人员工作负荷均衡化；目标2是确定作业顺序和装车计划，使配送车辆装载率最高，且同时确保完工时间点差异小的任务装载于同一辆配送车上，首先完成换装作业的任务优先装车配送.

2.1目标函数F1

目标函数F1是作业总工时最小,即：

(1)

式中：换装区i=1，2，…，m；Tri为换装区i分配换装人员后换装实际总用时.

(1)引入一个 0-1 决策变量Yij，定义为：

(2)

(2)各换装区换装出货总用时为：

(3)

式中：j为供应商，j=1，2，…，n；Tij为i区中j供应商一个标准单位托盘换装的处理时间，如换装时间、码垛时间及贴标签时间；Vij为i区中j供应商订单零部件的体积；Tpi为i区中一个单位托盘换装的出货时间.出货时间与出货距离及换装人员行走速度有关，同一换装区的出货时间默认相同，出货托盘最大体积不能超过1 m3，不同供应商的零部件不能混放.

(3)各换装区的出货时间为：

(4)

式中：2Li为换装区i的出货往返距离；v为换装人员的行走速度.

(4)各换装区的理论分配人数为：

(5)

式中：R为换装人员总数.Ri不一定是整数，按照相应规则处理，得到每个换装区实际分配的拣货人数Rai.

(5)实际分配人数后各换装区完工总用时为：

(6)

(6)各区分配的人数之和等于实际工人数，即：

(7)

2.2目标函数F2

目标函数F2是一个多目标的总目标函数，用于确定最合理的装车配送计划与换装作业顺序.

(8)

式中：k为配送车辆车次，k=1，2，…，z(z是一个待决策变量)；Pk是第k辆配送车的实际装载率；Sk是配送任务完工时间标准差；Tk是配送任务最大完工时间点；μ为比例系数.

(1)引入两个 0-1 决策变量，定义为：

(9)

(10)

(2)第k辆配送车的实际装载率为：

(11)

式中：U为第k辆配送车的容积.

(3)配送车辆k在不同换装区配送任务的完工时间标准差为：

Sk=

(12)

式中：TSik为第k辆车所配送的i区换装任务作业开始时间，当k=1时，TSik=0；Trij为供应商j的实际完工用时.

(13)

(14)

(4)配送车辆k的任务最后完工时间为：

(15)

(5)所有供货任务都将被配送，且同一任务只能装载于同一辆配送车上，即：

(16)

(17)

式中：V为该分割批次订单的零部件总体积.

(6)车辆不能超载，即：

(18)

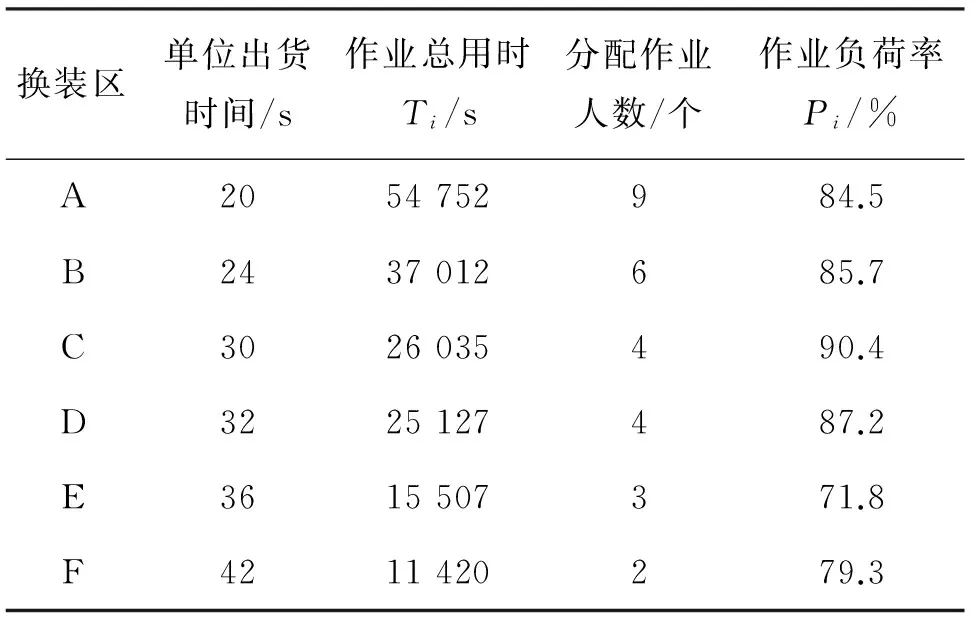
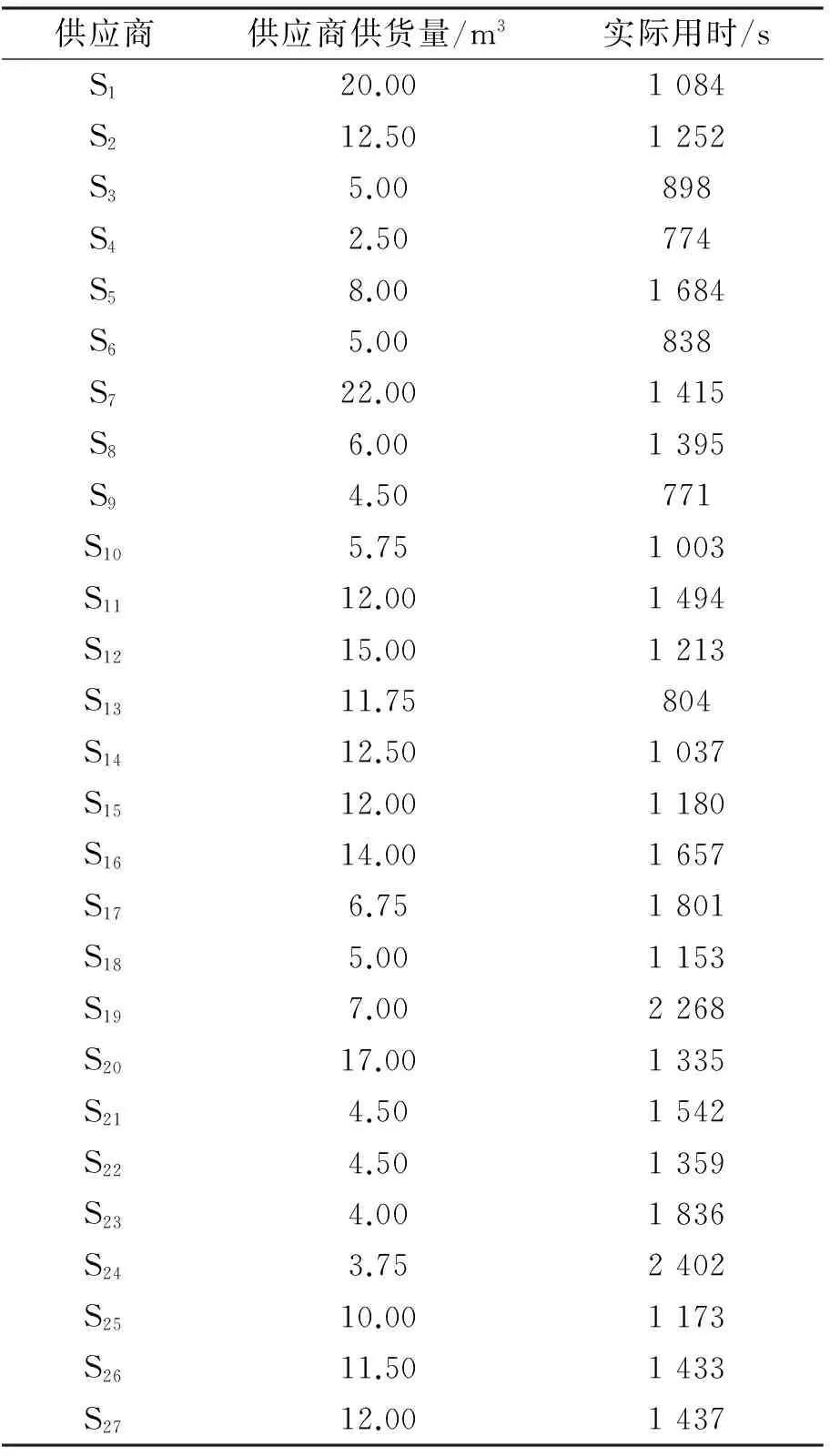
式中：Vk为配送车辆k能装载的最大体积，Vk

3 算法设计

中储零部件平准化配送作业的优化求解过程分为两级：第一级，确定各换装区最合理的换装人员数；第二级，在给定人员数合理分配的前提下决定最合理的换装顺序以及车辆装载计划.

3.1换装人员调度配置优化算法

中储分区同步换装系统动态分配作业人员属于生产调度问题.启发式算法具有计算效率高和算法灵活等优点[9].本文算法设计如下：首先，求解某个分割批次换装区i需要的总拣货时间Ti，分别对每次换装时间、出货时间进行求解；然后，求解每个换装区分配的理论作业人数Ri，使得整个拣配过程耗时最少.

步骤1：获取某批次换装区i的任务，计算出任务中各供应商零部件的体积数Vij.

步骤2：求解换装区到发货暂存区的用时Tpi.Tpi由式(4)求得.

步骤4：将步骤1、步骤2、步骤3求解的值代入式(3)，求解出该批次i区完成作业所需总时间Ti.

步骤5：按照式(5)求解Ri.

3.2换装顺序及装车配送计划优化算法

3.2.1 编码设计

表1所示为某配送中心各换装区的作业任务.染色体基因采用自然数编码，将所有拣配任务排成一列进行编码，s个任务代表s个基因，基因位上的信息为配送车辆编号(图2)[10-11].这种编码方式的优点是便于计算各配送车辆的装载率.

表1 某配送中心各换装区作业任务

图2 基因的编码与解码

3.2.2 种群初始化

用车辆编号对拣配任务进行标记，被标记的基因位表示分配到了相应车辆.当某一配送车辆标记的配送任务的体积超过Vk时，将最后一个标记的任务分配至下一配送车辆，直至所有基因位被标记完成.重复以上操作，直到获得N条染色体数量的初始种群.每条染色体都是一个受作业时间、配送时间、车辆装载空间约束的可行解编码.

3.2.3 适应度函数

目标函数F2是求最小值，所以本文将适应度函数设置为目标函数F2的倒数.目标函数值越小，其适应度就越优，即：

(19)

3.2.4 选择操作

采用适应度值概率分布的轮盘赌法选择染色体[11]，保留所有染色体中适配值最优的染色体，采用轮盘赌法在其余染色体中选出累积概率高的个体进入下一代.

3.2.5 交叉与变异操作

交叉操作产生新个体.本文按交叉概率随机在当前群体中选择两条染色体，交换某些片段获得新的个体染色体.对选定的两条染色体以一个小于车辆数的随机整数r作为交叉点，染色体1中基因值小于r的元素被复制到新的染色体中.新的染色体中剩下的基因位由染色体2中基因值大于r的元素填充.

变异操作能够加速求解过程.设染色体参加变异的概率为Pm，种群中部分染色体按照变异概率进行变异，产生相应数量的新染色体来替换之前选出的染色体.

4 案例分析

某中储仓库距离主机厂5 km，实行日夜两班制8 h工作制，每班共有28人负责换装作业.配送车辆的规格为：9.6 m×2.4 m×2.4 m=55 m3，允许装载货物的最大体积为46 m3，即允许的最大装载率为83.6%.单日订单主要涉及27个供应商，货物总量为2 036 m3，共发送63车次，平均装载率为58.7%.换装区与供应商的对应关系如表2所示.当日各班次进行1 h的加班，则人员作业总工时为：(8+1)×13×2+15×8×2=474(h).

表2 换装区与供应商的对应关系

采用零部件平准化拣配方式对当日作业进行模拟，对供应商日供货量进行8次分割，每个批次作业时间T=7 200 s.供应商日出货量平准化数据如表3所示.

表3 供应商日出货量平准化数据

4.1确定各组换装人员数

运用换装人员调度配置优化算法可求解各换装区最优人员数.人员分配方案及各换装区作业负荷率如表4所示.

表4 换装区人员分配优化方案

由表4可知：各班次均能在正常上班时间内完成作业任务；优化后的人员作业总工时为：28×8×2=448(h)，比原作业方式的作业总工时节省了26 h.

4.2确定换装顺序及装车配送计划

表5所示为每个批次供应商的供货量及人员分配方案确定后供应商的实际拣配作业用时.

人员分配方案确定后，在换装作业顺序与装车计划优化算法中采用MATLAB2015进行仿真.其仿真参数为：种群数量N=100，最大遗传代数MAXGEN=400，交叉概率PC=0.70，变异概率Pm=0.05，μ=ρ=0.01.仿真得到的目标函数变化曲线即为种群最优值(图3).

表5 供应商换装作业实际用时

图3 遗传算法的目标值与种群均值变化曲线

从图3可以看出，种群在迭代次数为55时收敛至最优.最优解对应染色体解码的零部件换装顺序及装车计划方案如表6所示.由表6可知：单批次所有任务共需6车次完成配送；当日所有任务共需要48车次完成，比原作业方式节省15车次；配送车辆平均装载率为77.1%，比原作业方式提升了18.4%.

表6 零部件供应商换装顺序及装车计划优化方案

5 结束语

本文介绍了基于工作量均衡的物料换装作业人员分配及提升配送车辆装载率的汽车零部件拣配作业方案.对某物流中储验证表明，新的作业模式能有效提升中储拣配作业效率，提高配送车辆装载率，减少紧急拉动订单数.零部件平准化拣配作业可以实现入厂物流过程中稳定的零部件配送频率和货物量，对整个供应链的运营成本控制具有较大的实际意义.

[1] 陈庆喜,周奇才,范思遐. 某人工拣配库的优化分析和模型建立[J]. 珠江水运,2012(14):35-37.

[2] 曾敏刚,苏水清,李永麒. 基于循环取货的零部件入厂物流平准化研究[J].工业工程与管理,2011,16(2):40-45.

[3] 徐克林,朱 伟,李艳冰. 配装-运输集成决策模型及其遗传算法[J]. 浙江大学学报(工学版),2011,45(9):1630-1635.

[4] 党立伟,孙小明.基于配送BOM的装配线物料循环准时化配送研究[J].机械制造,2012,50(7):89-91.

[5] 高贵兵,张红波,张道兵,等.混流制造车间物料配送路径优化[J].计算机工程与应用,2014,50(15):228-234，270.

[6] 赵晏林，李 琴，黄 丽.基于改进遗传算法的多式联运网络优化[J].成组技术与生产现代化，2015，32(2):23-31.

[7] 马 钧,缪震环,申丽莹. 大众与丰田零部件入厂物流模式对比研究[J]. 汽车工业研究,2014(5):49-52.

[8] 王超然. 基于循环取货的机动车零部件入厂物流整合[D].天津：天津大学,2012.

[9] 雷 斌,蒋兆远,马殷元.配送中心分区同步拣货系统人员分配策略研究 [J]. 计算机工程与应用,2014,50(24):4-9,41.

[10] 张新敏,李 亮,刘 设.基于改进遗传算法的汽车混流装配线物料配送路径优化[J]. 物流科技,2016,39(2):16-20.

[11] 李 伟,董宝力.基于空箱拉动的总装线物料配送研究[J].成组技术与生产现代化，2016,33(1):21-26，40.

ResearchonHeijunkaforPartsDistributionWorkofAutomobile

CHEN Zheng-feng, DONG Bao-li

(School of Mechanical Engineering and Automation,Zhejiang Sci-Tech University,Hangzhou 310018,China)

Aimed at low working efficiency，work load imbalance and vehicle cubed out low of the automobile parts picking and distributing，to the operator work load equalization and the delivery vehicle cubed out maximization as the goal，set up picking and distributing operation optimization model of the leveling of automobile parts. The process of model solving is divided into two levels: using heuristic algorithm to determine the dynamic operator allocation scheme；The genetic algorithm is used to determine operation sequence and vehicle distribution plan. The results show that compared with the original sorting scheme，the model makes the loading rate of the vehicle increased by 18.4%，and the total work time is reduced by 26 hours.

automobile parts；heijunka；material distribution；laborer allocation；vehicle cubed out

2017-05-04

陈正丰(1992-)，男，湖南邵阳人，硕士研究生，研究方向为精益生产及供应链管理.

1006-3269(2017)03-0047-07

TP30

A

10.3969/j.issn.1006-3269.2017.03.011