小型无人机弹射系统的动力学研究

胡 明，刘 高，梁振刚

(1.沈阳理工大学 装备工程学院，辽宁 沈阳 110159；2.重庆建设工业(集团)有限责任公司，重庆 400054)

小型无人机弹射系统的动力学研究

胡 明1，刘 高2，梁振刚1

(1.沈阳理工大学 装备工程学院，辽宁 沈阳 110159；2.重庆建设工业(集团)有限责任公司，重庆 400054)

为发挥小型无人机的作战效能，设计了一款弹簧式小型无人机发射系统，建立了无人机发射系统的物理模型和动力学模型，并对弹射过程进行动力学仿真，得到了无人机发射系统的运动曲线.研究表明，这种小型无人机发射系统采用弹簧作为动力源，结构简单，原理可行，能够使无人机获得所需的起飞速度.

小型无人机；弹簧；发射；动力学

无人机发射系统是保证无人机机动灵活、重复使用以及高生存能力的一个重要功能系统.无人机的发射方式多种多样，包括母机投放、火箭助推、车载滑跑起飞、垂直起飞、弹射起飞、手抛发射等方式，其中弹射起飞方式应用最为广泛[1].弹射起飞方式对结构要求比较简单，又易于控制，且在发射过程中不会产生光、热、烟等[2]，便于发射系统和人员的隐蔽.但是，目前为止，对无人机发射系统的研究主要集中在中大型无人机上，对小型及微型无人机的投放器研究匮乏，特别是在针对特定无人机设计匹配的发射机构方面缺乏清晰的理论认识[3].孙志宏对无人机橡筋动力弹射、电机动力弹射、气液压筒动力弹射等几种方式的原理、优点及应用等进行了说明[4]；禹勇等对无刷直流电机驱动定距螺旋桨作为动力装置的无人机进行了建模和仿真研究[5]；杨康等对无人机的发射控制方式进行分析，并实现了联合发射控制方式[6]；权凌霄等对无人机气液压弹射系统建模与弹射过程进行仿真分析，得出了影响无人机起飞速度的关键因素[7].对于微、小型无人机来说，在有限的发射空间内储存足够的能量并使之转化为动能，又不增加冗余重量是发射系统设计与分析的重点.

本文在综合无人机现有发射技术的基础上，设计了一款弹簧式小型无人机发射系统.该系统以弹簧作为动力源，在发射过程中对无人机做功，提供无人机起飞能量.无人机发射完成后，其发射构件自动复位而进入下一发射循环.整套发射系统由弹簧和齿轮、齿条组合构成，结构较简单，可靠性较高，系统质量较小[8]，在应对复杂战场环境方面具有一定的优势.本文针对该小型无人机发射系统进行动力学研究，对发射过程关键影响因素进行分析，以期为小型无人机发射系统的研究做出铺垫.

1 无人机弹射系统的组成和工作原理

1.1系统基本组成

无人机弹射系统的结构组成如图1所示.它主要由发射架座、动力簧、缓冲簧、启动电源、助力齿轮、电机、齿条、缓冲垫等组成.

图1 无人机弹射系统结构示意图

1.2系统工作原理

弹射式发射系统以动力簧作为发射动力，不完全助力齿轮—齿条作为传动装置.发射之前，利用外能源带动不完全助力齿轮转动，通过助力齿轮与齿条啮合作用，带动齿条向后运动.同时，齿条上的压板向后运动并压缩动力簧，将无人机加载到发射架座上.当助力齿轮转动到齿弧的边缘时，动力簧的压缩量达到最大，其弹性势能也达到最大，发射动力的储存工作完成.当助力齿轮转过齿弧边缘时，齿条与不完全助力齿轮脱离啮合，齿条失去齿轮力的作用且无法继续压缩动力簧而使之解脱.动力簧在解脱后迅速恢复至自由高度，在恢复自由高度的过程中，动力簧弹性势能得到释放并将齿条与无人机一起弹射出去.齿条在向前运动的过程中撞击由缓冲垫和缓冲簧组成的缓冲组件而逐渐降速，避免了齿条与机匣发生剧烈碰撞.齿条在定位爪的作用下停止运动，无人机在动力簧释放的弹性势能作用下加速运动，离开发射架座而起飞升空，随后自身动力源开始工作.

2 无人机弹射系统动力学模型的受力分析

在无人机发射过程中，无人机弹射系统的运动可简化成一个两自由度的弹簧-质量系统.其物理模型如图2所示.在此模型中，采用多刚体静力学分析理论，以无人机能够获得的最小起飞能量和最低起飞速度为约束条件，认为无人机达到最低起飞速度即可完成升空而不考虑风阻、射角、落高等因素.分析时将无人机的质量加载到齿条上，以便以质点等效代替各构件的质量.

图2 无人机弹射系统的物理模型

设齿条、无人机和缓冲垫的质量分别为mc、mw、mh，齿条和缓冲垫的位移分别为xc和xh，齿条长度为lc，轨道长度为x，发射架座与齿条、缓冲垫的摩擦力分别为Ffc、Ffh，齿条与助力齿轮之间的摩擦力为Ffz，齿条与无人机之间的摩擦力为Ffw，作用于齿条的力有动力簧力Fd、助力齿轮力Fz，作用于缓冲垫的力主要是缓冲簧力Fh.以发射开始状态的动力簧后端面(图2所示左端)为坐标原点O,建立坐标系xOy，以无人机发射方向为正，即x轴正向.该系统一个循环过程可分为3个阶段.

2.1助力齿轮开始带动齿条后移到齿条压缩动力簧至最大弹性势能位置(第一阶段)模型的受力分析

该阶段齿条受到助力齿轮力和动力簧的反作用力作用，发射架座与齿条之间、齿轮与齿条之间发生摩擦作用.该阶段进行模型受力分析的边界条件为：-xdmax≤xc<0.其中，xdmax为动力簧最大压缩量.其受力过程如图3所示.

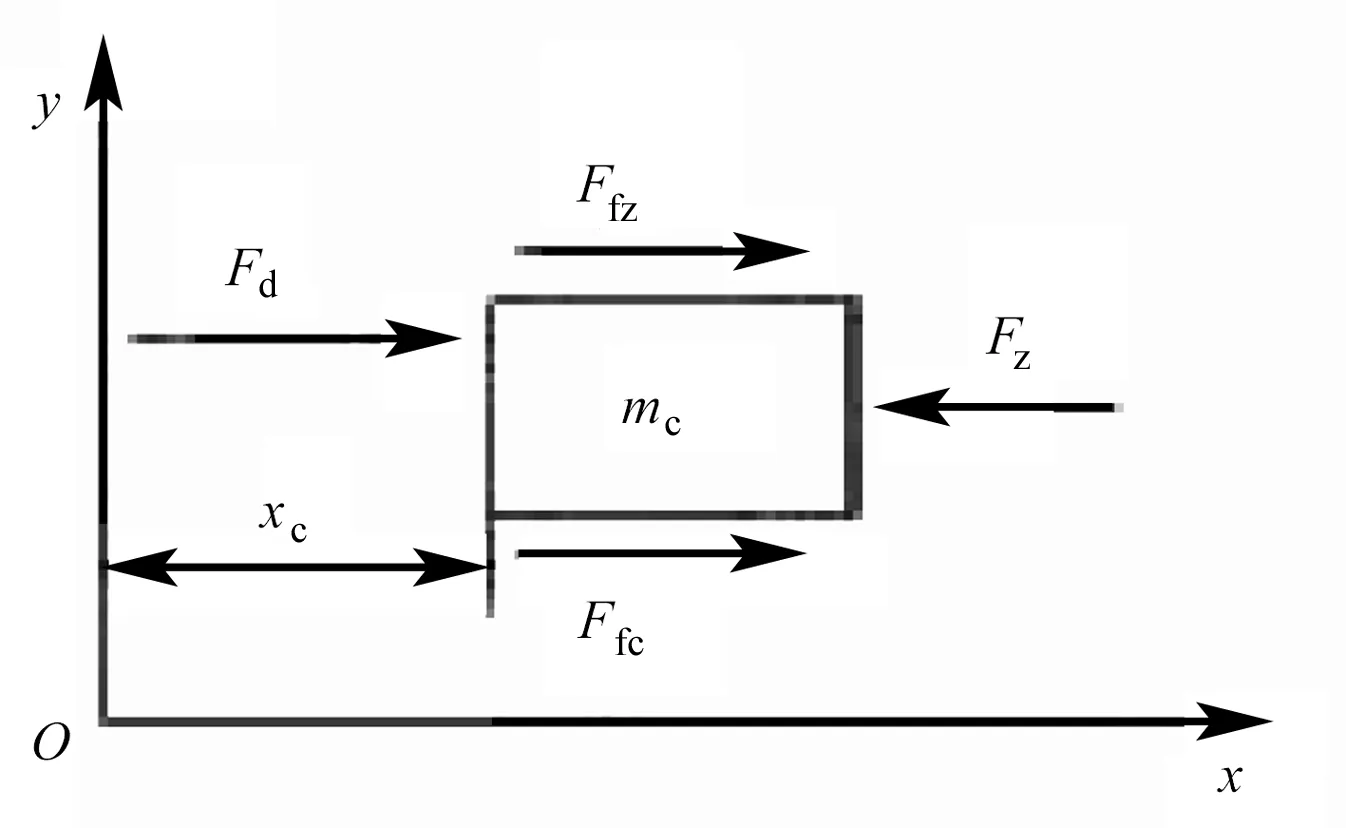
图3 无人机弹射系统第一阶段的动力学模型

根据图3所示，助力齿轮力Fz克服阻力对齿条做功，压缩动力簧蓄积弹射能量，可推导出该阶段齿条的运动方程组：

(1)

式中：Fd=F0d+kdxc，F0d为动力簧预压力，kd为动力簧的刚度系数；Ffz=fzmc，fz为齿条与助力齿轮之间的动摩擦因数；vc为齿条运动速度；P为电动机额定功率.

2.2动力簧弹性势能释放而推动齿条及无人机弹射起飞(第二阶段)模型的受力分析

该阶段将无人机安放在齿条上，解脱齿条，无人机起初在齿条摩擦力作用下，与动力簧作用下的齿条相对于地面同步沿发射架座轨道向前滑动，无人机在发射轨道上有相对运动.在动力簧弹性势能释放完毕，齿条接触缓冲垫的临界状态，无人机获得最大起飞速度，滑出轨道起飞,完成发射动作.该阶段进行模型受力分析的边界条件为：00.其受力过程如图4所示.

图4 无人机弹射系统第二阶段的动力学模型

图4所示，无人机在动力簧蓄积的能量作用下获得弹射速度.根据牛顿第二定律和速度位移关系可得出该阶段齿条与无人机的运动方程组：

(2)

式中：Ffw=fwmw，fw为无人机与齿条之间的动摩擦因数；vw为无人机起飞速度；t2为第二阶段时间常数.

2.3齿条压缩缓冲垫至缓冲完毕而齿条复位(第三阶段)模型的受力分析

该阶段动力簧弹性势能释放完毕，无人机发射升空.考虑到齿条须在动力簧作用下复位，如果它直接接触架座内壁就会形成刚性碰撞，对发射系统构件造成损伤，因而加装缓冲装置，使缓冲簧在弹性势能将要释放完毕时发挥作用，保证齿条安全复位.该阶段进行模型受力分析的边界条件为：xc=xdmax,xh>0.其受力过程如图5所示.

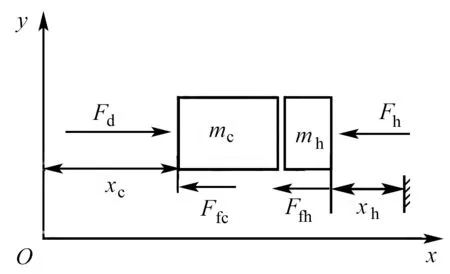
图5 无人机弹射系统第三阶段的动力学模型

图5所示，助力齿条使小型无人机获得弹射初速度之后，依托缓冲垫作用抵消剩余能量，并恢复到初始位置.根据牛顿第二定律和速度位移关系、能量守恒定律，可得到该阶段齿条与缓冲垫的运动方程组：

(3)

式中：Fh=khxh，kh为缓冲簧的刚度系数；Ffh=fhmh，fh为缓冲垫与发射架座之间的动摩擦因数；vh为缓冲垫的运动速度；t3为第三阶段时间常数.

3 无人机弹射系统的动力学仿真计算

采用MATLAB软件[9]对无人机发射过程的3个阶段按照边界条件以分段函数的形式编制仿真程序.在仿真程序中，第一、第二阶段以动力簧变化量xc作为自变量，第三阶段以缓冲垫缓冲簧的变化量xh作为自变量，对无人机发射系统进行仿真计算，求解无人机与助力齿条的速度位移曲线，然后分别改变齿条的长度和动力簧的刚度系数，分析对比不同参数下的速度位移曲线，获取影响无人机弹射的相关因素.仿真的主要结构参数[10]如表1所示.

助力齿轮带动齿条是通过啮合关系实现的，因而可以忽略Ffz，同时忽略内部微小碰撞.通过仿真计算，得到了无人机起飞速度和齿条速度关于位移的变化曲线(图6).

表1 小型无人机弹射系统仿真的主要结构参数

图6 齿条及无人机速度-位移曲线

在[-0.15,0]位移区间内，齿轮在电动机固定转速带动下转动，齿条在助力齿轮的作用下沿x反方向匀速前进，此时加速度为0；在[0，0.15]位移区间内，助力齿轮解脱齿条，齿条在动力簧弹性势能作用下沿x正向加速运动，当x=0.15 m时，齿条速度达到最大值，之后齿条在缓冲簧作用下减速，直到速度为0.无人机在[0,0.30]位移区间内速度逐渐达到起飞要求.在[0,0.15]位移区间内，由于无人机依靠齿条的弹性势能获得初速，因而无人机速度变化趋势与齿条速度变化趋势相近，但存在相对滑动.在x=0.15 m时，vc=vw，此时无人机脱离齿条，继续在发射轨道内滑动，直到轨道终点.此时按照要求的起飞速度vw≥10 m/s，无人机进入发射空域飞行.

从建立的动力学模型和图6可知，影响发射状态的参数有动力簧刚度系数kd、齿条长度lc、轨道长度x等.由于小型无人机弹射系统需要考虑人机工效、无人机质量等因素，轨道长度x需要控制在一定范围，改变x对于无人机发射速度的提升作用有限，故而，可选取3组不同的动力簧刚度系数kd和齿条长度lc进行仿真计算，得出无人机起飞速度-位移曲线.

齿条长度lc=0.30 m，动力簧刚度系数分别取kd1=100 N/m、kd2=150 N/m、kd3=200 N/m时，无人机起飞速度随位移的变化曲线如图7所示.从图7可以看出：无人机的起飞速度与位移呈线性关系，这与动力簧的弹簧力变化是相关的；在给定位移变化区间内，刚度系数越大，速度上升得越快，达到的起飞速度越大.但是，刚度系数的选择需要根据实际的无人机结构确定，若刚度系数过大，则结构动作实现时存在困难.从图6也可看出，无人机在位移为0时，速度不为0.这是由于相对于地面，无人机的位移变化区间为[0,0.30]，但是无人机相对于齿条是存在滑动的，因而无人机初始速度不为0.

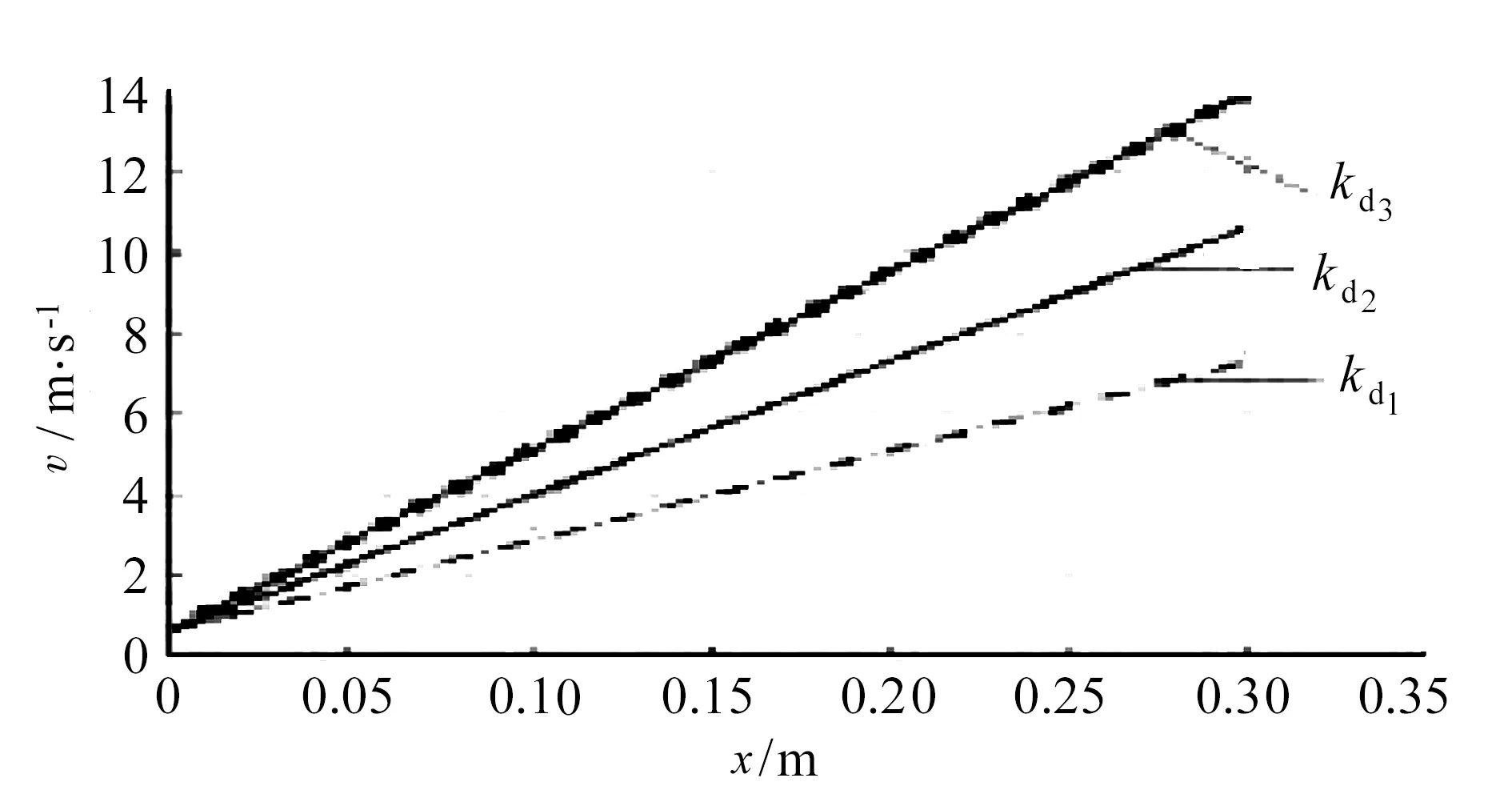
图7 动力簧不同刚度系数时无人机起飞速度-位移曲线

无人机弹射系统弹簧刚度系数kd=150 N/m，齿条长度分别为lc1=0.1 m、lc2=0.3 m、lc3=0.5 m时，无人机起飞速度随位移的变化曲线如图8所示.从图8可以看出，在一定刚度系数和一定位移的情况下，无人机起飞速度随着齿条长度的增加而增大.但是，齿条长度的改变对无人机起飞速度的影响相对于弹簧刚度系数的影响要小，并且无人机的初始速度随着齿条长度的增加而增大.

图8 不同齿条长度时无人机起飞速度-位移曲线

4 结束语

(1)弹簧式小型无人机发射系统发射无人机时，无人机起飞速度的变化趋势与齿条长度呈线性关系，并与动力簧的变化趋势相关.在给定齿条长度lc=0.3 m时，动力簧刚度kd≥150 N/m时才能满足无人机的起飞条件.

(2)在考虑人机工效的前提下，忽略轨道长度的影响，则动力簧的刚度系数、齿条长度等因素共同决定无人机的起飞速度.

(3)需要减小弹簧刚度系数时，可相应增加轨道长度，以保证无人机要求的起飞速度.

(4)在给定刚度系数条件下，设计的弹簧式无人机发射系统结构简单，原理可行，能够使无人机获得所需的起飞速度.

[1] 苏 倩.无人机动力系统及弹射装置的研究[D].哈尔滨：哈尔滨工业大学，2008:1-4.

[2] 张 博.无人机磁耦合发射系统研究[D].长春：长春理工大学，2012:1-5.

[3] 李建华.某无人机发射系统技术研究[D].南京：南京理工大学，2008:1-3.

[4] 孙志宏.无人机弹射起飞技术分析[J].测绘与空间地理信息，2014，37(8):174-175.

[5] 禹 勇，董 凯，滕国飞，等.微小型无人机动力装置建模与仿真研究[J].信息通信，2016(5):4-5.

[6] 杨 康，罗卫兵.微小型无人机发射关键技术研究[J].现代电子技术，2013，36(21):120-123.

[7] 权凌霄，刘建伟，宋 豫，等.无人机气液压弹射系统建模与弹射过程仿真分析[J]. 液压与气动，2016(1):71-77.

[8] 苏子舟，张明安，国 伟，等．电磁无人机弹射应用综述[J]．火炮发射与控制学报，2011(1):93-96.

[9] 张德丰.MATLAB数值分析[M].北京：机械工业出版社，2012:150-170.

[10] 刘 斌，马晓平，王和平,等. 小型电动无人机总体参数设计方法研究[J].西北工业大学学报,2005，23(3):396-400.

DynamicsResearchontheSpringLoadedLaunchSystemofSmallUAV

HU Ming1,LIU Gao2, LIANG Zhen-gang1

(1.School of Equipment Engineering, Shenyang Ligong University, Shenyang 110159,China;2.Chongqing Construction Industry(Group) Limited Company,Chongqing 400054,China)

Lacking of knowledge of the launch process of the micro-UAV restricts the combat effectiveness of the UAV on the battlefield. This paper designed a spring-type launch system for small UAV, established the physical model and dynamic model of the UAV launch system, obtained the motion curve of the UAV launch system through the dynamic simulation for the ejection process and analyzed the results. The results showed that this kind of small UAV launch system uses spring as power resource. Its structure is simple, the principle is feasible, and the launching process of the UAV can be completed.

small unmanned aerial vehicle; spring; launch; dynamic

2017-07-13

辽宁省教育厅高校科研基金资助项目(L2014076)

胡 明(1983-)，男，辽宁沈阳人，博士研究生，讲师，研究方向为轻武器设计及仿真.

1006-3269(2017)03-0006-04

TM303.1

A

10.3969/j.issn.1006-3269.2017.03.002