基于BP神经网络的低压配电台区电压估算

尹忠东， 牟 锴， 金涌涛， 童 力， 赵启承

(1.华北电力大学 电气与电子工程学院，北京 102206；2.国网浙江省电力公司电力科学研究院，浙江 杭州 310014)

基于BP神经网络的低压配电台区电压估算

尹忠东1， 牟 锴1， 金涌涛2， 童 力2， 赵启承2

(1.华北电力大学 电气与电子工程学院，北京 102206；2.国网浙江省电力公司电力科学研究院，浙江 杭州 310014)

针对低压配电台区运行参数采集受限，无法实现电压全覆盖监测或电压精确计算的问题，在能够召测少数节点电压的情况下，提出基于少数据的BP神经网络电压估算算法。在总结低压配网可用参数的基础上，通过电压降落的近似计算，分析了低压配电网节点电压的影响因素，提出节点负荷矩的新概念，建立低压配网节点负荷矩——电压估算模型，并结合神经网络基于数据建模对输入输出特性的自学习能力，以少数节点数据为样本对配网全部节点电压进行估算。为防止神经网络在训练过程中陷入平坦区，在算法中添加加权因子，动态调整神经网络的学习率和动量因子，提高学习效率。采集实际配电网算例数据对算法进行验证，其误差满足估算精度要求，证明本文提出的方法具有可行性及适用性。

低压配电网； 节点负荷矩； BP神经网络； 电压估算； 误差动态调整

0 引 言

近年来，经济水平的提高使得居民的用电负荷快速增长，作为直接面向用户的电力系统终端，低压配电网的部分台区在用电高峰期经常出现电压偏低现象。电压质量的优劣直接关系到电力系统的安全、经济运行和电气设备的使用寿命，根据《供电营业规则》中要求[1]，220 V单相供电电压允许偏差为额定值的+7%、-10%。为防止或减少低压用户的出现，需要实时掌握配电网供电用户的电压状况，然而目前的监测和采集技术远远不能达到对每个用户电压的全覆盖监测。由于得不到实时监测或低电压治理，尤其在低压农网区域，容易出现首端电压监测合格，而末端电压偏低的现象。据对浙江省的调查，虽然全省24万台公用配变电压在实时监测下均处于合格范围，但只2015年1～2月份的统计就有2 900多户农村公变下的用户出现低电压。要减少和治理低电压，需要采用一定的方法获取配电台区的电压全覆盖监测或测算。

按照潮流计算方法，如牛顿法、前推回代法等[2-3]，在精确的电网拓扑参数和运行参数条件下，可以获得精确的节点电压，但方法不适应缺少无功功率或功率因数参数的低压配电网。考虑到低压配网多为家庭用户的特点，其负荷存在相似性，可通过近似计算，以召测的少数数据为基础，对其他用户电压快速作出估算。当估算值满足精度要求时，便可掌握低压用户的电压分布概况。

查阅国内外文献，目前在配电网电压估算方面，以线损估算[2-6]的研究居多，直接面向节点电压的估算仍然限制于潮流估算。由于220 V低压配网的量测装置限制，在潮流计算无法适应的情况下，本文对配电网的电压估算另辟思路，以低压配电网的可用参数为基础，通过电压降落近似计算分析了低压配电网线路电压降落的影响因素，考虑到实际采集条件对电压召测点数量的限制，使得线路的电压降落值难以获得，提出了“节点负荷矩”的概念，将节点电压与节点负荷矩相联系。通过分析节点负荷矩与节点电压的关系，联系BP神经网络的自学习能力，提出基于BP神经网络的低压配电网电压估算方法，通过召测少数节点电压，对配电台区其他节点电压进行全覆盖估算，为低压配网的电压估算提供了有效、实用的方法。

1 220 V低压配电网的参数情况

电力网络的计算中，电网参数主要包括结构参数和运行参数，对于220 V低压配电网来说，通常其架空线与电缆参数都有详细记录，且在同一台区，架空线与电缆大多都采用同一型号。

对于运行参数，由于全面的监测设施投资太大，在用户处能获得的实时运行参数很少，主要能获得以下参数：

(1)用户有功功率；

(2)首端配变电压、电流、有功功率、无功功率；

(3)少数用户电压。受采集系统限制，电压召测点数量十分有限，且以周为周期更换召测点。

值得注意的是，虽然用户的无功功率及功率因数缺失，但在低压配电网中，用户多为家庭用户，功率因数相对较高，且波动不大，有利于对电压降落进行近似计算。

2 农村低压配电网近似电压降落

220 V低压配电网的电压降落估算以首端公变二次侧作为电源节点，包括从配网首端公变二次侧到所有用户接户点间的线路电压降落计算。对于图1所示220 V低压配电网，A点代表首端配变，B、C代表接户点节点，空心圆代表用户，首端配变与接户点节点之间的连接线为低压主干线，一个配变及其下面所供电的全部用户区域称为一个台区。在已知配电台区首端配变电压和各用户功率分布的前提下，电压降落计算包括从配变二次侧，即线路首端节点A，到低压主干线的各接户点(B,C,…)间所有线路的电压降落。

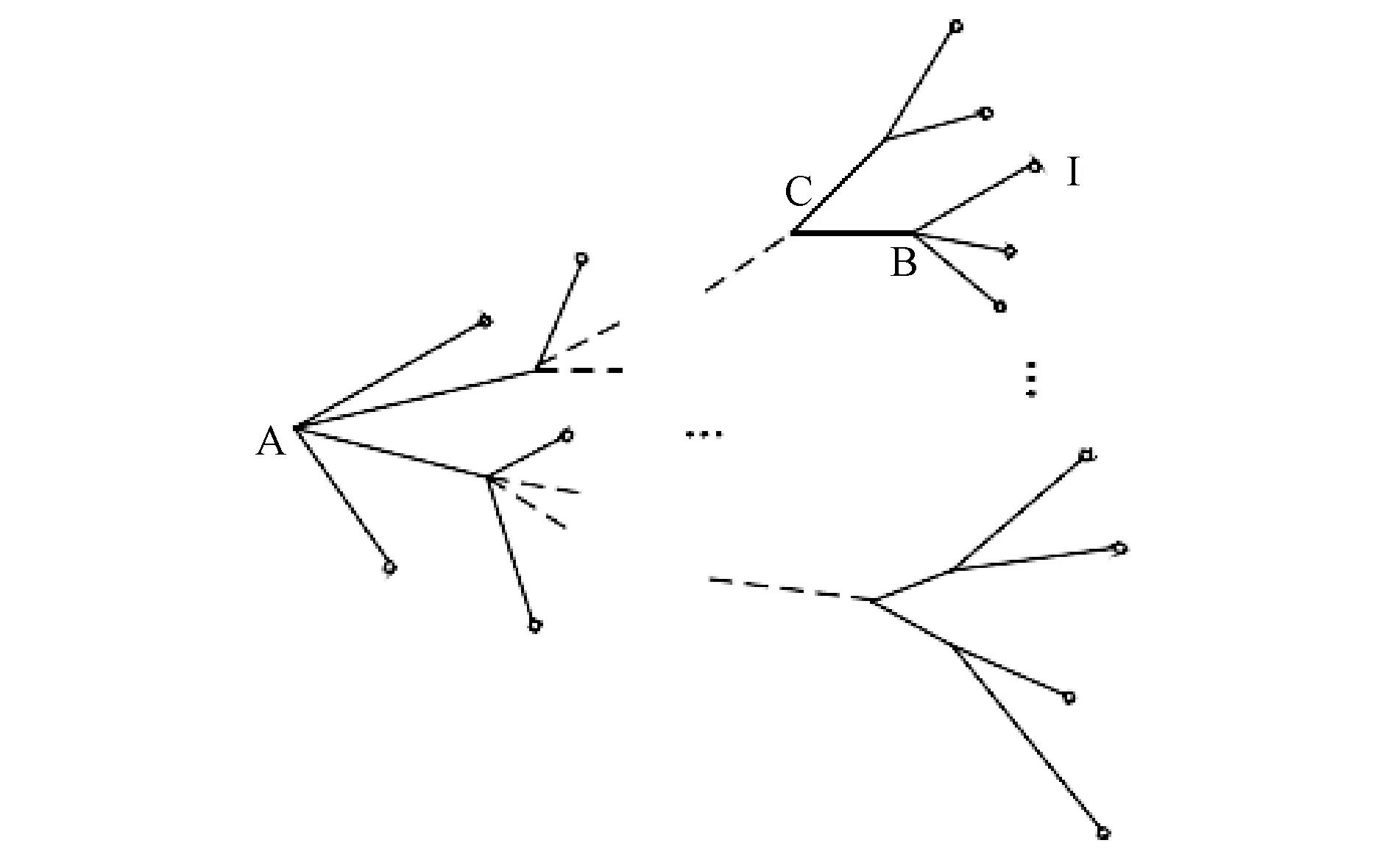
图1 低压配电网结构Fig.1 Low voltage distribution network structure

2.1架空线路电压降落近似计算

对于220 V低压配电台区，尤其是农网及城镇配网，其配电线路以架空线为主，因此本文对于电压降落及电压估算的分析以架空线路为模型。220 V配网由于电压等级不高，架空线的电容和电晕损耗可忽略不计[9]，从而架空线等效电路简化为一个串联阻抗电路，如图2所示。

图2 架空线等值电路Fig.2 Equivalent circuit for a 220 V overhead line

设首端功率为S=P+jQ，架空线等效串联阻抗产生的电压降落包含纵分量和横分量两部分，当计算只关心电压的数值时，忽略电压降落的横分量，对于电压估算可以获得足够准确的结果。故架空线串联阻抗产生的电压降落值可由纵分量近似表示为

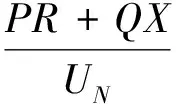
(1)

式中：L为线路长度；M为线路负荷矩，即线路上流过的功率与线路长度的乘积；R0和X0分别为线路单位电阻和单位电抗；φ为功率因数；UN为额定电压。

2.2电压降落影响因素分析

根据2.1节式(1)可知，影响一段线路电压降落的因素有线路负荷矩M、线路单位阻抗和功率因数。

(1)负荷矩

由式(1)可知，负荷矩与线路的电压降落成正比。

(2)线路单位阻抗、功率因数

设A=R0+tanφX0，线路单位阻抗取决于线路的型号，其中R0=ρ/S，ρ代表线路导线的电阻率(Ω·mm2/km)，S为导线截面积(mm2)。架空线单位电抗X0一般在0.4 Ω/km左右[2]。对于居民用户的用电负荷而言，其负荷存在相似性，功率因数值一般较高，且波动较小，取值范围大约在0.8～0.98之间[2]，从而tanφ取值范围为0.75～0.2，当X0取值在0.4左右时，功率因数和单位电抗的乘积对电压降落的影响很小，可忽略不计。

综上可知，影响架空线路电压降落值的主要因素为线路负荷矩及导线的单位电阻。线路负荷矩和单位电阻均与电压降落成正比；实际考察220 V低压配电台区的线路结构参数，若单独就某个配电台区而言，同一台区的架空线多采用同一型号，单位电阻为定值，对所有线路电压降落的影响水平相同。因此，对同一台区的不同段线路，影响其电压降落水平的主要因素为线路负荷矩。

3 低压配网的节点负荷矩及节点电压影响因素分析

3.1节点负荷矩

线路的电压降落与线路的负荷矩成正比，根据第1小节所述，实际条件中能够直接获得的参数为少数节点的电压，可计算的线路电压降落较少，甚至在某些召测情况下无法获得，而线路负荷矩并不能直观地反应与节点电压的关系，故而定义一个新的概念“节点负荷矩”。

定义1 一个节点与首端节点间的所有线路的线路负荷矩之和称为该节点的节点负荷矩。

(2)

式中:Pij为i与j节点之间线路上流过的功率;Mij为线路的负荷矩。

图3 简单低压配网拓扑Fig.3 Simple topology of low voltage power distribution network

设ξi为i节点与首节点之间线路上的所有节点的集合(i=2,3……8)，如ξ3={1,2,3}，每个节点的节点负荷矩为

(3)

式中：ML代表节点负荷矩，若j、k节点之间无线路，其线路负荷矩视为0。

由式(3)可知，节点负荷矩可视为线路负荷矩的累积，节点离首端电源节点越远，线路负荷矩累计越大，则节点负荷矩越大。

3.2节点电压影响因素分析

若从首端向后推算节点电压，某个节点与首端节点之间的电压降落为该节点与首端节点之间所有线路的电压降落之和，由于电压降落主要受线路负荷矩影响，故节点电压的大小受该节点与首端节点之间所有线路的线路负荷矩影响。根据节点负荷矩的定义，节点负荷矩是某节点与首端节点间所有线路的线路负荷矩的函数，对同一配电台区而言，节点负荷矩越大的节点，该节点前的线路负荷矩越大，所引起的电压降落值越大，节点电压越低。由此将线路负荷矩对电压降落的影响转化为节点负荷矩对节点电压的影响。在同一低压台区拓扑中，节点负荷矩水平是节点电压最直观的影响因素。

4 BP神经网络在低压配电网电压估算中的应用

4.1BP神经网络

人工神经网络是一种基于数据建模并具有自学习能力的智能算法，主要用于预测、模式识别、函数优化等数学建模。其中，BP神经网络是人工神经网络结构中最常用的一种网络结构，其工作原理在许多文献中都有详细介绍[10-14]，本文不再赘述。

一般采用具有三层神经元的BP神经网络结构，包括输入层、隐含层和输出层，如图4所示。根据实践经验，三层神经网络可以很好地模拟任何输入-输出的映射关系。

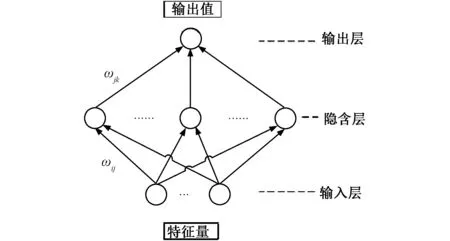
图4 BP神经网络结构图Fig.4 BP neutral network structure

4.2BP神经网络与低压配网电压估算的结合

根据第1节所述220 V低压配电网系统可获得的电网参数，结合2.2节及3.2节分析，将有功和无功功率对电压降落的映射近似转化为负荷矩与电压降落的函数映射关系。在无法采集无功功率的情况下，利用用户的有功功率分布，忽略线路损耗，根据式(2)和式(3)计算得到某一配电台区中各节点的节点负荷矩。

在同一配电台区中，不同水平的节点负荷矩必然对应不同的电压水平，但具体的映射关系是未知的。针对某一台区拓扑，构造适应该台区的节点负荷矩——电压估算模型，结合BP神经网络对未知映射关系的自学习能力，以少数节点的节点负荷矩、电压作为训练样本，训练形成的网络可模拟该台区节点负荷矩与电压的映射关系，从而以训练的网络估算台区其他节点的电压，得到电压的全覆盖估算。其中，节点负荷矩作为BP神经网络的输入特征量，节点电压为输出特征量。

4.3BP神经网络算法的改进

BP神经网络算法虽然适合配网电压估算的建模，但算法本身也不乏存在着缺点[15-17]。BP算法的误差函数E是一个具有极其复杂形状的函数曲面。算法沿着E变化最大的方向搜索最小值，在不做任何改进的情况下，只能找到极小值而不能保证找到全局最小值。若函数存在平坦区，会使权值调整后的误差变化很小，亦或陷入局部极小值而不收敛。针对以上缺点，本文在算法中添加加权因子，加权因子根据每个样本误差的大小调整其在整体误差中的比重，使得能量函数的计算处于动态调整状态。同时加权因子的加入也使学习率和动量因子随样本的比重进行动态调整，动量因子将前一次权值和阈值的调整量添加一部分到本次权值和阈值的调整量中，如果本次训练陷入局部极小值，上一次的调整量还可以使得网络走出极小值点区域，继续寻找最小值。

设算法中的加权因子为α，αm是第m对样本的加权因子，能量函数E为

根据负梯度下降理论，t时刻权值修正量为

(6)

同理，t时刻阈值的修正量与权值修正量计算方式与式(6)类似。式中：Em为第m个样本的样本误差函数，n为样本总量；Y和O分别代表实际输出和样本输出；ηm为m个样本的学习率；βm为m个样本的动量因子。

由于改进的神经网络算法中根据Em大小调整加权因子αm，Em越大，越需根据该样本作出调整，反应到αm，αm越大，从而根据式(5)调整学习率和动量因子。采用改进的BP算法，改善了网络训练中经常陷入平坦区的现象，提高了网络的训练效率。

5 算例验证

5.1样本形成

本文提取某省两个220 V低压配电台区某一日晚间19点的电压分布情况作为数据样本，选取19点时刻的运行参数是由于采集系统只能固定时间采集用户电压。由于输入和输出特征量各只有一个，对样本数量要求较少，每个台区选取7个节点数据作为训练样本，测试样本为5。图5及图6为两个台区的拓扑及选取节点位置。在选取训练样本时，为使神经网络能够更好地接近实际输入输出特性，节点负荷矩平均分布在总的节点负荷矩变化范围内。若训练样本点集中选取在根节点或源节点附近时，所训练的网络输入输出特性对其他节点的估算值相对偏低或偏高。

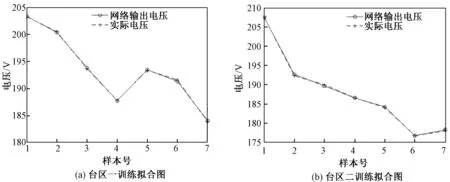
图7 BP网络训练拟合图Fig.7 BP neutral network training result

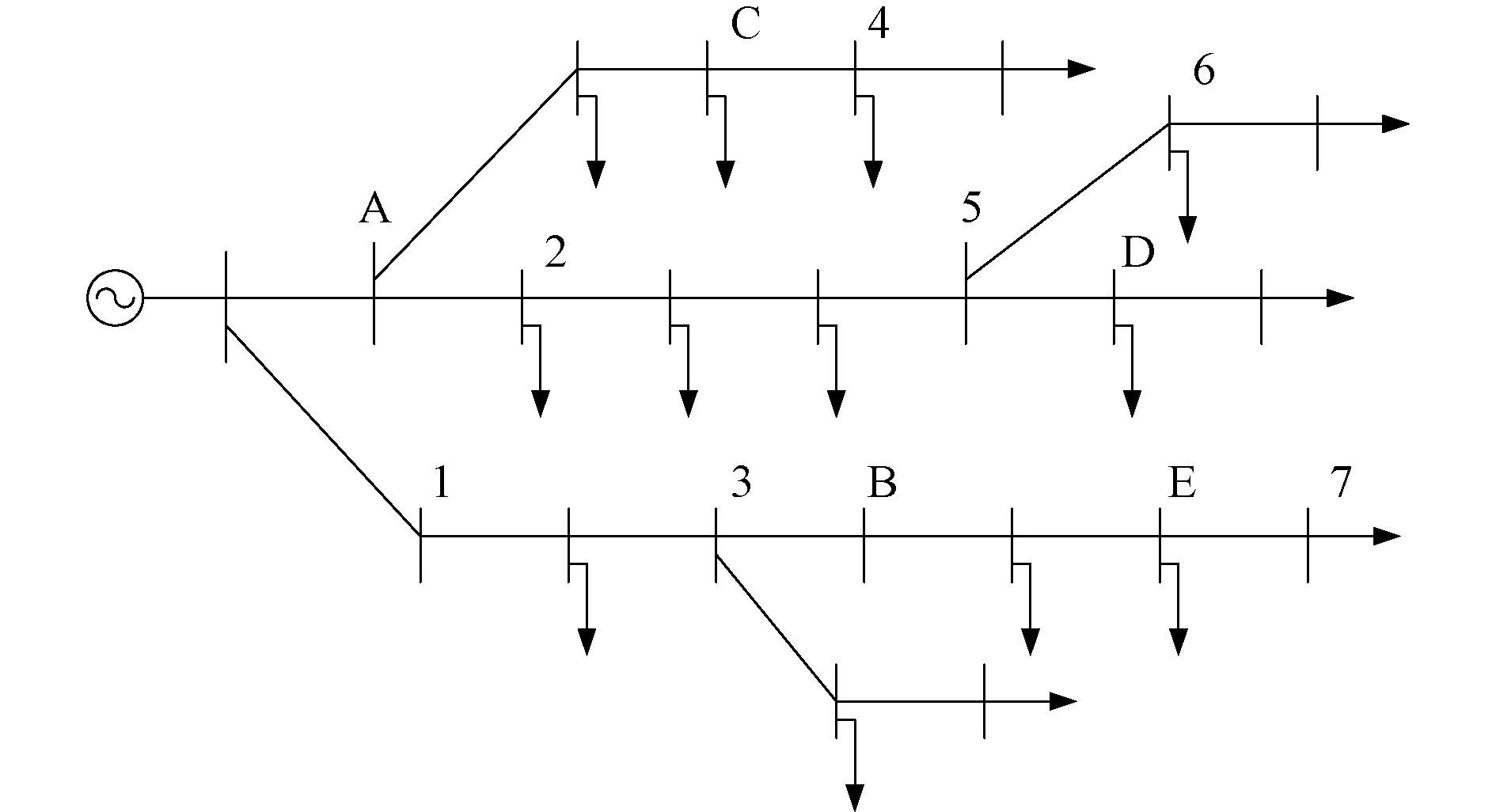
图5 台区一拓扑Fig.5 Topology for No.1 distribution network

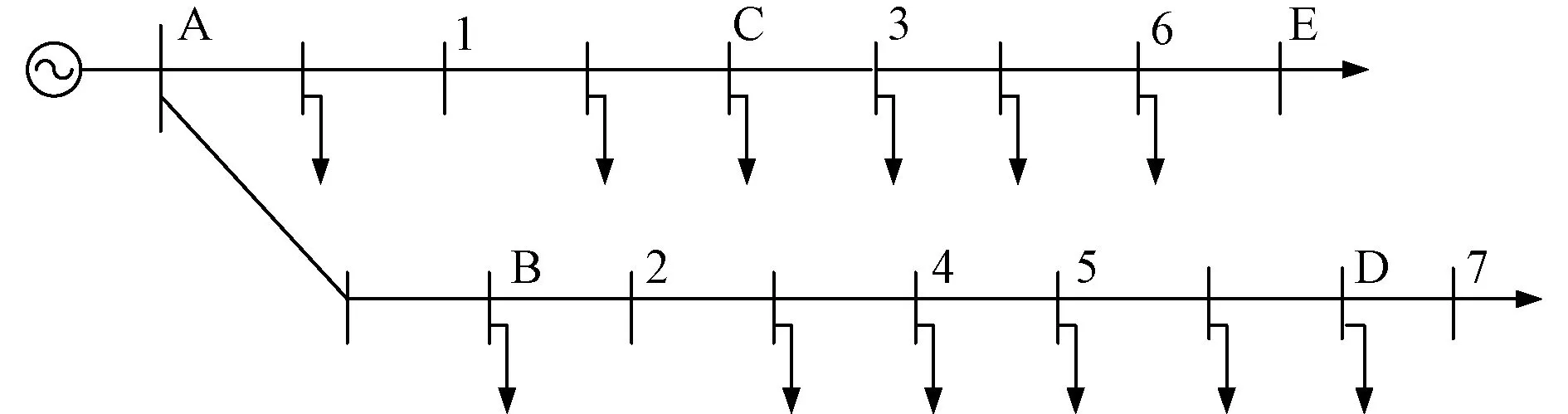
图6 台区二拓扑Fig.6 Topology for No.2 distribution network

样本数据如表1，限于篇幅，用户的功率分布及线路参数文中不予列出。

5.2神经网络训练

本文给定BP网络的训练误差为10-3，采用三层神经网络结构，输入层、隐含层、输出层的神经元数目分别为1、7、1，隐含层和输出层的激活函数为S型。为防止网络权值和阈值的初始值太大导致网络训练失效，算法中的初始值选取在(-1,1)中的随机值。由于每个台区的负荷水平不同，与电压的映射关系相应存在差异，须采用两个神经网络分别进行训练，得到的训练拟合图如图7所示。根据图7可知，BP神经网络算法对两台区的节点负荷矩与电压的映射关系拟合较好，说明训练效果优良。

表1 训练样本

为提高训练效率，本文同时采用了改进BP算法对网络进行训练，与普通BP算法的训练效果相比，误差函数的收敛速度明显提高。以台区一的训练为例，采用普通BP算法达到训练精度时的训练次数为4 756次，而采用改进BP算法达到相同的训练精度仅需要2 972次，训练速度提高了37.51%，如图8所示。

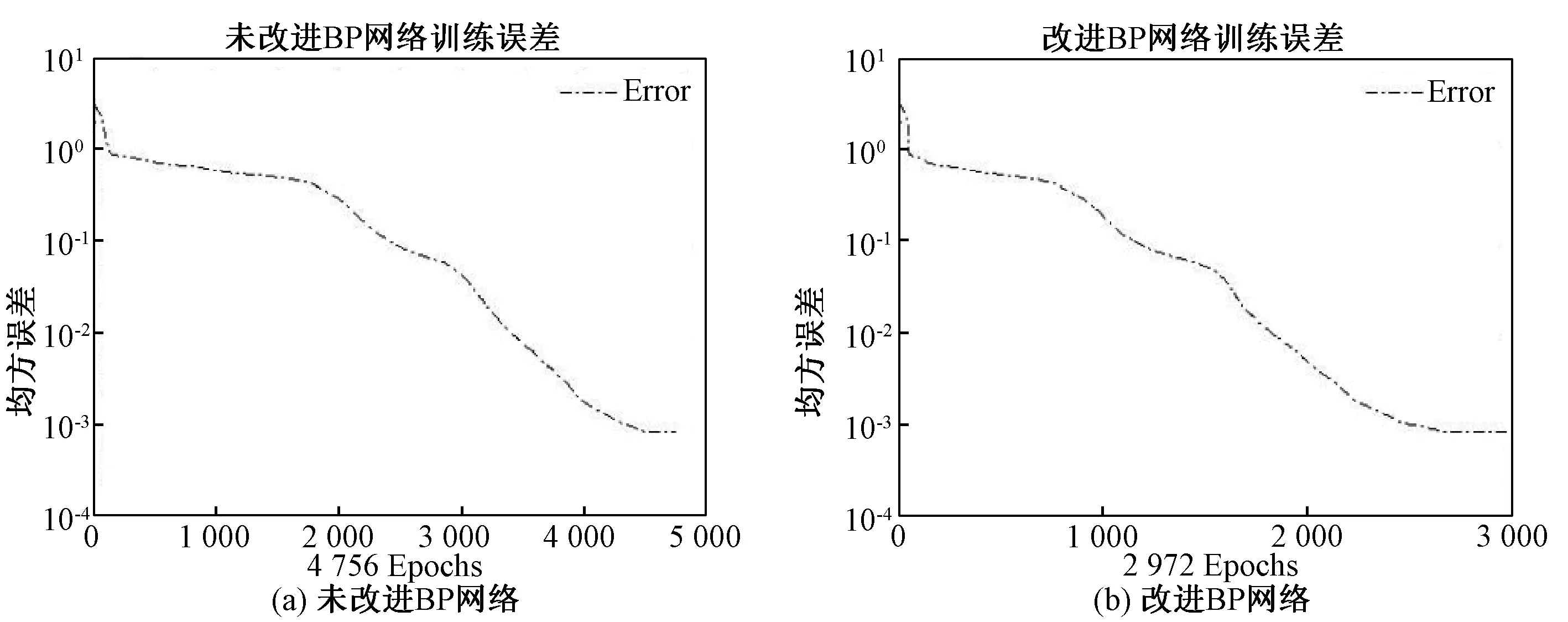
图8 BP网络训练收敛图Fig.8 BP neutral network training convergence results

5.3测试结果

训练得到的两个神经网络分别估算两个台区的测试样本的电压，得到预测结果如表2。

表2 实际电压与预测电压结果及误差

根据估算结果显示，BP网络对配电台区节点电压的估算，绝对误差控制在5 V以内，且最大相对误差在2%以下，对于通过电压估算结果掌握用户电压分布概况达到足够的估算精度要求，估算效果可观。

经过更多的配电台区电压估算实验统计，采用本文提出的配电网电压估算模型对低压配电网的用户电压进行估算，90.44%的估算结果的绝对误差控制在5 V以下，最大相对误差不超过6%，测试数据误差统计情况如表3。

根据实验验证数据可知，BP神经网络算法可以适应低压配电网的电压估算模型，在缺少大量运行参数的情况下，以少量已知的节点数据获得整个拓扑下的电压估算值。

表3 测试样本误差统计

6 结 论

本文通过对配电台区电压降落的近似计算，分析了低压台区用户电压的主要影响因素——节点负荷矩，在实际可获得的低压配电台区可用参数条件下，结合神经网络的适应性，提出基于BP神经网络的低压配网电压估算方法。实际案例证明，利用本文提出的算法对低压配电网所有节点电压进行估算，可以获得相对准确的电压估算结果，为低电压的监测和治理提供了有效的途径，大大节省因实现全覆盖监测而安装监测设备的成本，有益于电压质量治理的进行。

[1] GB/T12325-2008 电能质量供电电压允许偏差[S].

[2] 袁慧梅,郭喜庆,于海波. 中压配电网线损计算新方法[J]. 电力系统自动化, 2002, 26(11): 50-53.

[3] 彭穗,何朋亮,刘志伟,等. 基于前推回代法和牛顿拉夫逊法的配电网潮流计算[J]. 电子测试,2015,(2):52-53.

[4] 白牧可,唐巍,张璐,等. 基于BP神经网络群的中压配电网电压降落估算[J]. 电力系统保护与控制,2014,42(2):132-138.

[5] LASSO H, ASCANIO C, GUGLIA M. A model for calculating technical losses in the secondary energy distribution network[C] // Transmission & Distribution Conference and Exposition, Latin America, 2006: 1-6.

[6] 吴婷婷. 基于电力GIS的配电网线损分析的研究与实现[D].北京：华北电力大学,2016.

[7] 赵俊光,王主丁,乐欢. 中压配电网规划中馈线电气计算的估算方法[J]. 电力系统自动化, 2008, 32(16):99-102.

[8] 周卓敏,李湘华,何禹清, 等. 架空和电缆混合馈线的电压损耗快速估算[J]. 电力系统保护与控制, 2010,38(17): 169-173.

[9] 陈珩. 电力系统稳态分析[M]. 北京: 中国电力出版社,2007.

[10] 卓金武. MATLAB在数学建模中的应用[M]. 北京：北京航空航天大学出版社,2014.

[11] 李龙,魏靖,黎灿兵,等. 基于人工神经网络的负荷模型预测[J]. 电工技术学报,2015,30(8):225-230.

[12] 李佟,李军. 基于BP神经网络与马尔可夫链的污水处理厂脱氮效果模拟预测[J]. 环境科学学报,2016,36(2):576-581.

[13] 张明光, 李艳. 基于BP神经网络的下一交易日出清电价预测[J]. 电力系统保护与控制, 2009, 37(5): 18-21.

[14] 王宾,潘贞存,徐文远. 配电系统电压跌落幅值估算分析[J]. 中国电机工程学报,2005,25(13):29-34.

[15] 李亚,刘丽平,李柏青,等. 基于改进K-Means聚类和BP神经网络的台区线损率计算方法[J]. 中国电机工程学报,2016,36(17):4543-4552.

[16] 刘浩然,赵翠香,李轩,等. 一种基于改进遗传算法的神经网络优化算法研究[J]. 仪器仪表学报,2016,37(7):1573-1580.

[17] 蒋鼎国. 基于改进型BP神经网络PID控制器的温室温度控制技术[J]. 实验室研究与探索,2015,34(1):9-13.

Voltage Estimation of Low-voltage Distribution Network Based onBP Neural Network

YIN Zhongdong1, MU Kai1, JIN Yongtao2, TONG Li2, ZHAO Qicheng2

(1. School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China;2.Electric Power Research Institute of State Grid Zhejiang Electric Power Corporation, Hangzhou 310014, China)

The Limitation of monitoring system to collect operating parameters in low-voltage distribution grid makes it difficult to monitor all users’ voltage or calculate voltage accurately. Considering that a few users’ voltages are available, a new method to estimate node voltage of low voltage distribution grid is proposed on the basis of the BP neural network. This paper analyzes the factors that are relevant to the voltage level of rural low-voltage distribution network in accordance with the approximate calculation of the voltage drop and the available parameters in the low voltage distribution. Then this paper defines a new variable called node-load-moment and establishes a model of voltage estimation to low-voltage distribution grid. Given the self-learning ability of BP neural network to the in-out characteristics based on the data modeling, a new method with a few available parameters is proposed to estimate all users’ voltage of low-voltage distribution grid according to BP neural network. In addition, to avoid the error function falling into flat region and improve the learning efficiency of BP algorithm, this paper adds a weighting factor to the neural network. The weighting factor can adjust the learning rate and momentum factor in a dynamic manner. In the end, the data of pragmatic distribution grid examples are adopted to check the method and the simulation results show that the proposed method can calculate accurately which is feasible to the engineering application.

low-voltage distribution network; node-load-moment; BP neural network; voltage estimation; dynamic adjustment of error

10.3969/j.ISSN.1007-2691.2017.05.04

TM76

A

1007-2691(2017)05-0027-07

2016-11-13.

国家重点研发计划专项基金资助项目(2016YFB0101900).

尹忠东(1967-)，男，教授，研究方向为电力系统分析与控制、电网电能质量等；牟锴(1993-)，女，硕士研究生，研究方向为配电网电能质量。