一种消除杆臂挠曲运动影响的传递对准方法*

鲁 浩,王进达,李群生,2,程海彬,位晓峰

(1 中国空空导弹研究院,河南洛阳 471009; 2 北京航空航天大学,北京 100061)

一种消除杆臂挠曲运动影响的传递对准方法*

鲁 浩1,王进达1,李群生1,2,程海彬1,位晓峰1

(1 中国空空导弹研究院,河南洛阳 471009; 2 北京航空航天大学,北京 100061)

正确消除飞行器杆臂挠曲运动的不利影响是提高惯导系统传递对准性能的关键技术之一。文中在继承速度积分匹配方法优点的基础上,提出一种平均速度匹配传递对准方案,能够有效降低杆臂的挠曲运动对速度匹配传递对准精度和滤波稳定性的影响。通过在线计算滤波器的系统噪声矩阵Q,避免了飞行器杆臂挠曲运动建模的问题。系统仿真结果表明,该传递对准方案能够提高滤波器的稳定性,并对杆臂挠曲运动进行有效抑制。

传递对准;杆臂挠曲运动;平均速度匹配;自适应滤波

0 引言

飞行器的杆臂在气动载荷、湍流的作用下会引发挠曲运动,从而严重影响飞行载体精确制导武器中捷联惯导系统对准的精度[1-2]。国内外学者关于飞行器杆臂挠曲运动的处理方法主要分为三类[3-5]:一是建立挠曲运动的模型,该方法受飞行器的类型、飞行条件、参数以及载荷等诸多因素的影响,精确度无法保证;二是根据试验数据建立统计模型,该种方法需要对各种载体做大量的试验,需耗费大量人力、物力、财力,也是不可取的[6];三是改进滤波算法以消除杆臂挠曲运动,这种方法一般通过滤波器中注入白噪声替代杆臂变形噪声,实施简便,但由于不能充分考虑挠曲运动噪声特性而导致对准精度不高[7]。

对此,文中从两方面进行处理:1)在速度匹配中利用前置信息处理器对匹配速度进行平均化处理,以降低飞行器的杆臂挠曲运动对滤波精度的影响;2)利用子惯导系统的惯性传感器实时测量挂弹点处随机角运动和随线运动的强度,自适应调整滤波器的系统噪声矩阵Q,从而真实反映杆臂挠曲运动,提高传递对准滤波器的稳定性。

1 飞行器杆臂挠曲运动的特点

图1 挠曲运动分析模型

飞行器杆臂的挠曲运动是影响捷联惯导系统传递对准精度和滤波稳定性的一个关键因素[8-9]。从图1挠曲运动分析模型可以看出,对于战术飞行器来说,其机型不同、挂点位置多以及飞行环境的变化都会造成杆臂的随机振动强度发生变化。杆臂挠曲运动特性如图2所示,图2(a)、图2(b)分别为战术飞行器上一段典型的弹性加速度响应曲线和弹性加速度频率响应曲线,由扰动所造成的杆臂结构振动通常在5～10 Hz之间[10]。常规杆臂挠曲运动模型是由白噪声驱动的二阶马尔科夫过程来描述的[11],但这种单一的Gauss-Markov模型并不能准确描述由多个扰动源所造成的复合扰动。因此,文中仿真中采用3个二阶马尔科夫过程的混合叠加作用,来模拟杆臂随机挠性运动对传递对准精度的影响,其参数可按实验数据选择,这样既能全面描述弹性变形的干扰来源,又能保持原有的计算复杂度。其数学模型如下:

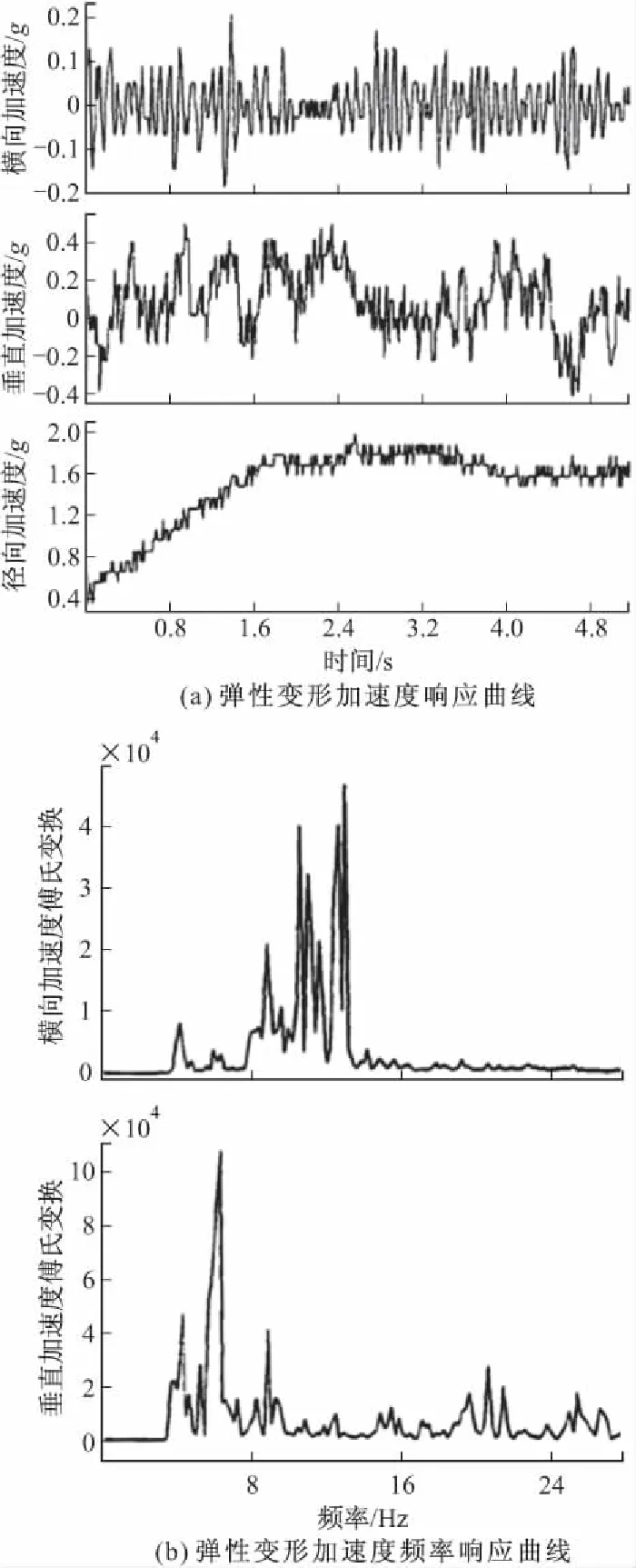
图2 杆臂挠曲运动特性

(1)

式中:

(2)

λi=λi1+λi2+λi3,λi1、λi2、λi3分别为i轴上3个干扰源的二阶马尔科夫随机量。其均方差分别为σi1、σi2、σi3,取值通常根据实验验证得到。ωi为i轴上动态挠曲变形角速率,ζ为白噪声,且ζi～N(0,Qi),μ为不规则系数,即相关时间的倒数;b2=μ2+a2,a为弹性变形的频率,D为弹性变形幅值。

2 对准方案的优选

传递对准方案中速度匹配方案对挠曲运动相对比较敏感,但对准的快速性比较好。美国在JDAM的传递对准设计中考虑到多种飞行载体挂机的通用性,在速度匹配和速度积分匹配两种方法之间进行了权衡,选择了速度积分匹配方法[9]。速度积分匹配方法对挠曲运动所造成的影响有比较好的平滑作用,从而提高传递对准滤波器的性能,相对速度匹配法而言在状态变量中增加了速度积分量δRn,但导致了对准算法计算量和对准时间的增加。

针对这种情况,可采用一种“平均速度”匹配方案,利用前置信息处理器对速度测量值进行平均化处理,如图3所示。

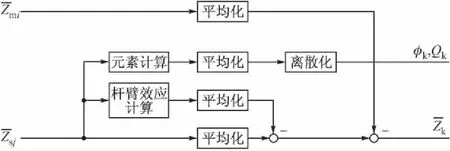
图3 前置信息处理器原理框图

“平均速度”的计算方案利用了“速度积分”的概念,通过位置量测的差ZP,得到平均速度量测量ZVaver。这种平均速度匹配方案一方面能够减小量测噪声,使挠曲运动参数得到有效的平滑,继承了速度积分匹配方案对杆臂挠曲运动敏感度低的优点,而且保持了速度匹配方案计算量小和对准快速性好的特点。

3 对准滤波器设计

在传递对准的最优滤波器设计中,如果用三阶Gauss-Markov过程来表示飞行器的杆臂挠曲运动,需要18个状态变量才能描述完整的挠曲运动模型[10-11],由此会导致计算量指数级的增加,在弹载计算资源有限的条件下不宜采用。

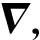
式中:ΔOa、ΔOg分别为加计和陀螺的非正交矩阵。

在对准时间比较短时,滤波器对主要惯性仪表误差的估计效果只有初始值的20%左右。若要想进一步提高其估计能力,除选择合适的机动飞行轨迹外,还应适当延长对准时间,即使是低成本惯性器件,其本身的仪表误差也需要一定的时间才能对ΔVn和Δφn产生影响。因此,在精确制导武器传递对准滤波器的状态方程中,可通过删除具有较低可观测性的仪表误差参数来降低滤波器的阶次。将仪表误差及其它状态变量作为噪声处理。降阶处理如下:

即取状态变量为ΔVn、Δφn,这样滤波器只有6阶,大大降低了计算量。在无法准确获取状态变量初值的情况下,可选取额定值较大的先验协方差值,以使滤波器对系统模型误差的变动不敏感。系统量测为主、子惯导的3个平均速度分量的差。系统状态方程和量测方程如下所示:

(3)

4 滤波参数优化

在很多实际系统中,系统噪声方差阵Q是事前未知的,在模型不准确的情况下进行滤波,常常会引起滤波器发散。采用常用的Sage-Husa自适应滤波算法[12]和强跟踪卡尔曼滤波算法[6]一方面计算量大、实时性和稳定性难以保证;另一方面降低了滤波精度。

由于系统状态噪声Q的强度与杆臂挠曲运动的状态有关[13],其取值涉及到滤波参数的优化问题。文中对系统噪声方差阵Q计算的主要思路是采用弹上惯导系统的惯性传感器实时测量挂弹点处杆臂随机角运动和线运动的强度,利用速度增量和角度增量计算Q阵,分别计算出Q矩阵中包含与速度测量相关的系统噪声值和与角度测量相关的系统噪声值。从而反映出载体在飞行状态下挂点处杆臂的挠曲运动,确保了弹上惯导系统在传递对准时适应不同的飞行器和挂点。

4.1 与速度测量相关的系统噪声QV的计算方法

不考虑加速度计零位偏差的影响[14],QV的计算可根据载体线运动和挂弹点杆臂挠曲运动的变化而变化,从而保证滤波器系统噪声矩阵的准确性,其模型如下:

QV=diag[k1·(|ΔVx|2+|ΔVy|2+|ΔVz|2)]

(4)

式中:ΔVi为i轴速度增量;k1是正比例系数。

4.2 与角度测量相关的系统噪声QU的计算方法

QU与子惯导系统在每一个滤波步长时角增量和滤波步长有关,即[15]:

(5)

式中:Δθi为i轴角度增量;TKF为滤波步长;k2和k3是比例系数。

从式(5)中可以看出,影响QU数值大小与陀螺的非线性和陀螺的零位漂移有关。QU与时间的关系(漂移影响)必须根据方位通道在没有机动或机动很小的要求来选择。与QV类似,QU与载体的角运动的大小和挂弹处杆臂角振动时刻相关,从而确保了卡尔曼滤波器系统噪声QU的准确性。

5 仿真分析

5.1 仿真条件

仿真设置的初始条件为[16]:初始失准角φx=40′,φy=70′,φz=30′;陀螺漂移ε=3.3°/h(1σ),刻度因子误差Kg=2×10-4(1σ);加速度计偏置=5×10-4g(1σ),刻度因子误差Ka=5×10-4(1σ);初始速度为300 m/s,在0～10 s内水平直线飞行,在10～50 s内进行转弯机动,机动过载分别为1g、2g和3g。

5.2 杆臂挠曲运动仿真模型

杆臂挠曲运动可以认为是由几个独立频率随机运动的叠加而成。根据式(1)、式(2),得到杆臂挠曲运动参数见表1,其中x、y和z分别表示杆臂3个方向的随机振动,数字1、2和3表示每个轴向的3个二阶马尔科夫过程的参数。

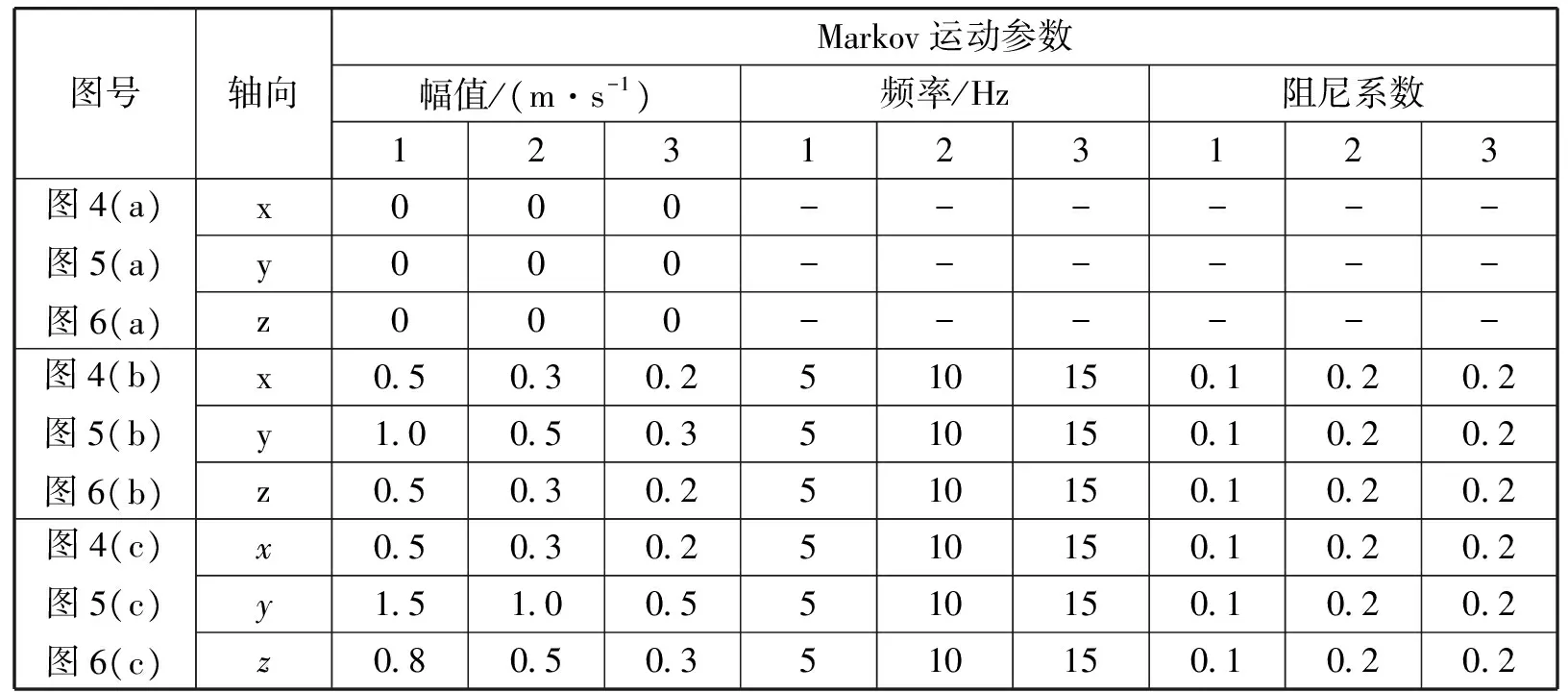
表1 杆臂挠曲运动参数

图4 1 g转弯机动飞行时杆臂挠曲运动的影响

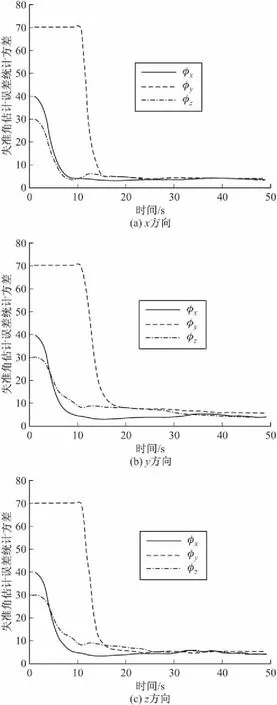
图5 2 g转弯机动飞行时杆臂挠曲运动的影响

5.3 仿真结果

从表1和图4～图6可以看出,杆臂的y轴和z轴挠曲运动的强度逐步增强。方位失准角φx受杆臂随挠曲运动的影响小;φz的收敛时间随y轴和z轴挠曲运动的强度逐步增强有一定的延长,但在10 s后稳定在10′以内,35 s后基本稳定在5′左右;杆臂随挠曲运动对φy的估计影响比较小,在10～50 s时间段内,随着转弯加速度的增大(1～3g),φy的收敛时间变短,很快降到10′以内,逐步稳定到5′左右。仿真结果表明,平均速度匹配传递对准方法对杆臂挠性运动能够有效抑制,且滤波器工作性能稳定,无发散现象。

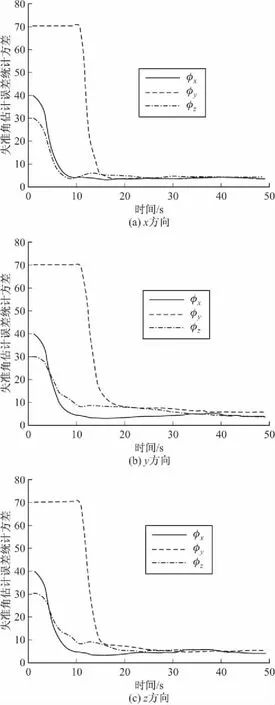
图6 3 g转弯机动飞行时杆臂挠曲运动的影响

6 结论

针对惯导系统传递对准中飞行器杆臂挠曲运动难以建模的问题,文中提出了一种新的传递对准方案。该方案首先在继承速度积分匹配方法优点的基础上,扩展了速度积分的概念,提出了平均速度匹配方案,然后利用精确制导武器弹上惯性传感器实时在线测试杆臂随机的角运动和线运动,对滤波噪声矩阵Q进行实时计算。采用Monte Carlo法对所提传递对准方案的滤波效果进行仿真,仿真结果表明平均速度传递对准方案能够有效抑制载体杆臂弹性对传递对准的不利影响,滤波器工作性能稳定,鲁棒性好。

[1] 王司,邓正隆.惯导系统动基座传递对准技术综述 [J].中国惯性技术学报,2003,11(2):61-67.

[2] 朱绍箕.惯导系统动基座对准技术评述 [J].战术导弹控制技术,2004(3):46-49.

[3] 鲁浩,杜毅民,王纪南.应用于近距空空导弹惯导系统的传递对准技术 [J].中国惯性技术学报,2005,13(5):10-15.

[4] 管叙军,王新龙.捷联惯导系统动基座传递对准匹配方法 [J].航空兵器,2014(2):3-8.

[5] 房建成,张舟,宫晓琳.机载分布式POS传递对准建模与仿真 [J].中国惯性技术学报,2012,20(4):379-385.

[6] GROVES P D.Optimising the transfer alignment of weapon INS [J].The Journal of Navigation,2003,56(2):323-335.

[7] KLOTZ H A,DERBAK C B.GPS-aided navigation and unaided navigation on the joint direct attack munition [C] ∥ IEEE 1998 Position Location and Navigation Symposium.[S.l.:s.n.]，1998.

[8] 解春明,赵剡,王纪南.传递对准中机翼弹性变形建模与滤波处理 [J].北京航空航天大学学报,2010,36(8):931-935.

[9] 肖艳霞,张洪钺.考虑机翼弹性变形时的传递对准方法研究 [J].航天控制,2001,19(2):27-35.

[10] HAVINGA M C,Flight test results of a MEMS IMU based transfer alignment algorithm for short range air-to-air missiles:AIAA 2013-5244 [R].2013.

[11] MOCHALOV A V,KAZANTSEV A V.Use of the ring laser units for measurement of moving object deformations[A]∥Second International Conference on Lasers for Measurement and Information Transfer.2002.

[12] AKPAN V A， HASSAPIS G.Adaptive predictive control using recurrent neural network identification [C]∥17th Mediterranean Conference on Control and Automation,2009:61-66.

[13] 徐晓苏,邹海军,刘义亭,等.基于鲁棒滤波的挠性变形和动态杆臂补偿算法 [J].中国惯性技术学报,2015,2(1):9-12

[14] KAIN J E,CLOUTIER J R.Rapid transfer alignment for tactical weapon applications:AIAA 89-3581-CP [R].1989.

[15] 解春明,赵剡,杨传春.传递对准滤波中机翼变形噪声的在线补偿算法 [J].系统工程与电子技术,2011,33(2):370-375.

[16] 孔星炜,董景新,郭美凤.速度与角速度双积分匹配传递对准 [J].清华大学学报(自然科学版),2011,51(4):443-447.

AMethodofTransferAlignmenttoRemovetheInfluenceofLever-armFlexure

LU Hao1,WANG Jinda1,LI Qunsheng1,2,CHENG Haibin1,WEI Xiaofeng1

(1 China Airborne Missile Academy,Henan Luoyang 471009,China; 2 Beijing University of Aeronautics and Astronautics,Beijing 100061,China)

One of the key to the question of improving the performance of transfer alignment was to remove the negative influence of lever-arm flexure correctly.A project of transfer alignment about average velocity matching was proposed to reduce the influence to the accuracy of transfer alignment and the stability of filters effectively,which inherited the advantage of the method about velocity-integral matching.A method of real-time calculating system-noise-matrixQwas proposed,which avoided the problem of modeling the lever-arm flexure.Simulation results demonstrated that the transfer alignment scheme could increase the stability of Kalman filter,and could also inhibit the influence of the lever-arm flexure effectively.

transfer alignment; lever-arm flexure; average velocity matching; adaptive filtering

10.15892/j.cnki.djzdxb.2017.02.011

2016-04-05

鲁浩(1963-),男,陕西西安人,研究员,研究方向:惯性导航技术。

V249.3

A