霍尔推力器仿真与优化*

丛云天，陈 健

(北京控制工程研究所，北京 100190)

*总装预研基金资助项目(9140A20050315HT05002).

霍尔推力器仿真与优化*

丛云天，陈 健

(北京控制工程研究所，北京 100190)

针对霍尔推力器通道内的放电过程，建立一种基于COMSOL软件的仿真模型.该模型以等离子体内部电子和离子的漂移扩散为核心，结合电磁场、气体流动以及等离子体内部的碰撞反应，通过合理选取系统方程、边界条件以及求解器，有效估算霍尔推力器的性能参数以及各物理量在通道内的分布.将仿真结果与理论相比较，验证该模型用于霍尔推力器数值仿真的有效性并以此对推力器进行磁场优化设计.

霍尔推力器；等离子体；漂移扩散；有限元

0 引 言

霍尔推力器(Hall effect thrust，HET)自20世纪70年代在前苏联流星号卫星上应用以来，经过几十年的发展日趋成熟，出现了多款经典的飞行产品，如SPT-100、PPS-1350G、BPT-4000等.霍尔推力器由空心阴极、放电室、磁场生成器(内/外磁线圈、磁极)以及阳极/气体分配器等结构组成.霍尔推力器的工作原理如图1所示，内外磁线圈在环形通道内产生径向磁场，阳阴极之间的放电等离子体在通道内将产生自洽的轴向电场.阴极发射的部分电子在流向阳极过程中遇到正交的径向磁场与轴向的电场将形成E×B漂移(霍尔漂移).推进剂通常采用惰性气体氙(Xe)或氪(Kr)，从阳极/气体分配器注入推力器通道，同做漂移运动的电子发生碰撞并被电离，离子在轴向电场的作用下加速喷出产生反冲推力，同时电子通过传导机制到达阳极，在通道内实现稳定的等离子放电过程，提供持续稳定的推力[1].

国外针对霍尔推力器的仿真建模已开展了大量研究，结合网格粒子仿真(particle in cell，PIC)、蒙特卡洛(MCC)或直接蒙特卡洛碰撞法(DSMC)等方法对放电室工作过程、壁面溅射腐蚀和羽流发散进行仿真，并构建了较为成熟的仿真代码或程序，如HPHall(Hybrid-PIC Hall)、PICPluS3D等[2-3].

本文采用有限元分析软件COMSOL Multiphysics对霍尔推力器放电通道建模仿真，对比分析1.5 kW 级霍尔推力器的数值仿真结果，验证软件和数值模拟方法的可行性.在此基础上，进一步提出推力器的优化设计.

1 物理数学模型

考虑到霍尔推力器放电室工作机理，对推力器内部等离子体性质的求解主要基于COMSOL软件的直流放电模块，该模块引用一种新型的等离子体模拟混合模型，既具有流体模型的较快计算速度同时又适用于低压等离子体模拟.此外，COMSOL适用于对等离子体动力学、推进剂、电磁场进行耦合计算.根据推力器放电过程的主要工作机理，采用合理的系统方程或控制方程描述等离子体内部反应机制以及各粒子的迁移输运性质.

1.1系统方程

1.1.1 电子扩散

对于电子的运动，近似采用漂移扩散模型由电子数密度和平均电子能量来描述，通过求解电子连续性方程和能量守恒方程得到[4].

电子连续性方程为：

(1)

电子能量守恒方程计算电子能量密度：

(2)

式中，nε为电子能量密度，Rε为由于非弹性碰撞引起的能量损失或增加项，με为张量形式的电子能量迁移率，Dε为电子能量迁移率.

考虑到漂移扩散方程固有的高度非线性，电子数密度在阳极附近等离子体鞘层区域内很短的距离上就有10个数量级的跨度；在鞘层区域内离子同电子的迁移率和扩散性存在较大的差异，这种差异将形成一个与空间带电隔离区，在此区域内形成了一个能够明显提高电子能量的强电场区域.为解决这些问题，仿真中采用直接求解电子数密度和电子能量密度的对数[5].

存在磁场情况下，真实的电子迁移率的表达式不能用一个简单的形式来表达，而应该采用张量形式的电子迁移率

(3)

式中μdc为无外加磁场时的电子迁移率.

电子的扩散系数、能量迁移率、能量扩散系数分别为

(4)

式中，Te为电子温度，定义Te=2nε/3ne.

1.1.2 重物质扩散

对于非电子粒子(重物质)，采用扩散输运方程，假设计算中有k(k=1,…，Q)种类型物质的流体以及j(j=1,…，N)种反应类型，那么输运方程可表示为[5]：

(5)

式中，Jk为扩散通量矢量，Rk为k种离子的比率表达式，u是中性粒子速度矢量，ρ是混合成分的密度，wk是第k种离子的质量分数.

扩散通量矢量Jk为

Jk=ρwkVk

(6)

Vk是k种成分总的扩散速度矢量，采用混合平均模型计算，在Maxwell-Stefan公式基础上进行简化，混合平均公式保留了质量守恒定律且计算量较小，对扩散系数Dk的简化表达便于计算，但计算精度下降[6].Vk可表示为

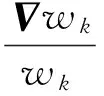
(7)

(8)

而混合平均迁移率可通过爱因斯坦关系式计算

(9)

式中，q是单位电荷，kB为玻尔兹曼常数.

1.1.3 磁场

J=σV×B+Je

(10)

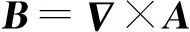
(11)

其中，A为磁势矢量，M为磁化强度矢量

1.1.4 N-S方程

(12)

式中，ρ为密度，u为速度矢量，P为压强，F是体积力矢量，τ是粘性应力张量，S是应变率张量，μ是动态粘度.

1.2化学反应

霍尔推力器通道内部等离子体的粒子组成成分包括电子、离子和中性粒子(激发态和基态)，气体放电的本质是带电粒子与中性原子、激发态原子的相互碰撞，以及这些粒子与壁面之间的相互碰撞.电离主要发生在靠近推力器放电通道出口的电离区，中性气体到达电离区后与高速运动的电子发生碰撞，当电子的能量高于中性气体的电离能时，中性气体可能发生电离.因为推力器中电子能量较低，高能电子碰撞电离很少发生，而低能电子与中性气体碰撞后所生成的离子在加速电场的作用下喷出，所以二次电离很少发生，通常认为推进剂电离后主要生成一价离子.

上述全部反应可归为两大类：①弹性碰撞，即粒子碰撞只改变运动方向而粒子的总动量和动能均守恒，粒子本身能量未改变且无新的粒子或光子产生；②非弹性碰撞，碰撞过程引起了粒子内能变换，或伴随着新的粒子以及光子的产生[6].碰撞反应的反应速率由相应的碰撞截面与电子能量分布函数(EEDF)进行积分得到.霍尔推力器等离子体瞬态放电过程近似为平衡态系统的放电，则EEDF可取为麦克斯韦(Maxwell)分布函数.而氙碰撞截面可根据Szabo[7]以经验数据给出的分段函数计算.

1.3边界条件

在霍尔推力器仿真过程中，COMSOL软件在直流放电模块和层流模块中的边界条件设置尤为重要，对仿真结果具有较大影响，需根据实际工况和理论进行合理设置和选择.

1.3.1 电子壁边界条件

等离子体区域的壁面条件包括二次电子发射和热发射.为表征等离子体中非电子类粒子的传输特性，将放电空间内的固体边界进行边界反应设置.其主要的反应包括在所有的等离子体放电空间固体边界处均发生激发态氙原子和氙离子复原为基态原子的反应.而后者正是产生二次电子的反应，该电子对于推力器通道内放电过程尤为重要，正是由于轰击产生的二次电子不断地补充放电通道内的电子损失，维持整个放电过程，因而应设置边界处的二次电子发射系数[5].

在电子的漂移扩散过程中，对于放电空间内的固体边界要外加“壁”边界条件.该种边界条件主要用来描述电子在遇到固体边界时产生电子密度变化的各种情况，其采用的电子交换机理是电子的损失取决于扩散到边界处的等离子体中的净电子流量、在电子平均自由程内与边界条件的碰撞；电子密度的增加则取决于边界处由于正离子的轰击而引起的二次电子发射或边界的热发射(阴极).在壁上电子通量的法向分量方程以及电子能量密度的方程为：

(13)

其中，r是反射系数(一般情况下为0)，ve,th为热运动速度，γp是由离子引起的二次电子发射系数，Γp是离子通量，Γt是热发射通量，εp是发射电子的平均能量，ε为平均热离子能，n是向外的法线方向.热运动速度ve,th定义为：

(14)

1.3.2 层流边界条件

等离子体内部流动采用可压缩层流计算，相对于稳定的固体壁，层流在边界上的速度均为u=0.因此，模型计算中采用无滑移壁.入口处应用质量流边界条件，出口处一般通过法向应力条件规定，给定出口的压力边界条件求解内部速度.

1.4物理模型

针对1.5 kW级磁聚焦型(ATON)霍尔推力器进行二维轴对称建模，其简化后的几何尺寸结构参见图2.完整的霍尔推力器包括阳极、阴极、气体分配器、通道套筒及磁路等，这里阴极简化为出口平面处的边界，并给定热发射电子通量.在模型中设置各部分的材料，阳极采用1Cr18Ni9Ti，磁路选择非线性磁性材料，励磁线圈采用Cu，陶瓷套筒采用六方氮化硼(BN).

对于物理场的选择，考虑层流模块、磁场模块以及直流放电模块，根据霍尔推力器内部反应的机理选择相应几何区域，并设置相应的系统方程、化学反应和边界条件及其相关参数.之后对仿真区域进行网格划分，在等离子体放电区、近阳极区和出口处采用较为细化的网格，其他仅有磁场的区域可适当划分.最终计算区域的网格划分如图3所示.

2 计算结果分析

2.1性能参数

霍尔推力器仿真采用COMSOL 5.2.0.166版本，仿真电脑采用Intel(R) Core(TM) i5-4570 CPU，主频3.2 GHz，安装内存(RAM)16 GB，64位操作系统.

对于1.5 kW级霍尔推力器，选取放电电压和电流分别为368 V和3.7 A，阳极气体标准流率为4.2 mg/s，计算初始条件为电子密度为1×1014m-3，初始平均电子能量为4 V.理论计算结果为：功率1 361.6 W、推力95.6 mN、比冲2 317 s.通过采用之前所描述的模型，可以模拟获得的磁场、粒子数密度、电势等主要参数的空间分布.

霍尔推力器等离子通道内磁场线分布及通道中轴处磁场强度沿轴向分布见图4.由图可见，中轴线上磁场有正负梯度的变化，并且在轴线两侧的磁场逐渐增强，形成一个不均匀的鞍形磁场分布，这与ATON型霍尔推力器的凸向阳极的磁场形状设计相符.中轴线上，磁场强度最大值位于磁极端面处，约为248.42 Gauss；最小值位于z=42.2 mm处，约为25.53 Gauss，使得在近阳极区磁场强度较弱，有利于减小阳极加速电压损失.

霍尔推力器通道内电子的传导决定了电势的分布，进而影响工质的电离和加速.从图5中可以看出，推力器内电势降分布主要集中在推力器通道出口附近，在缓冲区及和缓冲区相接的区域电势变化不明显.而从通道内轴线上的电势分布可得，电势在

z=54 mm之后逐渐下降，即可以得出放电通道加速区的长度.

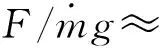
2.2电离过程分析

通过COMSOL对放电通道的仿真，可记录0～1 s 内通道内部电子或离子数密度的变化情况(见图7)，即电离过程.图8为不同时刻的推力器通道中轴线上离子数密度分布.在放电初期(t=10-6s)，放电集中于通道出口处，而随着电子与原子发生碰撞电离，离子数密度逐渐增加.同时，电子发生霍尔漂移，向阳极方向传导维持等离子体放电，因此离子数密度继续升高，在近阳极区域由碰撞产生的离子数也逐渐增大.由于离子在加速段向推力器出口运动，故在近出口处离子数密度最大.放电至10-4s后保持稳定，此后推力器内部离子数密度分布基本不变.目前离子数密度的仿真计算结果为：在氙气气量为4.2 mg/s、电压为368 V条件下，推力器通道内离子数密度最高为2.53×1019m-3，达到预期的电离效果.

3 优化设计

在验证已有推力器主要性能参数与模型计算结果相符的基础上，进行优化设计分析.对于给定功率与放电通道宽度的推力器，主要通过优化磁场位形、改善磁聚焦特性等方法.

3.1磁聚焦

在ATON型霍尔推力器中，附加磁线圈的引入产生凸向阳极的磁场形状，使离子流聚集到通道的中心，减少了离子壁面损失和离子束的羽流发散损失.若弯曲程度过小可能无法达到聚焦离子的效果，而弯曲程度过大则有可能出现过渡聚焦现象，即离子可能从一个壁面沿径向迁移而运动到另一个壁面，同样会造成壁面腐蚀、性能下降[8].因而，磁力线的弯曲程度需要进一步优化设计，使得聚焦效果最好.

在保持通道中轴线处磁场强度几乎不变的条件下，调整磁场磁力线与通道中心线的关系，设计3种典型的磁场位形(见图9)，比较推力器的性能.在氙气气量为4.2 mg/s、电压为368 V条件下，比较3种磁场位形下推力器通道内的参数(见图10)：聚焦型磁场的性能最佳，通道内离子数密度最高为2.63×1019m-3，出口离子速度为22 371 m/s，相应比冲为2 283 s，接近理论计算值.此外，电离区的离子分布显示出聚焦磁场不仅可提高出口速度，还可提高电离率以及中心区域的离子密度.

因此，在霍尔推力器设计时，应设计聚焦型磁场，有利于减小等离子体的发散和对内外壁面的侵蚀作用，以及提高比冲.

3.2磁屏设计

ATON将推力器中心磁铁分为两部分设计，降低了放电通道前部的磁场强度，即形成靠近阳极的零磁场区，使得磁场向通道后部聚集，形成出口处的大梯度磁场区.为了降低通道前半部分的磁场强度及调节通道内的磁场形状，还须进行磁屏设计.外磁线圈产生的部分磁场通过与外磁屏及外围空气形成的局部回路而损失掉，同理，内磁屏也消耗了部分内磁线圈产生的磁场[9].在建立的模型中考虑在内线圈靠近进气区域放置磁屏，采用高饱和、耐腐蚀的铁铝软磁合金.

加入磁屏后放电通道中轴线上磁场强度分布如图11所示.磁屏的加入使得通道前半部分的磁场强度明显降低，近阳极区域的磁场强度降至6.83 Gauss，有利于抑制电子对阳极电极的侵蚀；同时，磁极端面处最大场强相对提高.此时通道内离子数密度的分布如图12所示，等离子体整体电离度改变较小，但受磁场影响更易于约束在放电中心区域内.相比无磁屏设计，等离子中心区域的分布比例较高，靠近壁面的数量较少.同时，磁聚焦中心区域离子受电场加速作用，出口离子速度进一步增大，达到25 167 m/s，此时比冲为2 568 s.

4 结 论

对于霍尔推力器放电过程的二维仿真计算，本文利用COMSOL有限元分析软件建立模型进行仿真，可对推力器的磁场、电场以及等离子体的分布与性能参数进行合理预测.在此基础上，通过改进磁场聚焦性能和磁屏设计，可改进原有推力器的性能.

[1] GOEBELD M, KATZ I. Fundamentals of electric propulsion: ion and Hall thrusters[M]. John Wiley & Sons, 2008.

[2] GAMERO-CASTANO M, KATZ I. Estimation of Hall thruster erosion using HPHall[M]. Pasadena, CA: Jet Propulsion Laboratory, National Aeronautics and Space Administration, 2005.

[3] VICINI A, PASSARO A, BIAGIONI L. Hall thruster 3D plume modeling and comparison with SMART-1 flight data[J]. European Space Agency, 2004：555.

[4] HAGELAARG J M， PITCHFORD L C. Solving the boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models[J]. Plasma Sources Science and Technology,2005(14):722-733.

[5] CHRISTOU A G. Modeling of an electrical propulsion system: towards a hybrid system[R]. Royal Military College of Canada, 2015.

[6] DAVIDB. Go. Gaseous ionization and ion transport: an introduction to gas discharges[D]. Cambridge: University of Notre Dame, 2012

[7] SZABO Jr J J. Fully kinetic numerical modeling of a plasma thruster[D]. Cambridge: Massachusetts Institute of Technology, 2001.

[8] 于达仁，刘辉，丁永杰,等. 空间电推进原理[M].哈尔滨：哈尔滨工业大学出版社，2014.

[9] 潘海林，丁凤林，李永等. 空间推进[M].西安：西北工业大学出版社，2016.

SimulationandOptimizationofHallEffectThruster

CONG Yuntian, CHEN Jian

(BeijingInstituteofControlEngineering，Beijing100190，China)

Based on COMSOL soft, a method is established to model the discharge processing in Hall effect thruster (HET) channel. The drift diffusion of electron and ion of the plasma is taken as the kernel of the model. Combined with the electromagnetic field, flow and impact reactions inside plasma， the characteristics of HET and distribution of parameters in the channel can be evaluated with proper selection of equations, boundary conditions and solvers. Compared with the results in theory, numerical simulation results demonstrate the effectiveness of the proposed approach， and then the magnetic field optimization design is applied.

HET； plasma； drift diffusion； finity

2016-12-08

V439

A

1674-1579(2017)05-0061-07

10.3969/j.issn.1674-1579.2017.05.010

丛云天(1993—)，男，助理工程师，研究方向为电推进技术；陈健(1969—)，男，研究员，研究方向为推进技术.