基于规范的牺牲阳极阴极保护优化设计方法
2019-08-28尚世超张维毅
李 璐 尚世超 郭 宇 张维毅
(中国船舶及海洋工程设计研究院 上海200011)
引 言
海洋中的钢质结构物会受到海水严重的腐蚀作用,需要采取必要的防腐措施[1]。海洋工程进行防腐设计时,综合考虑水下涂层的耐久性、维修难度和经济性,固定式、长寿命海洋平台全浸区的结构多不采用涂层保护,仅依靠阴极保护来防止腐蚀破坏。相比外加电流阴极保护方法,牺牲阳极阴极保护方法因其技术可靠和不需要后期维护等优势而被广泛采用。牺牲阳极阴极保护设计通常采用DNV RP B401推荐的初期、平均和终期保护电流校核的方法或者NACE SP 0176推荐的Design slope方法[2]。DNV RP B401推荐的方法中几乎没有给出具体的优化指导,NACE SP 0176推荐的方法中也只是对牺牲阳极设计给出了方向性的指导。正是因为缺乏具体的设计和优化指导,即便相同基本设计条件也会有多种完全不同的牺牲阳极阴极保护方案,难以对其优劣进行评估。因此,建立无涂层海洋结构物的牺牲阳极阴极保护方案优化方法是非常必要的。
1 牺牲阳极阴极保护方案设计参数及指标
牺牲阳极阴极保护方案的基本参数包括阴极保护系统设计寿命T、受保护面积Ac、海水电阻率ρ等,设计参数包括牺牲阳极的其形状尺寸和材料等[3]。牺牲阳极材料根据使用环境即可确认,其形状尺寸则是通过长度、宽度和高度来确认[4]。为按照牺牲阳极的细长程度和截面扁平程度进行系列化的分析,引入了牺牲阳极细长系数和扁平系数的定义。牺牲阳极细长系数Cl和扁平系Cf数定义如式(1)~(2)所示。

式中:La为牺牲阳极长度,m;r为牺牲阳极截面等效半径,m,r=C/2π,C为截面周长;Ba为牺牲阳极截面上、下边长度的算术平均数,m;Ha为牺牲阳极截面高度,m。
牺牲阳极长度确定后,通过细长系数即可确认截面等效半径,进而通过扁平系数确认截面尺寸。牺牲阳极细长系数和扁平系数代替牺牲阳极截面宽度和高度来定义牺牲阳极。利用牺牲阳极长度、细长系数和扁平系数更易体现牺牲阳极尺寸和形状这些设计参数对方案优劣的影响。
牺牲阳极阴极保护方案优劣的评判指标包括牺牲阳极总数量Na和牺牲阳极总质量Ma。若假定牺牲阳极保护电流分布效率为100%,牺牲阳极总数量越少则安装工作量越少;在能保证阴极保护效果的情况下,牺牲阳极总质量越小则所需费用越多少。因此,所需牺牲阳极总数量少、总质量小的方案更优。
2 牺牲阳极阴极保护方案设计参数与指标关系
2.1 牺牲阳极接水电阻公式整理
单块牺牲阳极质量ma可表示为式(3)所示形式[3]:
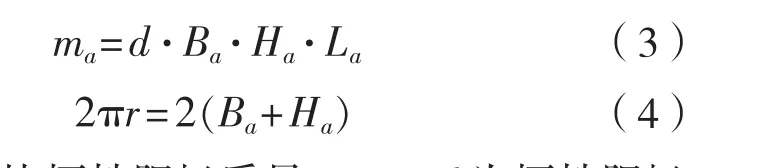
式中:ma为单块牺牲阳极质量,kg;d为牺牲阳极材料密度,kg/m3。
根据式(1)~(2),式 (4),Ha、Ba可表示为:
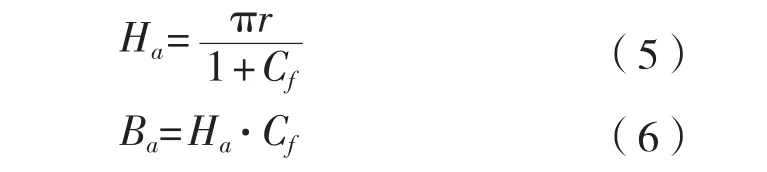
根据式(3),(5)~(6),单块牺牲阳极质量ma可表示如式(7)所示形式。
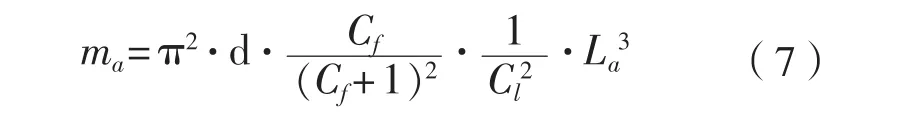
根据规范以及式(1)~(2),式(5)~(6),海洋工程中较多采用Slender stand-off型和Long flush-mounted型牺牲阳极[5],其接水电阻计算公式可分别表示为式(8)~(9)所示形式。
Long slender stand-off型:
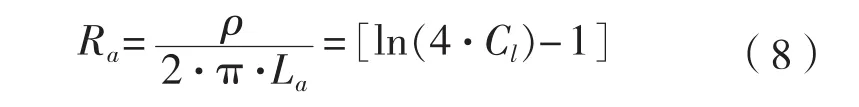
Long flush-mounted型:
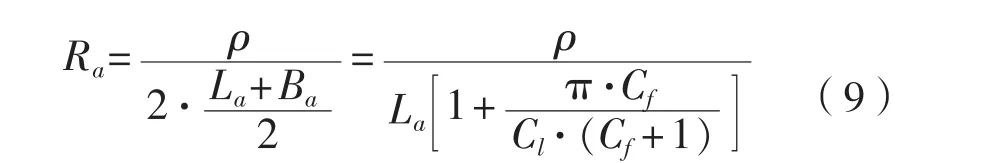
式中:Ra为接水电阻,Ω。
所需牺牲阳极总数量和牺牲阳极材料总质量如式(6)~(7)所示[6]。

式中:Ac为受保护面积,m2;S为 Design slope,Ω·m2;ma为牺牲阳极总质量,kg。
通过式(3)~(11)可以建立单块牺牲阳极设计参数(长度La、细长系数Cl和扁平系数Cf)和设计指标(总数量Na和总质量Ma)之间的关系,依据牺牲阳极类型进行具体分析。
2.2 Long slender stand-off型牺牲阳极
将式(3)和式(8)代入式(10)~(11)整理可得式(12)~(13)。
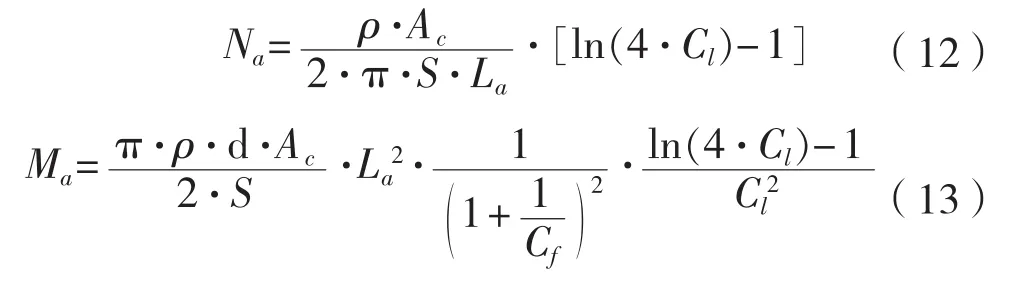
式(12)和式(13)分别给出了Long slender stand-off型牺牲阳极时,总数量和总质量与单块牺牲阳极尺寸和形状之间的关系。分析函数的单调性,可以得到如下规律:
(1)当牺牲阳极的细长系数不变时,总数量会随牺牲阳极长度的增长而减少;
(2)当牺牲阳极的长度不变时,总数量会随着牺牲阳极细长系数的增大而增多;
(3)当牺牲阳极细长系数和扁平系数不变时,总质量会随着牺牲阳极长度增长而增大;
(4)当牺牲阳极长度和扁平系数不变时,总质量会随着细长系数增大而减小;
(5)当牺牲阳极长度和细长系数不变时,总质量会随着扁平系数增加而增大。
为结合具体数据,表1列出了几种海洋工程中常用的Long slender stand-off型牺牲阳极型号及其长度、细长系数和扁平系数。
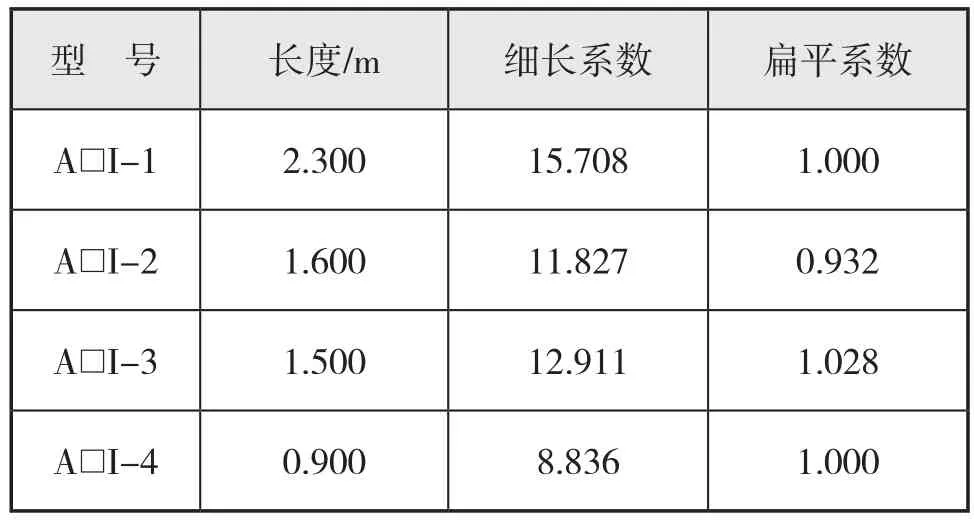
表1 海洋工程常用Long slender stand-off型牺牲阳极型号及形状尺寸
表1中列出的牺牲阳极的扁平系数都接近或者等于1,这与管状铁芯匹配。因此,Long slender stand-off型牺牲阳极设计时可直接选取扁平系数Cf为1,式(13)也可简化为如式(14)所示的形式。
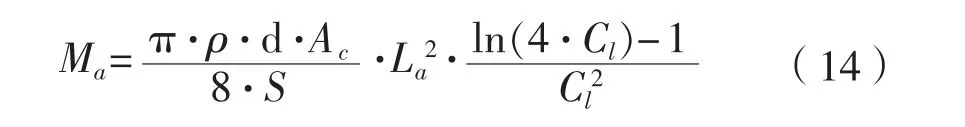
选择某一基本参数工况:设计寿命为20年;海水电阻率为0.25 Ω·m;平均保护电流密度和终期保护电流密度都为32 mA/m2;保护面积为1 000 m2;设计斜率为3.5 Ω·m2;牺牲阳极驱动电压为0.25 V;牺牲阳极材料密度为2 750 kg/m3;牺牲阳极材料消耗速率为3.8 kg/(A·y)。参照表1取牺牲阳极长度范围为0.8~2.5 m,细长系数范围为8.0~20.0,按式(12)和式(14)可分别计算并绘制牺牲阳极长度、细长系数与牺牲阳极总数量和总质量的三维关系图,如图1所示。

图1 牺牲阳极设计参数与指标关系图
关系图得到的结论与上文通过函数单调性的分析相同。这是因为当牺牲阳极长度越长、形状越粗短时,牺牲阳极体积越大,因而接水电阻越小,单块牺牲阳极输出电流能力越强。特定环境下结构物所需的保护电流是一定的,随着单块牺牲阳极输出电流能力增加,需要的牺牲阳极数量随之减少。牺牲阳极质量的增加速度相对接水电阻减少速度更快,即增加牺牲阳极电流输出量是以增加更多的牺牲阳极质量为代价的。所以,牺牲阳极长度越长、形状越粗短,会需要更多的牺牲阳极材料。
因此,当所需牺牲阳极总数量很少时其总质量则会很大,其总质量很小时其总数量则会很多。图2给出了归一化的牺牲阳极总数量和总质量的关系。
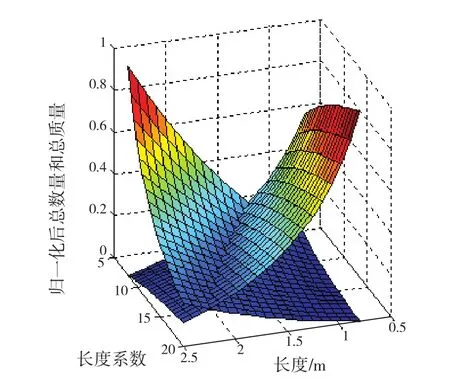
图2 归一化的牺牲阳极总数量和总质量关系
2.3 Long flush-mounted型牺牲阳极
将式(3)和式(9)代入式(10)~(11),整理可得式(15)~(16)。
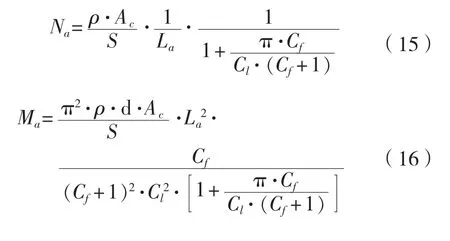
式(15)和式(16)分别给出了Long flushmounted型牺牲阳极时,总数量和总质量与单块牺牲阳极尺寸和形状之间的关系。分析函数的单调性可以得到如下规律:
(1)当细长系数和扁平系数不变时,牺牲阳极总数量会随着长度增加而减少;
(2)当长度和扁平系数不变时,牺牲阳极总数量会随着细长系数增大而增多;
(3)当长度和细长系数不变时,牺牲阳极总数量会随着扁平系数增大而减少;
(4)当细长系数和扁平系数不变时,牺牲阳极总质量会随着长度增加而增大;
(5)当长度和扁平系数不变时,牺牲阳极总质量会随着细长系数增大而减小;
(6)当长度和细长系数不变时,牺牲阳极总质量会随着扁平系数增大而减小;
表2列出了几种海洋工程中常用的Long flushmounted型牺牲阳极型号及其长度、细长系数和扁平系数。
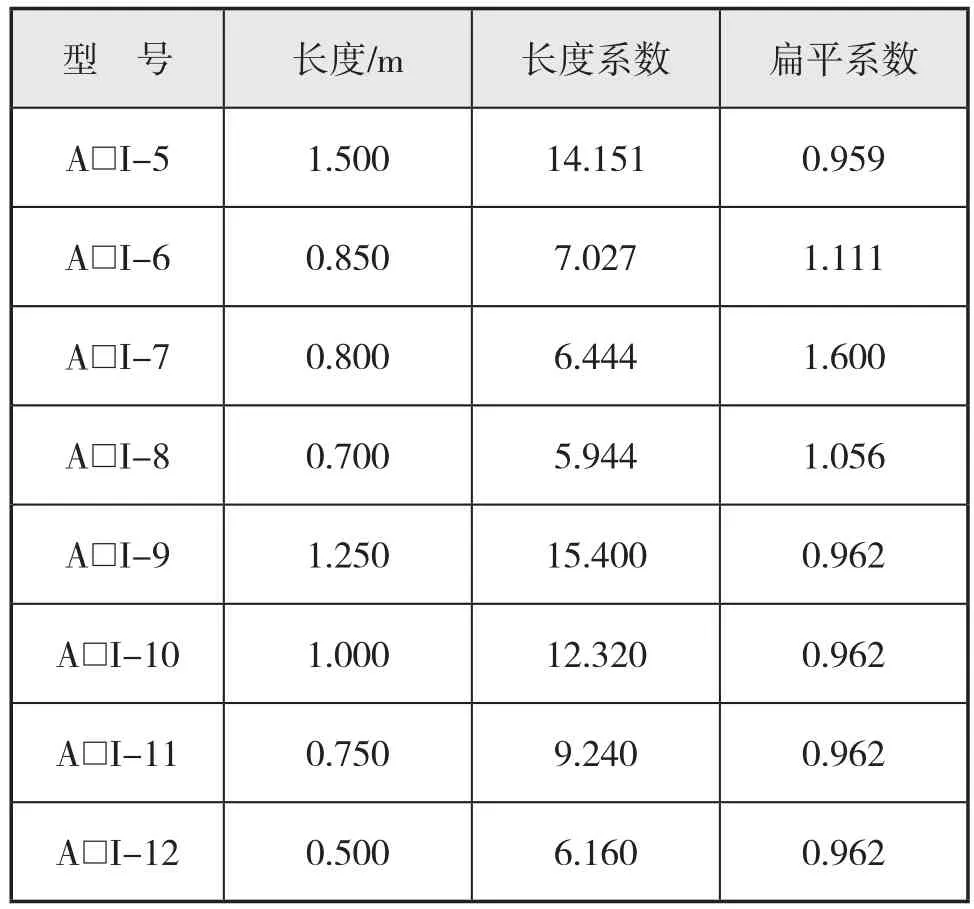
表2 海洋工程常用Long flush-mounted型牺牲阳极型号及形状尺寸
表2中列出的牺牲阳极除A□I-7型号外,其他型号的扁平系数接近于1。据此,可将式(15)~(16)化简为如式(17)~(18)所示形式。
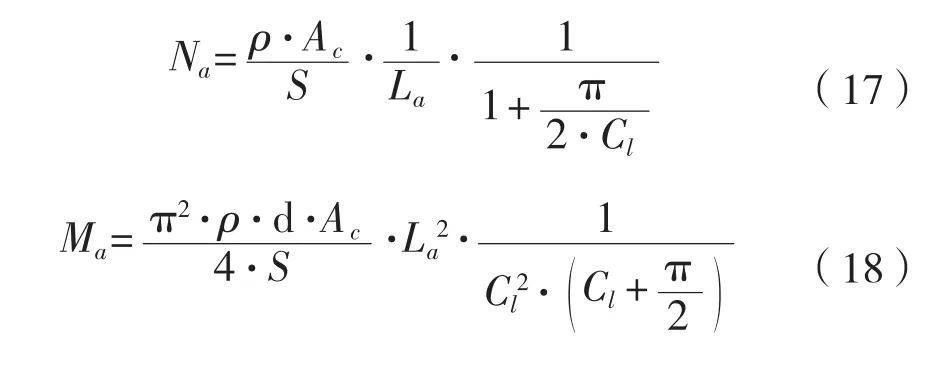
仍选用上组基本参数工况,令牺牲阳极长度范围为0.4~2.6 m,长度系数范围为4.0~16.0,按式(17)和式(18)可分别计算绘制牺牲阳极长度、长度系数与总数量和总质量的三维关系图,如图3所示。
Long flush-mounted型牺牲阳极结论及原因与Long slender stand-off型牺牲阳极基本相同。图4给出了归一化的牺牲阳极总数量和总质量的关系。

图3 牺牲阳极设计参数与指标关系图
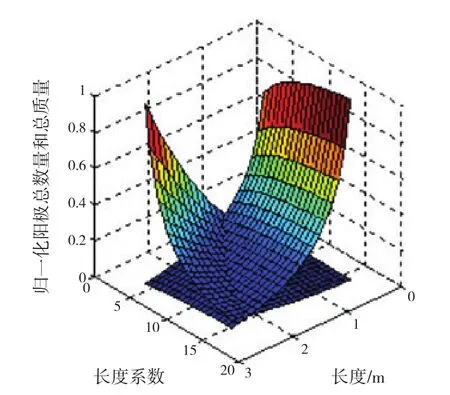
图4 归一化的牺牲阳极总数量和总质量关系
3 牺牲阳极阴极保护方案优化问题模型及解法
3.1 牺牲阳极阴极保护方案优化问题模型
牺牲阳极长度越长需要的布置空间越大,尤其是在型材较多和板材弧度较大的部位,牺牲阳极的布置工作量也会大大增加。铁芯在牺牲阳极截面中的位置对其实际利用率有很大的影响,其应在牺牲阳极材料消耗将尽时仍能提供足够的支持能力,保证牺牲阳极不因材料发生脱落而过早失效[7]。牺牲阳极截面尺寸越小或越扁平,铁芯的布置位置和截面形状设计难度越大。因此,牺牲阳极的长度、细长系数和扁平系数都应限制在一定范围内,以保证其能够方便布置安装和具有较高的实际利用率,如式(19)所示。
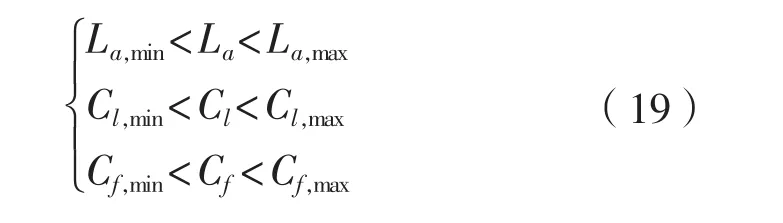
选取牺牲阳极长度、细长系数和扁平系数范围时,可用参考常用牺牲阳极或者根据结构物的具体情况确定。
除了牺牲阳极的长度、细长系数和扁平系数的范围限制外,牺牲阳极还需满足材料消耗的要求,如式(20)所示。

式中:im为维护电流密度,A/m2;T为设计寿命,y;k为牺牲阳极消耗速率,kg/(A·y)。
根据Design slope定义,式(20)可整理为式(21)所示形式。
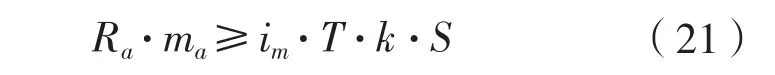
规范推荐的Design slope值足够小,能满足结构物初期的极化的要求。所以,式(21)同时反映了初期极化要求和材料消耗要求。将式(3),(8)~(9)代入式(21),可以得到Long slender stand-off型和Long flush-mounted型牺牲阳极的初期极化要求和材料消耗要求,分别如式(22)和式(23)所示。
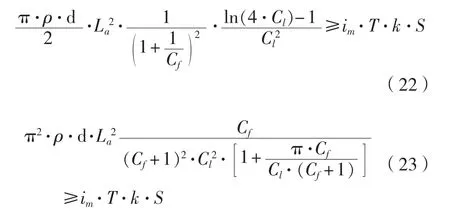
按照规范,当牺牲阳极在终期消耗至其利用率时,假定Long stand-off型牺牲阳极截面为圆形,Long flush-mounted型阳极截面为半圆形,即此两型牺牲阳极的扁平系数分别为1.0和0.5。两型牺牲阳极的长度可认为不变,而将其截面有效半径减少90%,所以此两型牺牲阳极终期长度系数如式(24)所示。牺牲阳极质量与铁芯关系可参照规范确定。
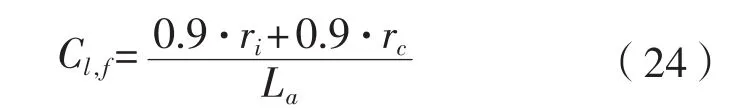
式中:ri为牺牲阳极截面初期等效半径,m;rc为牺牲阳极铁芯等效板,m。
为保证结构物在设计终期能够被足够极化,应满足如式(25)所示条件。

式中:Sf为终期Design slope,Ω·m2;为驱动电压,一般取为0.25 V;if为终期保护电流密度,mA/m2。
结合Design slope定义,式(25)可转化为式(26)所示形式。

式中:Ra,f:单块牺牲阳极终期电阻,Ω。
将式(8)~(9)代入式(26),得到 Long slender stand-off型和Long flush-mounted型牺牲阳极在终期需满足的极化条件表达式,如式(27)~(28)所示。

因此,只有长度、细长系数和扁平系数满足式(19)、式(22)(或式(23))以及式(27)(或式(28))的牺牲阳极,才会使结构物在整个寿命期内得到足够的极化和有效的阴极保护。
前文分析表明,牺牲阳极总数量和总质量之间存在相互制约的关系,减少其中一个量则会以牺牲另外一个量为代价:多数量的牺牲阳极会增加安装的费用,但会减少牺牲阳极材料的费用;较少数量的牺牲阳极会减少安装费用,但会增加牺牲阳极材料的费用。虽然牺牲阳极总数量和总质量之间不可同时取得最优值,但两者却都可以用费用来统一度量。
若假定牺牲阳极材料费用与其质量近似成线性关系,则材料费可用式(29)表示。

式中:Pm为牺牲阳极材料费用,万元;λ1为牺牲阳极材料单价,万元/kg。
若假定安装牺牲阳极总需要一定的基本费用,且安装费用会随牺牲阳极数量增加近似成线性增加,则牺牲阳极安装的费用可用式(30)表示。

式中:Pn为牺牲阳极安装费用,万元;λ2为牺牲阳极安装单价,万元/块;P0为牺牲阳极基础安装费用,万元。
因此,牺牲阳极阴极保护方案所需的总费用可用式(31)表示。
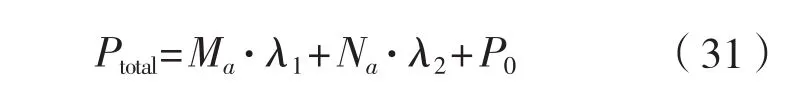
引入指标E,使其满足式(32)所示条件。

式中:f1为数值与牺牲阳极材料总质量相同,万元;
f
2为数值与牺牲阳极总数量相同,万元;c1为系数,;c2为系数
E值并不表示真正的方案费用,只是表示方案优劣的评判指标,E值越小方案越优。这样处理的好处是可以将有量纲的单价化为无量纲的权重,简化计算分析。
综上所述,式(19)、(21)、(25)以及式(32)构成了牺牲阳极阴极保护方案优化问题模型,如式(33)所示。
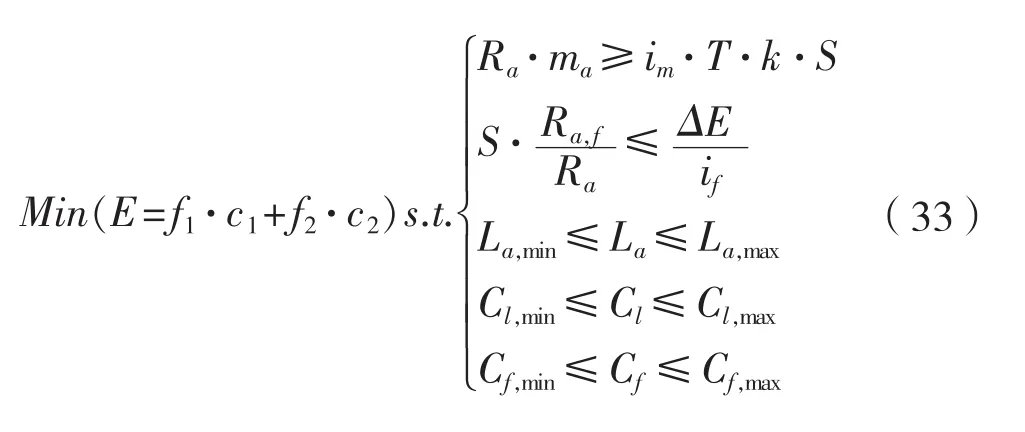
3.2 牺牲阳极阴极保护方案优化问题解法
理论上满足式(33)限制条件的牺牲阳极长度、细长系数和扁平系数有无数种组合,但考虑实际工程设计精度就只有有限的组合了。因此,只要按照工程设计精度将牺牲阳极长度、细长系数和扁平系数的范围进行划分,得到有限的设计参数组合,然后遍历这些设计参数组合,找出符合极化要求和材料消耗要求的设计参数组合,选取其E值最小的组合,即为经济性最优的设计方案。具体的解法如图5所示。
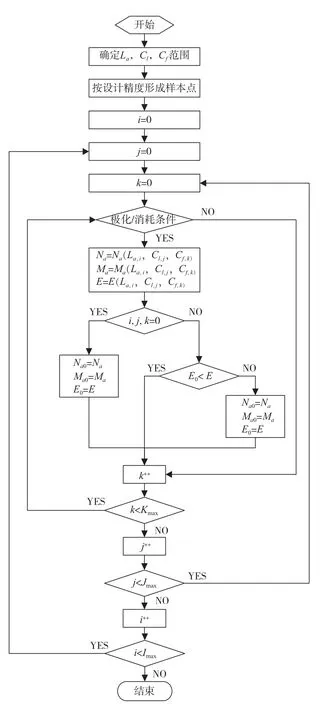
图5 牺牲阳极阴极保护方案优化问题解法
4 结 语
本文提出了细长系数和扁平系数的概念,可以看出牺牲阳极的长度越长、形状越短粗,所需牺牲阳极材料更多。所需牺牲阳极总数量很少时,总质量会很大;牺牲阳极总质量很小时,总数量则会很多。
牺牲阳极的长度、细长系数和扁平系数都应限制在一定范围内,以保证其能够方便布置安装和具有较高的实际利用率。
牺牲阳极总数量和总质量之间存在相互制约的关系:多数量的牺牲阳极会增加安装的费用,但会减少牺牲阳极材料的费用;较少数量的牺牲阳极会减少安装费用,但会增加牺牲阳极材料的费用。引入E值,用于评判方案的优劣,将有量纲的单价化为无量纲的权重,提出E值越小、方案越优,简化计算分析。
