考虑负载切换的超声加工振动建模与控制

张建国，隆志力，李祚华，邹建军，杨宇辉

（1.哈尔滨工业大学（深圳）机电工程与自动化学院，广东深圳 518055；2.东莞理工学院机械工程学院，广东东莞523808）

考虑负载切换的超声加工振动建模与控制

张建国1，隆志力1，李祚华1，邹建军2，杨宇辉2

（1.哈尔滨工业大学（深圳）机电工程与自动化学院，广东深圳 518055；2.东莞理工学院机械工程学院，广东东莞523808）

通过建立换能器和负载的等效M-C-K数学模型，分析了负载对超声波换能器的动态影响，并在Matlab软件中建立换能器的传递函数与仿真模型。提出了PID和H∞振动控制算法，其是建立在Matlab的Simulink仿真。通过对比分析发现，PID和H∞算法可实现准确、快速的控制效果。最后，对理论和仿真计算进行了实验验证。

超声波换能器；负载切换；振动控制器；超声辅助加工

近年来，随着蓝宝石、陶瓷、碳纤维等材料的应用，传统加工方法已出现加工效率低、性能差等劣势，而超声加工技术在新材料特别是硬脆材料的加工方面具有广泛的应用前景[1-3]。在超声加工中，必须保证超声波换能器具有较高的机电转换效率，故需使超声波换能器工作在谐振状态。由于复杂的环境（如温度变化）及不同材料的谐振频率，会使超声波换能器在加工过程中随时间变化[4-5]，且不同的材料加工需要不同的振动功率，这就需要精确控制驱动超声波功率。因此，超声波系统及其控制是材料去除系统中的关键组成部分，直接决定了材料的去除效率、刀具寿命和可靠性。

虽然国内外学者对超声振动切削加工技术给予了极大的关注，但传统的研究大多在空载条件下进行，其结果只能片面地反映系统的性能，故在实际加工过程中，结合负载一起进行研究极具现实意义[6-7]。目前，推广超声加工的关键问题是超声振动的自适应控制及发展。本文通过建立一个数学等效换能器M-C-K模型，论证了在有负载的情况下，对超声波换能器动态特性的影响，并在Matlab软件中进行换能器的传递函数分析、计算及建立仿真模型。同时，提出了PID振动控制算法，研究发现，PID算法可实现准确、快速的控制效果。最后，对理论和仿真计算进行了相关的实验验证。

1 超声波换能器机械结构

如图1所示，超声辅助加工的超声波换能器由锁相环的超声波发生器、压电驱动器、前盖板、锥形喇叭杆和加工工具组成。压电驱动器产生的超声波振动能量通过喇叭杆和刀具传递到工件上，能在工件上形成超声波振动效应。超声波换能器的参数为工作频率60 kHz、超声波功率500 W。超声加工模型见图2。

图1 超声辅助加工的换能器结构示意图

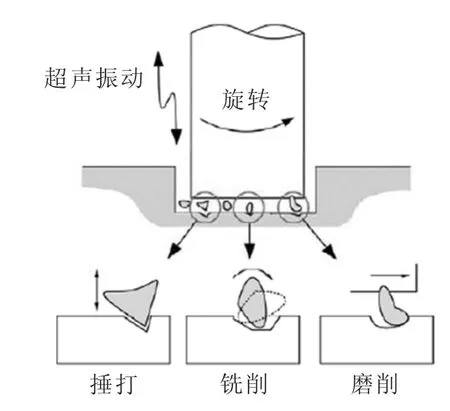
图2 超声加工模型

2 换能器的M-C-K模型

根据超声波换能器的结构，其机械部分由前盖板、锥形喇叭杆和刀具组成，故可建立三者的质量-阻尼器-弹簧（M-C-K）模型（图 3）。

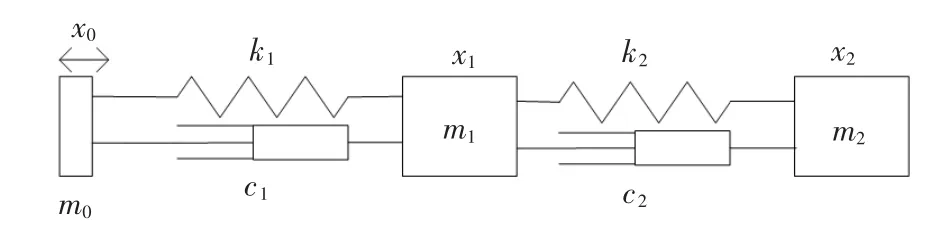
图3 换能器的M-C-K模型

振动M-C-K模型公式可表达为：

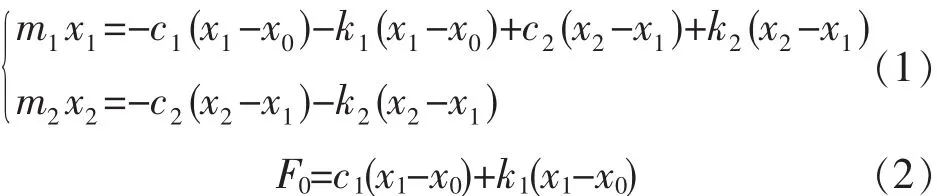
式中：m0为压电陶瓷质量，kg；m1为预紧螺栓与前盖板质量，kg；m2为喇叭杆与刀具质量，kg；c1为预紧螺栓与前盖板阻尼系数；c2为喇叭杆与刀具阻尼系数；k1为预紧螺栓与前盖板弹簧系数，N/m；k2为喇叭杆与刀具弹簧系数，N/m；x0为压电陶瓷位移，m；x1为预紧螺栓与前盖板位移，m；x2为喇叭杆与刀具位移，m；F0为压电陶瓷处喇叭杆受力，N。

换能器的主要结构部件及其材料系数见表1。可知， 图 3 所示模型中，m0=16.2376×10-3kg、m1=23.7542×10-3kg、m2=16.59184×10-3kg。 阻尼系数 c1与c2相等，其值均为0.005。可根据k=AE/L求得刚性系数 k1=288.9637×106N/m、k2=285.2375×106N/m。其中：A为喇叭杆横截面面积；E为弹性模量；L为喇叭杆长度。

利用拉普拉斯等效变换式 （1）所示的M-C-K模型公式，所得结果见式（3）。因此，获得的传递函数见式（4）。通过表1所示的材料和参数，可进一步确定超声波换能器的传递函数，见式（5）。

表1 换能器的结构部件及其材料系数

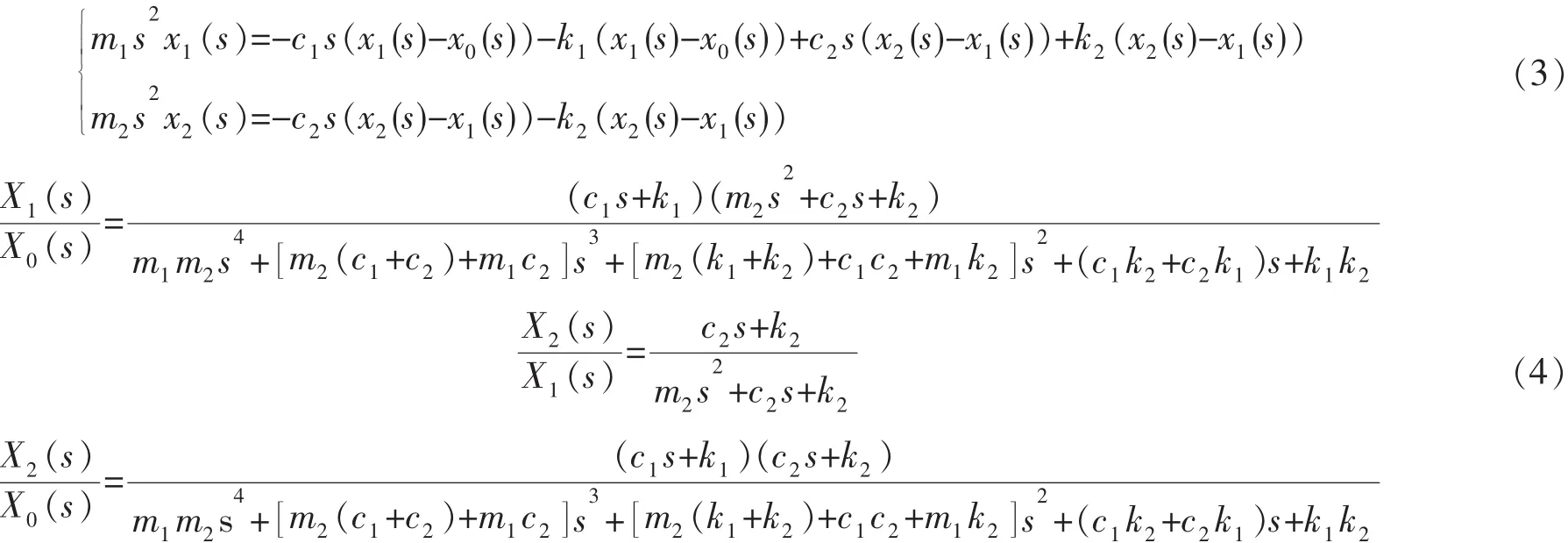
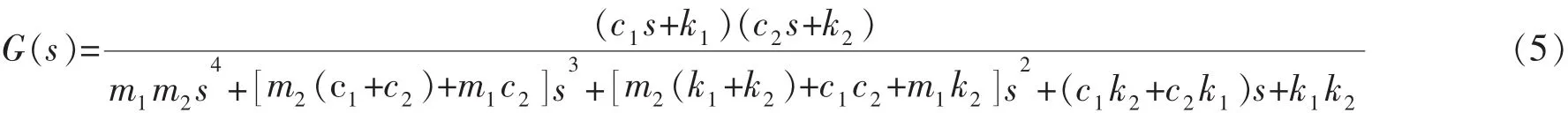
3 有负载情况下换能器的M-C-K模型

3.1 非线性负载情况

在材料加工过程中，超声波换能器的负载被视为切削力，其在加工过程中具有较强的非线性和不稳定性。因此需要模拟其在模型中的加工过程影响，通过计算在负载下的控制系统性能变化，来分析其在加工过程中的影响。

对于非线性负载来说，刀具和工件之间的接触力可用Kelvin-Voigt模型（图4）。其中，负载响应模型示意图作为一个并行工作的M-C-K模型，其描述了超声波换能器动态加载的力学模型。

图4 换能器M-C-K带负载情况

负载的动态响应可描述为：

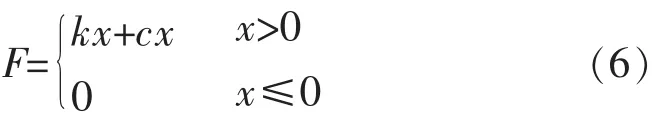
式中：k为接触刚度系数；c为连接弹簧；x为加工刀具的位移。

由于换能器的振动表现为正弦信号，故刀具的位移可被假定为x=ωT，所以切削负荷可确定为：

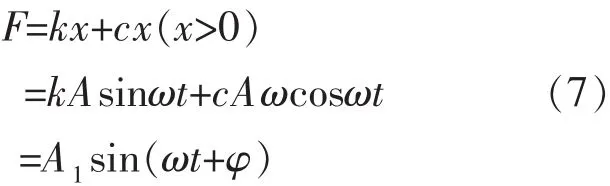
因此，超声加工在有负载情况下的方程可表示为：

通过拉普拉斯变换，可得有负载情况下的方程为：

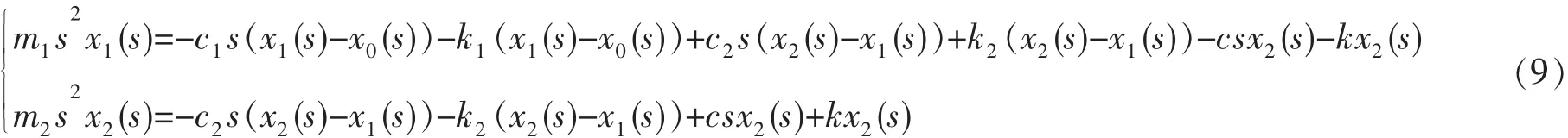
因此，该系统在有负载情况下的传递函数为：

式中：num2=(c1s+k1)·(c2s+k2)；den2=m1m2s4+[m2·(c1+c2)+m1·(c2-c)]·s3+[m2·(k1+k2)+c1·(c2-c)+m1·(k2-k)]·s2+[c1·(k2-k)+(c2-c)·k1]·s+k1·(k2-k)。

3.2 负载切换仿真

在材料去除过程中，超声波换能器的负载进行切换，由于不同的切削力，当负载被打开时，会导致振动不稳定。在Matlab软件的Simulink中建立负荷超声换能器的动力学模型（图 5），其中，G（S）是传递函数，选取采样电阻0.01 Ω对换能器的电流响应性能进行分析。

图5 负载切换仿真

换能器的电流响应仿真结果见图6。其结论是：目前的响应为不稳定的负载时，需要切换；且负载越大，响应越不稳定。

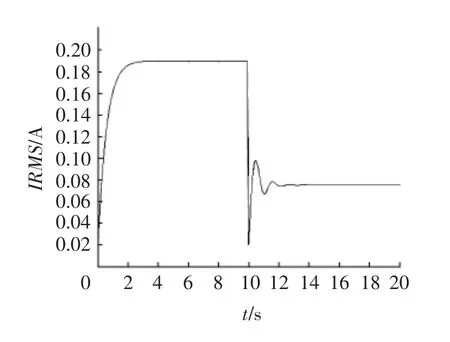
图6 系统无PID控制器的电流响应曲线

图7、图8是用PID控制器和H∞控制器时负载换能器的电流响应曲线。可发现，PID控制器和H∞控制器均可使换能器的电流响应保持不变甚至为负荷开关，且有较小的超调量和比H∞控制器更快的稳态。对于该系统的控制器，其超调量为12.24%，稳态误差为0，调节时间为1.5 s；而H∞控制器系统的稳态误差为0，调节时间为0.74 s。具体计算过程如下：

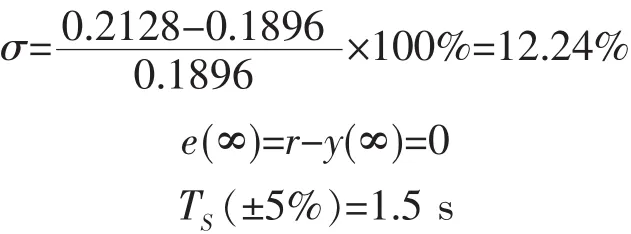
图7 系统有PID控制器的电流响应曲线

图8 H∞控制器的电流响应曲线

4 实验

基于上述分析，设计并制作了超声辅助加工的换能器结构。为了验证换能器的M-C-K模型，对超声波换能器的实验进行了详细研究，包括：阻抗测量、驱动和响应信号及对振动振幅的影响。实验中，非接触式激光测振仪用于测量超声波换能器的振动，阻抗分析仪用于测量换能器的阻抗。

4.1 换能器不同负载的响应

用阻抗分析仪测量换能器在不同负载下的频率特性，结果见图9。可发现，谐振频率为空载65.175 kHz，而拒绝64.875 kHz负载。表明谐振频率在不同负荷时会发生变化。

4.2 不同负载下的振动控制

在不同的控制模式（如：恒定电压、恒定电流、恒定功率）下，对换能器进行振动测试，在3～7 s间进行负载变化测试，其电流和速度振动的输出、输入信号见图10～图12。从数据中发现，当负载变化时，换能器可通过驱动模块的调整保持恒定的振幅，表明该控制方法可有效地抑制负载扰动。由表2显示，在恒流控制模式下，系统振幅的变化率仅为3.9%，而在恒定电压、恒定功率模式下，系统振幅的变化率分别为32%和27%。因此，基于电流反馈的模式是可行的。

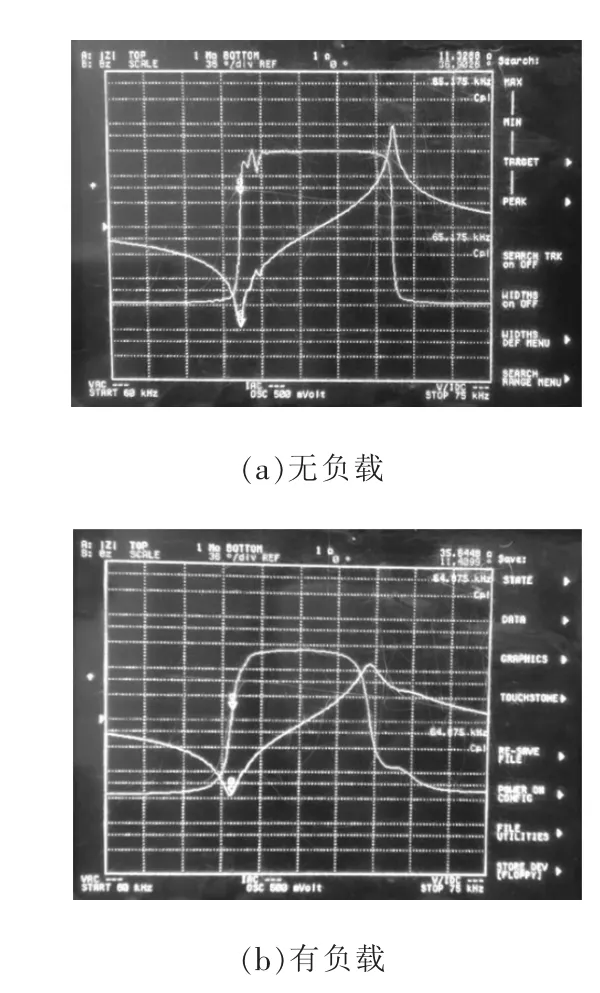
图9 有无负载时的频率阻抗响应曲线

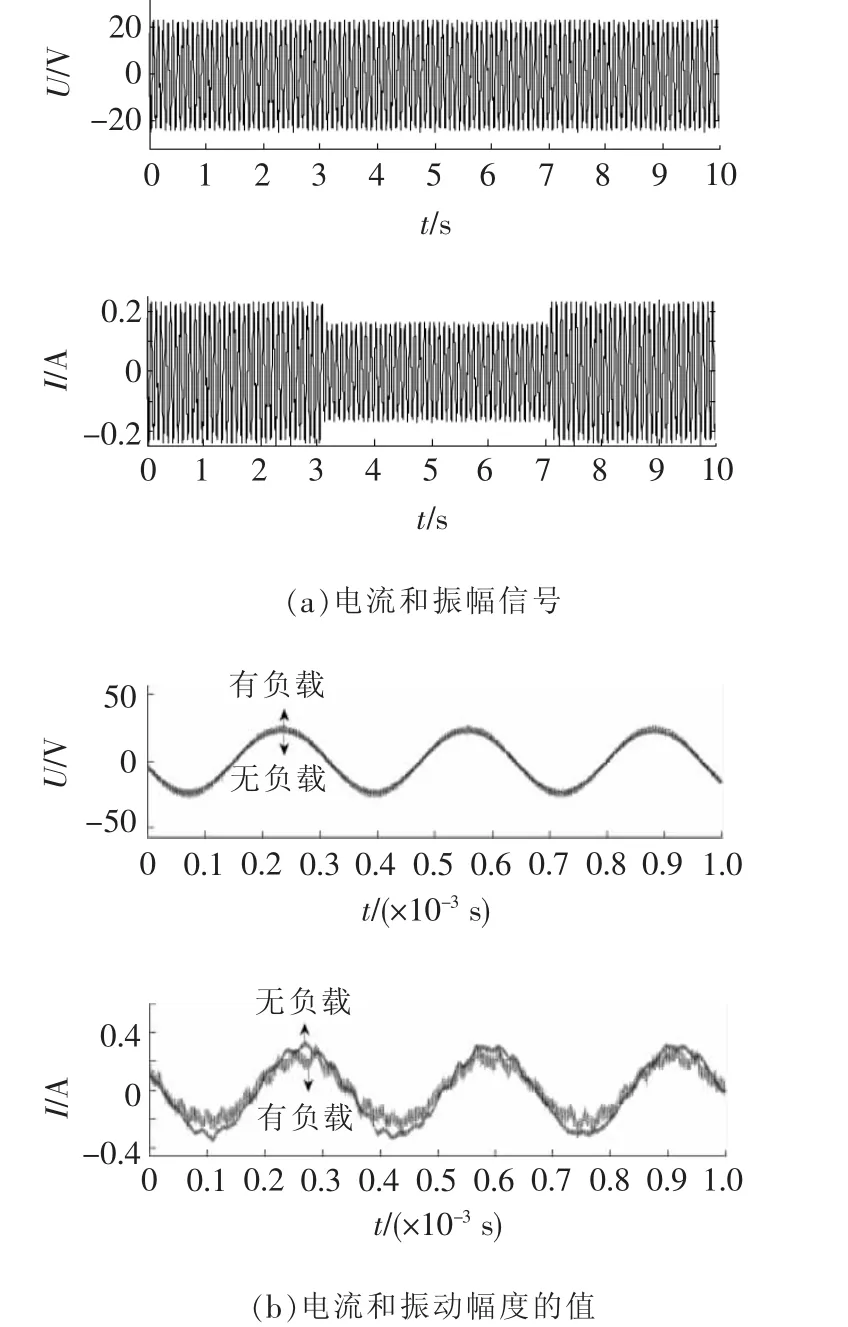
图10 恒电压时，有、无负载情况的对比

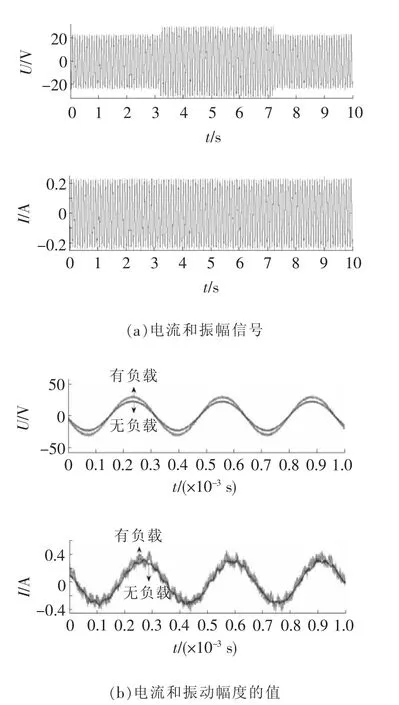
图11 恒电流时，有、无负载情况的对比

图12 恒功率时，有、无负载情况的对比

5 结束语

稳定的振动控制是超声加工的基本要求。本文详细阐述了基于超声波换能器参数的机电模型的系数计算及过程，通过实验验证了所建立的超声振动系统模型的有效性。利用对施加负载的超声波换能器的模型进行仿真，结果表明，超声振动系统模型控制的有效性得到了证实。在恒电压、恒电流和恒功率的条件下，控制器的设计满足负载下的控制系统振幅的要求。

[1] BABITSKY V I，KALASHNIKOV A N，MEADOWS A，et al.Ultrasonically assisted turning of aviation materials[J].Journal of Materials Processing Technology，2003，132（1-3）：157-167.

[2] TSUJINO J，HONGOH M，YOSHIKUMI M，et al.Welding characteristics of 27,40 and 67 kHz ultrasonic plastice welding system using fundamental and high-resonance frequencies[J].Ultrasonics，2004，42（1-9）：131-137.

[3] WANG Fujun，ZHAO Xingyu，ZHANG Dawei，etal.Development of novel ultrasonic transducers for microelectronicspackaging [J].JournalofMaterials Processing Technology，2009，209（3）：1291-1301.

[4] RAJURKAR K P，WANG Z Y，KUPPATTAN A.Micro removal of ceramic material (Al2O3)in the precision ultrasonic machining[J].Precision Engineering，1999（2）：73-78.

[5] MORITA T，KUROSAWA M K，HIGUCHI T，et al.A cylindrical shaped micro-ultrasonic motor utilizing PZT thin film (1.4 mm in diameter and 5.0 mm long stator transducer)[J].Sensors and Actuators A Physical，2000，83（1-3）：225-230.

[6] DUBUS B，HAW G，GRANGER C，et al.Characterization of multilayered piezoelectric ceramics for high power transducers[J].Ultrasonics，2002，40（1-8）：903-906.

[7] CHENG H L，CHENG C A，FANG C C，et al.Singleswitch high power factor inverter driving piezoelectric ceramictransducerforultrasonic cleaner [J].IEEE Transactions on IndustrialElectronics，2010，58 （7）：2892-2905.

简讯

我国特种加工专家、原全国特种加工学会电解加工专业委员会主任、合肥工业大学教授朱树敏先生，因病不幸于2017年8月10日在苏州去世，享年82岁。

Numerical Modeling and Vibration Control of Transducer in Ultrasonic Assisted Machining

ZHANG Jianguo1，LONG Zhili1，LI Zuohua2， ZOU Jianjun2，YANG Yuhui2
（ 1.School of Mechanical Engineering and Automation，Harbin Institute of Technology(Shenzhen)，Shenzhen 518055，China；2.School of Mechanical Engineering，Dongguan University of Technology，Dongguan 523808，China ）

In this paper，a numerical vibration model is established by a mass-damper-elastic component.The loaded effect on the dynamics of the ultrasonic transducer is investigated.The transfer function of transducer is attained and the calculation simulation model is carried out in Matlab.The PID and H∞ algorithm for vibration control is established and simulated in the Matlab Simulink，and found that the PID and H∞ algorithm can achieve the accurate and fast control result.Finally，some experiments to verify the theory and simulation calculation is carried out.

ultrasonic transducer；loaded；vibration controller；ultrasonic assisted machining

TG663

A

1009－279X（2017）04－0043-05

2017-02-17

深圳市基础研究项目（JCYJ20150403161923526）；深圳市南山区创新工业发展专项（KC2015ZDYF0009A）

张建国，男，1989年生，博士研究生。