GMSK调制与非相干解调算法研究与仿真实现

杨泽坤， 晋东立，王 杨

(1.北京跟踪与通信技术研究所，北京 100094；2.中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

GMSK调制与非相干解调算法研究与仿真实现

杨泽坤1， 晋东立1，王 杨2

(1.北京跟踪与通信技术研究所，北京 100094；2.中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

高斯最小频移键控(Gaussian Filtered Minimum Shift Keying,GMSK)是一种连续相位非线性调制方式，具有包络恒定、相位平滑、频谱特性好和带外辐射功率小等多种优点，在移动通信和航天测控等领域得到广泛应用。介绍了GMSK的基本原理，并从频谱效率和包络特性两方面与其他调制方式进行对比分析。同时介绍了几种典型的非相干解调方式，并利用Matlab软件对不同解调方法的性能进行仿真。

高斯最小频移键控；差分相位解调；Viterbi算法；最大似然块检测

0 引言

随着科技的进步与发展，现代通信对调制解调技术的要求越来越高，特别是信号的频谱效率和功率效率等特性要能适应各种条件下的传输需要。针对信号频谱特性的改善，最小频移键控(Minimum Shift Keying,MSK)[1]被提出。它是一种码元相互正交的全响应调制方法，但是其频谱的旁瓣衰落速度已经无法满足现今移动通信对信号带外辐射功率的限制要求[2]。而GMSK就是在MSK的基础上改进的结果[3]。MSK调制的相位累计特性仅仅局限于单一码元内，导致相邻符号之间的相位变化存在跳变。GMSK通过将相位累计扩展到几个连续的相邻码元周期，来扩大相位路径的选择范围。针对GMSK信号的解调技术也可分为相干解调与非相干解调，相干解调需要进行载波恢复，而非相干解调不需要进行载波恢复[4]，结构更加简单，因此非相干解调也得到了广泛的应用。本文将介绍GMSK的调制原理和几种典型的非相干解调方法，调制信号部分将分析GMSK信号与2FSK、DPSK在频谱效率和包络特性上的差异，解调方法部分将对比几种典型的非相干解调方法的性能差异，从而为不同通信场景中选择合适的调制信号与解调方案提供了依据。

1 GMSK调制原理

为了使信号频谱更加紧凑，旁瓣衰落更快，通过在MSK调制前加入预调制滤波器，对基带矩形波进行滤波，使其本身和较高阶的导数都是连续的，得到一种新型的基带波形，从而得到具有较好频谱特性的GMSK调制信号[5]。GMSK的调制原理图如图1所示。

图1 GMSK调制原理

预调制滤波器应具有脉冲响应过冲小、带宽窄和截止特性陡峭等特点，以防止出现过大的瞬时频偏，并抑制高频分量，降低带外辐射功率等。高斯低通滤波器[6]是一种满足上述特性的预调制滤波器，其单位冲激响应为：

(1)

式中，α与预调制高斯滤波器的3 dB带宽Bb之间的关系为：

(2)

假设在滤波器前输入双极性不归零矩形脉冲序列s(t)：

(3)

式中，Tb为码元间隔。高斯预调制滤波器的输出为：

(4)

式中，g(t)为高斯预调制滤波器的脉冲响应：

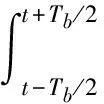
(5)

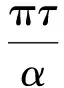
(6)

式中，

(7)

BbTb是时间-带宽积，BbTb值越小，高斯信号时域上的时延就越长，在频域所占的带宽就越小[7]。BbTb在0.1～0.5间的GMSK脉冲形状如图2所示。

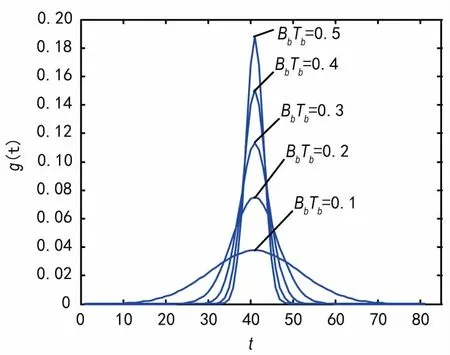
图2 高斯滤波器矩形脉冲响应波形

为了进一步探究GMSK信号的特性，可以从频谱效率和包络特性2个方面来分析。为此，选择将GMSK与二进制DPSK、FSK的调制方式进行对比。对于GMSK调制，采用BbTb=0.5，对于2FSK调制，频率间隔设置为0.5倍的符号速率。

在信息传输速率相同的条件下，仿真分析3种调制方式等效基带信号的功率谱密度，结果如图3所示。由图中结果可以看出，2FSK的功率谱最宽，其频谱效率最低。GMSK信号相比DPSK信号功率谱的主瓣宽度窄，而且GMSK信号功率谱的旁瓣功率远低于DPSK，因此具有更高的频谱效率。

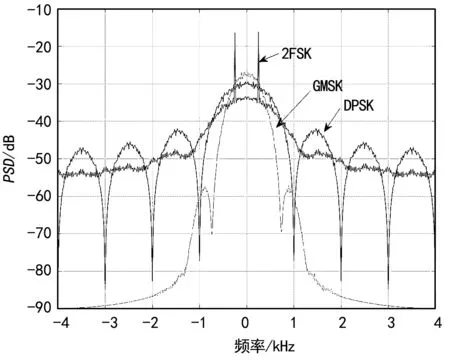
图3 3种调制方式的功率谱密度

进一步对比3种调制方式的频谱效率，对二进制DPSK信号，采用滚降因子为0.3的根升余弦滤波器进行成形滤波。DPSK信号成形滤波后的功率谱密度曲线如图4所示。对比3种调制方式可知，GMSK信号功率谱的主瓣宽度与成形后的DPSK信号相近，但GMSK信号仍然具有较低的旁瓣，且旁瓣下降较快。这一特点将使GMSK发射信号具有更稳定的包络。

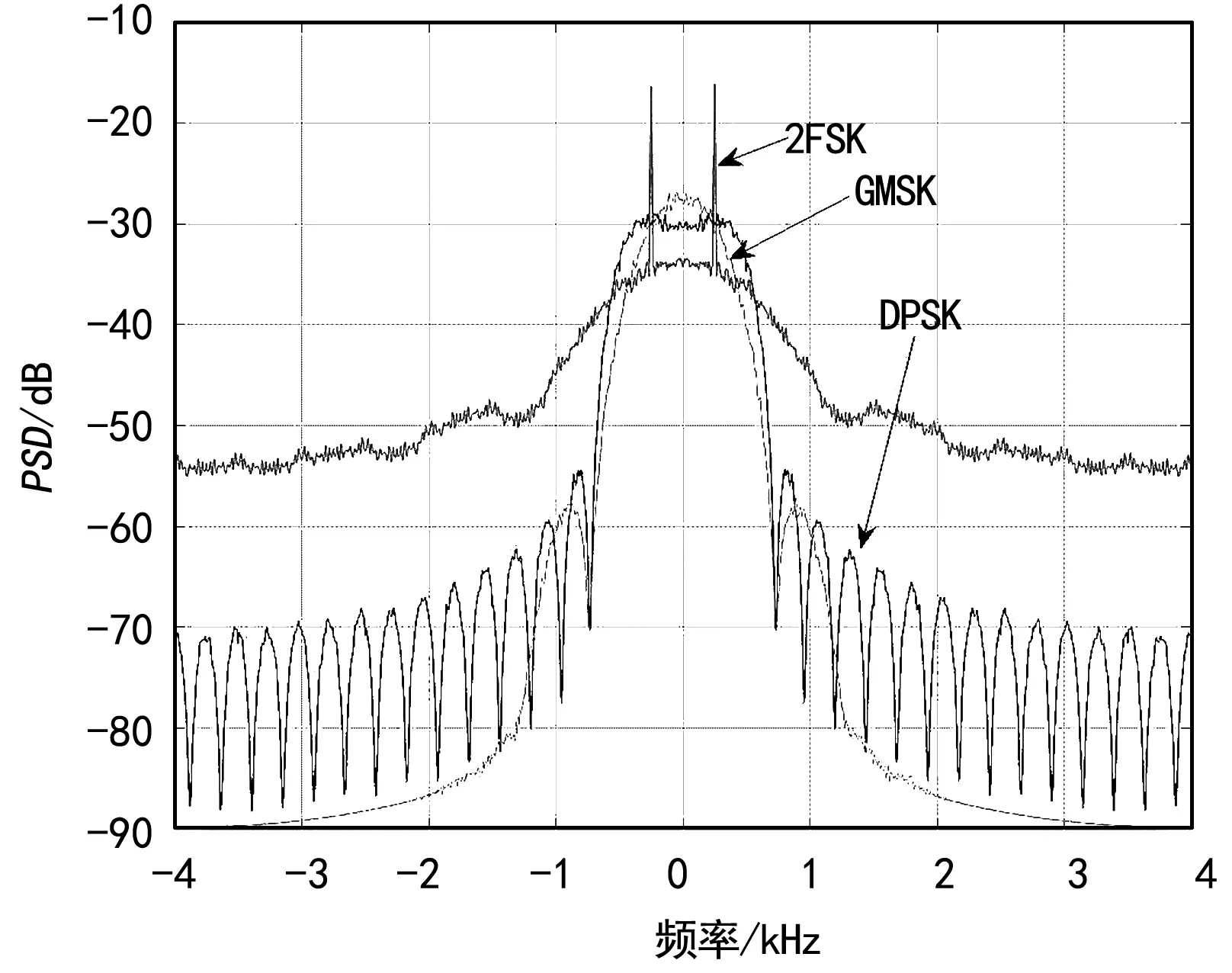
图4 3种调制方式的功率谱密度

DPSK发射信号和GMSK发射信号的时域波形如图5和图6所示。对比图中结果可知，DPSK信号经过成形滤波后，旁瓣能量受到抑制，导致时域信号幅度出现起伏，即包络不断起伏变化。GMSK信号由于旁瓣能量较小，因此发射信号的包络较稳定。

图5 DPSK调制信号

图6 GMSK调制信号

综合对比来看，3种调制方式中FSK信号会占用较大带宽，频偏利用率较低；DPSK信号与GMSK信号相比具有相近的主瓣宽度，但旁瓣能量稍大，发射信号包络起伏；GMSK信号旁瓣下降较快、能量较低，同时具有恒包络的特性。

2 基于GMSK调制的非相干解调原理

本节将对差分相位解调中的1-bit差分相位解调、2-bit差分相位解调以及基于Viterbi译码算法的差分相位解调、最大似然块检测的原理进行介绍，并对比几种非相干解调算法的性能。

2.1 1-bit差分相位解调

GMSK调制方案中相邻码元之间的相位变化为±π/2。如果接收信号经过T延时后，再对信号附加π/2的相位变化，则此时相邻码元之间的相位变化变为0或π，可以直接通过符号判决进行解调[8]。1-bit差分相位解调原理如图7所示。

图7 1-bit差分相位解调原理

假设接收到的信号表示为：

s(t)=A(t)cos(ωct+θ(t))，

(8)

式中，A(t)是由信道衰落引起的时变包络(理想情况下可看为为常数)。接收到的信号经过1 bit延时和π/2的相移得到F(t):

F(t)=A(t-T)cos(ωc(t-T)+θ(t-T)+π/2)。

(9)

然后F(t)和s(t)相乘后得到x(t)：

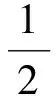
{sin(θ(t)-θ(t-T)+ωcT)-

sin(2ωct-ωcT+θ(t)+θ(t-T))}。

(10)

经低通滤波器滤波后，若ωcT=2kπ(k∈Z)，则1 bit差分解调的输出为：

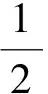
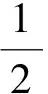
(11)

在(k+1)T时刻对y(t)进行采样得到y((k+1)T)，它的符号判决取决于Δθ((k+1)T)，因此就可以得到如下判决规则：

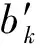
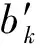
2.1 2-bit差分相位解调

2-bit差分相位解调[11]的原理如图8所示。

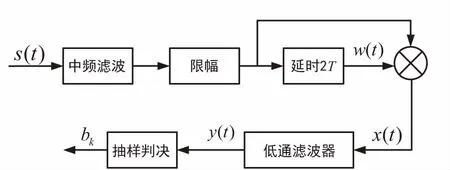
图8 2-bit差分相位解调原理

接收到的GMSK信号经过一个中频滤波器滤波，经过限幅器将振幅的影响去掉，然后再与延迟2个码元周期的信号相乘，得到输出的信号：

x(t)=w(t)s(t)=A(t)A(t-2T)cos(ωct+θ(t))·

cos(ωc(t-2T)+θ(t-2T))。

(12)

通过低通滤波器后输出：

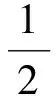
(13)

式中，

Δθ(2T)=θ(t)-θ(t-2T)=θ(t)-θ(t-T)+

θ(t-T)-θ(t-2T)。

(14)

若2ωcT=2kπ(k∈Z)时，

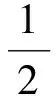
{cos(θ(t)-θ(t-T))cos(θ(t-T)-θ(t-2T))-

sin(θ(t)-θ(t-T))sin(θ(t-T)-θ(t-2T))}=

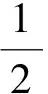
(15)

式中，

M(t)= cos(θ(t)-θ(t-T))×

cos(θ(t-T)-θ(t-2T)),

(16)

N(t)= sin(θ(t)-θ(t-T))×

sin(θ(t-T)-θ(t-2T)),

(17)

在发送端对发送数据ak进行差分编码，即可以使得N(t)的两项乘积等效于ck⊗ck-1。GMSK的差分编码调制原理框图如图9所示。

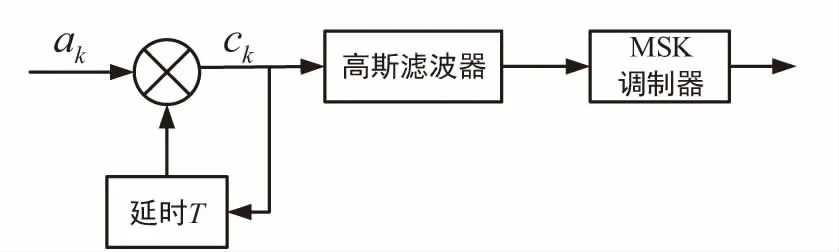
图9 GMSK差分编码调制原理

当限幅器输出为1，2ωcT=2kπ(k∈Z)时，假定直流分量M(t)=γ≥0，而N(t)的值在kT时刻可正可负。若前一个码元与当前码元相同，N(t)>0；如果前一个码元与当前码元不同，则N(t)<0。若y(kT)>γ，则表示解调器在第k个码元和第k-1个码元输入信息所对应的差分编码码元不一样，那么判定信息码(初始绝对码)为1，否则判定为0。

经过以上分析得到了GMSK 2-bit差分解调的判决规则：

若y(kT)>γ，判决为1；

若y(kT)<γ，判决为0。

由以上分析可以看出，1-bit差分解调和2-bit差分解调共同的特点是均不需要相干载波的恢复，解调结构比较简单；不同在于1-bit差分解调是对每个码元进行处理，不需要对初始数据进行差分编码，而2-bit差分解调需要对初始输入码元差分编码，并且最后的判决门限附加了一个直流分量，并不是零。

2.2 基于Viterbi译码算法的差分相位解调

维特比在1967年提出了基于最大似然序列检测的Viterbi译码算法[12]。Viterbi译码是使整个信息比特序列译码的差错概率最小的最佳译码算法。Viterbi算法的基本思路是对接收信息序列和状态网格图上所有的可能序列进行比较，寻找与接收序列距离最小的路径作为译码输出。

由于GMSK固有的码间串扰，使得直接判决的解调器的误码率性能较差。为了提高其误码率性能，在差分解调的基础上，可利用Viterbi算法对GMSK进行解调[13]。基于Viterbi算法的差分相位解调原理框图如图10所示。

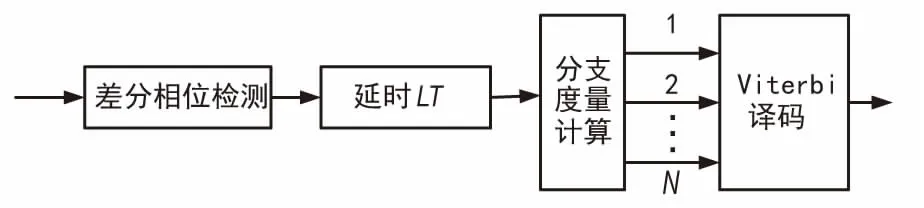
图10 基于Viterbi算法的差分相位解调原理

以1-bit差分相位解调为例，相位差分信号在第k个符号周期的采样点可以表示如下：

Δθ(kT)=θ(kT)-θ(kT-T)=

(18)

假设高斯脉冲长2L+1个符号周期，可以定义

(19)

差分相位表达式可以简化为:

(20)

对于给定BT参数的GMSK信号，由于其成形脉冲g(t)已知，因此φk-i可以确定。定义状态Sk=(ak-L,…,ak-1,ak+1,…,ak+L)，则差分相位Δθ(kT)可以由状态Sk和输入ak决定。状态转移过程与卷积编码类似，因此可以利用Viterbi算法进行最大似然判决。

Viterbi算法中，从状态Sk转移到Sk+1时，所有对应的分支度量可以定义为：

BM(Sk,Sk+1)=((Δθk-L-P(Sk,Sk+1))mod2π)2,

(21)

式中，P(Sk,Sk+1)表示理想条件下从状态Sk转移到Sk+1时的差分相位标准值，可以根据所有可能的输入序列通过下式计算得到:

(22)

根据得到的分支度量和幸存路径度量，可以得到第k+1个码元的总相位路径度量：

M(Sk+1)=M(Sk)+BM(Sk,Sk+1)。

(23)

按照总路径度量最小的原则，淘汰度量较大的路径，得到GMSK 信号的最优相位路径，进而可以判决恢复出发送的信息序列。

2-bit差分的Viterbi译码算法原理上与1-bit差分相位Viterbi译码算法基本一致，只是差分运算时时延变为2个符号周期。相位差分信号在第k个符号周期的采样点可以表示为：

Δθ(kT)=θ(kT)-θ(kT-2T)=

(24)

可见，差分相位Δθ(kT)可以由(ak-L-1,…,ak-1,ak+1,…,ak+L)和输入ak决定，一个符号周期内状态数变为22L+1个，每个码元间隔结束时需要计算的分支度量为22L+2个，比1-bit差分Viterbi译码增加了一倍，同时解调性能得到改善。

2.3 最大似然块检测

假设GMSK调制信号成形脉冲约束长度为L个符号周期，则信号的相位在时间t可以表示为:

θ(t,a)=φ(t,Cn)-θn，

(25)

式中，φ(t,Cn)和θn分别为：

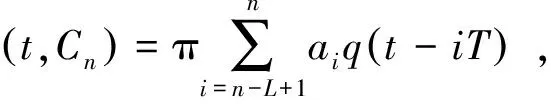
(26)

(27)

将GMSK信号相位表达式代入接收信号r(t)关于参考信号s(t,a)和初始相位θ的条件概率中，可得：

P(r(t)|s(t,a),θ)=

(28)

式中，A为参考信号幅度；N0为高斯白噪声功率谱密度。β定义为：

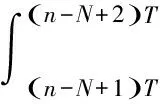
(29)

式中，Cn=(an-L+1,…,an)。对似然函数关于初始相位取平均，消除未知变量的影响，可得

(30)

式中，F′ 为与参考信号无关的常量；I0(x) 为零阶修正贝塞尔函数，是自变量的增函数。因此，选择使似然函数最大的参考信号，就是选择发送符号序列，使得|β|达到最大值。

(31)

参数Dk可以通过下式递归运算得到:

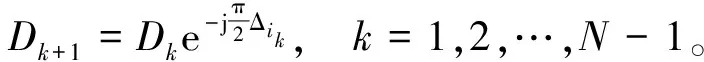
(32)

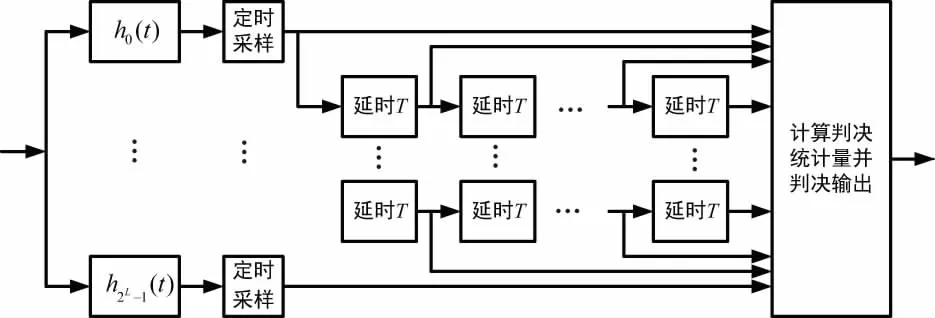
图11 最大似然块检测原理

3 仿真实现及结果分析

建立GMSK调制解调系统模型，仿真分析3类非相干解调方案的性能。发送端采用BT值为0.5或0.7的GMSK调制方式；接收端分别采用1-bit差分相位、2-bit差分相位、基于Viterbi算法的1-bit差分相位、基于Viterbi算法的2-bit差分相位和最大似然块检测5种非相干解调方法，最大似然块检测算法中的观测符号数N设定为4。

BT值为0.5时5种非相干解调方案的误码性能如图12所示。

图12 非相干解调方案误码性能

由图12可知，差分相位解调方案的性能相对较差，1-bit差分相位解调性能最差。基于Viterbi算法的差分相位解调方案通过增加Viterbi译码，能够获得相比差分相位解调更优异的性能。最大似然块检测方案的误码性能与基于Viterbi算法的2-bit差分相位解调相近，并且在低信噪比条件下性能稍好。

BT值为0.7时5种非相干解调方案的误码性能如图13所示。图13中结果显示，5种非相干解调方案的误码性能与BT值为0.5时的规律基本一致。GMSK调制参数BT值变为0.7时，最大似然块检测方案的性能优于基于Viterbi算法的2-bit差分相位解调。

图13 非相干解调误码方案性能

4 结束语

本文介绍了GMSK调制的基本原理以及1-bit差分相位解调、2-bit差分相位解调、基于Viterbi译码算法的差分相位解调、最大似然块检测4种非相干解调方法，并从频谱效率、包络特性、解调性能几个方面进行仿真实现，分析的结果可以为根据通信实际需求在方案选择时提供参考。例如，在高速跳频卫星通信中，受限于卫星信道和跳频通信的特点，调制方式应该具有恒包络特性并支持非相干解调，而GMSK不仅满足这2个条件，在频谱效率方面相比其他的调制方式也更具有优势。

[1] SIMON M.A Generalization of Minimum-Shift-Keying (MSK)-Type Signaling Based Upon Input Data Symbol Pulse Shaping[J].IEEE Transactions on Communications,2003,24(8):845-856.

[2] 朱磊.突发GMSK信号分析与解调技术的研究与实现[D].长沙：国防科学技术大学,2013.

[3] MUROTA K,HIRADE K.GMSK Modulation for Digital Mobile Radio Telephony[J].IEEE Transactions on Communications,1981,29(7):1044-1050.

[4] 漆钢.小BT参数突发GMSK信号解调技术研究[D].绵阳：中国工程物理研究院,2013.

[5] 赵彦惠.基于相位累加实现GMSK调制的技术分析[J].无线电工程,2013,43(3):20-23.

[6] 张骞,邵宝杭.一种基于软件无线电思想的GMSK调制设计[J].电子设计工程,2012,20(19):151-153.

[7] 杨雪丽,郑碧月,朱广良.GMSK调制信号的仿真[J].信息技术,2004,28(3):13-15.

[8] 熊于菽.GMSK调制解调技术研究[D].重庆：重庆大学,2007.

[9] 丁兴文,朱智勇,李海涛.基于维特比算法的GMSK信号非相干解调技术研究[J].遥测遥控,2011,32(1):18-21.

[10] 张梦瑶,张有志.一种π/4-DQPSK和GMSK调制可变信号一体化解调技术[J].无线电工程,2015，45(2):30-33.

[11] 吴团锋.基于2比特差分的GMSK信号解调算法[J].军事通信技术,2002(1):36-41.

[12] FORNEY G D J.The Viterbi Algorithm[J].Proceedings of the IEEE,1993,61(5):268-278.

[13] 曾佐祺,李赞.基于Viterbi算法的GMSK信号解调性能分析与仿真[J].重庆邮电大学学报(自然科学版),2008,20(2):132-138.

ResearchandSimulationImplementationofGMSKModulationandNoncoherentDemodulationAlgorithm

YANG Ze-kun1,JIN Dong-li1,WANG Yang2

(1.BeijingInstituteofTrackingandTelecommunicationsTechnology,Beijing100094,China; 2.The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China)

Gaussian Filtered Minimum Shift Keying (GMSK) is a kind of nonlinear continuous phase modulation,with advantages of constant envelope,smooth phase,good spectrum characteristics,lower out-of-band radiation power,widely used in mobile communications and aerospace telemetry and control.This paper introduces the basic principle of GMSK,compared with other modulation methods in spectrum efficiency and envelope characteristics.In the meantime,several typical noncoherent demodulation methods are introduced,and their performance are simulated by using Matlab software.

GMSK;DPD;Viterbi algorithm;MLBD

10.3969/j.issn.1003-3106.2017.12.14

杨泽坤,晋东立,王杨.GMSK调制与非相干解调算法研究与仿真实现[J].无线电工程,2017,47(12):61-66，82.[YANG Zekun,JIN Dongli,WANG Yang.Research and Simulation Implementation of GMSK Modulation and Noncoherent Demodulation Algorithm[J].Radio Engineering,2017,47(12):61-66，82.]

TN911.22

A

1003-3106(2017)12-0061-06

2017-05-17

中国博士后科学基金资助项目(2016M601286)。

杨泽坤男，(1993—)，硕士研究生。主要研究方向：信道编码、卫星通信。

晋东立男，(1963—)，硕士生导师，研究员。主要研究方向：无线通信。