基于ADMM的惩罚函数构造方法优化
2017-11-07陈紫强王广耀
陈紫强,王广耀
(桂林电子科技大学 信息与通信学院,广西 桂林 541000)
基于ADMM的惩罚函数构造方法优化
陈紫强,王广耀
(桂林电子科技大学 信息与通信学院,广西 桂林 541000)
为了提升传统交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)惩罚译码算法的误码性能和收敛速率,对罚函数做进一步优化,提出一种基于三段式罚函数的ADMM惩罚译码算法(Three-Segment ADMM-Penalized Decoding,TS-ADMM-PD)。通过引入过渡函数,其斜率介于前后两段函数之间,达到折衷译码性能和收敛速度的目的。优化后的罚函数在x=0和x=1附近斜率较大,以增强对伪码字的惩罚力度,降低误码率并加快译码收敛;在x=0.5附近斜率较小,以便此处的变量节点信息进行传递。仿真结果表明,相比于I-ADMM-PD算法,所提的TS-ADMM-PD算法有着更优秀的误码性能和收敛速度。
LDPC码;交替方向乘子法;惩罚函数;误码性能;收敛速度
0 引言
低密度奇偶校验(Low-Density Parity-Check,LDPC)码是Gallager博士于1962年提出的一种线性分组码[1],是迄今为止发现的误码性能最接近香农极限的码字之一,成为继Turbo之后信道编码领域的研究热点。线性规划(Linear Programming,LP)最早由J.Feldman提出作为置信传播(Belief Propagation,BP)译码的备选方案[2],然而在实际应用中,LP译码存在收敛速度慢、难以硬件实现等弊端。针对这一问题,国内外研究人员展开了大量研究[3-6]。
为了解决LP译码算法收敛速度慢的问题,文献[3-7]提出了基于ADMM的LP译码方案。由于ADMM技术具有分布式运算、并行处理的特点[8],从而加快译码收敛速率核心思想是通过引入辅助矢量z与传输码字x交替更新。然而,该算法在低信噪比区域误码率仍然很高。为了进一步改善低信噪比区域的误码性能,文献[9-14]通过引入惩罚项,避免码字解为伪码字,从而降低误码率,但同样造成了高信噪比区域的错误平层问题。文献[15]通过对罚函数进行重构,降低了ADMM惩罚译码的误码率,不过该算法的罚函数结构还可以继续完善,误码率有待进一步降低。
本文针对传统ADMM惩罚译码算法提出一种改进方案TS-ADMM-PD。充分利用惩罚函数的结构特点,对罚函数做进一步优化,引用过渡函数对译码性能和收敛速度进行折衷。优化后的罚函数更加细分了在不同端点处斜率的取值,最终所提的TS-ADMM-PD算法在仅增加少量计算复杂度的条件下,译码性能和收敛速度均有所改善。
1 LP译码
考虑长度为N的二进制LDPC码C,校验矩阵为HM*N,其中M为校验节点数,N为变量节点数(M≤N)。令I=(1,2,...,N)和J=(1,2,...,M)分别代表变量节点集合和校验节点集合。所有的变量节点度数为dv,校验节点度数为dc,可用Tanner图来表示。Hij=1表示变量节点vi与校验节点ci之间有一条相连的边。Nc(j)和Nc(j)i分别表示变量节点中与校验节点ci相邻的节点及除变量节点i外校验节点j的所有相邻节点,Nv(i)和Nv(i)j分别表示校验节点中与变量节点vi相邻的节点及除校验节点j外变量节点i的所有相邻节点。
对于一给定码C,定义其码字多面体为码C中所有有效码字的凸包,记为Conv(C)。如果LDPC码在有噪声的信道中传播,则LP译码问题可被转化为码字多面体上的线性规划问题。码字多面体的顶点与传输码字相对应,码字多面体上的每一点都是传输码字的凸组合,并且线性规划译码的最优解总是在码字多面体的顶点处取得[16]。设传输码字为x∈C,接收矢量为y,则LP译码问题可被表达为一般形式如下:
式中,γ表示对数似然比(LLR)矢量;Tj表示选出与校验节点j对应的码字x的分量;PPdj表示所有由长度为dj且包含偶数个元素‘1’的二进制矢量构成的凸包,称为检验多面体。
综上所述,线性规划译码是一种基于最优化技术的译码方案,主要思想是将译码问题转化为数学上的整数规划问题[17]。通过松弛约束条件,将原先难以解决的LP问题分解为小的、易于处理的简单LP问题,然后再利用最优化理论完成整个译码过程[18]。不过仍然存在瀑布区临界值较大、硬件实现复杂度高等问题[19]。
2 ADMM惩罚译码
为了改善LP译码在低信噪比时的误码性能,加快译码收敛,提出了基于ADMM的改进惩罚译码算法(I-ADMM-PD)。该方法的主要思想为向LP译码的目标函数中添加一个惩罚项,将译码问题转化为数学上非线性非凸优化问题,此时的目标函数被改变为:
基于ADMM的惩罚译码问题可写为一般形式:
式中,β为惩罚系数;g(xi)为引入的惩罚函数,对译码错误的码字进行惩罚。随着迭代次数的增加,渐趋于正确译码。 ADMM惩罚译码算法过程如下:
① 对于∀j∈J,构建转换矩阵Tj和接收矢量r的对数似然比γ;
② 设置最大解码迭代次数Tmax为50,译码容差值ε为3.8×10-5;
③ 对于∀j∈J,将拉格朗日乘子矢量yj中的所有元素初始化为0,将辅助矢量zj中的所有元素初始化为0.5。迭代次数k初始化为0;

由γi计算初始解矢量x0,γi为线性规划目标函数的系数。对于∀i∈I,有
式中,xi=∏[0,1](xi)为xi在[0,1]间隔上的投影,总是选取离x=0.5最远的驻点;

yj+1=yj+μ(Tjx-zj);
文献[20]中定义了2个不同的惩罚函数g1(x)和g2(x),g1(x)=-α|x-0.5|,g2(x)=-α(x-0.5)2。这里α>0为常量,取值依赖于具体的译码问题,应选取能加快收敛速度的α值。
ADMM惩罚译码器进行迭代译码的过程中,z和y的更新规律保持不变;在基于ADMM的x更新中:
通过对xi的表达式进行求导,然后令其为零,得到驻点从而求得局部解。由函数性质得到,惩罚函数g(x)在g1(x)(0,0.5)上单调递增。所以如果存在多个驻点,采用简单的阈值总是选择离0.5最远的那个。
①l1惩罚译码:采用ADMM算法,利用g1(x)=-α|x-0.5|,将译码问题转换为解决以下的线性规划问题:
目标函数为f(x)=γTx-α‖x-0.5‖1,则其(xf)i=γi-αsgn(xi-0.5),其中xf表示f(x)关于x的微分。令给定一个ti值,xi有2个解,总是选择离0.5更远的那个解,取阈值ti=di/2,di为第i个变量节点的度数,x的分量xi的更新规律归纳如下:
②l2惩罚译码:采用ADMM算法,利用g2(x)=-α|x-0.5|,将译码问题转换为解决以下的线性规划问题:
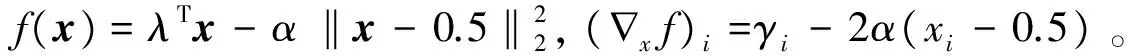
3 TS-ADMM-PD算法
正如本文之前所提,要改善译码性能,加快译码收敛速度,需加大惩罚函数在x=0及x=1附近的斜率以增加对伪码字的惩罚力度;减小在x=0.5附近的斜率以便ADMM译码器对变量节点信息进行转换。文献[20]中给出了3种不同形式的惩罚函数,g1(x),g2(x)上文中已给出,现给出罚函数g3(x)=-lg(|x-0.5|),且证明了惩罚函数为对数函数时的译码性能不及前2种。从3个函数曲线中可以看出,在(0,0.5)区间上,g1(x)的斜率恒定为1,g2(x)的斜率从1递减到0,g3(x)的斜率从2lge递增到+;在(0.5,1)区间上的斜率则恰恰相反。将g3(x)的斜率变化与g1(x),g2(x)相对比可得到结论,惩罚函数在(0,1)区间两端附近的点处斜率应该避免取较小的值,在x=0.5附近的点斜率应取较小的值。
所设计的罚函数结构,需满足在(0,1)区间上对称,且斜率在区间两端较大,在x=0.5处较小,容易联想到构造分段函数以尽可能满足要求。对于g1(x)和g2(x),文献[20]将(0,0.5)之间的罚函数划分为2个函数段,一定程度上降低了误码率并加快译码收敛。本文的设计思想是对二段分段罚函数进行再一步的划分以得到更优秀的误码性能。
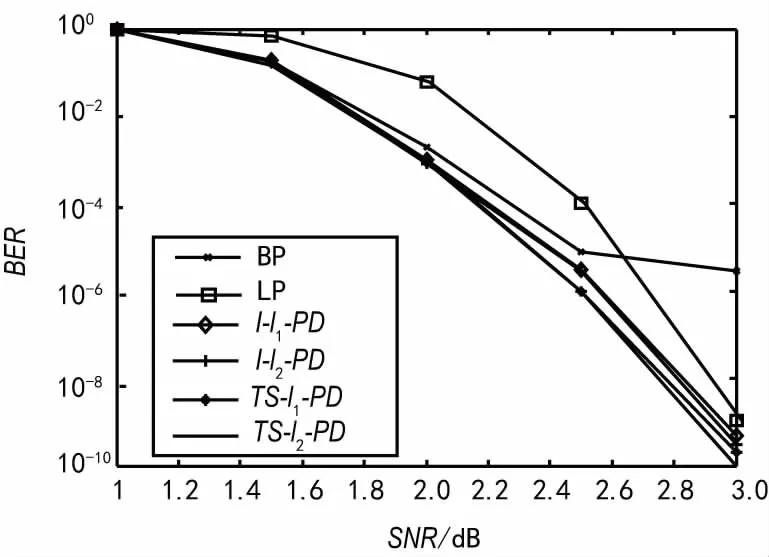
对于罚函数g1(x),选取数a,b(0 将构造的罚函数命名为TS-l1-PF,表示为: 结合上文中给出的xi和ti的表达式及所构造的罚函数g(x),得到以TS-l1-PF为罚函数ADMM惩罚译码的码字x的更新规律如下: 式中,ρ为罚函数TS-l1-PF的第一、二、五、六段的惩罚系数;β为第三、四段的惩罚系数。 对于罚函数g2(x),选取数c,d(0 将构造的罚函数命名为TS-l2-PF,表示为: 式中,k0>1,k=2(0.5-d),0 结合给出的xi和ti的表达式及所构造的罚函数g(x),得到以TS-l2-PF为罚函数ADMM惩罚译码的码字x的更新规律如下: 式中,λ为罚函数TS-l2-PF第一、二、四、五段的惩罚系数;β为TS-l2-PF第三段的惩罚系数。所设计的罚函数如图1所示。 图1 TS-l1-PF和TS-l2-PF罚函数图像 可知,ADMM惩罚译码性能对罚函数的选取比较敏感,本文为了满足预期的译码需求,引入大量参数来构造罚函数。然而,如何取得这些参数的最优解是个很棘手的问题。本文按照各参数的取值范围构造一个有限集合,然后依次进行仿真比较。令 为了验证基于本文所构造罚函数的译码算法的有效性,选取2种规则LDPC码C1和C2,C1为[2640,1320]“Margulis”码,行重为6,列重为3,码率为0.5;C2为[999,888]高码率“MacKay”码,码率为0.89。设置ADMM惩罚因子μ=5,过松弛系数ρ=1.9,译码容差值ε为3.8×10-5。通过仿真,对不同译码方法的性能和收敛速度进行分析比较。码C1在不同性噪比情况下,BP、LP、I-ADMM-PD、TS-ADMM-PD算法的译码性能比较如图2所示。由图2可看出,与BP算法相比,当信噪比大于2.6 dB时,LP译码可以改善译码性能且没有错误平层,而此时BP译码出现了错误平台现象。相较于LP译码,I-ADMM-PD算法改善了低信噪比(SNR<2.4 dB)区域的译码性能且接近BP算法,同时在高信噪比(SNR>2.4 dB)区域也没有发生错误平层现象,因此性能优于BP、LP译码。TS-ADMM-PD算法则在其基础上进一步降低了误码率。2种改进惩罚译码算法中,我们发现TS-l2-PD具备更优秀的纠错性能。 码C2在不同性噪比条件下,LP、TS-ADMM-PD算法的译码性能如图3所示。从图3中可以看出,相较于LP译码,I-ADMM-PD算法改善了低信噪比(SNR<5 dB)区域的译码性能;然而在高信噪比(SNR>5 dB)区域,LP译码的误码率开始逐渐低于TS-ADMM-PD,此时可将惩罚项置0,便可实现LP译码。因此,对于高码率的码字,TS-ADMM-PD算法仍具备优异的译码性能。 图2 码C1条件下的的误码性能比较 图3 码C2条件下的的误码性能比较 图4 码C1条件下的迭代次数变化曲线 码C1取不同α值时,I-ADMM-PD与TS-ADMM-PD算法译码的迭代次数如图4所示,设置最大迭代次数Tmax为1 000。在2种信噪比情况下,0.5<α<3.5时,改进后的TS-ADMM-PD算法的译码迭代次数要小于I-ADMM-PD。尤其是当α=2,信噪比为3 dB时,TS-ADMM-PD算法的迭代次数为50左右,比I-ADMM-PD算法减少了10次,译码收敛速度提升了近1.2倍。 针对传统ADMM惩罚译码算法误码性能不理想,收敛速度慢的问题,提出了基于三段式罚函数的TS-ADMM-PD算法。在(0,a)区间两端和(b,0.5)之间分出一段过渡函数,将误码率和收敛速率进行折衷。仿真实验表明,对于中高码率的码字,与I-ADMM-PD算法相比,本文所提算法在一定信噪比区域降低了误码率,在特定的α范围内译码收敛速度提升近1.2倍,具有一定的工程应用价值。 [1] GALLAGER R.Low-density Parity-check Codes[J].IRE Transaction on Information Theory,1962,8(1):21-28. [2] FELDMAN J.Decoding Error-correcting Codes via Linear Programming[M].Massachusetts Institute of Technology,2003. [3] DEBBABI I,GAL B L,KHOUJA N,et al.Analysis of ADMM-LP Algorithm for LDPC Decoding,a First Step to Hardware Implementation[C]∥IEEE International Conference on Electronics,Circuits,and Systems.IEEE,2015:356-359. [4] ZHANG X,SIEGEL P H.Efficient Iterative LP Decoding of LDPC Codes with Alternating Direction Method of Multipliers[C]∥IEEE International Symposium on Information Theory Proceedings.IEEE,2013:1501-1505. [5] WEI H,JIAO X,MU J.Reduced-complexity Linear Programming Decoding Based on ADMM for LDPC Codes[J].IEEE Communications Letters,2015,19(6):909-912. [6] 范庆辉,慕建君,焦晓鹏,等.基于加速交替方向乘子法的LDPC码线性规划译码方法[P].陕西:CN104092468A,2014-10-08. [7] 王勇超,白晶,杜倩.基于最小多面体模型的LDPC码线性规划译码方法[P].陕西:CN105959015A,2016-09-21. [8] BOYD S,PARIKH N,CHU E,et al.Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers[M].Found.Trends Mach.Learn,2011:1-122. [9] LIU X,DRAPER S C.ADMM LP Decoding of Non-binary LDPC Codes in MathbbF2m[C]∥IEEE International Symposium on Information Theory.IEEE,2014:2449-2453. [10] JIAO X,WEI H,MU J,et al.Improved ADMM Penalized Decoder for Irregular Low-density Parity-check Codes[J].IEEE Communications Letters,2015,19(6):913-916. [11] JIAO Xiaopeng,MU Jianjun.Lowering the Error Floor of ADMM Penalized Decoder for LDPC Codes[J].中国通信,2016(8):127-135. [12] DEBBABI I,GAL B L,KHOUJA N,et al.Comparison of Different Schedulings for the ADMM Based LDPC Decoding[C]∥International Symposium on Turbo Codes and Iterative Information Processing.IEEE,2016:51-55. [13] DEBBABI I,GAL B L,KHOUJA N,et al.Fast Converging ADMM-penalized Algorithm for LDPC Decoding[J].IEEE Communications Letters,2016,20(4):648-651. [14] LIU X,DRAPER S C,RECHT B.Suppressing Pseudocodewords by Penalizing the Objective of LP Decoding[C]∥Information Theory Workshop.IEEE,2012:367-371. [15] WANG B,MU J,JIAO X,et al.Improved Penalty Functions of ADMM Penalized Decoder for LDPC Codes[J].IEEE Communications Letters,2017,99:234-237. [16] FELDMAN J,MALKIN T,SERVEDIO R A,et al.LP Decoding Corrects a Constant Fraction of Errors[J].IEEE Transactions on Information Theory,2007,53(1):82-89. [17] HALABI N,EVEN G.LP Decoding of Regular LDPC Codes in Memoryless Channels[C]∥IEEE International Symposium on Information Theory Proceedings.IEEE,2010:744-748. [18] FELDMAN J,WAINWRIGHT M J,KARGER D R.Using Linear Programming to Decode Binary Linear Codes[J].IEEE Transactions on Information Theory,2005,51(3):954-972. [19] 陈紫强,欧阳缮,李民政,等.一种基于改进线性规划的LDPC码混合译码算法[J].电路与系统学报,2013(1):107-112. [20] LIU X,DRAPER S C.The ADMM Penalized Decoder for LDPC Codes[J].IEEE Transactions on Information Theory,2014,62(6):2966-2984. ConstructionMethodOptimizationBasedonADMMPenaltyFunction CHEN Zi-qiang,WANG Guang-yao (SchoolofInformationandCommunicationEngineering,GuilinUniversityofElectronicTechnology,GuilinGuangxi541000,China) In order to improve the error-rate performance and the converging rate for traditional ADMM penalized decoding algorithm,we further optimized the penalty function and proposed the TS-ADMM-PD algorithm based on three-segment penalty function.The algorithm introduced a transition function whose slope is between the front and rear one.And the function is applied to make a compromise on decoding performance and convergence rate.The optimized penalty function has a larger slope nearx=0 andx=1 to penalize the pseudo code word more heavily,so as to reduce the error rate and accelerate the converging speed.It has a smaller slope nearx=0.5 to make it easier to update the variables nodes information.Experimental simulation results show that the proposed TS-ADMM-PD algorithm has more excellent error-rate performance and converging speed than I-ADMM-PD algorithm. LDPC codes;ADMM;penalty function;error-rate performance;converging rate 10.3969/j.issn.1003-3106.2017.12.06 陈紫强,王广耀.基于ADMM的惩罚函数构造方法优化[J].无线电工程,2017,47(12):24-29.[CHEN Ziqiang,WANG Guangyao.Construction Method Optimization Based on ADMM Penalty Function[J].Radio Engineering,2017,47(12):24-29.] TN911.22 A 1003-3106(2017)12-0024-06 2017-06-22 国家自然科学基金资助项目(61461015);广西自然科学基金资助项目(2014GXNSFAA118399);广西教育厅科研基金资助项目(ZD2014052)。 陈紫强男,(1973—),博士,副教授,硕士生导师。主要研究方向:信号与信息处理、阵列信号处理、模式识别和信道编码识别分析等。 王广耀男,(1992—),硕士研究生。主要研究方向:信号与信息处理。

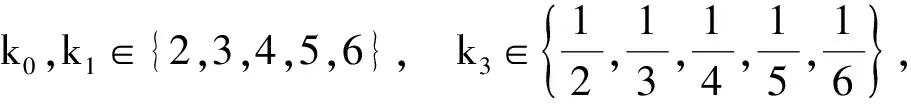
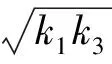
4 仿真结果及分析

5 结束语
