基于Laurent分解的GMSK定时同步环路
2017-11-07谢春磊
谢春磊,张 涛
(1.中国电子科技集团公司第五十四研究所,河北 石家庄050081;2.装备工程技术研究实验室,河北 石家庄050081;3.杭州海康威视数字技术有限公司,浙江 杭州310051)
基于Laurent分解的GMSK定时同步环路
谢春磊1,2,张 涛3
(1.中国电子科技集团公司第五十四研究所,河北 石家庄050081;2.装备工程技术研究实验室,河北 石家庄050081;3.杭州海康威视数字技术有限公司,浙江 杭州310051)
定时同步是数字调制信号接收不可或缺的环节。对于GMSK信号定时同步,现有算法多为数据辅助或前馈类算法。从GMSK信号的Laurent分解出发,结合Gardner定时同步环路,提出了一种基于Laurent分解的GMSK信号定时同步环路。该环路采用2 bit差分来提取定时误差,用于控制内插时刻,环路简单,运算量小,易于工程实现。仿真结果表明,即使对于小BT值GMSK信号,该方法依然可以有效提取定时误差,且具有较强的抗噪声性能。
定时同步;高斯最小频移键控;Laurent分解;Gardner算法
0 引言
高斯最小频移键控(GMSK)是一种连续相位调制(CPM)方式[1],其包络恒定、带外辐射小[2],因此,在GSM系统、无线局域网、航空数据链以及空间数据传输[3]等领域得到了广泛应用。GMSK解调分为相干解调和非相干解调[4]。相干解调的实现需要进行频偏和定时误差补偿,还需要进行载波相位同步[5],实现复杂度较大;非相干解调[6]主要有2类:差分方式[7]和限幅鉴频[8]方式,易于实现,但解调性能不如相干解调。
GMSK的解调无论采用哪种方式,都必须进行定时同步。数据辅助定时同步算法[9]的收敛速度快、性能好,但降低了系统传输效率;非数据辅助定时同步算法具有更普遍的适用性。非数据辅助类算法又可以分为前馈算法和反馈算法,前馈算法多是基于最大似然方法对定时误差估计[10-12],计算量大,并且无法实时跟踪定时误差的变化;反馈算法采用环路的方法,对定时误差进行实时检测、校正,实现简单。文献[13]对最小频移键控(MSK)类信号进行非线性变换,提取定时误差;文献[14]对差分后GMSK信号采用Gardner算法[15]进行定时误差提取,但当带宽周期积(BT)值较小时,误差值较小,算法性能不好。结合上述反馈算法原理,并考虑Laurent分解,在Gardner算法的基础上,本文改进了一种GMSK定时同步环路,其对BT值较小的GMSK也有很好的适用性。
1 Laurent分解
GMSK信号的CPM复基带形式为:
s(t)=exp(jδ(t,α)+jφ),
(1)
式中,φ为载波初始相位;δ(t,α)表示相位调制过程,可用式(2)表示:
nT≤t≤(n+1)T,
(2)
式中,h为调制指数,对于GMSK取值固定为0.5;{αk,k=0,1,…,n-1}是取值为±1的符号序列;T为符号周期;g(t)为高斯低通滤波器与持续时间为T的矩形脉冲卷积结果,其形式为:
(3)
(4)
式中,B为高斯滤波器3 dB带宽;Q(t)为互补误差函数。
g(t)的主要能量集中在L个符号周期内[16],L的大小由BT值决定,BT越小,L越大,则信号的码间串扰越严重,对于BT=0.3,可以取L=3,并且g(t)满足
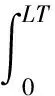
(5)
s(t)通过加性高斯白噪声信道传输后接收到的信号复包络可表示为:
r(t)=exp{j[2πΔft+δ(t-εT,α)+φ]}+z(t),
(6)
式中,Δf为载波频偏,其主要由多普勒频移、收发两端载波偏差引入;εT为定时偏差;z(t)为接收端噪声。
按照Laurent分解理论,CPM信号可以表示为M=2L-1个脉冲幅度调制(PAM)信号之和,形式为:
(7)
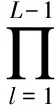
(8)
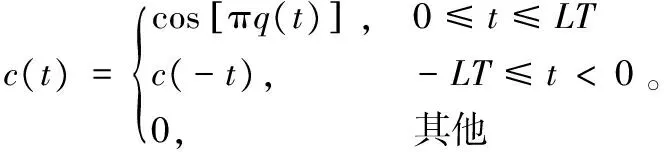
(9)
γm,l的取值为0或1,并且满足
(10)

(11)
伪符号序列αm,i满足
(12)
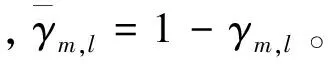
通过计算可以获得各个PAM分量的波形,以BT=0.3,L=4的GMSK信号为例,h0(t)、h1(t)、h2(t)三个幅值较大的PAM波形如图1所示。
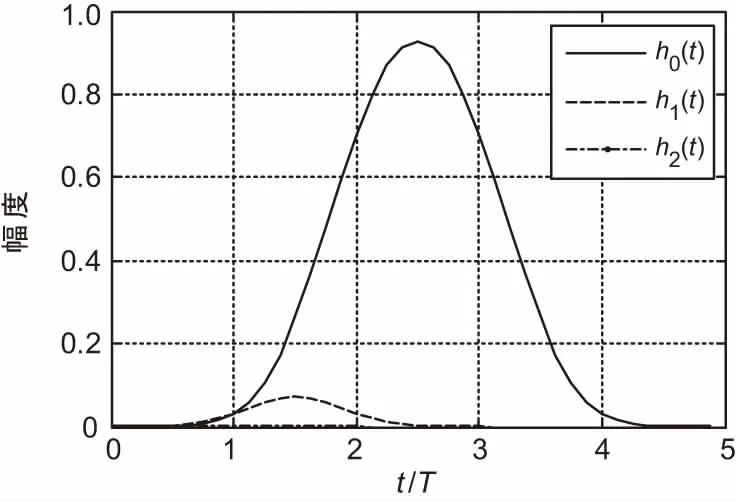
图1 BT=0.3的GMSK信号PAM分量
可以看出,h0(t)的幅度最大,并且占了信号总能量的99%以上。因此,可以仅用h0(t)来近似GMSK信号,从而有
(13)
(14)
由式(14)可以看出,i为偶数时,α0~α1的累加和为偶数;i为奇数时,α0~α1的累加和为奇数,即
(15)
(16)
式(13)可以改写为:

(17)
可以看出,信号形式与OQPSK信号类似,I路和Q路存在一个符号周期的偏差。
2 定时同步算法
由图1可知,虽然h0(t)的持续时间为5个符号周期,但仅有中间4个符号周期的幅度较大,因此可以将其截短为4个符号周期,这时I/Q两路波形如图2所示。
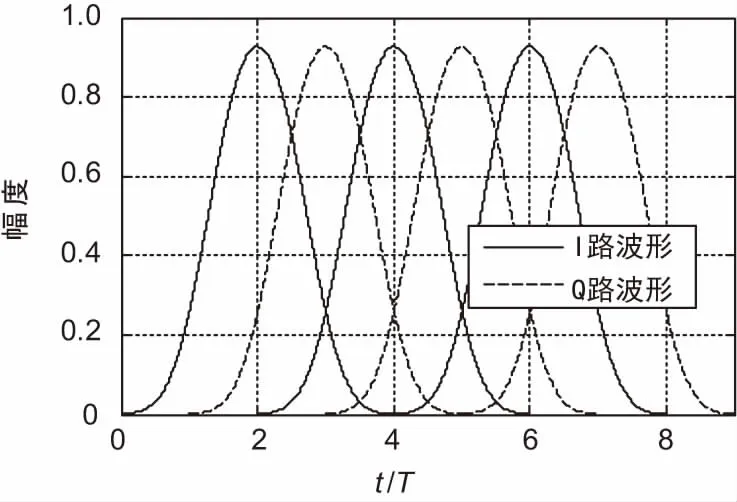
图2 I/Q两路PAM分量示意
按照2个符号周期的间隔,对s(t)进行差分,并取其平方的实部,得
c(t)=Re{[s(t)s*(t-2T)]2}。
(18)
如图2所示,当t在2iT附近时,Q路波形很小,仅有I路波形,且t偏离2iT的距离越大,幅度越小,因此c(t)是|t-2iT|的单调递减函数;同理,当t在(2i+1)T附近时也具有该特性,从而c(t)的期望是周期为T的周期函数[17]。按照式(17),计算E{c(t)}得到图3,具有对称特性。
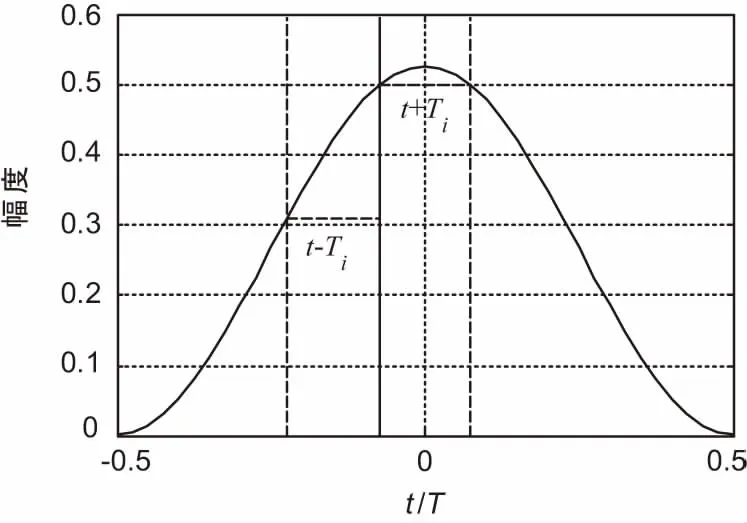
图3 代价函数c(t)的期望
考虑以下定时误差提取公式:
e(t)= -c(t-Ti)+c(t+Ti)=
-Re[s2(t-Ti)s*2(t-Ti-2T)]+
Re[s2(t+Ti)s*2(t+Ti-2T)]。
(19)
观察图3,当t=0时,由于其对称性,c(t-Ti)=c(t+Ti),误差e(t)=0;而当t<0时,c(t-Ti)
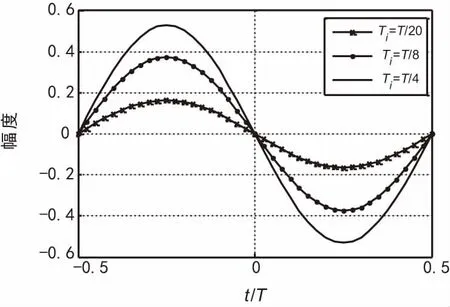
图4 误差提取公式e(t)的S曲线
3 算法实现
按照软件无线电的思想,对A/D采样后的数据进行内插,将信号内插为4倍符号速率,采样间隔Ts=T/4。按照式(19)所示误差提取公式及图4所示的S曲线,选定Ti=Ts,此时S曲线的幅度最大。参照Gardner定时环路的原理[18],将定时误差检测结果通过环路滤波,进行平滑处理,控制NCO,内插出最佳采样点数值[19-20]。GMSK定时同步环路结构如图5所示,定时误差检测的数据流图如图6所示。
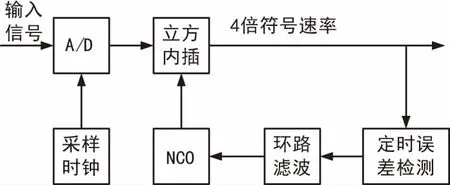
图5 GMSK定时同步环路结构
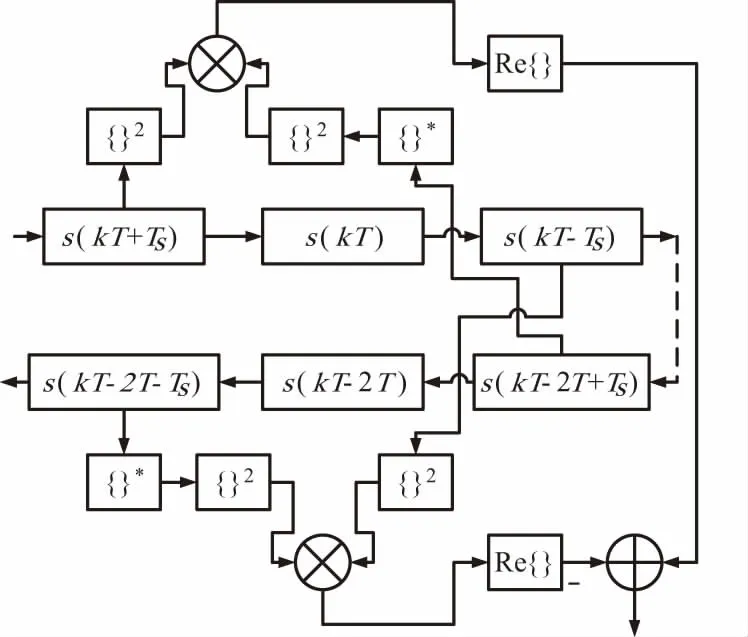
图6 定时误差检测数据流
4 性能仿真及分析
性能仿真从以下4个方面来分析、比较本文的定时同步算法:① 不同BT值对应的S曲线;② 定时误差检测算法的抗频偏性能;③ 不同信噪比下定时收敛性能;④ 与文献[13-14]的定时误差检测性能进行比较。
4.1 不同BT值对应的S曲线
在不同的BT值下,GMSK信号有不同的频谱特性,BT值越小,带宽效率越高,相应接收复杂度也越大,好的定时同步算法不仅要适用于大BT值信号,也要适用于小BT值信号。令BT值分别为0.2、0.3、0.5,另外BT值趋于无穷时即为MSK信号,图7分别给出了其定时误差检测S曲线。可以看出,在相同定时偏差下,BT值越小,定时误差越小。这是因为随着BT值的减小,Laurent分解中h0(t)分量所占的比例相应降低,用式(13)进行简化带来的失真将增大,从而导致定时误差值减小。
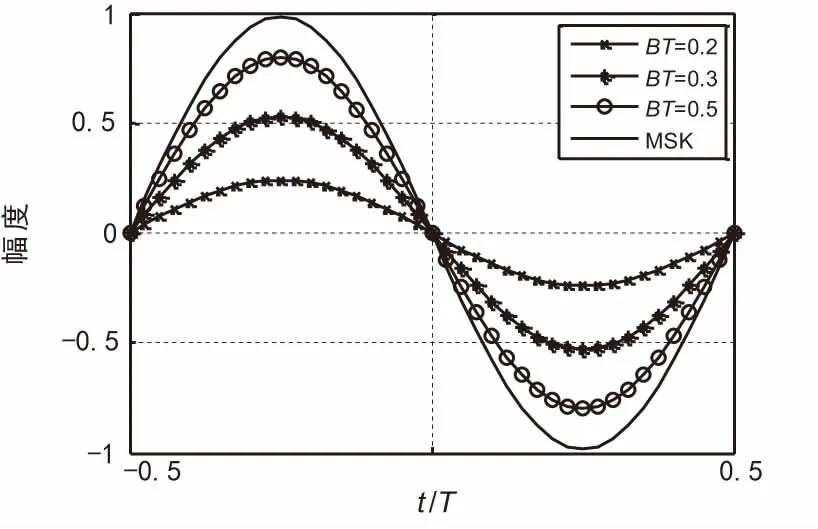
图7 不同BT值对应的S曲线
4.2 定时同步的抗频偏性能
定时同步受频偏的影响越小,接收机的抗频偏性能也就越好,该环路的工程应用价值越高。以BT=0.3的GMSK信号为例,设定频偏fc与符号速率Rs的相对值分别为0、1%、3%、5%时,其中Rs=1/T,其定时误差检测S曲线如图8所示。
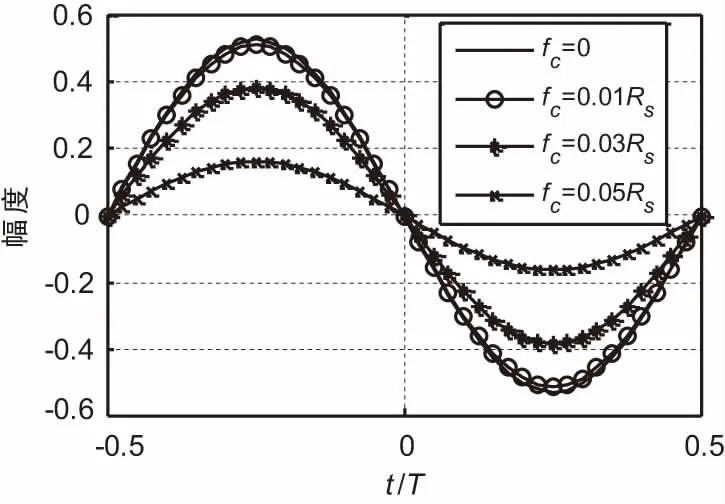
图8 不同频偏值的S曲线
fc在1%Rs以内时,S曲线基本没有变化;fc继续增大时,定时误差值变小,性能变差。
4.3 不同信噪比下定时收敛性能
随着信噪比的降低,定时环路的收敛速度会变慢;但好的误差提取算法可以在更低的信噪比下达到收敛。以BT=0.3、频偏为1%Rs的GMSK信号为例,分别取Eb/N0=5 dB、10 dB、20 dB,其定时误差收敛曲线如图9所示。可以看出,信噪比越低,收敛速度越慢;同时,环路在Eb/N0=5 dB时仍然可以达到收敛,可以实现低信噪比信号的解调。
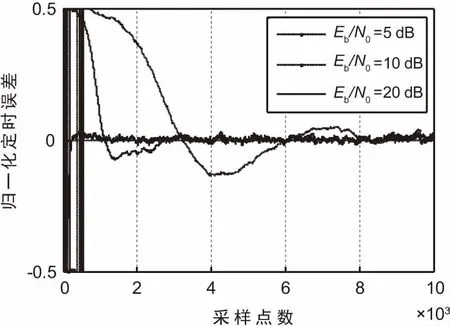
图9 不同信噪比下定时误差收敛曲线
4.4 与现有算法的比较
将本文的算法分别与文献[13-14]进行比较,对比其定时误差检测性能。以BT=0.3的GMSK信号为例,其定时误差S曲线如图10所示。可以看出,在相同定时误差下,本文算法具有更大的误差值,可以获得更快的收敛特性、更好的抗噪特性。
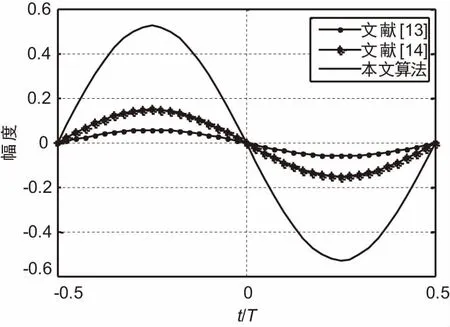
图10 本文S曲线与文献[13-14]的比较结果
5 结束语
本文从GMSK信号的Laurent分解入手,从现有差分检测类定时同步算法的原理出发,并与常用定时同步环路相结合,提出了一种改进的GMSK信号定时同步环路。与现有算法相比,具有更好的定时误差检测性能,而且对小BT值GMSK信号也有很好的检测性能。该同步方法对现有环路的改动不大,因此可以很好地应用于工程实践。
[1] LAURENT P A.Exact and Approximate Construction of Digital Phase Modulations by Superposition of Amplitude Modulated Pulses(AMP)[J].IEEE Trans.Commun.,1986,34(2):150-160.
[2] MORUTA K,HIRADE K.GMSK Modulation for Digital Mobile Radio Telephony[J].IEEE Trans.Commun,1981,29(6):1044-1050.
[3] 游莎莎,刘胜利,罗雷刚,等.GMSK调制技术及其在遥测中的应用分析[J].无线电工程,2011,41(12):41-43.
[4] HUANG Y L,FAN K D,HUANG C C.A Fully Digital Noncoherent and Coherent GMSK Receiver Architecture with Joint Symbol Timing Error and Frequency Offset Estimation[J].IEEE Trans.Veh.Technol.,2000,49(3):863-874.
[5] 彭华.软件无线电中的盲接收技术研究[D].郑州:解放军信息工程大学,2002:123-148.
[6] 吴伟仁,节德刚,丁兴文,等.深空测控通信中GMSK体制非相干解调算法研究[J].宇航学报,2014,35(12):1437-1443.
[7] SIMON M K,WANG C C.Differential Detection of Gaussian MSK in Mobile Radio Environment[J].IEEE Transactions on Vehicular Technology,1984,33(4):307-320.
[8] KORN I.GMSK with Limiter Discriminator Detection in Satellite Mobile Channel[J].IEEE Transactions on Communications,1991,39(1):94-101.
[9] 吴玉成,陈亮,李国权.GMSK中频数字化非相干接收机的设计与实现[J].无线电工程,2008(03):58-60.
[10] MICHELE M,UMBERTO M.Joint Frequency and Timing Recovery for MSK-type Modulation[J].IEEE Trans.Commun.,1999,47(6):938-946.
[11] 赵民建,仇佩亮,李国纲.一种软件无线电GMSK非相干接收机[J].电路与系统学报,2003,8(5):127-131.
[12] 赖文强,赵建业.一种面向DSP实现的GMSK位同步算法[J].无线电工程,2004,34(2):12-14.
[13] ALDO N D A,UMBERTO M,RUGGERO R.A Digital Approach to Clock Recovery in Generalized Minimum Shift Keying[J].IEEE Trans.Veh.Technol.,1990,39(3):227-234.
[14] AZAM M,AKRAM E,AHMAD J,et al.An Improved,Non-data Aided Symbol Timing Recovery for GMSK Modulated Signals[C]∥Islamabad:MultiTtopic Conference,2004:107-111.
[15] GARDNER F M.A BPSK/QPSK Timing Error Detector for Sampled Receivers[J].IEEE Trans.Commun.,1986,41(5):998-1008.
[16] 张辉,曹丽娜.现代通信原理与技术[M].西安:西安电子科技大学出版社,2002:273-276.
[17] 程芹,陈伟,龙必起,等.一种改进的定时误差检测算法[J].电视技术,2011,35(11):108-111.
[18] 付永明,朱江,琚瑛珏.Gardner定时同步环路参数设计及性能分析[J].通信学报,2012,33(7):191-198.
[19] 熊志珲,赵晓群.基于分段抛物线滤波器的GMSK定时恢复方法[J].大连民族学院学报,2010,12(5):440-442.
[20] 黄凌.一种基于非线性差分运算的MSK定时同步环路[J].四川兵工学报,2014,35(3):119-121.
ADigitalTimingTrackingLoopBasedonLaurentRepresentationforGMSKModulations
XIE Chun-lei1,2,ZHANG Tao3
(1.The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China; 2.EquipmentEngineeringTechnologyResearchLaboratory,ShijiazhuangHebei050081,China; 3.HangzhouHikvisionDigitalTechnologyCo.Ltd,HangzhouZhejiang310051,China)
Timing synchronization is an indispensable part in receiving digital modulation signal.Most of the existing algorithms for the timing synchronization of GMSK signals are either data aided or feed forward.In this paper we present a digital timing tracking loop for GMSK modulations.This technique is based on Laurent representation and combined with Gardner timing recovery loop.The loop gets the timing error based on two bit differential detection,and then controls the interpolating.The loop is simple,has little computational complexity,and can be easily implemented.Simulation results show that the timing error can be efficiently extracted even for GMSK with small BT,and the loop has a fine anti-noise performance.
timing synchronization;GMSK;Laurent representation;Gardner algorithm
10.3969/j.issn.1003-3106.2017.12.05
谢春磊,张涛.基于Laurent分解的GMSK定时同步环路[J].无线电工程,2017,47(12):20-23,60.[XIE Chunlei,ZHANG Tao.A Digital Timing Tracking Loop Based on Laurent Representation for GMSK Modulations[J].Radio Engineering,2017,47(12):20-23,60.]
TN911
A
1003-3106(2017)12-0020-04
2017-01-11
国家部委基金资助项目。
谢春磊男,(1984—),工程师。主要研究方向:数字调制信号解调、分析。
张涛男,(1986—),工程师。主要研究方向:计算机视觉、机器学习和人工智能等信号处理相关算法。
