半潜式钻井平台复合锚泊系统组分配比优化设计

2017-11-07陈国明刘正礼盛积良

海洋工程 2017年5期

罗宁，张浩, 2，宋强, 2，陈国明，刘正礼，盛积良

(1.中国石油大学(华东) 海洋油气装备与安全技术研究中心，山东青岛 266580; 2.中国船舶科学研究中心，江苏无锡 214082; 3.中海石油(中国)有限公司深圳分公司，广东深圳 518067)

罗宁1，张浩1, 2，宋强1, 2，陈国明1，刘正礼3，盛积良1

从提高锚泊系统收放时效性入手，提出了一种半潜式钻井平台复合式锚泊系统组分配比优化设计方法，旨在尽可能降低复合式锚泊系统的钢链配比长度，提高收放效率。结合锚泊系统设计参数，制定优化设计准则，建立优化分析流程，采用ANSYS-AQWA建立锚泊定位半潜式平台水动力分析模型，获得平台运动参数和锚链动力参数，对平台漂移量、锚链最小安全系数、走锚临界张力、锚链最小卧底长度和起锚力进行无量纲指标分析，并综合考虑张力倾角与预张力对优化结果的影响，获得复合式锚泊系统钢链与钢缆的最优配比关系，确定最优钢链长度为395 m，较原钢链长度缩短225 m，钢链收放时间降低36%，进一步提高锚泊系统收放时效性,并降低平台可变荷载。

复合式锚泊系统；优化设计；半潜式钻井平台

随着国际油价的迅速回落，降本增效已成为石油行业的重中之重。然而深水油气勘探一直都是高投入工程[1]，如何合理地降低海洋石油的开发成本，已成为当下石油行业最关注的问题。目前锚泊定位的深水半潜式钻井平台所使用的钢链长度较大，与钢缆相比，钢链的下放与回收效率极低。因此，从降低海洋石油勘探开发的能耗成本与时间成本出发，在保证原有锚泊性能的前提下，尽可能降低钢链的配比长度，既能够提高锚泊系统的收放效率，又可以缓解海洋钻井平台可变荷载冗余量小的问题。

Matthias Brommundt[2]对海上半潜式风力发电设备的悬链线系泊系统进行优化设计，使用Nelder-Mead单一算法优化锚链系泊线长度，使成本达到最低。Mir Emad Mousavid等[3-4]从完整性管理角度出发提出了一种简单的工程分析方法，针对完整性和设计极限分别提出了优化算法，将该方法应用到锚泊系统设计与优化分析上，并对锚泊系统的不同组分进行了可靠性分析。Ayhan Mentes等[5]采用模糊层次分析法建立数学模型，针对锚泊系统的选型提出了一种设计方法，并结合该方法对不同选型方案进行案例敏感性分析。Mehdi Shafieefar等[6]采用遗传算法，在考虑环境荷载传递情况下，对平台朝向和锚泊系统选型进行优化，并考虑锚链材料属性和尺寸，对单根锚链进行线长和预张力的优化分析。Aline Aparecidade Pina等[7]采用人工神经网络方法对浮式结构的锚泊系统进行分析，通过考虑水深、平台与立管参数等，建立锚泊定位平台的设计方法，并说明其方法对任意悬链线系泊系统均具有普适性。Klingan K E[8]以经济性与可变性为目标，考虑实际环境参数，基于非单调线性搜索的二次序列规划法，采用Marintek开发的SIMA软件对锚泊系统进行优化分析。

余龙等[9-10]利用准静定法推导多组分锚泊悬链线方程，并采用遗传算法对“南海2号”钻井平台锚泊系统进行优化分析。周洋[11]对多组分悬链线锚泊系统进行设计与优化，结合准静定分析，形成锚泊系统响应的时域计算方法。樊磊，孙丽萍等[12]以满足安全要求，确保良好水动力性能为目标，采用时域方法对半潜式起重平台的锚泊系统进行优化研究。李亚男等[13]采用AQWA-iSight联合计算，以平台的垂荡、纵荡及横摇响应为约束，得到最优系泊缆长度。王宽[14]将锚链方位角和抛锚距离作为变量，以考虑各浪向发生概率的加权平动位移为优化目标，采用遗传算法对该优化问题进行求解。石建峰等[15]采用非线性规划算法进行锚链张力优化，并对981钻井平台进行仿真分析，结果符合安全作业要求。

按照深水半潜式钻井平台的起抛锚作业流程，本文对现役平台的复合式锚泊系统进行二次优化设计，提出一种深水半潜式钻井平台复合式锚链长度配比优化设计方法，并结合工程实例建立复合式锚泊系统动力分析模型，对锚链长度的配比进行优化设计，旨在缩短起抛锚作业时间，减少作业租金，增大平台可变载荷余量，降低作业成本，提高作业效率。

1 复合式锚泊系统动力分析模型

锚泊定位半潜式平台由平台本体和复合式锚泊系统两部分组成，图1为锚泊状态下深水半潜式钻井平台的示意图。这两部分之间存在耦合作用，并在风、浪、流的作用下产生运动。锚链作为约束条件，为平台提供回复力，使其在外界环境作用下不产生大的位移，以保证整个钻井系统的安全性。在产生回复力的同时，锚链自身会存在轴向张力，当张力过大时，会导致走锚、起锚或者锚链的破坏。

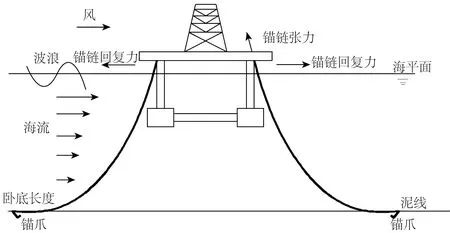
图1 锚泊状态下深水半潜式钻井平台示意Fig.1 Moored semi-submersible platform

在对锚链长度配比优化设计时，需要对锚泊状态下的半潜式平台进行动力分析，确定平台对锚泊系统施加的动边界条件。在风、浪、流共同作用下，平台的运动方程[16]：

式中：M为平台质量，C为阻尼系数，K为平台系泊刚度，Fwind为风力，Fcurrent为海流力，Fwave为波浪力，Fmoor为系泊力。

在确定平台运动后，以锚链为研究对象，对其进行动力分析，图2为锚链受力分析示意图。随着平台的运动，锚链线的张力倾角不断发生变化，导致锚泊系统回复力随时间变化[14]。

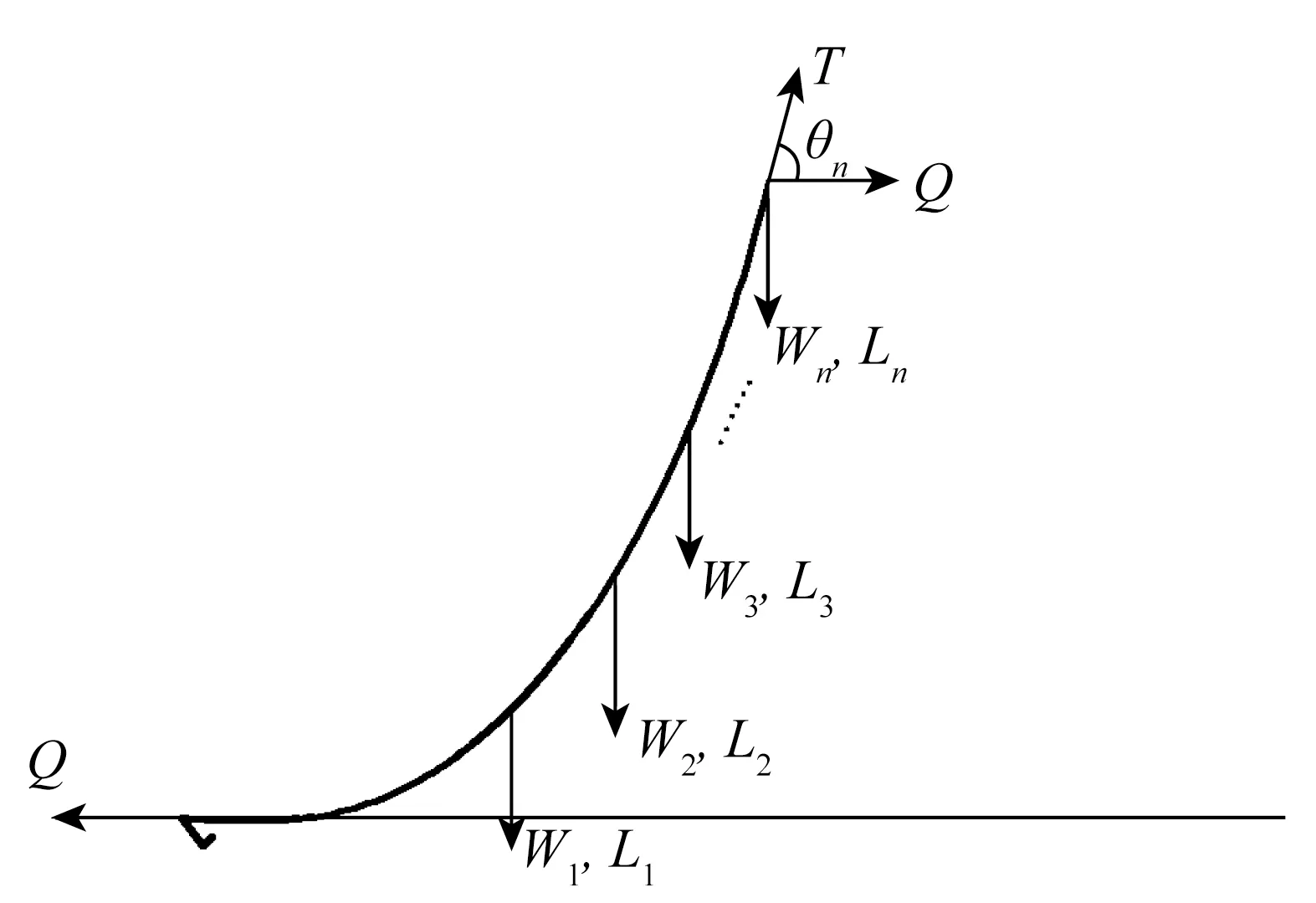
图2 复合式锚链受力示意Fig.2 Force of composite mooring system

式中：Q(t)为锚链的回复力，Wk为锚链第k组分的重度，Lk为锚链第k组分的长度，θk(t)为锚链第k段的水平倾角。

由于平台动边界条件影响，锚链在轴向上会产生动张力，动张力水平分量即为回复力，锚链的动张力与回复力的关系如下所示[14]：

式中：T(t)为锚链的动张力。

锚链回复力由锚抓力和卧底钢链的摩擦力组成，悬链线卧底长度既影响锚链的回复力大小，也决定锚泊系统与海底摩擦段的长度。根据悬链线方程可以得到悬链线长度计算公式，通过悬链线长度与锚链的抛出长度，可以确定锚链的卧底长度[14]：

式中：Lc(t)为悬链线长度，L为锚链总长度，Ld(t)为卧底链长度。

当锚链所承受水平拉力大于其临界回复力时，即发生走锚[17-18]。综合考虑锚抓力和卧底锚链的摩擦力，可计算得到走锚临界力[19]：

式中：Prmax(t)为走锚临界张力，Hr为锚在空气中质量为10 000磅时的抓力，Wa为锚在空气中的质量，b为基于底质的系数，λc为卧底链抓力系数，ωc为卧底链单位长度重量，Ld(t)为卧底链长度。

如图3所示，当平台运动位移过大时，迎流向锚链的卧底部分将被拉起，与海底泥面成一定夹角，进而对拖曳锚产生斜向起锚力，为简化分析模型，忽略入泥钢链与土体的摩擦作用，将受力分析点确定在泥线处，可得到拖曳锚所受斜向起锚力：

式中：θ0为锚链与泥线夹角，Fup(t)为垂向上拔力，Fu为斜向起锚力。

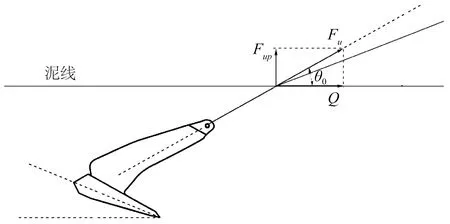
图3 拖曳锚起锚力示意Fig.3 Uplift force of anchor

2 复合式锚链长度优化配比准则与优化分析流程

深水半潜式钻井平台锚链长度配比优化的目标为：在保证原有系泊能力的前提下，最大限度地降低复合式锚泊系统中的钢链长度，以提高起抛锚作业效率。考虑到平台的作业安全性以及锚链自身的安全性，分别从平台的漂移量，锚链的动张力、锚链的走锚临界力、锚链的卧底长度和锚的起锚极限承载力五个方面进行分析，并制定优化设计准则。

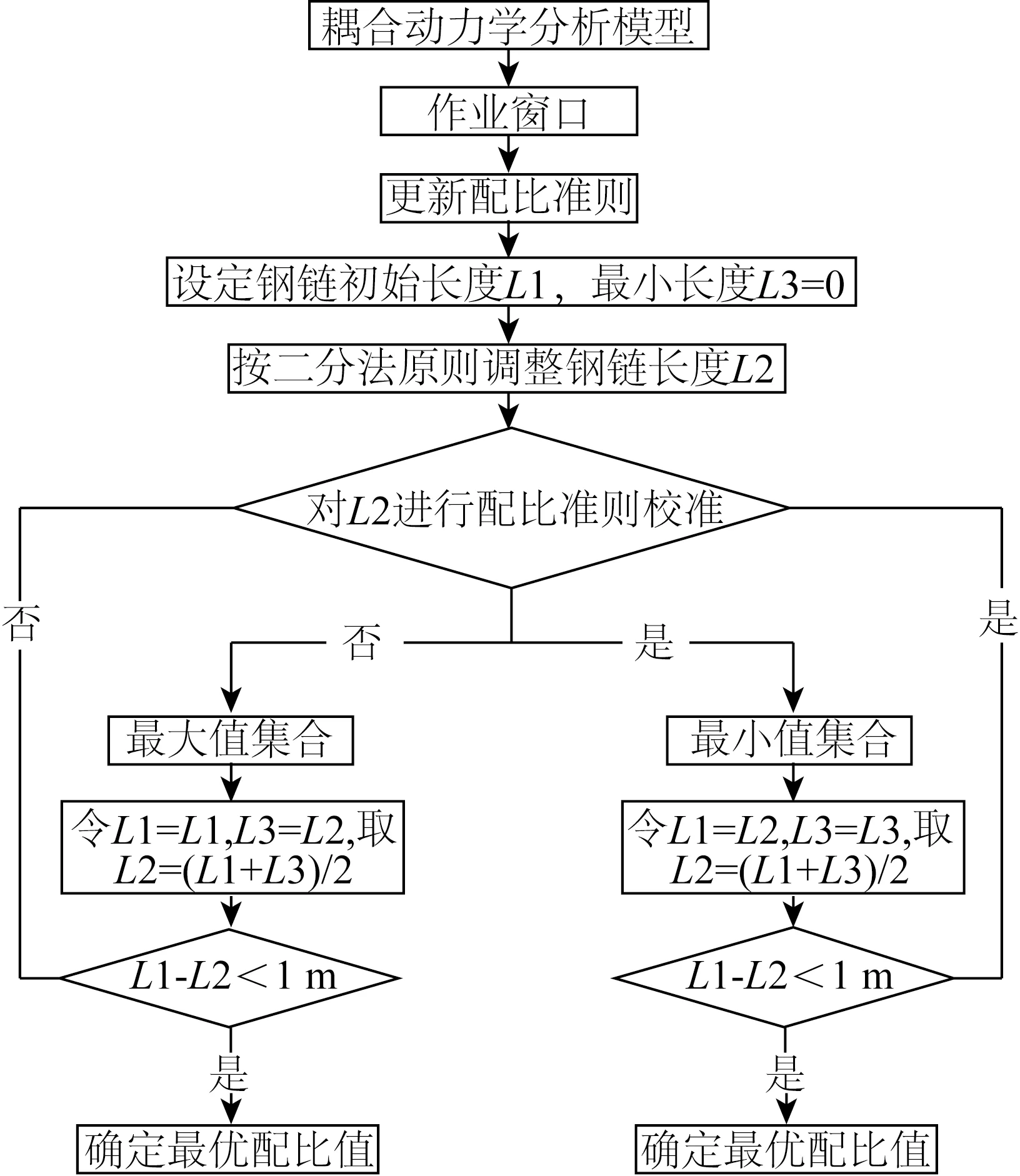
图4 复合式锚链长度配比优化分析流程Fig.4 Flow chart of optimization analysis for composite mooring system components

优化设计准则具体内容如下：

a) 缩短钢链长度后，锚泊系统对平台漂移量的控制能力不降低，即漂移量仍满足API规范要求[20]；

b) 缩短钢链长度后，锚泊系统的安全性符合规范要求，即完整状态下锚链最小安全系数不小于1.67[20]；

c) 缩短钢链长度后，锚泊系统的卧底长度小于钢链总长度，确保缆绳不与海床发生直体磨损(粘着磨损)[21-23]，降低缆绳与海底摩擦引起的失效概率；

d) 缩短钢链长度后，锚泊系统在作业工况下不发生走锚，避免因走锚造成海损事故[24-25]；

e) 缩短钢链长度后，拖曳锚所受斜向起锚力仍小于所用拖曳锚的极限承载力。

为快速得到最优的锚链长度配比关系，设计了锚链长度配比优化分析方法。在确定平台的最大作业窗口后，基于二分法原理，不断缩小满足准则的长度配比范围，以确定最优的锚链长度配比关系，具体分析流程如图4所示。

3 复合式锚链长度配比优化分析实例

3.1分析模型基本参数

以某深水半潜式平台的复合式锚泊系统为研究对象，采用ANSYS-AQWA建立耦合动力学分析模型，平台及锚泊系统基本参数见表1～表3。针对最大设计工作水深进行锚链长度配比优化，故优化后的锚泊系统同样适用于较浅海域。

表1 平台基本参数Tab.1 Parameter of platform

表2 锚链材料属性Tab.2 Material properties of mooring system

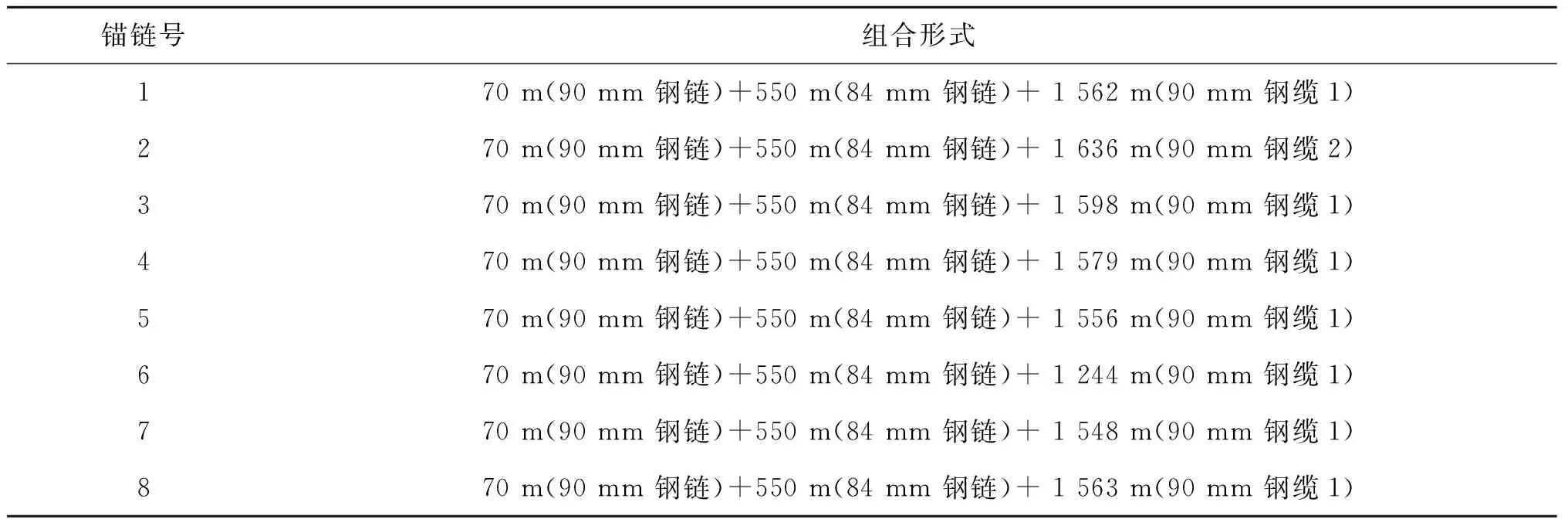
表3 复合锚链初始组合形式Tab.3 Initial parameter of composite mooring system

3.2复合式锚链长度配比优化分析

通过对原有平台-锚泊系统耦合模型进行动力分析，确定其最大作业工况，工况参数见表4，并以此为基础，进行锚链长度配比优化设计。

表4 最大作业工况Tab.4 Maximum operating environment

由表3可知，该锚泊系统的钢链原长度为620 m，根据既定分析方法和分析流程，对复合式锚链长度配比进行优化设计，得到各无量纲参数随钢链减少量的变化关系，并将无量纲参数与标准值1相比较，如图5所示，其中参数无量纲化见式(8)～(13)所示。

无量纲平均漂移量系数=平台平均漂移量/4%平台作业水深

(8)

无量纲最大漂移量系数=平台最大漂移量/ 8%平台作业水深

(9)

无量纲安全系数=锚链安全系数最小值/1.67

(10)

锚链卧底长度无量纲参数=锚链卧底长度/优化后所剩钢链总长度

(11)

走锚无量纲参数=最大动张力/临界锚泊力

(12)

起锚力无量纲参数=最大起锚力/拖曳锚极限承载力

(13)

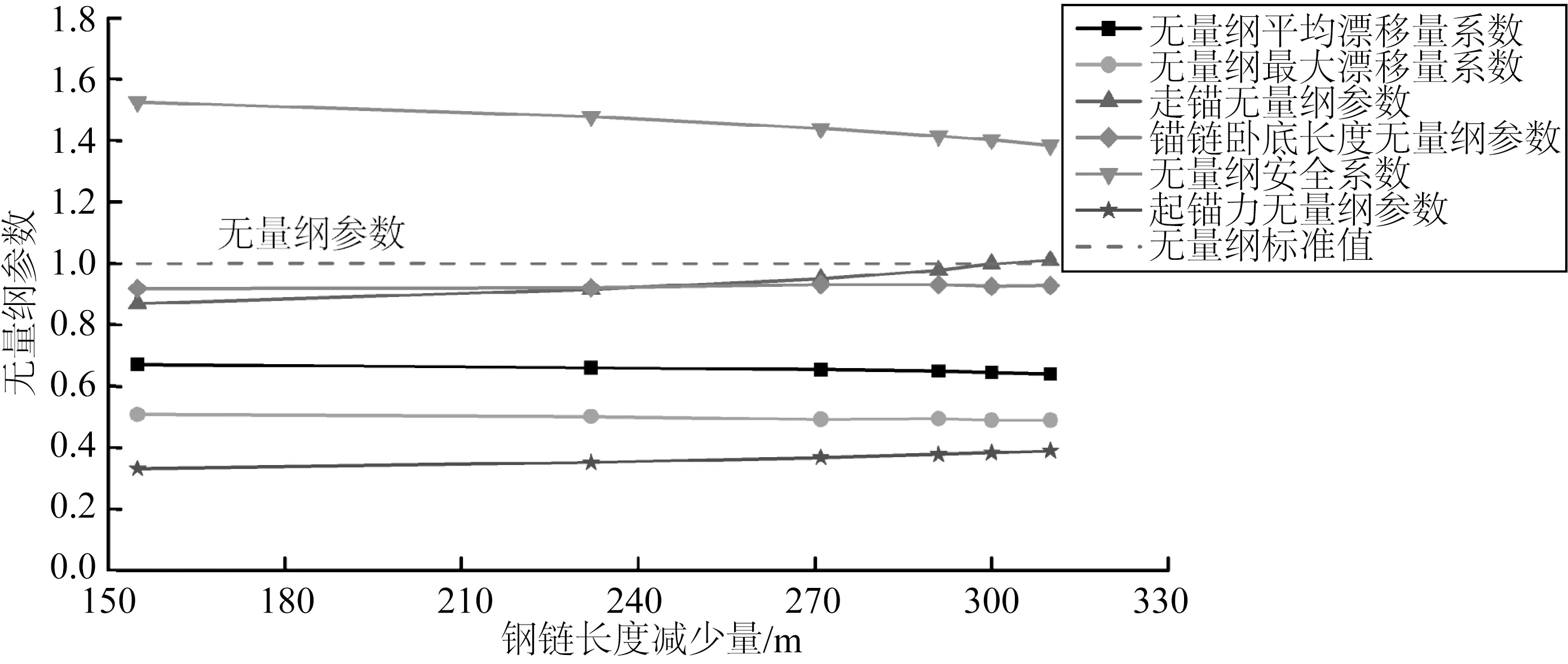
图5 各无量纲参数对钢链减少量的影响Fig.5 Effect of dimensionless parameters on steel chain reduction

由图5可知，随着锚泊系统钢链长度减少量的增加，走锚无量纲参数成为控制钢链配比长度的关键因素。当钢链减少量达到300 m时，走锚无量纲系数超过标准值1，说明在该种条件下，锚泊系统发生走锚，不符合优化设计要求，最终钢链减少量应保证在300 m以下。

4 不同参数对钢链减少量的影响

考虑到锚泊系统的张力倾角与预张力不是一成不变的，其变化量对锚泊系统的悬链线形状影响较大，因此，在原优化配比结果的基础上，结合张力倾角与预张力的变化适当增大钢链冗余量。

通过控制变量，分别获得不同张力倾角和预张力条件下钢链的最大减少量，可以看出，当张力倾角增大后，钢链的减少量呈先增大后减小的非线性趋势，而钢链减少量随锚链预张力增大呈线性减小趋势，具体结果如图6和图7所示。

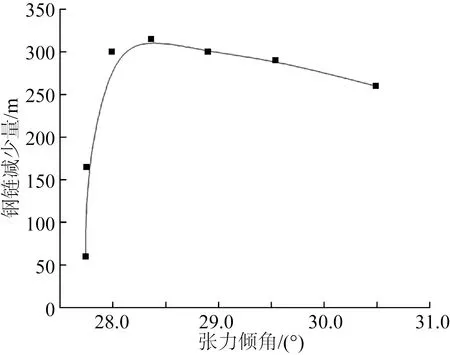
图6 张力倾角对钢链减少量的影响Fig.6 Effect of pretension angle on steel chain reduction

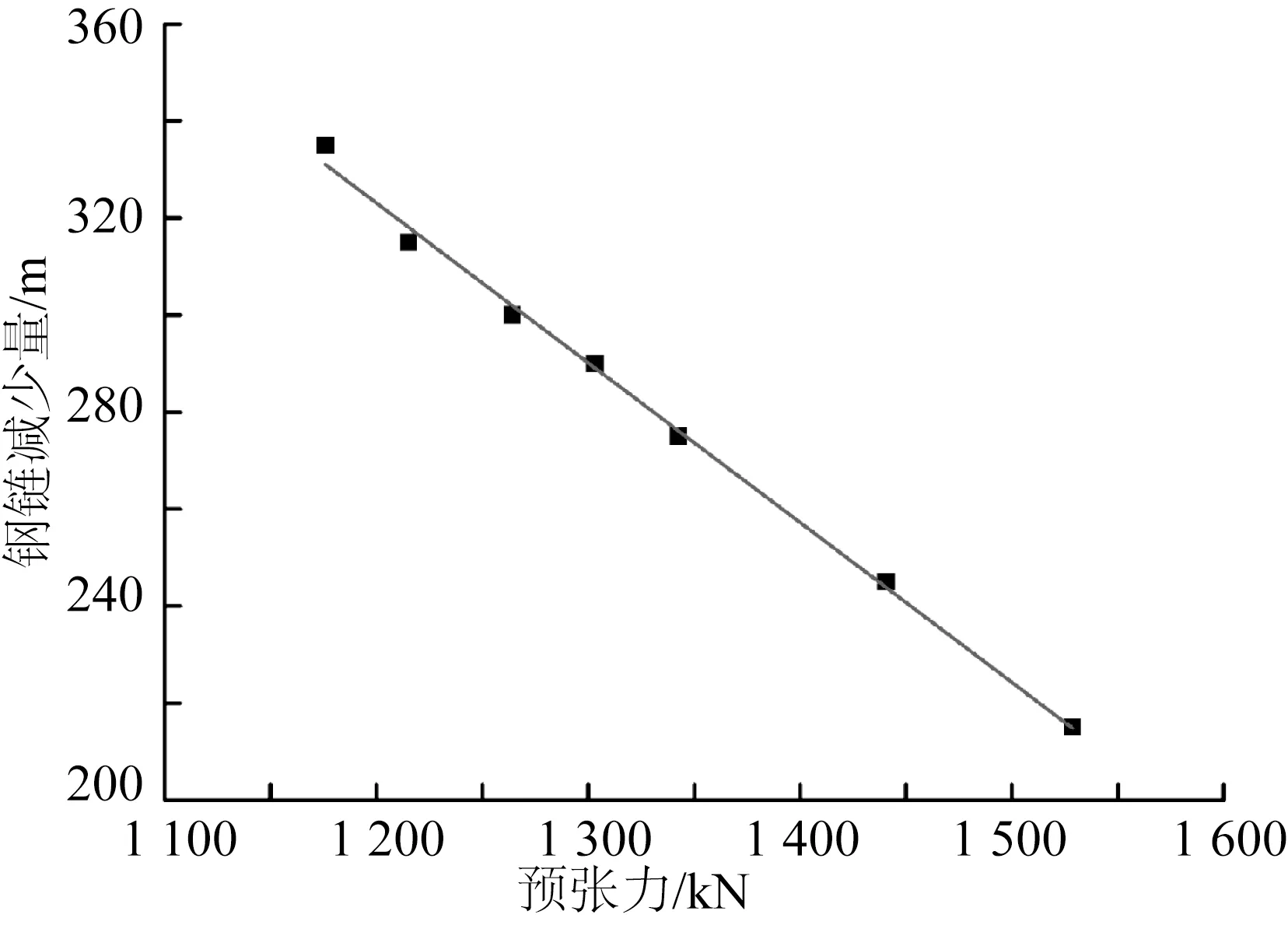
图7 预张力对钢链减少量的影响Fig.7 Effect of pretension on steel chain reduction

锚泊系统原有设计预张力为1 264.2 kN，张力倾角为27.8°，考虑锚链张力倾角实际误差为±1°，预张力实际误差为±100 kN，为保证锚泊系统具有充足的钢链长度，在原有优化结果基础上，增加25%的安全冗余，综合考虑二者对钢链减少量的影响，钢链最优减少量确定为225 m。根据上述计算结果，确定锚链长度配比的最终值，具体参数见表5所示。

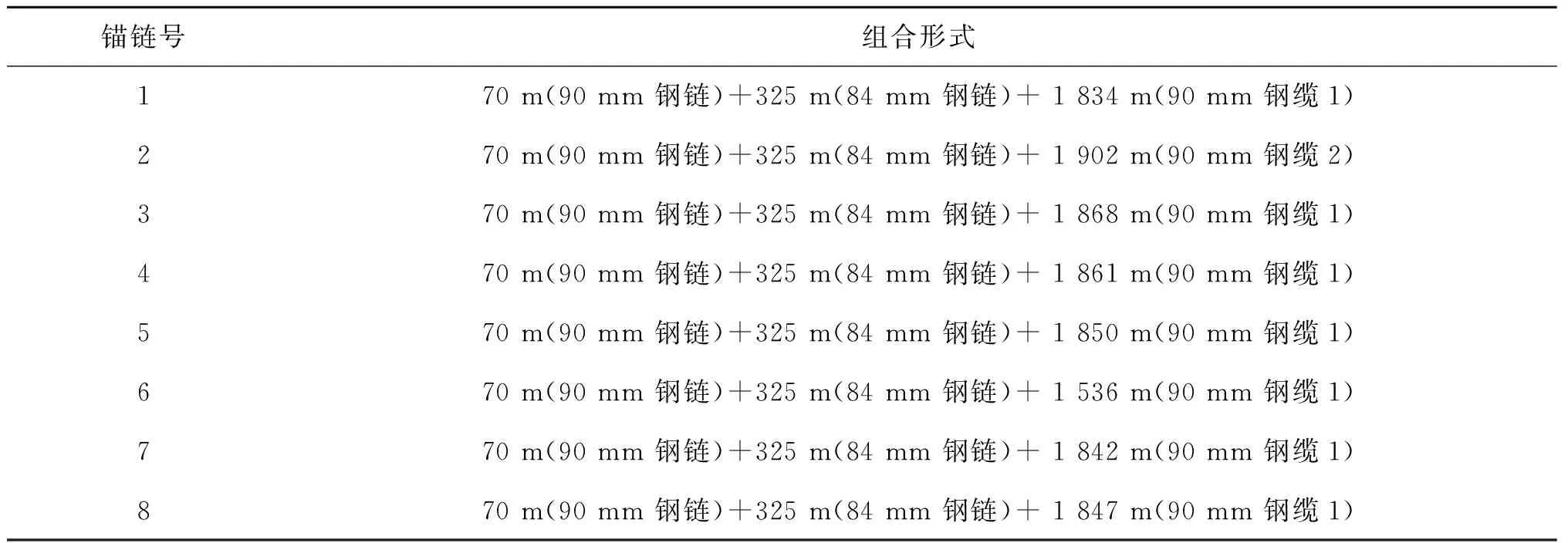
表5 最终锚链长度配比Tab.5 Optimization results of composite mooring system

5 结语

1) 结合现场实际作业要求提出锚链长度配比优化问题，并针对该问题提出五项优化设计准则及分析流程。通过实例计算，确定该分析方法与流程的可行性。

2) 根据分析实例可知，现有半潜式钻井平台锚泊系统的钢链长度具有较大的调整弹性。该模型可以在原有锚链基础上将钢链长度缩短255 m，占原有钢链长度的36%，同时锚链总重量降低约189 t，有效降低了锚泊系统对平台可变载荷的影响，说明优化结果具有较好的工程意义。

3) 进行优化结果对张力倾角和预张力的敏感性分析，分析结果表明，锚链长度配比优化结果对张力倾角和锚链预张力的变化十分敏感，应结合二者的影响对优化结果进行二次修正。

[1] 鞠少栋，畅元江，陈国明，等.深水钻井隔水管连接作业窗口分析[J].石油勘探与开发，2012，39(1)：105-110.(JU Shaodong,CHANG Yuanjiang,CHEN Guoming,et al.Envelopes for connected operation of the deepwater drilling riser [J].Petroleum Exploration and Development,2012,39(1): 105-110.(in Chinese))

[2] MATTHIAS Brommundt,LUDWING Krause,KARL Merz.Mooring system optimization for floating wind turbines using frequency domainanalysis[J].Energy Procedia,2012( 24): 289-296.

[3] MIR Emad Mousavi,PAOLO Gardoni.A simplified method for reliability and integrity-based design of engineering systems and its application to offshore mooring system[J].Marine Structures,2014(36): 88-104.

[4] MIR Emad Mousavi,PAOLIO Gardoni,MEHDI Maadooliat.Progressive reliability method and its application to offshore mooring systems[J].Engineering Structures,2013(56): 2 131-2 138.

[5] AYHAN Mentes,ISMAIL Hakki Helvacioglu.Fuzzy decision support system for spread mooring system selection[J].Expert Systems with Applications,2012(39): 3 283-3 297.

[6] MEHDI Shafieefar,AIDIN Rezvani.Mooring optimization of floating platforms using a genetic algorithm[J].Ocean Engineering,2007,34(10):1 413-1 421.

[7] ALINE Aparecidade Pina,BRUNODA Fonseca Monteiro,CARL Horst Albrecht,et al.Artificial neural networks for the analysis of spread-mooring configurations for floating production systems[J].Applied Ocean Research,2016(59): 254-264.

[8] KLINGAN K E.Automated optimization and design of mooring systems for deep water[D].Norwegian University of Science and Technology,2016.

[9] 余龙,谭家华.深水多成分悬链线锚泊系统优化设计及应用研究[J].华东船舶工业学院学报(自然科学版),2004,18(5):8-13.(YU Long,TAN Jiahua.Research and application of optimum design of deepwater multi-component mooring line [J].Journal of East China Shipbuilding Institute (Natural Science Edition),2004,18(5):8-13.(in Chinese))

[10] 余龙,谭家华.基于准静定方法的多成分锚泊线优化[J].海洋工程,2005,23(1): 169-173.(YU Long,TAN Jiahua.Research on optimum multi-component mooring lines based on catenary equation [J].The Ocean Engineering,2005,23(1): 169-173.(in Chinese))

[11] 周洋.深水悬链线锚泊系统多成分锚泊线设计[D].哈尔滨：哈尔滨工程大学.2008.(ZHOU Yang.Design of deepwater multi-component mooring line [D].Harbin: Harbin Engineering University.2008 (in Chinese))

[12] 樊磊,孙丽萍,王宏伟,等.半潜式起重平台系泊系统设计与优化研究[J].海洋工程,2015,33 (01): 31-38.(FAN Lei,SUN Liping,WANG Hongwei,et al.Investigation on mooring system design and optimization of a semi-submersible crane vessel [J].The Ocean Engineering,2015,33 (01): 31-38.(in Chinese))

[13] 李亚男,唐文献,张建,等.基于锚泊系统的半潜式海洋平台系泊缆长度优化方法研究[J].船舶工程,2014,03:115-118.(LI Yanan,TANG Wenxian,ZHANG Jian,et al.Research of optimizing mooring line length methods of semi-submersible platform based on mooring system [J].Ship Engineering,2014,03:115-118.(in Chinese))

[14] 王宽.基于BP神经网络仿真的系泊优化设计[D].天津大学,2012.(WANG Kuan.Optimum design of mooring system based on BP neural network [D].Tianjin University,2012.(in Chinese))

[15] 石建峰,陈红卫,王莉.半潜式钻井平台锚泊定位锚链张力优化[J].计算机测量与控制,2016,07:183-186.(SHI Jianfeng,CHEN Hongwei,WANG Li.Research on optimization of chain tension for mooring anchor for semi-submersible platform[J].Computer Measurement and Control,2016,07:183-186.(in Chinese))

[16] 张浩，陈国明，郑纯亮，等.内波参数对半潜式钻井平台漂移量的影响[J].石油钻采工艺，2015，37(1)：39-42.(ZHANG Hao,CHEN Guoming,ZHENG Chunliang,et al.Effect of internal wave parameters on drifting quantity of semi-submersible drilling platform [J].Oil Drilling & Production Technology,2015,37(1): 39-42.(in Chinese))

[17] 吴卫兵，尹建川.准确判断船舶走锚方法[J].中国航海，2012，35(4)：124-127.(WU Weibing,YIN Jianchuan.A method to find dragging anchor [J].Navigation of China,2012，35(4)：124-127 (in Chinese))

[18] 杨林家，杨佐昌，于洋.船舶走锚预警系统[J].大连海事大学学报，2005，31(1)：29-32.(YANG Jialin,YANG Zuochang,YU Yang.Vessel anchor dragging early warning system [J].Journal of Dalian Maritime University,2005,31(1)：29-32 (in Chinese))

[19] NEUBECKER S R,RANDOLPH M E.The static equilibrium of drag anchor in sand[J].Canadian Geotechnical Journal,1996,(33): 584-594.

[20] API RECOMMENDED PRACTICE 2SK.Recommended practice for design and analysis of stationkeeping systems for floating structures[S].Washington: Institute A P,1997.

[21] 孙佳君.海洋系泊链钢磨蚀损伤规律研究[D].大连理工大学，2014.(SUN Jiajun.The research of corrosive wear damage of marine engineering chain link [D].Dalian University of Technology,2014.(in Chinese))

[22] 刘金沅.锚链腐蚀磨损累积损伤评估方法研究[D].大连理工大学，2013.(LIU Jinruan.Research on approach for corrosion and wear cumulative damage assessment of chain links [D].Dalian University of Technology,2013.(in Chinese))

[23] 毛振东.系泊链钢的摩擦磨损与性能研究[D].江苏科技大学，2011.(MAO Zhendong.Research on friction wear and property resistance of mooring chain steel [D].Jiangsu University of Science and Technology,2011.(in Chinese))

[24] 荣雷，崔建辉，王永州.走锚全损事故及走锚后的应急预案分析[J].航海工程，2012，41(5):138-144.(RONG Lei,CUI Jianhui,WANG Yongzhou.Cause analysis of the dragging anchor casualty and the contingency plan [J].Ship & Ocean Engineering,2012，41(5):138-144.(in Chinese))

[25] 刘涛.浅谈船舶的走锚事故[C]//中国航海科技优秀论文集(2010).北京：人民交通出版社，2010：19-31.(LIU Tao.On the anchor dragging of ship[C]//China Academic Journal of Marine Science and Technology (2010).Beijing: China Communication Press,2010：19-31.(in Chinese))

Optimum design for composite mooring system components of semi-submersible drilling platform

LUO Ning1,ZHANG Hao1,2,SONG Qiang1,2,CHEN Guoming1,LIU Zhengli3,SHENG Jiliang1

(1.China University of Petroleum Centre for Offshore Engineering and Safety Technology,Qingdao 266580,China; 2.China Ship Scientific Research Center,Wuxi 214082,China; 3.Shenzhen Branch of CNOOC,Shenzhen 518067,China)

An optimum design method for composite mooring system components of semi-submersible drilling platform is proposed to decrease the chain length in mooring system in order to increase deploying and retracting efficiency of mooring line.Optimum design criterion and process are developed,combined with design parameters of mooring system.Hydrodynamic model of moored semi-submersible platform is established,and results of platform and mooring system are obtained based on ANSYS-AQWA.The optimum length of chain is 395m,by analyzing dimensionless parameters for offset of platform,minimum safety factor of mooring system,anchor dragging,grounding length of mooring line and uplift force of anchor,and considering the effect of pretension angle and pretension on steel chain reduction.The efficiency of deploying and retracting of mooring line is improved,and the variable load of platform is decreased.

composite mooring system; optimization design; semi-submersible platform

TE52

10.16483/j.issn.1005-9865.2017.05.011

1005-9865(2017)05-0095-08

2016-10-17

国家自然科学基金资助项目(51239008)；国家重点基础研究发展计划(“973”计划)资助项目(2015CB251203)；中海油深海开发有限公司资助项目(YXKY-ZY-2014-SHENHAI-03)

罗宁(1992-),男，湖南长沙人，硕士研究生，从事深水钻井技术与装备及锚泊安全方面的研究工作。E-mail:woshiluoning@vip.qq.com

陈国明。E-mail: offshore@126.com