基于PSO-DE算法的突发水域污染溯源研究

曹宏桂,贠卫国



基于PSO-DE算法的突发水域污染溯源研究

曹宏桂,贠卫国*

(西安建筑科技大学信息与控制工程学院,陕西西安710055)

利用PSO-DE混合优化算法结合移动监测平台研究了污染物源项识别问题,包括单点固定源和多点固定源位置的反演.该方法把源项识别反问题转化为非线性优化问题,用个移动平台检测并记录所在水域的污染物浓度,将各自位置的坐标值记为此移动平台的best,每一个移动平台均对应一个best,即共有个best,将个移动平台获取的污染物浓度值进行对比,选择最大污染物浓度值对应的水域坐标,记为best,以此作为初始种群先进行PSO优化获得的种群,再进行DE优化,取两者浓度高的作为best,直到获得浓度值最高的点,即污染物初始投放点.多个算例的计算结果表明,采用该算法对含点源的二维水域污染源溯源问题能够得到精度较高的反演结果.

PSO-DE；污染物溯源；移动监测平台；二维水域

污染物源项识别反问题是指根据环境水力学测量数据,来反推污染源信息的问题,如获取点源的个数、强度和位置等[1],是环境水力学反问题中一类重要的反问题,具有重要的研究价值和应用背景.目前相关方面的研究很多但尚不成熟,根据研究方法的特点,可以分为三类[2-3],第一类方法将污染源项识别问题转化为概率计算问题,利用概率和数理统计理论估算污染源的源项信息[4-5],如陈媛华等[4]使用相关系数法进行污染物源项信息识别,王家彪等[5]使用耦合概率密度溯源河渠突发水污染,朱嵩等[6]基于贝叶斯推理实现标准k-e湍流模型的参数识别,杨海东等[7]在微分进化和蒙特卡罗的基础上利用贝叶斯算法改进,提高其模型的稳定性和可靠性.但这类方法对于模型的准确性有非常高的要求,而由于环境水力模型在建模时有很多条件都是理想化的,所以最终的计算精度误差较大.鉴于这种情况,第二类方法采用对模型准确性不高的智能寻优算法,如辛小康等[8]采用遗传算法对水污染事故的源项信息进行识别,但是这种方法需要有足够的训练样本对模型进行训练,对于突发水域污染的情况无法获得足够数量的样本,所以可行性不高.第三类方法借鉴地下水污染的方法,将污染源溯源问题转化为寻找有限元的最优解问题[9-11],使用DE差分进化算法和PSO粒子群算法进行全局最优解的寻找.如牟行洋等[10], Jong等[12], Ednah等[13]都有类似的研究,但由于算法本身的特点,粒子群算法拥有较好的全局搜索能力,差分进化算法具有较强的局部搜索能力,如果可以将两个算法的优点结合将会获得更精确的寻优结果[12-15].

本研究采用有限元法作为含点源的二维环境水力学模型正演问题的数值计算方法,采用PSO-DE粒子群与差进化混合优化算法结合小型移动监测平台进行相应的参数反演研究,包括单点固定源反演和多点固定源反演.

1 数学模型

1.1 二维水域的单点稳态源污染物水质模型

模型为无限边际水体假设下的二维(水域纵向和横向)稳态点源排放的水质模型,假设当污染物投入水中时,在深度方向迅速扩散均衡.由于污染物是稳态点源污染物,既以恒定速率往水中注入污染物,当某水域出现污染物后,该水域中污染物的质量总量并不随着时间而改变,只和与污染源的相对坐标有关,与时间无关.

二维水域的单点稳态源(恒定速率排放污染物)污染物(惰性污染物)浓度的解析解如式1所示[16].

1.2 二维无限水域多点稳态源污染物水质模型

在二维的单点源污染模型的基础上,为了能够更加贴近实际的水域情境,将单点源污染物增至多点源污染物,在式1的基础上,推导出此时二维多点稳态源(恒定速率排放污染物)污染物水域的污染物浓度解析解为:

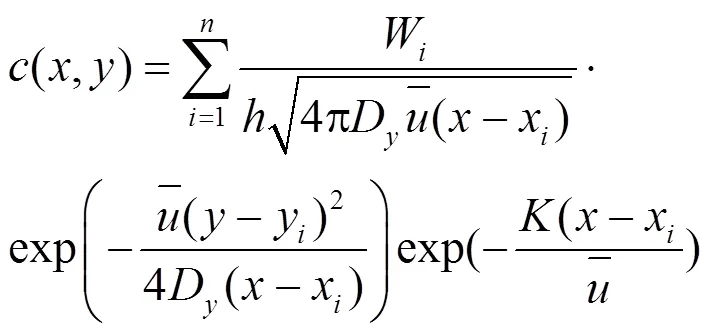
同样的,由于此时仍旧为稳态源排放污染物,因此水域中污染物的质量总量为恒定值,与时间无关.式2可以用来模拟大型二维水域同时存在多个同类点源污染物稳定排污情景下的水域各个断面的污染物浓度.

2 PSO-DE粒子群与差进化混合优化算法

粒子群算法是由Keimedyl和Eberhart 1995年提出,源于对鸟群捕食行为的研究.用于解决优化问题.粒子群进化算法虽然收敛速度较快、容易实现,在各种问题的求解和应用已经展现其独特的优点,但在收敛过程中容易停滞,收敛精度较低.微分进化算法作为一种新的算法,近年来才引起广大学者的关注,算法具有易于操作,优化性能好等特点,但容易陷入局部最优,特别是到了进化后期收敛速度明显降低[17-18].

为了改善粒子群进化算法和微分进化算法独自求解优化问题的不足.本文引用文献中的粒子群算法和微分进化算法混合的方法.该算法是对种群先后做PSO和DE优化的策略,对于一个种群,先通过PSO优化找到最优解得大概位置,再运用DE优化找到最优解,为了协调全局和局部搜索能力,新算法采取惯性权重和学习因子非线性变化策略;而为了提高算法跳出局部最优的能力,在DE优化时采取放缩因子非线性变化策略.

PSO-DE算法的具体实现框架如下:

步骤1:粒子群初始化.初始速度和位置,将每个小型移动平台的初始坐标赋值为种群的初始值,种群规模NP即为平台个数,最大迭代次数itermax,惯性权重最大值max,惯性权重最小值min,学习因子1、2,变异概率CR,每个粒子的适应度最好的点best被设置为其初始位置,best中的适应度最好的点被设置成为全局最佳粒子best.

(1)惯性权重因子

惯性权重是影响算法性能的关键参数,根据其特点,在粒子群迭代的初期因具有较好的全局搜索能力,到达后期,则更希望粒子具有较好的局部搜索能力[19].提出了以下动态变化的惯性权重:

式中:iter和itermax分别是当前迭代次数和最大迭代次数,max和min分别为惯性权重的初始最大值和最小值,一般取max=0.9,min=0.4.

(2)时变学习因子

在粒子群进化算法中,学习因子1和2分别影响着每个粒子的个体最优和全局最优.较小的学习因子会限制粒子的运动,而较大的学习因子会使粒子过于发散.基于此提出了时变学习因子策略:

式中:11、12、21和22是常数,iter和itermax分别是当前及最大迭代次数.当11=21=1.5时,12=22=0.5算法的优化性能最好.

步骤 2: PSO优化阶段.

(1):通过下列公式修正速度与位置:

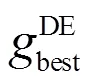
步骤5:如果满足结束条件,即达到最大迭代次数,则循环结束输出结果,否则跳转回步骤2.

3 数值算例

3.1 单点源算例分析

3.1.1 算例来源 假设某个大型的湖泊,在位置A排放2000kg惰性污染物,该湖泊的平均水深为l0m,平均水流速度0.5m/s,横向弥散系数50m2/ min[20].该水域相关断面的污染物浓度可以通过公式(1)来计算.令位置A为坐标原点(0,0),选取水域纵向100m(步长为0.5)横向200m(步长为1)的范围绘制污染物浓度分布如图1所示.

图1 二维水域单点稳态源污染物浓度分布

图2 单点源最佳粒子运动轨迹

表1 单点源算例的最佳粒子坐标值

3.2 多点源算例分析

3.2.1 算例来源 假设污染源在单点固定源算例的基础上增加到3个点源,即=3.3个点源的位置分别为(0m,0m)、(50m,-50m)和(60m,60m),3个点源的污染物质量分别为2000,1000和300kg.其他条件保持不变.其浓度分布图如图3所示.

3.2.2 结果分析 对于多点源的情况,依然搜索全局范围内污染物浓度最大的点,即坐标值为(0,0)的点.最佳粒子的运动轨迹如图4所示.其坐标值如表2所示.

图3 二维水域多点稳态源污染物浓度分布

图4 多点源最佳粒子运动轨迹

表2 多点源算例的最佳粒子坐标值

通过图4可以看出,多点源情况下在开始搜索的时候出现了往复,但最终收敛在污染物浓度最大点.通过表2数据显示,在迭代到第40次时达到污染物最大的点附近并保持稳定.所以PSO- DE优化算法在多点源情况下依然可以达到要求.对于另外的2个污染源暂时不能准确获取其坐标,但是其大致范围基本可以确定在粒子出现多次往复的区域.

3.3 反演结果影响因子分析

3.3.1 粒子个数的影响 实际应用过程中初始种群的粒子数关系到成本问题,因此考察单点源反演过程中不同的粒子数对反演结果的影响.

由表3可知,在粒子数不同的情况下,本算例中随着粒子数的增加,其反演结果的精度也随之提高,但是考虑到实际应用中成本问题,结合反演结果的误差,建议实际应用时粒子数设置为5.

表3 粒子个数对反演结果的影响

表4 水流速对反演结果的影响 Table 4 Influence of inversion results for water velocity

由表4可知,在其他情况相同的情况下,水流的流速越快对反演计算的影响越大,溯源精度越低.在流速较快的水域可以通过增加粒子数量来提高反演精度,或者增加迭代次数来解决.

4 结论

本研究考虑了污染物水质特征,给出二维水域下适用于移动平台的PSO-DE优化溯源算法.对PSO-DE算法中的惯性权重因子和时变学习因子进行改进,通过MATLAB进行算例仿真,在单点源污染的情况下,污染源定位坐标值为(0.001818,0.3972),与实际位置误差仅为0.3972m;多点源污染的情况下,确定了排放量最大的点坐标，同时确定了其他污染源的范围.结果表明本方法的计算结果接近真实情况.探讨和分析论证了所提出的算法在实际运用时可能遇到的问题,具有一定的应用价值.

[1] 朱 剑,杨 江,邓尚超.适用于移动平的河流突发污染算法研究 [J]. 安全与环境学报, 2015,15(6):295-299.

[2] Gurhan G, Halil K. Solving inverse problems of groundwater- pollution-source identification using a differential evolution algorithm [J]. Hydrogeology Journal, 2015,23:1109–1119.

[3] Jyoti C, Deepak K. Groundwater pollution source identification through inverse modeling [J]. Water Resources and River Engineering, 2015.

[4] 陈媛华,王 鹏,姜继平,等.基于相关系数优化法的河流突发污染源项识别 [J]. 中国环境科学, 2011,31(11):1802-1807.

[5] 王家彪,雷晓辉,廖卫红,等.基于耦合概率密度方法的河渠突发水污染溯源 [J]. 水利学报, 2015,46(11):1280-1289.

[6] 朱 嵩,刘国华,毛欣炜,等.基于贝叶斯推理的标准k-ε湍流模型参数识别 [J]. 四川大学学报(工程科学版), 2010,42(4):78- 82.

[7] 杨海东,肖 宜,王卓民,等.突发性水污染事件溯源方法[J]. 水科学进展, 2014,25(1):122-129.

[8] 辛小康,韩小波,李 建,等.基于遗传算法的水污染事故污染源识别模型 [J]. 水电能源科学, 2014,(7):52-55.

[9] 叶永伟,葛沈浩,任设东,等.基于PSO-DE算法的污水处理优化控制研究[J]. 计算机测量与控制, 2016,24(2):68-76.

[10] 牟行洋.基于微分进化算法的污染物源项识别反问题研究术 [J]. 水动力学研究与进展, 2011,26(1):24-30.

[11] 彭 亮,于 晖.基于浓度梯度-逆流搜索的污染源定位策略 [J]. 智能计算机与应用, 2012,2(6):64-66.

[12] Jong C, Meng G W, et al. Structural reliability-based optimization design using PSO-DE hybrid algorithm [J]. Journal of South China University of Technology, 2014,42(9): 41-45.

[13] Ednah O, Akpofure T, John N. Groundwater pollution source identification by optimization and the green element method [J]. World Environmental and Water Resources Congress, 2016, 309-318.

[14] MT A. A hybrid simulation–optimization approach for solving the areal groundwater pollution source identification problems [J]. Journal of Hydrology, 2016,538:161–176.

[15] 肖传宁,卢文喜,赵 莹,等.基于径向基函数模型的优化方法在地下水污染源识别中的应用 [J]. 中国环境科学, 2016,36(7): 2067-2072.

[16] 傅国伟.河流水质数学模型及其模拟计算[M]. 北京:中国环境科学出版社, 1987.

[17] Yu F Y, Chen X, Guo L. Hybrid algorithm based on particle swarm optimization and differential evolution [M]. Journal of computational information system, 2012.

[18] Singh R M, Datta B. Identification of groundwater pollution sources using GA-based linked simulation optimization model [J]. Journal of Hydrologic Engineering, 2006,11(2):1216-1227.

[19] 高岳林,刘军民.差分进化算法的参数研究 [J]. 黑龙江大学自然科学学报, 2009,26(1):81-85.

[20] 郑 彤.环境系统数学模型[M]. 北京:化学工业出版社, 2003.

Research of the abrupt waters pollution source based on optimization algorithm of PSO-DE.

CAO Hong-gui, YUN Wei-guo*

(School of Information and Control Engineering, Xi'an University of Architecture and Technology, Xi’an 710055, China)., 2017,37(10)：3807~3812

The optimization algorithm of PSO-DE cooperated with mobile monitoring platform was studied to solve the inverse problem of pollution, which included inversion of the position of the single point and multiple-point stationary sources. The inverse problem of pollution source was transformed into nonlinear optimization problem. The pollutant concentration of waters were detected and recorded bymobile platforms; the coordinate of mobile platform was denoted bybest, and they were corresponded one by one, there would be Nbestaltogether. The pollutant concentration of waters which attained by the mobile platform would be compared with each other, and the coordinate of maximum pollutant concentration would be chosen and marked asbest. First, thebestwould be the initial population for the PSO optimization. Second, the population would be used for DE optimization. Finally, thebestwould be chosen from the high concentration of both until the highest point of pollutant concentration was obtained, which was the initial point of pollutant. The calculation results of examples showed that the algorithm could attained a high precision inversion results for pollutant source traceability problem of two-dimensional waters.

PSO-DE；pollutant source traceability；mobile monitoring platform；two-dimensional waters

X52

A

1000-6923(2017)10-3807-06

曹宏桂(1991-),男,陕西榆林人,西安建筑科技大学硕士研究生,主要研究领域为嵌入式开发,智能控制.发表论文2篇.

2017-03-14

住房和城乡建设部科学项目计划(2016-R2-045)

* 责任作者, 教授, yun_weiguo@aliyun.com