基于模糊事故树的边坡预应力锚索可靠性分析

陈沅江，洪 涛

(中南大学资源与安全工程学院，湖南 长沙 410083)

基于模糊事故树的边坡预应力锚索可靠性分析

陈沅江，洪 涛

(中南大学资源与安全工程学院，湖南 长沙 410083)

通过已有软岩边坡锚索监测资料，结合锚索预应力损失影响因素以及损失机理，构建边坡锚索预应力损失事故树。引入了模糊集理论，采用3σ法则和改进模糊语言将基本事件的不确定概率转化为梯形模糊数，应用模糊算子计算出事故树中顶事件发生的模糊概率，进行了模糊重要度分析，明确了系统的薄弱环节，并提出了降低该边坡锚索预应力损失的合理措施。分析结果表明，模糊事故树法能将主观判断做出客观描述，并科学有效的评价边坡锚索锚固可靠性问题，为边坡锚固工程失效事故的安全预警提供了新思路。

模糊事故树；锚索预应力损失；梯形模糊数；可靠性分析；预应力锚固失效

预应力锚索广泛应用于边坡支护工程中，它具有主动加固、深层加固、布置灵活、施工快速、经济性好等显著特点。但在长期使用过程中，边坡锚索受外部环境和施工工艺的制约，锚索的预应力值往往损失很大，使得有效预应力值低于临界安全值，边坡失稳的情况屡有发生，造成人身伤亡和经济损失。考虑到国内外边坡锚固工程数量较多，且使用时间长，因此开展边坡预应力锚索的可靠性分析至关重要。

张永安等[1]通过凤凰谷水电站泥质岩边坡的预应力锚索系统监测资料分析，探讨泥岩高边坡锚索预应力的锁定损失，短、长期变化规律及降雨、补偿、张拉对预应力的影响。这类分析的准确性取决于监测设备的精确性，且忽略影响因素之间的相关性，缺乏对系统结构、作用机理的认识。李英勇等[2]将影响锚索预应力变化的因素归结为可补救、长期作用和周期波动三类，并依托经验公式和构建组合模型定性定量分析锚固工程长期稳定性。然而边坡预应力锚索系统具有一定的模糊性，理论公式的准确有待商榷，边坡锚索可靠性难以准确反应。

近年来，不确定性理论逐渐应用在岩土安全领域，阮波等[3]运用灰色关联度分析方法，分析了锚索的锁定荷载、自由段长度及锚固段长度对预应力锚索锁定损失的影响；何书等[4]采用三角形直觉模糊数概念，构建了评价指标的隶属度和非隶属度函数，并基于 TOPSIS 决策方法建立了赣南稀土矿区滑坡稳定性分级评价模型；刘光华等[5]通过宏观分析缓倾顺向边坡由失稳至破坏的各阶段特征，提出了其稳定性状态的影响因素,运用模糊数学理论和方法确定每个因素的权重值,对其进行稳定性判别。模糊事故树(MFTA)是一种将事故树与模糊集理论[5]结合，定义模糊事件的隶属函数来表示其发生程度，对模糊系统进行系统安全分析的方法。本文依托湖南西部某高速公路的K123典型风化软岩边坡锚索预应力监测资料，运用模糊事故树法合理处理边坡锚索系统中基本事件失效概率的随机不确定性，量化评估基本事件的敏感度，以期准确地找出风化软岩边坡锚固系统中相对薄弱的环节，为工程管理人员的合理决策提供理论依据。

1 边坡锚固工程概况

湖南西部某高速公路的K123风化软岩边坡，边坡坡高76 m，走向长209 m，自然坡比1∶1.16。边坡岩层以风化泥质页岩为主，岩石强度较低，遇水易破裂，为典型的风化岩边坡[6]。边坡总体为单斜构造，构造类型简单，未见其他不良地质构造迹象，岩层层面与坡面反向，该地段地震动峰值加速度为0.05g，地震动反应谱特征周期为0.35 s，无需考虑地震的影响。由于边坡的稳定安全系数计算结果为0.75～1.06，属于不稳定边坡，因此采用锚索-地梁进行联合支护。锚固边坡采用拉压分散型锚索，索体由4根高强度低松弛无粘结钢绞线组成，张拉载荷为600 kN。采用新边法进行边坡锚固，锚索施工程序规范，未出现锚索断裂破坏的情况，锚索间距5 m，灌浆材料选用水泥砂浆材料，养护后强度大于30 MPa。

2 K123边坡锚索预应力影响因素分析

在边坡支护工程中，锚索的预应力衰减直接影响到支护效果。工程实践[6-9]表明，影响锚索预应力变化的因素很多，主要包括外界环境因素和内部自身因素。外界环境因素对锚索预应力损失的影响源于自然界的客观条件，环境改变如边坡地质条件、气候变化等。这类因素的影响是难以通过主观行动消减。内部自身因素对锚索预应力损失的影响源于施工设计缺陷、工程管理的不到位，主要包括锚固系统和边坡施工两个方面，这类因素造成的影响可以通过改进施工工艺，加强现场工程管理予以控制。按照不同因素影响锚索预应力变化的时程长短，将预应力变化规律分为时效性变化规律、瞬时变化规律、波动变化规律。通过对这些因素的影响方式、作用机理、应力变化规律的分析研究，有利于对现场锚索预应力监测结果的恰当评价，预防工程地质灾害的发生。根据K123边坡的实际工程概况，分析得锚索预应力损失影响因素见表1。

表1 边坡锚索预应力损失影响因素Table 1 Anchor cable prestress loss factors

3 K123边坡锚索预应力损失的模糊事故树分析

3.1事故树建立

事故树分析是一种图形演绎法，是事故在一定条件下的逻辑推理方法，能将导致系统事故的各种可能因素用逻辑“与”、“或”关系连接起来形成倒立的树状图，从而有利于找出系统的薄弱环节。编制事故树起点的关键是要确定顶事件，针对分析对象的特点，把对系统影响大的灾害或事故做为分析研究的对象。以K123边坡锚索预应力损失做为顶事件，不考虑锚固系统突发破坏和预应力激增的情况，结合表1分析得到的边坡锚索预应力损失影响因素，编制了K123风化岩边坡锚索预应力损失事故树见图1。由图1可见，该事故树包含8个中间事件，17个基本事件，不同事故树层次的事件通过逻辑“与”和“或”门连接。边坡锚索预应力损失(T)主要是由于锚固系统自身引起的预应力损失(M1)、外部环境引起的预应力损失(M2)、边坡施工引起的预应力损失(M3)导致的，为逻辑或门关系，此为事故树第一层；在第二层中，材料引起的预应力损失(M4)和锚索施工引起的预应力损失(M5)是锚固系统引起的预应力损失(M1)的必要条件，它们与M1为逻辑与门关系；外部环境引起的预应力损失(M2)发生的主要原因是边坡岩体(M6)、水(M7)、大气温度(X12)、地震力(X13)，为逻辑或门关系；边坡卸荷(X14)、爆破荷载(X15)、机械振动(X16)、群锚效应(X17)是引起边坡施工的预应力损失的原因，为或门关系；在第三层中，灌浆材料徐变(X1)或钢绞线松弛(X2)是材料引起的预应力损失(M4)的主要原因，为或门关系。锚索施工引起的预应力损失(M5)主要是源于孔斜率摩擦损失(X3)，封孔灌浆损失(X4)以及锁定损失(M8)，为逻辑或门关系。边坡岩体(M6)导致预应力损失是围岩蠕变(X8)和围岩弹塑性形变(X9)的同时作用的结果，为逻辑与门关系。地下水(X10)和降雨(X11)是水(M7)导致锚索预应力损失的主要原因，为逻辑或门关系；第四层是锚索的锁定损失(M8)，主要是由于锚具夹片回弹(X5)、张拉系统摩擦阻力(X6)、锚墩瞬时形变(X7)引起的，为逻辑或门关系。

图1 K123风化岩边坡锚索预应力损失事故树图

3.2边坡锚索预应力损失事故树定性分析

事故树定性分析的主要目的是求取最小割(径)集，通过最小割集来发现导致系统失效或顶事件发生的全部可能原因，并定性地识别系统的薄弱环节，以确定顶上事件不发生的几种可能方案，为控制事故发生提供依据。常用的求解最小割集方法是布尔代数法和行列式法，本文利用布尔代数法对K123锚固边坡事故树自上而下进行简化，求解边坡锚索预应力损失事故树布尔代数表达式如下：

T=M1+M2+M3=M4M5+M6+M7+X12+X13+X14+

X15+X16+X17=(X1+X2)(X3+X4+X5+X6+X7)+

X8X9+X10+X11+X12+X13+X14+X15+X16+X17

通过分解上式即可求得最小割集见表2。

表2 K123风化岩边坡锚索预应力损失事故树最小割集Table 2 The minimum cut sets of slope anchor cableprestress loss fault tree

由表2可知，K123风化软岩边坡锚索预应力损失事故树的割集数量有19个，代表19种可能的锚索预应力失效的事故模式。以割集C14为例，该割集的含义是因灌浆材料徐变、封孔灌浆二者同时导致的预应力损失超过临界值时，就会构成锚固失效事故发生的充分条件。因此，凭借事故树的定性分析确定的所有事故链，掌握该边坡锚固失效发生的所有可能情况，可以为锚固工程的安全管理提供正确的引导，提升对边坡锚固系统所处风险状态的警惕。

3.3锚索预应力损失事故树定量分析

事故树定量分析中最重要的是要确定事故树中各基本事件的发生概率。但考虑到边坡锚固工程领域尚未建立可靠的行业失效数据库，底事件尚无精确的概率统计，因此本文引用模糊集理论来处理边坡锚固系统中的随机不确定概率信息，通过将基本事件的不确定概率用模糊概率来代替，以减少事故树定量分析中因主观判断产生的误差。

(1)

式中：a和d——称为梯形模糊数的下限和上限，称为相对最可能值区间。

图2 梯形模糊数

3.3.1有统计概率的基本事件概率模糊化

笔者根据工程类比的思想，统计分析了近年来一些软岩边坡锚固监测资料以及国内外关于锚索失效概率研究成果，总结出一些基本事件的经验概率值，但由于不同工程之间的特殊性，一些基本事件的发生概率在一定范围内随机波动。因此立足于K123边坡锚固工程概况，采用一个3人的专家小组打分评判基本事件的发生概率，并取打分概率的均值为m，标准差为σ，运用3σ法则[11]对分值进行梯形模糊数转化，模糊数表征为(3σ,m,m,3σ)。该方法确定的基本事件有6个，分别是钢绞线松弛(X2)、孔斜率摩擦损失(X3)、封孔灌浆损失(X4)、锚具夹片回弹(X5)、张拉系统摩擦损失(X6)、围岩蠕变(X8)，其梯形模糊数见表3。

3.3.2无统计概率的基本事件概率模糊化

在边坡锚固工程中，由于系统元素涉及范围广，基本事件难以获得足够的统计数据来计算准确的基本事件发生概率。为解决这一问题，通过一个3人的专家小组根据专家经验先用模糊语言评估事故树中各事件的发生频率，然后将模糊性语言转化为模糊数形式。目前常用的标准转化的模糊语言值集合[12]为{很小、小、较小、中等、较大、大、很大}。由于国内现有模糊语言转换途径存在概率数量级偏大的情况，不贴近工程实际，因而本文参考美国杜邦公司的“故障概率语言评价标准”[13]，提出一种新的转换标准，更加贴近工程安全评价中的实际情况，新的转换标准见图3。模糊语言集确定的基本事件有11个，分别为X1、X7、X9、X10、X11、X12、X13、X14、X15、X16、X17，其梯形模糊数见表3。

表3 有统计概率的基本事件的模糊概率Table 3 Fuzzy probability of basic events having statistical probability

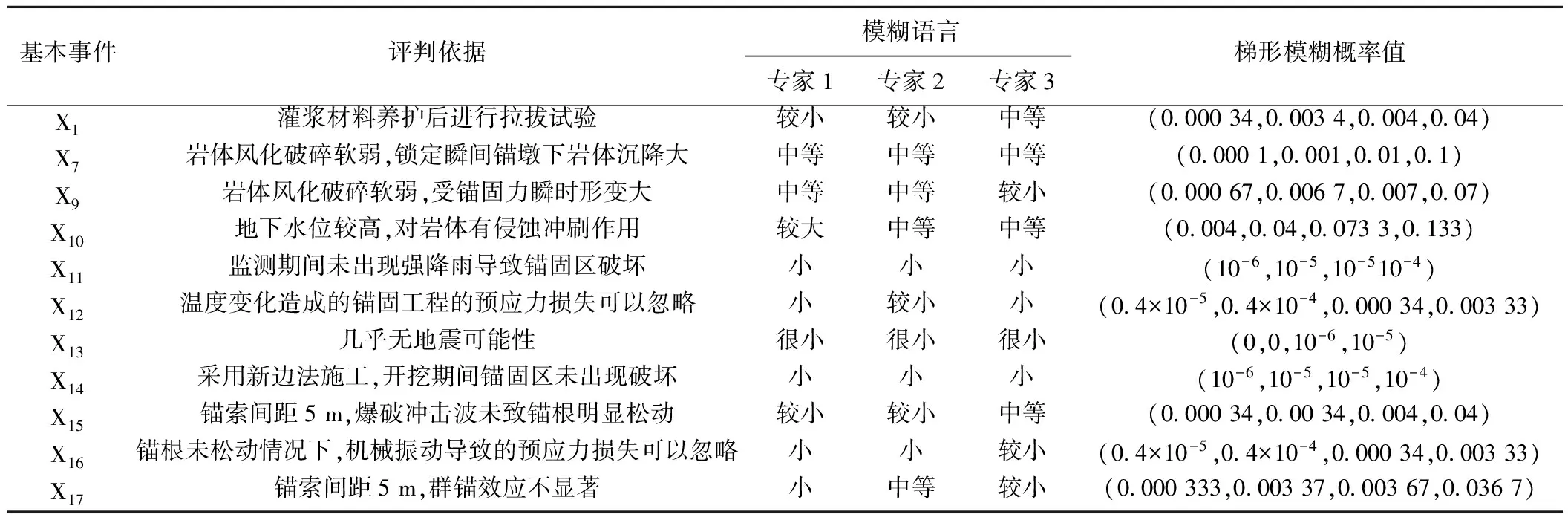
表4 无统计概率的基本事件的模糊概率Table 4 Fuzzy probability of basic events that have no statistical probability

图3 改进模糊语言转换途径

由边坡锚索事故树定性分析所求解的顶事件布尔代数表达式，运用逻辑门算子求解顶事件发生的模糊概率，计算得到顶事件发生的模糊概率qt=(0.005 3,0.054 7,0.091,0.228)，即K123风化软岩边坡锚索预应力损失失效的概率在5.47%～9.1%之间的可能性最大，其隶属度为1。对顶事件模糊概率进行解模糊化处理，采用中心面积法[14]可得到顶事件发生的清晰概率值为0.099 9。

3.4模糊重要度分析

模糊重要度反映基本事件对顶事件发生的影响重要程度，基本事件的模糊重要度越大，表示其对系统的影响越大。因此要提高系统的可靠性，改善系统的薄弱环节，应首先考虑如何处理模糊重要度大的事件。对于边坡锚固系统，基本事件的故障数据的可能性函数皆为正有界闭模糊数，因此选用计算简便，易于理解的中值法进行模糊重要度分析。

设边坡预应力锚索损失事故树的结构函数为f(x1,x2…x17)，记顶事件、基本事件的中位数分别为Td、Ti，任一基本事件的模糊重要度Si。根据模糊重要度的定义Si=Td-Ti，因为计算任意事件的模糊重要度时，顶事件的中位数Td一致，所以比较各基本事件模糊重要度大小时只需比较基本事件的中位数Ti大小。考虑到求解梯形模糊数的中位数计算复杂，一般先把梯形模糊数转化为三角模糊数，再计算三角模糊数的中位数，具体转化方式模糊数(3σ,m,3σ)；对于采用模糊集语言确定的梯形模糊数，先根据式(2)求出梯形模糊数(a,b,c,d)的重心m，再根据文献[15]中的方法，由转化三角模糊数(l,m,u)中的l,m,u关系式(3)予以确定。

(2)

m-l=u-m=0.055 6m

(3)

待边坡锚索预应力的所有基本事件的梯形模糊数转化成三角模糊数后，根据公式(4)[16]求解三角模糊数(l,m,u)的中位数，得到边坡锚索预应力失效事故树的基本事件的模糊重要度见表5。

(4)

表5 边坡锚索预应力损失各基本事件中位数Table 5 The median of slope anchor cable prestressloss basic events

对表5中位数大小进行排序，得到模糊重要度最大的5个基本事件依次为：围岩蠕变(X8)、地下水位(X10)、锚具夹片回弹(X5)、孔斜率摩擦损失(X3)、锚墩瞬时弹塑性形变(X7)。这5个基本事件是导致风化岩边坡锚固系统失效的薄弱环节，工程安全管理人员应该针对薄弱环节制定合理有效的安全措施。基本事件X3、X5属于因施工人员操作技能、锚具的自身缺陷造成的预应力瞬时损失，造成的风险可通过在锚索施工阶段使用高精度、高可靠性的钻孔设备，采用整索分级张拉程序，提高作业人员的操作技能等方法予以控制；基本事件X7、X8、X10属于因地质构造的特殊性造成的预应力损失，由于边坡岩体强度低且遇水易破裂，依靠改进锚索施工设计、人为操作改进的遏制效果有限。尤其对于软岩边坡，X8造成的预应力损失是具有时效性的，随着时间的增长，围岩蠕变造成的锚索预应力损失会愈加严重，因此相比其他导致预应力瞬时损失的因素引起的风险更大，对边坡锚固工程的危害性必须严格重视，工程后期需要加强对不良地质结构处的锚索预应力的实时监测，并适时对预应力损失较大的锚索进行补偿张拉。

4 结论

(1)建立了边坡锚索预应力损失模糊事故树模型，可以直观清晰地分析边坡锚索预应力损失直接、深层次的原因，同时解决了锚固边坡的基本事件发生概率不确定的问题。该方法简单易懂，不需要很多的原始数据，就能将现场实际情况与工程技术人员的经验充分结合起来，具有较高的应用价值。

(2)将模糊事故树应用于湖南某高速K123风化岩边坡锚索预应力可靠性分析过程中，全面阐述与演绎了顶事件与基本事件的逻辑关系。分析结果表明，围岩蠕变、锚具夹片回弹、地下水位、孔斜率摩擦损失、锚墩瞬时弹塑性形变是导致边坡锚索预应力损失失效的关键因素。因此，提高系统的安全度主要在于加大对锚索预应力损失时效性监测，并通过调整施工工艺，适时对预应力损失较大的锚索进行补偿张拉，避免锚固力低于安全阈值。

(3)鉴于各类岩土工程的基本事件发生概率缺乏精确概率统计且相关性不明确的问题，有必要建立和完善相关基本事件发生概率数据库，同时引入事故树计算机辅助软件构建适合于不同岩土工程可靠性分析的智能化系统。

[1] 张永安, 李峰, 蒋鸥. 泥岩高边坡锚索预应力变化规律分析[J]. 岩石力学与工程学报, 2007, 26(9): 1888-1892.

ZHANG Yongan, LI Feng, JIANG Ou. Analysis of prestress variation of cable in mudstone high slope reinforcement[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(9): 1888-1892.

[2] 李英勇, 王梦恕, 张顶立, 等. 锚索预应力变化影响因素及模型研究[J]. 岩石力学与工程学报,2008, 27(增1):3140-3146.

LI Yingyong, WANG Mengshu, ZHANG Dingli,et al. Study on influential factors and model for variation of anchor cable prestress [J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(s1):3140-3146.

[3] 阮波, 肖武权. 预应力锚索锁定损失影响因素的灰色关联度分析[J]. 铁道科学与工程学报, 2011,8(3):38-41.

RUAN Bo, XIAO Wuquan. Influence factors of load at lock off of prestressed anchors based on grey relevant degree theory[J]. Journal of Railway Science and Engneering, 2011,8(3):38-41.

[4] 何书, 陈飞. 基于直觉模糊集 TOPSIS 决策方法的滑坡稳定性评价[J]. 中国地质灾害与防治学报, 2016, 27(3):22-28.

HE Shu, CHEN Fei. Research of landslide stability assessment based on intuitionistic fuzzy sets TOPSIS multiple attribute decision making method [J]. The Chinese Journal of Geological Hazard and Control, 2016, 27(3):22-28.

[5] 刘光华, 张玲, 赵鹏, 等. 模糊数学在缓倾顺向边坡稳定性判别中的应用[J]. 中国地质灾害与防治学报, 2015, 26(2): 23-29.

LIU Guanghua, ZHANG Ling, ZHAO Peng, et al. Application of fuzzy mathematics in stability estimation of the rock slopes controlled by gently dipping joints[J]. The Chinese Journal of Geological Hazard and Control, 2015, 26(2) : 23-29.

[6] 陈沅江，尹进，胡毅夫. 软岩边坡锚索预应力定量损失规律研究[J]. 岩石力学与工程学报, 2013, 32(8):1685-1691.

CHEN Yuanjiang, YIN Jin, HU Yifu. Research on prestress quantitative loss law of soft rock slope anchor cable[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(8):1685-1691.

[7] 杨伦标, 高英仪.模糊数学原理及应用[M]. 广州:华南理工大学出版社,1992.

YANG Lunbiao, GAO Yingyi. Principle and application of fuzzy mathematics[M].Guangzhou：South China University of Technology Press,1992.

[8] 朱晗迓, 孙红月, 汪会帮, 等. 边坡加固锚索预应力变化规律分析[J]. 岩石力学与工程学报,2004,23(16): 2756-2760.

ZHU Hanya, SUN Hongyue, WANG Huibang,et al. Analysis on prestress state of cable applied to rock slope reinforcement[J]. Chinese Journal of Rock Mechanics and Engineering, 2004,23(16): 2756-2760.

[9] 汪剑辉, 张胜民, 赵强. 边坡加固中锚索预应力损失影响因素及对策探讨[J]. 施工技术,2007, 36(8): 25-27.

WANG Jianhui, ZHANG Shengmin, ZHAO Qiang. Discussion on influencing factors and countermeasures of loss of cable anchor’s prestress in reinforcing slopes engineering[J]. Construction Technology, 2007, 36(8): 25-27.

[10] 王清标, 王以功, 孙彦庆, 等. 不同岩性条件下预应力锚索锚固力损失规律研究[J]. 工程地质学报,2012, 20(5): 850-854.

WANG Qingbiao, WANG Yigong, SUN Yanqing, et al. Features of anchoring force loss in prestressed anchor cable under different lithologies[J]. Journal of Engineering Geology, 2012, 20(5): 850-854.

[11] 陆锡铭, 朱晗迓. 破碎岩质边坡中群锚效应试验研究[J]. 公路交通科技,2005,22(6):66-68.

LU Ximing, ZHU Hanya. Experiment and research on multi-anchorage effect in cracked rock slope[J]. Journal of Highway and Transportation Research and Development,2005,22(6):66-68.

[12] 李如忠, 童芳, 周爱佳, 等. 基于梯形模糊数的地表灰尘重金属污染健康风险评价模型[J]. 环境科学学报, 2011,31(8):1790-1798.

LI Ruzhong, TONG Fang, ZHOU Aijia, et al.Fuzzy assessment model for the health risk of heavy metals in urban dusts based on trapezoidal fuzzy numbers[J]. Acta Scientiae Circumstantiae,2011,31(8) : 1790-1798.

[13] 伍爱友, 施式亮, 王从陆. 基于事故树方法与三角模糊理论耦合的城市火灾风险分析[J]. 中国安全科学学报,2009,19(7):31-36.

WU Aiyou, SHI Shiliang, WANG Conglu. Urban fire risk analysis based on fault tree method and tri-fuzzy theory[J]. China Safety Science Journal, 2009,19(7):31-36.

[14] 卢雷, 肖文杰. 改进的模糊事故树分析方法[J]. 电光与控制,2010,17(11):93-96.

LU Lei,XIAO Wenjie. An improvedfuzzy fault tree analysis method[J]. Electronics Optics& Control, 2010,17(11):93-96.

[15] 段万寿, 刘琼, 艾云平. 基于模糊事故树的海岛阵地弹药储存失效分析[J]. 四川兵工学报,2008, 29(1):39-41.

DUAN Wanshou, LIU Qiong, AI Yunping. Island position ammunition storage failure analysis based on the fuzzy fault tree[J]. Journal of Sichuan Ordnance, 2008, 29(1):39-41.

[16] 王大庆, 张鹏, 郭龑,等. 考虑相关性时LNG储罐泄漏模糊事故树定量分析[J]. 中国安全科学学报,2014,24(1):96-102.

WANG Daqing, ZHANG Peng, GUO Yan, et al. Fuzzy fault tree quantitative analysis of LNG storage tank leakage with consideration of event interdependencies[J]. China Safety Science Journal,2014,24(1):96-102.

Reliabilityanalysisofslopeprestressedanchorcablebasedonthefuzzyfaulttree

CHEN Yuanjiang,HONG Tao

(SchoolofResourcesandSafetyEngineering,CentralSouthUniversity,Changsha,Hunan410083,China)

Through the cable monitoring data of weathered soft rock, combined the influencing factors and the damage mechanism of cable prestress loss , the slope anchor cable prestress loss fault tree was built. Fuzzy set theory was introduced. Then using 3σ law and improved fuzzy language turned the uncertain probability of basic events into trapezoidal fuzzy numbers .Fuzzy operators were applied to calculate the fuzzy probability of top event, then the fuzzy importance analysis was carried to clear the weak link of the system. Finally, reasonable measures to reduce slope anchor cable prestress loss were put forward. The analysis shows that the fuzzy fault tree method could make objective description to subjective judgment, and solve the slope anchor cable anchorage reliability problems effectively and accurately, providing a new way to the safety warning of slope anchor cable anchorage failure accidents.

fuzzy fault tree; cable prestress loss; trapezoidal fuzzy numbers; reliability analysis; prestress anchorage invalidation

X799.1

A

1003-8035(2017)03-0087-07

10.16031/j.cnki.issn.1003-8035.2017.03.13

2016-08-29;

2016-10-31

国家自然科学基金(51274251);交通部西部交通科技中心项目(20083187581)

陈沅江(1970-)，男，汉族，湖南湘潭人，博士，副教授，主要从事岩土与环境安全工程方面的研究工作。E-mail：cyjsafety@126.com

洪 涛(1990-)，男， 汉族，湖南邵阳人，硕士研究生，主要从事岩土安全工程方面的研究。E-mail：1138695062@qq.com