滑坡泥石流风险防御工程效益评估的最优值距模型
2017-11-07乔建平吴彩燕
乔建平,黄 栋,王 萌,吴彩燕
(1.中国科学院地表过程与山地灾害重点实验室, 四川 成都 610041; 2.中国科学院成都山地灾害与环境研究所, 四川 成都 610041;3.西南科技大学,四川 绵阳 621000)
滑坡泥石流风险防御工程效益评估的最优值距模型
乔建平1,2,黄 栋1,2,王 萌1,2,吴彩燕3
(1.中国科学院地表过程与山地灾害重点实验室, 四川 成都 610041; 2.中国科学院成都山地灾害与环境研究所, 四川 成都 610041;3.西南科技大学,四川 绵阳 621000)
本文在建立风险防治工程投资效益比(λ)、风险损失比(μ)、风险折减率(ΔR)3项评价指标后,首先建立单项指标效益的评价模型及评判标准,其次分别按3项效益指标内容对滑坡泥石流风险防御工程治理效益进行单项统计,最后应用最优值距离法综合分析3项指标统计结果,并给出5级效益评判标准。经过实例应用,该方法量化程度高、可靠性增强、具有较强的客观性,有一定的应用价值。
滑坡;工程;效益;最优距
E-mail:jpqiao@imde.ac.cn
0 引言
滑坡、泥石流风险管理中,对直接危害人命财产安全的灾害体一般都需要采取防御措施。防御措施中因灾害类型不同,危害程度不同,可以选择多种有针对性的工程措施或非工程措施。工程措施的类型包括:滑坡抗滑挡墙、抗滑桩等,泥石流的防御措施包括拦砂坝、排导槽等。非工程措施类型包括:监测预警,群测群防等。尽管在防御工程实施前,都要进行工程效益评估,但以往的工程效益分析仅仅采用工程投资效益比单项指标评估。这种方法过于简单,人为因素很重,评估结果不尽客观完善,因此可能影响科学合理的工程效益分析和投资决策。到目前为止,虽然国家还没有专门的地质灾害防御工程效益评估标准[1-2],但已有众多学者对开展相关的研究[3-8]。通过不断地总结摸索,建立符合国情特点的地质灾害防御工程效益评估的标准,以便推广应用。根据作者的研究经验认为[9],单体滑坡泥石流的风险防御工程效益评估相比区域效益评估应该更精细,可以从风险防御工程投资效益、风险损失、工程防御风险折减率三方面结果综合分析,最终评估风险防御工程的效益。这样可能客观的评估风险防御工程的实际价值。同时评估方法还应该符合简单易掌握,具有可操作性,评价指标易于采集统计,评估标准合理的基本原则。
1 风险防御工程投资效益比(λ)
工程投资效益比是检验工程投资量与被保护对象固定资产的合理性标准。不同行业都应该建立同等的技术标准。滑坡泥石流防治工程既有经济效益问题,也还有社会效益问题。本文的投资效益比只针对经济效益比,不涉及社会效益。因为滑坡泥石流工程投资效益比体现了防治工程方案的合理性、经济性和可靠性。并非工程投资越高,工程方案就越好。应该根据灾害的破坏特点和发育规律,选取最优化、最经济、效果可靠的工程方案。滑坡泥石流防治工程标准可根据保护对象的重要性确定,比如参考滑坡泥石流防治工程等级标准评价工程投资效益比[1-2]。滑坡泥石流治理工程投资效益比代表工程投资占保护对象固定资产量比重关系,即:

(1)
式中:λ——投资效益比系数;
X——保护对象直接和间接固定资产总量/万元;
xi——治理工程投资量/万元。


表1 工程投资效益比评价标准Table 1 Project investment benefit evaluation standard
表1中的防治工程等级参考文献[1]、[2]的标准。比例系数区间、效益等级属人为划分及赋值(下表均同)。
2 风险降低比(μ)
滑坡泥石流采用了工程措施或非工程措施后,其风险应该较之前降低。前后损失量的改变也体现了防治工程的效益。本文采用风险降低比评价防治工程前后的损失变化量。风险降低比指假设存在风险降低的前提下,通过实施防治工程措施和非工程措施,风险降低范围改变后的损失量变化情况。因此风险降低比也是评价防治工程对减小风险降低贡献的一个标准。根据防治工程的性质,风险降低比分为工程措施和非工程措施两种类型。
2.1工程措施风险降低比
工程措施包括土木工程治理和生物工程治理,工程治理措施对减少风险的贡献可采用工程治理前后滑坡泥石流风险降低量的变化率检验。因工程治理后滑坡泥石流的风险区域面积都将由原来范围变小,相应的工程治理前后范围内的固定资产损失量应该得到改变。固定资产损失量的前后之比,可以成为评价风险降低变化的标准,即:

(2)
式中:μ——风险降低比系数;
R′——工程治理后可能的风险损失量;
R——工程治理前保护对象直接和间接固定资产可能遭受风险损失总量。
无论滑坡泥石流在实施工程治理后,不同风险区内可能遭受到财产损失量都应该比工程治理前有所减小。如果风险降低比系数μ越小,说明工程治理后风险区面积越小,可能造成的风险降低量也越小,工程治理的效果越明显。无论工程防治的等级大小,工程治理措施的风险降低比,都可以按工程治理前后风险区面积内的固定资产可能的损失量变化等级进行评价(表2)。

表2 工程措施风险降低比评价标准Table 2 Engineering measures risk loss thanevaluation standard
2.2非工程措施风险降低比
在无工程措施治理的灾害点,需要按非工程措施的风险降低比统计。非工程措施主要包括监测预警系统和群测群防两种类型,而非工程措施的投资效益,很难以按监测预警前后的风险区固定资产损失量的变化作为评价标准。如果成功进行了监测预警,可以避免或减轻人员伤亡和财产损失。如果没有及时进行预警,也可能造成极大的人员伤亡和财产损失。尽管有的学者采用经济评估的方法探讨了滑坡、泥石流监测预警效益评估,但这些方法的统计过于繁杂,难以在现实情况中应用[6]。在只有监测预警系统或群测群防的滑坡、泥石流灾害点,可以采用可靠度的方法评价监测预警系统或群测群防手段减少风险损失的效益。
非工程措施可靠度评价是在规定的时间范围内,检验系统成功预警的概率,用R(t)表示。如果在规定时间内,系统成功预警的次数占全部运行次数的百分率,即:
R(t)=p(T>t) (0≤t<∞)
用频率表示,在t=0监测预警系统开始使用,到t时刻有β(t)没有成功预警,ρ(t)次成功预警避险,则t时刻的监测预警系统可靠度函数估计值为:
(0≤t<∞)
(3)
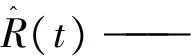
β(t)——未成功预警次数;
ρ(t)——成功避险次数;
N——预警总数。
当可靠度评价值越高时,风险降低率越低。非工程措施可靠度标准见表3。

表3 非工程措施可靠度评价标准Table 3 Non-engineering measures reliability evaluation standard
3 风险折减率(ΔR)
如前所述,当单体滑坡、单沟泥石流进行防治工程后,原有的风险降低率应该获得明显折减。将工程效益比和风险损失变化率两方面因素相结合,综合评价防治工程对减少灾害损失的贡献,可以使防治工程后的单体滑坡、单沟泥石流风险折减评估更具合理性和客观性。风险折减率可作为评估防治工程综合效果的一种标准,折减率越大,说明防治工程的效果越明显。
3.1工程措施风险折减率
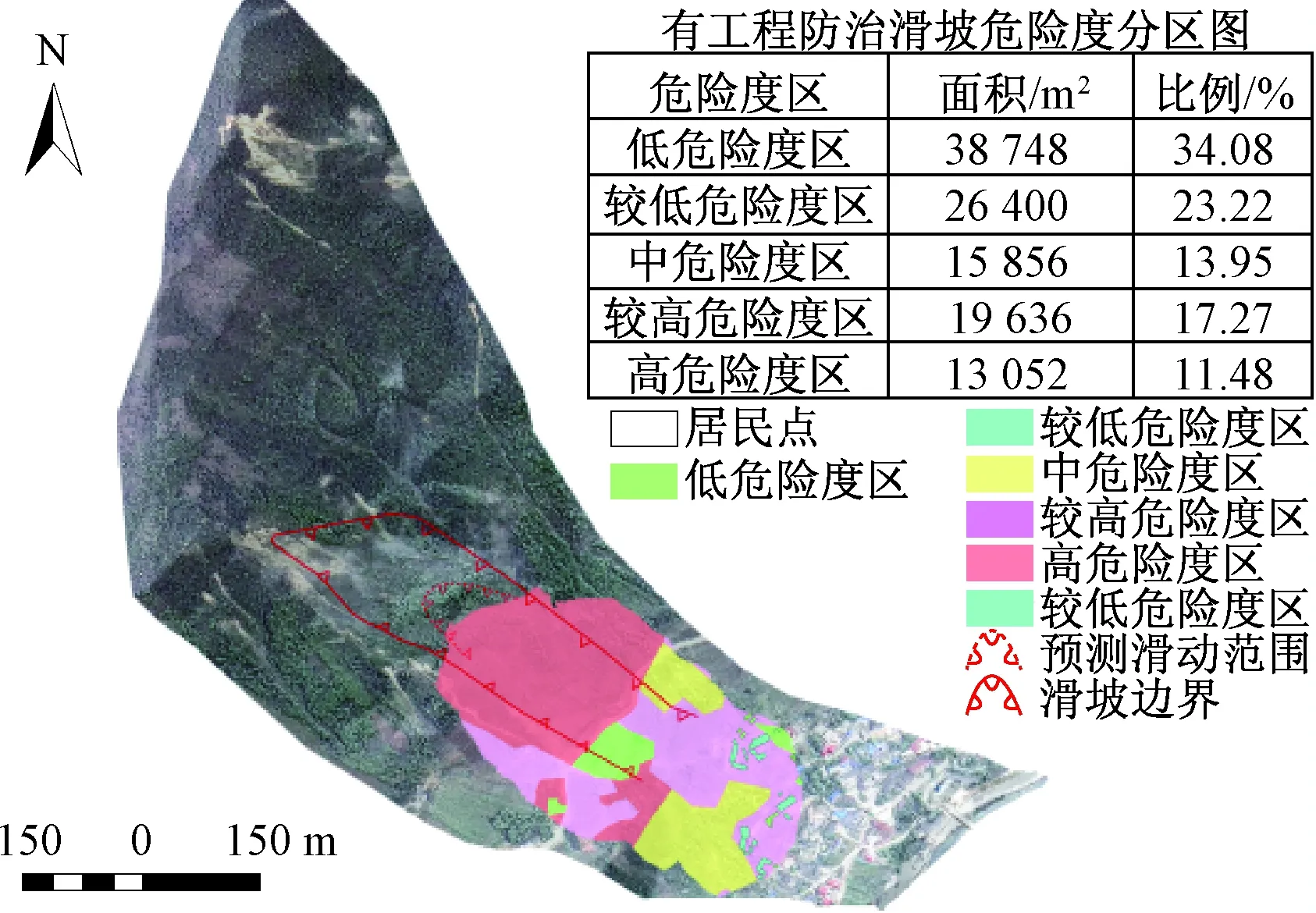
根据以上工程投资效益比及风险降低变化率评价标准,还可以建立滑坡泥石流进行工程治理措施后的风险折减率评价模型。如,假设某单体滑坡、单沟泥石流灾害的风险损失事件成立,无论风险损失程度如何,均可将该事件记作为:Rρ=1。进行工程治理后,经过对工程效益比(λ)和风险降低比(μ)进行综合评价,原有的风险将得到一定程度控制,其控制率可记为R0(0 ΔR(100%)=(Rρ-R0)·(100%)=(1-λ·μ)·(100%) (4) 式中:ΔR——风险折减率; Rρ——风险事件; R0——风险控制率。 如果统计的防治工程项目中既有工程措施,还包括非工程措施时,只需将非工程措施量计入工程总投资效益比即可。如果非工程措施费用太低,可以不计量。 根据表1、表2的评价标准,将表中数据代入式(4)可以建立工程措施的风险折减率评价标准(表4)。 表4的评价标准说明,当滑坡、泥石流灾害点进行工程治理后,风险折减率在90%以上时,其工程治理的效果是有意义的。风险折减率低于90%的工程治理效果都不是理想的效果。这意味存在一定的风险损失可能。 表4 工程措施风险折减率评价标准Table 4 Engineering measure risk loss reductionrate evaluation standard 3.2非工程措施风险折减率 (5) 式中:ΔR′——非工程措施风险折减率; 将式(3)可靠度代入式(5),可计算非工程措施折减率。 同上,根据表1、表3的评价标准,将表中数据代入式(5)也可以建立非工程措施的风险损失折减率评价标准(表5)。 表5 非工程措施风险折减率评价标准Table 5 Non-engineering measures risk lossreduction rate evaluation standard 对比表4与表5的标准,工程措施的风险折减率要求比非工程措施风险折减率更高。当工程措施的风险折减率达到80%以上时,其工程防御效果才是有意义的。而非工程措施风险折减率只要达到60%以上时,工程防御就已经发挥了应有的效果。因为工程措施的投入一般远大于非工程措施的投入量。所以应该具有更好的投资回报。 在完成上述单项指标评价的基础上,采用最优值距离法建立单项滑坡泥石流工程治理(工程措施及非工程措施)抗风险综合效益评估标准,检验工程治理对减轻风险灾害损失的综合效益贡献[10-12]。最优值距离评价模型,如: Δd=(1-d/D)·100 (6) 式中:Δd——综合评价值; d——实际统计值; D——最优值。 综合评估值为逆向指标,值越小,表示效益越好。评估值域应在(0,100)之间。以风险防御工程中的工程措施为例,将表1、2、4中单项评价等级赋值相加,获得工程综合效益最优值距离值为:D=15。对实际统计值:d=1~15采用式(6)可以建立抗风险综合效益评估数列:Δd=(0,0.14,0.20,…0.94)·(100),将这些数列的数据按5等级划分,得到工程治理抗风险综合效益评估标准(表6)。 表6 单体滑坡、单沟泥石流工程治理抗风险综合效益评估表Table 6 Monomer landslides, single gully control engineeringrisk comprehensive benefit evaluation table 当表6中最优距越小时,说明工程治理的抗风险综合效益越好。 选择汶川地震灾区都江堰市塔子坪滑坡为例,根据参考文献[13]的方法,采用式(7)的滑坡风险分布计算模型,即: (7) 将危险区(图1、图2)和易损区(图3、图4)分布实际计算数值代入式(7),可获得塔子坪滑坡工程治理前、后的风险分布图(图5、图6)。其中,工程治理前风险区分布面积为169 536 m2,工程治理后风险区分布面积为113 692 m2。 图1 工程治理前危险区分布图 图2 工程治理后危险区分布图 图3 工程治理前易损区分布图 图4 工程治理后易损区分布图 图5 工程治理前风险分布图 图6 工程治理后风险分布图 塔子坪滑坡工程治理前后的风险区范围得到明显改变(图5、图6),工程治理后尤其是中等以上风险区面积减小幅度最快,其中高风险区面积减小最明显。统计结果充分体现了工程治理的效益。 5.1工程投资效益比 塔子坪滑坡防灾工程包括了工程措施和非工程措施两项。其中工程措施费用共x1=650(万元、政府出资),非工程措施费用共x2=50(万元、成都山地所出资),保护对象的直接和间接固定资产的综合风险损失价值总量为:R=566.1(万元)。将三项费用代入式(1),可得工程效益比系数为: 塔子坪滑坡工程效益投资比系数为:λ=0.808,即保护对象的固定资产量仅占工程治理投资量的80.8%。参考表1评价标准为工程效益Ⅱ1-1级,即对Ⅲ级工程防治标准的工程投资效益比较高。 5.2风险降低比 5.2.1工程措施风险降低比 塔子坪滑坡防治工程措施实施前,在169 536 m2范围内可能遭受的直接和间可能遭受风险损失总量为:R=566.1万元。工程措施实施后,在113 692 m2范围内可能遭受的风险损失量为:R′=106.6万元。将工程措施前后的风险损失量代入式(2),可得降低比系数为: 参考表2工程措施风险降低比评价标准,损失比系数μ=0.163,属于工程效益等级的Ⅱ2-1级。即工程治理后,塔子坪滑坡风险降低效果好。 5.2.2非工程措施风险降低比 塔子坪滑坡防治既有工程措施,又有非工程措施。根据非工程措施风险降低比评价的原则,对进行工程治理的滑坡可以不考虑非工程措施风险降低。 5.3风险折减率 5.3.1工程措施风险折减率 根据式(5)的工程措施风险折减率计算方法,并分别将塔子坪滑坡的工程效益比系数λ及风险降低比系数μ代入该式,可获得工程措施风险降低率,即: ΔR(100%)=(R-R0)·(100%)=(1-λ·μ)· 计算结果,塔子坪滑坡进行工程治理后,风险折减率为86.9%。查表5获得折减率等级为Ⅳ4-1。即工程治理后,风险折减的效果比较明显。 5.3.2非工程措施风险折减率 塔子坪滑坡的非工程措施费用仅有50万。与工程措施总数相比数量太少。根据非工程措施风险折减率统计的原则,可以不考虑非工程措施的风险折减率。 5.4抗风险综合效益评估 根据式(6)评估模型,塔子坪滑坡抗风险综合效益为:2个Ⅱ级+1个Ⅳ级,将表1、2、4的等级赋值数代入,即: Δd=(1-d/D)·100=(1-10/15)·100=34符合表6的B级标准,工程治理抗风险综合效益好。 (1)地质灾害点经过风险评估后,根据风险损失的可能性应该加强风险防御工程处理。由于地质灾害防治的等级不同,保护对象的范围差异,防御工程的类型复杂,对防御工程的效益应该有一个客观、合理的综合性评估,分析投资的价值。 (2)以往仅仅通过单项指标,如投资效益比,评估地质灾害风险防御工程效益,是不能全面真实反映投资价值的。应该采用多指标综合统计分析的方法进行评估,这样才能客观分析防御工程的投资是否真正科学合理。 (3)论文采用投资效益比、风险降低比、风险折减率三项指标探讨了综合评估风险防御工程效益的方法。其方法简单、易操作、结果较客观,具有一定的应用价值。 (4)本评估方法中未考虑社会效益问题,还有待于今后进一步加强。 [1] 《地质灾害防治条例》中华人民共和国国务院令(第394号).2003. The geological disaster prevention and control regulations of the state council of the People′s Republic of China (No. 394). 2003. [2] 《地质灾害防治工程勘察规范》DB50/143-2003. The investigation of geological disaster prevention engineering DB50/143-2003. [3] 喻生波.地质灾害防治工程效益分析评价[J].甘肃地质,2009,18(2):75-77. YU Shengbo.Geological disaster prevention engineering benefit analysis evaluation [J].Geology in Gansu Province, 2009,18(2):75-77. [4] 刘友,王联军,余振国.地质灾害防治工程减灾经济效益评估理论探讨-以三峡库区地质灾害防治工程为例[J].中国国土资源经济,2007,20(10):39-41. LIU You, WANG Lianjun, YU Zhenguo. Geological disaster prevention engineering for disaster reduction economic evaluation theory to explore in the Three Gorges Reservoir geological disaster prevention engineering, for example[J].China′s Economy of Land and Resources, 2007,20(10):39-41. [5] 李彬,李丽华,王盼.地质灾害防治工程效益分析[J].资源环境与工程,2014,28(6):1211-1671. LI Bin, LI Lihua, WANG Pan.Geological disaster prevention project benefit analysis [J]. Resources Environment & Engineering, 2014,28(6):1211-1671. [6] 候俊东,候甦予,吕军,等.三峡库区地质灾害监测预警工程经济效益评估分析[J].中国地质灾害与防治学报,2012,23(2):64-69. HOU Jundong, HOU Gengyu, LYU Jun, et al. The Three Gorges Reservoir geologic hazard monitoring and early warning project economic evaluation analysis[J].The Chinese Journal of Geological Hazard and Control,2012,23(2):64-69. [7] 王念秦,周志强,王红兵.滑坡整治工程经济效益评估模式研究[J].甘肃科学学报,2002,14(3):78-84 WANG Nianqin, ZHOU Zhiqiang, WANG Hongbing. Landslide renovation engineering economic benefit evaluation model research[J].Journal of Gansu Science, 2002,14(3):78-84. [8] 张樑,梁凯.泥石流防治工程经济效益评价研究[J].中国地质灾害与防治学报,2005,16(3):48-53. ZHANG Liang, LIANG Kai.Economic evaluation of prevention projects of debris flow [J]. The Chinese Journal of Geological Hazard and Control, 2005,16(3):48-53. [9] 乔建平,王萌,吴彩燕.基于概率方法的区域地质灾害风险防御工程效益评估[J].中国地质灾害与防治学报,2017,28(2):131-136. QIAO Jianping, WANG Meng, WU Caixia. Preventing engineering benefit evaluation of rigional geological disaster risk based on probability method[J]. The Chinese Journal of Gedogical Hazard and Control,2017,28(2):131-136. [10] 孟涛.比较几种综合评价方法[J].淮北煤炭师范学院学报,2004,25(3):80-83. MENG Tao.Comparing several kinds of comprehensive evaluation method[J].Journal of Huaibei Coal Teachers College, 2004,25(3):80-83. [11] 杞娴,胡新俊.基于最佳距离度量近邻法的邻域风险最小化方法[J].云南大学学报:自然科学版,2004(5):373-377. QI Xian, HU Xinjun.Neighbor method based on optimal distance measure of neighborhood risk minimization method[J].Journal of Yunnan University: Natural Science Edition,2004(5):373-377. [12] 牛秀敏,郑少智.几种常规综合评价方法的比较[J].知识丛林,2006(3):140-143. NIU Xiumin, ZHENG Shaozhi. Several conventional comprehensive evaluation method of the comparison [J].Knowledge of The Jungle,2006(3):140-143. [13] 乔建平,黄栋,吴彩燕,等.地震扰动区单体滑坡风险评估[R].地震扰动区白沙河小流域滑坡、泥石流风险研究,2015:480-482. QIAO Jianping, HUANG Dong, WU Caiyan, et al. Seismic disturbance zone monomer landslide risk assessment [R]. Seismic Disturbance Zone White Sand River Watershed of Landslide Debris Flow Risk Research,2015: 480-482. Theoptimalvaluemodelforthebenefitfrommitigationmeasuresreducinglandslideanddebrisflow QIAO Jianping1,2,HUANG Dong1,2,WANG Meng1,2,WU Caiyan3 (1.KeyLaboratoryofGeo-SurfaceProcessandMountainHazards,CAS,Chengdu,Sichuan610041China; 2.InstituteofMountainHazardsandEnvironment,CAS,Chengdu,Sichuan610041,China; 3.SouthwestUniversityofScienceandTechnology,Mianyang,Sichuan621000,China) This paper proposed a method to evaluate the risk effectiveness of engineering prevention countermeasures for landslides and debris flows. Based on the evaluation model and index including benefit rate (λ), risk loss rate(μ)and risk reduction rate(ΔR)parameters, the risk effectiveness of disaster prevention countermeasures can be calculated according to the statistics of parameters, then risk effectiveness can be comprehensively evaluated by means of the optimum distance method, finally the evaluation of the risk effectiveness for landslides and debris flows engineering prevention countermeasures can be given by a effectiveness standard with 5 levels. According to the case study and application, this method is proved to be simple , objectivity, and applicable for practice. landslides; engineering countermeasures; risk effectiveness; optimum distance method P642.23 A 1003-8035(2017)03-0080-07 10.16031/j.cnki.issn.1003-8035.2017.03.12 2017-05-15; 2017-05-22 成兰铁路泥石流监测预警项目 乔建平(1953-),男,四川成都人,研究员,博士生导师,研究方向为滑坡规律、滑坡机理与滑坡危险度区划、地震滑坡。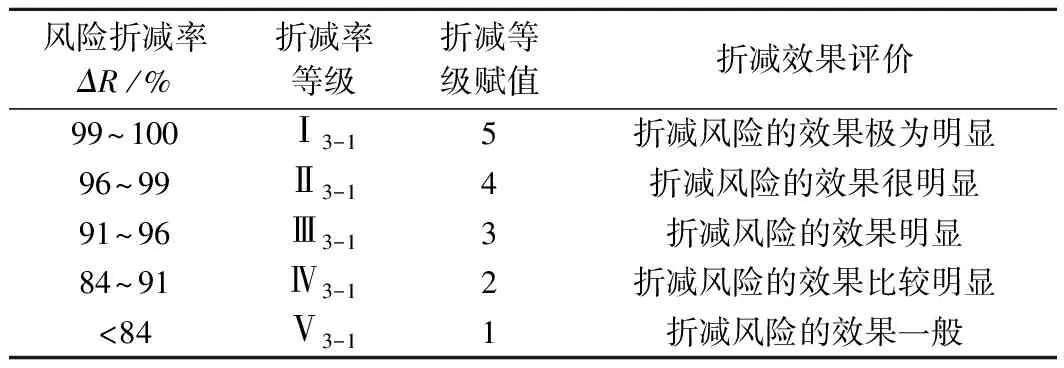
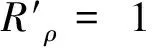


4 最优值距离效益评估模型

5 实例应用





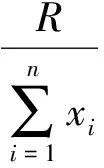

(100%)=(1-0.808×0.163)=0.8696 结语
