基于自抗扰控制的弹头制导与控制一体化设计

2017-11-07曹登庆黄文虎

宇航学报 2017年10期

关键词：观测器弹头制导

赵坤，曹登庆，黄文虎

(哈尔滨工业大学航天学院，哈尔滨 150001)

基于自抗扰控制的弹头制导与控制一体化设计

赵坤，曹登庆，黄文虎

(哈尔滨工业大学航天学院，哈尔滨 150001)

针对弹头再入过程中存在的强耦合、快时变以及气动参数摄动引起的不确定性等问题，采用自抗扰控制(ADRC)技术设计了再入弹头制导与控制一体化系统。首先建立了含不确定性参数、外界随机扰动以及通道耦合因素的，具有级联形式的制导与控制一体化动力学系统。然后根据级联系统的自抗扰控制方法对系统控制器进行分层设计，各层控制器之间彼此关联构成一体化控制系统。自抗扰控制器内嵌的扩张状态观测器(ESO)可对子系统各通道内的综合不确定性进行实时观测，并在误差反馈控制量中予以动态补偿，从而实现了各通道间的解耦控制。计算结果表明：设计的一体化控制系统能够适应各种复杂飞行环境下的导引需求，控制系统具有良好的动态特性和很强的鲁棒性。

再入弹头；制导控制一体化；自抗扰控制(ADRC)；扩张状态观测器(ESO)；BTT飞行器；不确定性

0 引言

现代战争中弹道导弹已经发展成为一种不可或缺的战略威慑武器。为了应对弹道导弹的威胁，美、俄、欧洲等相继建立了弹道导弹防御系统[1]。美国加紧部署的地基中段防御系统，形成了地基拦截、海基预警和天基跟踪监视的“多层”防御体系，对来袭的战略性弹道导弹在主动段、中段和再入段实行全方位拦截。弹头机动可以有效的躲避反导系统的拦截，被认为是最有效的突防技术之一[2]。倾斜转弯(Bank-to-turn，BTT)技术是用来提升弹头机动性能的重要方法之一。它与传统的侧滑转弯技术的不同在于：弹头转弯机动所需的向心力是通过弹体的滚转改变升力方向来实现的。但是弹头的滚转运动导致偏航通道和滚转通道出现严重的耦合效应，这是弹头控制系统设计面临的一大挑战。通常导弹制导与控制系统的设计是基于级联系统频谱分离假设，忽略制导系统(外环)与控制系统(内环)之间的耦合关系，采用二者分离再匹配联调的设计方法，这对于机动能力有限的低速导弹是有效的。然而弹头末端再入具有飞行速度快、飞行包线大、强耦合和快时变的特点，频谱分离假设不再成立[3]。传统的分离设计方法将导致再入弹头末端制导出现较大的脱靶量，弹体姿态控制效果不佳，不能满足终端落角约束等问题。

日益复杂的现代战场环境对弹头打击的精度要求也越来越高，近年来制导与控制一体化设计方法得到了国内外学者的普遍关注[4-8]。制导与控制一体化概念提出于上世纪80年代[4]，一体化设计过程中充分考虑了制导回路和控制回路的耦合关系，通过弹目相对运动关系和弹头动力学系统直接产生控制执行机构(舵面)所需的操纵指令。制导与控制一体化设计能够显著地缩短系统设计周期和降低研制成本，可使弹头导引和控制系统的整体性能得到大幅提升[5]。常见的制导与控制一体化设计方法包括小增益理论[6]、变结构控制[8]、最优控制[4,10]、Backstepping方法[11]和反馈线性化[12]等。受制于控制算法的复杂性，相关文献在一体化系统设计时一般将耦合项、不确定项以及干扰项视为小量或直接忽略再进行解耦设计，制导控制一体化的优势并没有得到充分展现。有学者提出在传统控制方法的基础上采用状态观测器对系统内的不确定性进行实时观测，然后在控制量中进行动态补偿的一体化设计思路。典型的状态观测器包括：非线性扰动观测器[7]、二阶滑模观测器[13]、高增益观测器[14]等。但上述状态观测器的构建均依赖于精确的数学模型和未知扰动边界，所以此类观测器的设计能力较差。张尧等[3]、孙向宇等[15]等在变结构控制的基础上采用扩张状态观测器(Extended state observer，ESO)对级联系统内存在的累积不确定性进行估计并在反馈控制中加以补偿，最终取得了良好的控制效果。

现代飞行器控制面临的一个突出难题在于如何对复杂飞行环境下出现的快时变、强耦合、强非线性等带来的大范围不确定性动态进行有效地控制[16]。自抗扰控制(Active disturbance rejection control，ADRC)技术是解决大范围及复杂结构不确定系统控制问题的有效方法得到了广泛的应用。弹头末端再入过程中由于高度、风速和大气密度等变化剧烈，气动参数和气动力矩参数均为状态量的复杂不确定函数。鉴于ESO良好的观测性能，我们提出采用ADRC对再入弹头一体化系统进行设计。实际上ESO内嵌于ADRC，它是ADRC算法的核心。ESO的设计独立于被控对象的数学模型，它可以将系统存在的耦合项、外部有界扰动以及系统内未建模动态等进行合并，然后统一扩张成新的状态量再进行估计。ADRC通过输出反馈对由ESO估计得到的系统不确定性动态进行实时的抑制或消除，从而实现对一体化系统的有效控制。ADRC不需要精确的模型信息，而且算法结构简单特别适合于工程应用[16]。文献[17-19]通过模型简化建立了含建模误差和不确定性的单通道一体化模型，在此基础上设计了三个彼此相关的自抗扰控制器构成一体化控制系统。但由于模型简化的需要，对一体化系统的耦合因素和不确定性忽略较多，不能充分体现一体化系统的优势。本文以再入弹头俯冲攻击地面固定目标为研究背景，充分考虑了再入弹头采用BTT机动控制引起的通道间耦合效应、大空域飞行带来的气动参数摄动以及外界随机扰动等因素，通过采用ADRC方法设计具有良好动态特性和鲁棒性的一体化控制系统。

1 数学模型和问题描述

1.1三维寻的制导数学模型

再入弹头末制导段的三维空间弹目运动关系如图1所示。其中，o为弹头质心，T为目标质心；oxyz为地面坐标系；oxLyLzL为视线坐标系，oxL轴与与弹目视线重合，由弹头指向目标为正，oyL轴位于包含oxL轴的纵向平面内，与oxL轴垂直，指向上方为正，ozL轴方向按右手定则确定；r为弹头与目标的距离；ε和η分别为导弹与目标之间的视线倾角和视线偏角。

参照文献[9]建立弹头与目标的相对运动模型，

(1)

式中：ar、aε和aη分别为弹头相对于地面的加速度在视线坐标系下沿oxL、oyL和ozL轴的投影。弹头末端采用倾斜转弯机动飞行时，一般采用倾侧角γv和攻角α为控制变量，因此需要进行控制变量的转换。首先，将速度坐标系下的加速度[axayaz]T投影到视线坐标系，

(2)

其中：C1为视线坐标系和地面坐标系之间的转换矩阵；C2为地面坐标系和速度坐标系之间的转换矩阵。一般认为沿着弹头速度轴的阻力X与发动机推力P平衡，因此弹头沿速度轴的速度vm不变，即ax为零。而

(3)

式中：m为弹头质量；Y为弹头的气动升力。将式(2)和式(3)代入式(1)，整理得

(4)

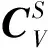
(5)

1.2制导与控制一体化模型

(6)

式中：

同时，根据弹头姿态运动学和姿态动力学方程，弹头非线性动力学模型为[9]

(7)

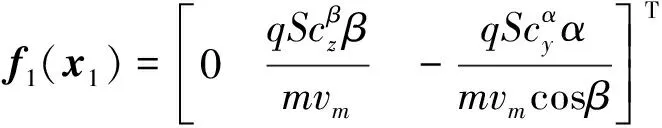
最后，对式(6)和式(7)进行归纳，得到再入弹头的制导和控制一体化动力学系统为

(8)

Γ=Γ0[1+Δmax·n(t)]

(9)

的形式。其中：Γ0为气动参数标称值，Δmax为对应气动参数的最大摄动百分比，n(t)为摄动函数，且有|n(t)|≤1。将(9)式代入式(8)，一体化动力学系统改写为

(10)

式中：G0、G1和G2分别为系统(8)中g0(t)、g1(ϑ,x1)和g2(t)的标称部分，且G1=g1(ϑ,x1)；F0、F1和F2为系统内的综合不确定项，其表达式分别为

(11)

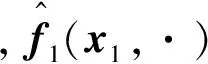
式(10)表明：制导与控制一体化系统为典型的级联系统。所谓级联系统就是控制器u直接驱动x2，而x2再去直接驱动x1，然后再由x1直接驱动x0，最终的控制目的是让x0跟踪时变轨迹v(t)，如图2所示。另外，一体化系统(10)中的各个子系统均为多输入-多输出的耦合系统，多变量系统的解耦控制也是亟待解决的重要问题。

2 基于ADRC的一体化系统控制算法

2.1自抗扰控制器的设计原理

自抗扰特性指的是实时估计扰动的功能及补偿的功能。具有这两个功能的控制器就可以称为自抗扰控制器[16]。

如图3所示，ADRC主要由跟踪微分器(Tracking differentiator，TD)、非线性状态误差反馈(Nonlinear state error feedback，NLSEF)和扩张状态观测器(ESO)三部分组成。ADRC将跟踪目标值v、系统的输出y和前一步的控制量u作为其输入，然后生成新的控制量的方法。对误差反馈控制量u0用扰动估计值zn+1的补偿来决定最终的控制量，即

(12)

式中：参数b0是决定补偿强弱的补偿因子，作为可调参数来用。相比于传统的控制方法，ADRC中增加了控制变量u的反馈通道，这正是ADRC具备自抗扰能力的根源。

2.2级联系统自抗扰控制器设计

对于级联系统(10)，可根据子系统的具体结构进行控制器的分层设计。假定所有状态变量x0，x1和x2都能够量测，把状态变量x1和x2依次当做控制状态变量x0和x1的虚拟控制量u0和u1，然后依次决定虚拟控制量ui(i=0, 1)，即把xi+1当做控制状态变量xi的虚拟控制量ui。一旦确定了虚拟控制量ui，就将其当做状态变量xi+1的目标轨线。这样依次下去最后可确定出实际的控制量u。

根据一体化系统设计的目标和级联系统的特点，设计三层自抗扰控制器—Layer 1、Layer 2和Layer 3组成制导与控制一体化系统，其结构如图4所示。下面将根据各子系统的具体结构分层构建相应的自抗扰控制器。

2.3多变量系统的解耦设计

2.3.1 第一层控制器(Layer 1)设计

本文研究的再入弹头寻的制导是对落地弹道倾角有约束的导引规律。为了保证攻击效果，再入弹头以特定角度打击地面目标，弹头的终端期望状态为

(13)

式中：tf为终端飞行时间；γDf为期望的终端弹道倾角。为同时满足式(13)中的终端约束条件，在此采用变结构控制方法进行导引律的设计，对于子系统中存在的综合不确定性F0(x0,t)采用ESO进行观测并在控制律中进行动态补偿。选择如下的滑模面切换函数

(14)

(15)

式中：k=diag(k01,k02)，λ=diag(λ01,λ02)，k0i、λ0i均为大于零的常数。该趋近律可确保系统在有限时间内到达滑模面，而且到达过程中具有良好的动态品质。

采用二阶ESO对一体化系统(10)的第1层中的综合不确定性F0(x,t)进行估计：

(16)

(17)

对式(14)求导，并结合式(1)、(15)和(16)，求得第1层虚拟控制量的表达式

(18)

2.3.2 第2层控制器(Layer 2)设计

(19)

为满足协调转弯的要求，令βc恒等于0。

针对一体化系统(10)中的第二层子系统把x2作为虚拟控制量，令x1跟踪第一层得到的虚拟控制量x1c。把系统控制量之外的模型部分F1(x1,t)称为动态耦合部分，引入虚拟控制量U1=G1x2，该部分为静态耦合部分。将第2层子系统写作如下形式：

(20)

利用ADRC技术进行多变量系统的解耦控制。系统(20)中的第i个通道的输入-输出关系为

(21)

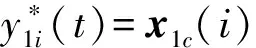
(22)

(23)

计算得出。

2.3.3 第3层控制器(Layer 3)设计

与第2层控制器的设计过程类似，u为实际控制量，令x2跟踪第2层得到的控制量x2c。引入本层的虚拟控制量U2=G2u，将第3层子系统表示为

(24)

继续利用ADRC技术进行多变量系统的解耦设计。系统(24)中的第j个通道的输入-输出关系为

(25)

(26)

如图6所示，在控制向量U2和输出向量y2之间并行地嵌入j个ADRC可以达到多变量系统解耦控制的目的。最后，实际的控制量u可由虚拟控制量U2由公式

(27)

计算得出。

3 仿真校验

为了验证本文提出的基于自抗扰控制的再入弹头制导与控制一体化设计方法的有效性，针对某型号弹头俯冲攻击地面固定目标的任务为例进行分析。

3.1仿真条件设置

本文在数值计算中用到的再入弹头的气动参数和结构参数的标称值如表1所示。

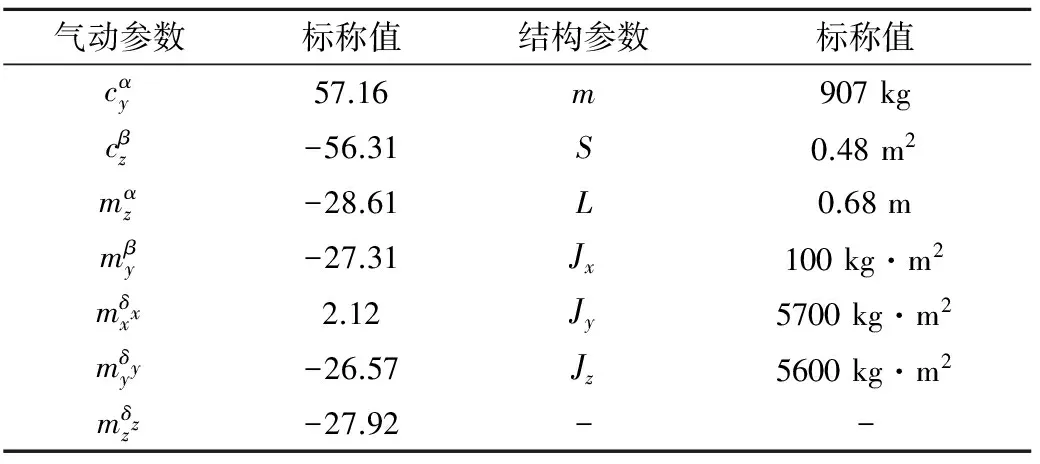
表1 弹头的气动参数和结构参数标称值[9]Table 1 Nominal values of aerodynamic and structure parameters of warhead[9]

由于再入过程中弹头的高度变化剧烈，因此必须考虑大气密度的变化。一般在0～80 km范围内，弹头所在位置的大气密度与高度的关系为

ρ=ρ0e-βy

(28)

式中：ρ0=1.225 kg/m2为零高度时的大气密度；β近似为一常数，通常取1/72001 m-1；y为弹头的飞行高度。

为保证再入过程中弹头姿态的稳定，需要对弹头姿态角、姿态角速度以及控制执行机构的偏转角进行约束。再入弹头采用BTT-90控制方式，最大滚转角γmax=90°；BTT-90弹头具备产生正负升力的能力，攻角的幅值约束为|α|≤15°；控制执行机构的偏转角范围限幅为±30°。

再入任务初始参数设置如表2所示。其中：θ和σ分别为弹头初始弹道倾角和弹道偏角。为比较方便，设置目标位置在地面坐标系的原点(0,0,0)处，为增加弹头的打击效能，设置弹头终端速度倾角为85°。

表2 再入弹头的初始状态Table 2 The initial state of a reentry warhead

基于ADRC的制导与控制一体化系统中各层的参数设置如下：

为增加气动系数建模的准确性，气动参数的最大摄动百分比统一取Δmax=30%，摄动函数n(t)=0.5sin(πt)。而外界的随机扰动dk(t)取为强度0 dBW的高斯白噪声(White Gaussian noise，WGN)，其中k=1,2,3。

3.2控制系统性能分析

图7为弹头再入过程中的空间飞行轨迹。计算结果表明：当终端位置偏差为3.3 m时，一体化控制系统进入制导盲区，当地弹道倾角偏差为0.76°，满足导引要求。图8为再入过程中弹头的姿态角时间历程曲线。再入初期：弹头与目标之间存在较大的视线角偏差(η0=-39.8°)，ADRC控制滚转角γ迅速翻转，随后弹头朝目标方向机动转弯；再入后期：随着滚转角不断地调整，弹头指向逐渐向目标方位收敛，γ趋于0。与此同时，设计的CBTT控制系统对侧滑角β的抑制效果显著，再入全程侧滑角始终维持在0°附近，满足协调转弯的要求。图9为再入过程中弹头机动过载的时间历程，弹头倾斜转弯调整航向时，产生了较大的侧向过载nz，航向调整结束后弹头停止滚转，侧向过载为0。

弹头调整航向的同时，ADRC还不断地对攻角α进行调整，以产生满足制导律要求的法向过载。再入初始弹道倾角为0°，弹头沿水平面xoz飞行，ADRC调整攻角为负值(图8)，进而在俯冲平面内产生负升力(图9，ny<0)，这样就迫使弹头速度方向下压，配合制导律向目标俯冲。再入全程为抵消气动参数摄动的影响，攻角不断进行适应性调整，最终得到的再入弹道平滑，弹头需用过载变化平缓，有效地消除了气动参数摄动的影响。从图8还可以看出，Layer 2中设计的ADRC对Layer 1中产生的控制指令跟踪准确，并且响应速度快、稳定性好。

再入弹头姿态角速度时间历程如图10所示。图10中，灰色曲线为Layer 2中ADRC产生的控制指令，为抵消外界的随机扰动以及气动参数摄动的影响，ADRC通过内嵌的ESO进行实时估计。以俯仰通道ωz为例，图11为控制过程中ESO对综合不确定项f2(ωz)的观测结果，灰色曲线为f2(ωz)的实际值，黑色部分为ESO的估计值。ESO不仅能够对气动参数摄动进行准确地估计，局部放大图显示ESO对随机扰动也具有极佳的观测效果。ADRC所具备的“自抗扰”功能得益于ESO优异的状态估计能力，然后在控制量的计算中得到了精确补偿。

对于单级不确定性系统而言，ADRC良好的“自抗扰”功能可使系统得到精确的控制，但对于级联系统“自抗扰”功能会产生级间的累积误差。为抵消本层的不确定性，ADRC对ESO的观测结果进行反馈补偿，这样不确定性就被间接地引入到了控制量中；下一层ADRC再对上一层控制量进行观测和补偿，这样上层不确定性又传递到了下层控制量中并逐级累积。为阻断不确定性在级间的传递，我们在ADRC中引入惯性滤波器，将各子系统中不利的随机不确定性从中剔除，图10中黑色曲线为Layer 3的ADRC对Layer 2产生的控制指令跟踪结果。带有惯性滤波器的ADRC不仅能够快速地跟随上层控制指令，并且有效的阻断了随机不确定性在级间的传递。

图12为弹头控制执行机构(舵面)的时间历程。再入全程各舵面响应迅速、输出稳定并且舵偏角均在约束范围内。根据ADRC技术设计的一体化控制系统实现了滚转、偏航和俯仰通道的解耦控制。弹头进行BTT机动时，ADRC能够使各舵面协调动作，即通过操纵滚转舵δx跟踪滚转指令的同时，还通过对方向舵δy的调整来抑制侧滑角，这样就有效地避免了运动耦合的发生，最终使弹头达到了协调转弯的目的。

3.3制导性能分析

为进一步验证一体化系统的制导性能，选择以下3种再入初始条件分别进行解算：

条件1：θ=-10°，σ=-150，γDf=-85°；

条件2：θ=0°，σ=-180°，γDf=-60°；

条件3：θ=10°，σ=-200°，γDf=0°；

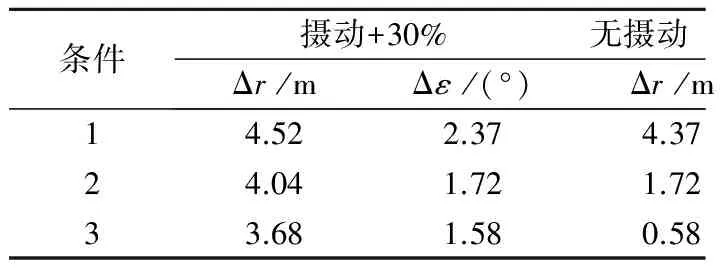
表3 弹头的制导性能指标Table 3 Guidance performance index of warhead

图13为不同初始条件下的再入弹道，计算结果表明各项制导性能指标均能满足导引需求，各项制导指标如表3所示。另外，表中还给出了相同再入条件下无气动参数摄动情况时的制导性能指标。对比结果表明，在气动参数摄动情况下取得的各项指标与无气动参数摄动情况的水平相当，均满足导引需求。具备抗干扰特性的一体化系统更符合工程实际，具有更好的工程实用性价值。

4 结论

本文基于ADRC技术设计了考虑外界随机扰动、气动参数摄动以及通道耦合因素的制导控制一体化系统。通过数值仿真校验了一体化系统可以满足终端落角约束条件并且具有较高的导引精度。一体化系统能够适应各种复杂飞行环境下的导引需求，控制系统具有良好的动态特性和很强的鲁棒性。所提方法能够从整体上协调制导系统和控制系统以及弹头动力学系统内部通道之间的关系，有效地提升了系统的整体性能。综合考虑控制系统的稳定性、动态特性、抗干扰性以及鲁棒性等方面，ADRC是一种很有前景的再入弹头一体化控制系统设计方法。

[1] 李林. 弹道导弹弹头机动突防研究[D]. 哈尔滨: 哈尔滨工业大学, 2011. [Li Lin. Research of ballistic missile warhead′s maneuvering penetration [D]. Harbin: Harbin Institute of Technology, 2011.]

[2] 崔静. 导弹机动突防理论及应用的研究[D]. 北京: 北京航空航天大学, 2001. [Cui Jing. Research on theory and application of missile maneuver penetration [D]. Beijing: Beihang University, 2001.]

[3] 张尧, 郭杰, 唐胜景,等. 导弹制导与控制一体化三通道解耦设计方法[J]. 航空学报, 2014, 35(12):3438-3450. [Zhang Yao, Guo Jie, Tang Sheng-jing, et al. Integrated missile guidance and control three-channel decoupling design method [J].Acta Aeronautica et Astronautica Sinica, 2014, 35(12):3438-3450.]

[4] Xin M, Balakrishnan S N, Ohlmeyer E J. Integrated guidance and control of missiles with method [J]. IEEE Transactions on Control Systems Technology, 2006, 14(6):981-992.

[5] Shima T, Idan M, Golan O M. Sliding-mode control for integrated missile autopilot guidance [J]. Journal of guidance, control, and dynamics, 2006, 29(2): 250-260.

[6] Yan H, Ji H. Integrated guidance and control for dual-control missiles based on small-gain theorem [J]. Automatica, 2012, 48(10): 2686-2692.

[7] 舒燕军, 唐硕. 轨控式复合控制导弹制导与控制一体化反步设计[J]. 宇航学报, 2013, 34(1):79-85. [Shu Yan-jun, Tang Shuo. Integrated guidance and control back-stepping design for blended control missile based on NDO [J]. Journal of Astronautics, 2013, 34(1):79-85.]

[8] 董飞垚, 雷虎民, 周池军,等. 导弹鲁棒高阶滑模制导控制一体化研究[J]. 航空学报, 2013, 34(9):2212-2218. [Dong Fei-yao, Lei Hu-min, Zhou Chi-jun, et al. Research of integrated roboust high order sliding mode guidance and control for missiles [J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(9):2212-2218.]

[9] 侯明哲. 寻的导弹导引与控制一体化设计[D]. 哈尔滨: 哈尔滨工业大学, 2011. [Hou Ming-zhe. Integrated guidance and control for homing missiles[D]. Harbin: Harbin Institute of Technology, 2011.]

[10] Yan H, Wang X, Yu B, et al. Adaptive integrated guidance and control based on backstepping and input-to-state stability [J]. Asian Journal of Control, 2014, 16(2): 602-608.

[11] Hwang T W, Tahk M J. Integrated backstepping design of missile guidance and control with robust disturbance observer [C]. International Joint Conference, Busan, South Korea, October 18-21, 2006.

[12] 尹永鑫, 杨明, 王子才. 导弹三维制导控制一体化设计[J]. 电机与控制学报, 2010, 14(3):87-91. [Yin Yong-xin, Yang Ming, Wang Zi-cai. Three dimensional guidance and control for missile [J]. Electric Machines and Control, 2010, 14(3):87-91.]

[13] 葛连正, 沈毅, 院老虎. 前向拦截的三维制导模型及制导律设计[J]. 系统工程与电子技术, 2008, 30(6):1118-1121. [Ge Lian-zheng, Shen Yi, Yuan Lao-hu. Three-dimensional guidance model and guidance law design for head pursuit interception [J]. Systems Engineering and Electronics, 2008, 30(6): 1118- 1121.]

[14] 马克茂, 马杰. 机动目标拦截的变结构制导律设计与实现[J]. 宇航学报, 2010, 31(6):1589-1595. [Ma Ke-mao, Ma Jie. Design and implementation of variable structure guidance law for maneuvering target interception [J]. Journal of Astronautics, 2010, 31(6):1589- 1595.]

[15] 孙向宇, 晁涛, 王松艳,等. 考虑通道耦合因素的制导控制一体化设计方法[J]. 宇航学报, 2016, 37(8):936-945. [Sun Xiang-yu, Chao Tao, Wang Song-yan, et al. Integrated guidance and control design method considering channel coupling [J]. Journal of Astronautics, 2016, 37(8):936-945.]

[16] 韩京清. 自抗扰控制技术—估计补偿不确定因素的控制技术[M]. 北京：国防工业出版社, 2008：221-237.

[17] 王冬, 侯明善, 周涛,等. 基于自抗扰的导弹一体化制导控制设计研究[J]. 电子设计工程, 2014, 22(20):62-66. [Wang Dong, Hou Ming-shan, Zhou Tao, et al. Integrated guidance and control design for missile based on ADRC [J]. Systems Engineering and Electronics, 2014, 22(20):62-66.]

[18] 董朝阳, 程昊宇, 王青. 基于自抗扰的反步滑模制导控制一体化设计[J]. 系统工程与电子技术, 2015, 37(7):1604-1610. [Dong Chao-yang, Cheng Hao-yu, Wang Qing. Backstepping sliding mode control for integrated guidance and control design based on active disturbance rejection [J]. Systems Engineering and Electronics, 2015, 37(7):1604-1610.]

[19] 王文文, 刘晓利, 李志坚. 基于自抗扰控制的微型导弹导引控制一体化设计[J]. 指挥控制与仿真, 2015, 3:121-125. [Wang Wen-wen. Liu Xiao-li, Li Zhi-jian. Integrated guidance and control of micro missile based on active disturbance rejection control [J]. Command Control & Simulation, 2015, 3:121-125.]

[20] 张靖男, 赵兴锋, 郑志强. BTT导弹的发展现状与趋势[J]. 飞航导弹, 2006, 10:37-39. [Zhang Jing-nan, Zhao Xing-feng, Zheng Zhi-qiang. Development status and trend of BTT missiles [J]. Winged Missile, 2006, 10:37-39.]

IntegratedGuidanceandControlDesignforReentryWarheadBasedonADRC

ZHAO Kun, CAO Deng-qing, HUANG Wen-hu

(School of Astronautics, Harbin Institute of Technology, Harbin 150001, China)

An integrated guidance and control system is designed based on the active disturbance rejection control (ADRC) method, which is aimed at the problems of strong coupling, fast time-varying, and uncertainty caused by aerodynamic parameter perturbation during the reentry of a warhead. Firstly, the integrated dynamics system of guidance and control with cascading form is established, which includes the parameter uncertainties and external random disturbances as well as channel coupling factors. Then, the controller of the system is hierarchically designed according to the ADRC method of the cascade system, and the controllers of each layer are associated with each other to form an integrated control system. The extended state observer (ESO) embedded in ADRC is employed to realize the real-time observation of the integrated uncertainties in each channel of the subsystem, and the results are used to compensate dynamically in the error feedback control quantity to achieve the decoupling control among the channels. The simulation results indicate that the designed integrated control system can adapt to the guidance requirements of various complex flight environments, and the control system has good dynamic characteristics and strong robustness.

Reentry warhead; Integrated guidance and control; Active disturbance rejection control (ADRC); Extended state observer (ESO); BTT vehicle; Uncertainty

V448.2

1000-1328(2017)10- 1068- 11

10.3873/j.issn.1000-1328.2017.10.007

2017- 06- 15;

2017- 08- 24

国家重点实验室开放基金(HIT.KLOF.2016.071)

赵坤(1988-)，男，博士生，主要从事航天器动力学与控制研究。

通信地址：黑龙江省哈尔滨市南岗区西大直街92号正心楼飞行器动力学与控制研究所(150001)

电话：18003656889

E-mail: zhaokunhit@yeah.net

曹登庆(1958-)，男，博士，教授，主要从事航天器动力学与控制研究。

通信地址：黑龙江省哈尔滨市南岗区西大直街92号正心楼飞行器动力学与控制研究所(150001)