一种高超声速飞行器鲁棒自适应控制方法
2017-11-07余朝军郑亚龙
余朝军,江 驹,肖 东,郑亚龙
(南京航空航天大学自动化学院,南京 211106)
一种高超声速飞行器鲁棒自适应控制方法
余朝军,江 驹,肖 东,郑亚龙
(南京航空航天大学自动化学院,南京 211106)
针对较强参数摄动情况下高超声速飞行器巡航段控制问题,提出一种基于主影响元素分析的鲁棒自适应控制方法。首先在飞行器具有未知参数情况下,使用符号计算工具对系统不确定量进行分离,实现不确定性的建模;进一步使用蒙特卡洛试验方法,确定不确定函数向量的主影响元素,对模型进行简化。然后在滑模控制的基础上,结合参数自适应估值和鲁棒补偿的方法,设计出飞行控制器,实现对未知参数的自适应估值以及对模型误差的补偿,并从理论上证明了系统的稳定性。仿真试验表明,在较大参数摄动情况下,文中所提方法依然可以保证系统的稳定性和跟踪性能。
高超声速飞行器;不确定性建模;主影响元素分析;鲁棒自适应控制
0 引 言
吸气式高超声速飞行器具有飞行包络大,速度极快,运载效率高等特点[1-2],使得其在太空探索以及军事应用上有着重要的研究意义。性能良好的控制器是高超声速飞行器能够顺利完成飞行任务的必要保证。由于高超声速飞行器具有飞行包络大,燃料消耗快,发动机和机身之间耦合作用强,气动加热效应明显以及试验数据不完备等因素[3],其具有不可忽视的不确定性。为了保证飞行控制器的有效性,必须在控制器设计层面上将这些不确定性因素予以充分考虑。
线性控制方法已很早应用于飞行控制器的设计。文献[4]通过分析模型不确定性来源,设计了基于线性二次型调节器的隐式模型跟随鲁棒协调控制器。文献[5]采用μ分析方法设计了高超声速飞行器鲁棒控制系统,一定程度上解决了高超声速飞行器控制系统存在多种不确定因素情况下的建模误差问题。文献[6-7]结合线性二次型最优控制器算法(Linear quadratic regulator,LQR),分别设计了自适应控制器和抗饱和控制器,以保证控制系统在不确定情况下以及输入受限情况下的性能。
然而高超声速飞行器具有高度非线性和强耦合的特点[3],使得基于小扰动线性化模型的线性控制方法难以保证飞行性能。所以很多的学者致力于研究高超声速飞行器的非线性控制方法。滑模控制[8-9],模糊控制[10],反步法控制[11-13]等非线性控制方法被大量应用于飞行控制器设计中,并取得了很多研究成果。其中鲁棒性和适应能力始终是高超声速飞行控制器设计中的一项核心研究内容。
文献[9]使用鲁棒自适应滑模控制技术保证了系统对模型不确定性和外部干扰的抵抗能力。文献[10]针对锥形体高超声速飞行器,使用模糊自适应的方法逼近系统不确定函数项,保证了系统的半全局最终一致有界。文献[11]使用Backstepping控制的思想设计速度子系统和高度子系统的控制器,通过结合自适应干扰上界估值和滑模控制技术,得到最终飞行控制器,该控制器可以在干扰上界未知情况下保证系统的稳定性。文献[12]利用指令滤波器获取虚拟控制量的一阶导数,解决了反演控制方法中的“微分项膨胀”问题,同时引入扩展状态观测器(Extended state observer,ESO)对模型中的不确定项进行估计和补偿,保证闭环系统在存在参数不确定和外部扰动的情况下仍具有较好的控制性能。文献[13]提出一种考虑耦合特性的新型鲁棒姿态控制律,结合反步控制和干扰观测器方法设计了鲁棒飞行控制器,保证系统的渐近稳定性和鲁棒性。文献[14]使用神经网络来逼近系统不确定性部分,使用了Nussbaum函数保证了系统在控制增益函数未知情况下的稳定性。文献[15]针对高超声速飞行器设计了一种基于有限时间收敛干扰观测器的鲁棒控制方法,既可以保证鲁棒性和干扰抑制能力又使系统具有较好的跟踪性能。文献[16]通过输出重定义的方法使非最小相位系统的不稳定零动态变为渐近稳定,采用切换控制方法消除系统不确定性带来的影响,提高了系统的鲁棒性。文献[17]采用反馈线性化实现姿态的解耦控制,然后设计了基于特征模型的自适应姿态控制律用以保证系统的鲁棒性与自适应性。
当高超声速飞行器具有较大的参数摄动时,一般的鲁棒控制方法难以保证系统性能。本文就该控制问题提出一种控制器设计思路。首先对系统模型进行详细的分析,进行不确定性建模;然后考虑到减少飞行控制器计算量的问题,设计出一种模型简化方法,对不确定模型进行主影响因素的提取和适当简化;然后结合滑模控制、参数自适应估值和鲁棒补偿的方法设计了一种鲁棒自适应控制器,用以消除参数不确定和模型误差的不利影响。
1 问题描述
高超声速飞行器纵向刚体动力学模型如下:
(1)
式中:V、γ、α、q、h分别为速度、航迹倾斜角、迎角、俯仰角速度和高度;g、Iy分别为重力加速度和绕y轴的转动惯量;L、D、T分别为升力阻力和推力。根据文献[18]可得气动力,气动力矩和发动机推力的拟合表达式如下:
(2)
(3)
大气密度ρ和重力加速度g可根据下式计算:
(4)
发动机动态采用如下二阶模型表示[18]:
(5)
式中:ωn=5,ξ=0.7,βc为发动机节流阀调定值的指令信号,可以通过调节βc来控制发动机的推力大小。
本文主要考虑高超声速飞行器在参数不确定情况下的控制问题。根据已有的关于这种飞行器的经验和数据,考虑系统具有以下惯性参数,几何参数,环境参数和气动参数的摄动:
(6)
控制器设计目标是在系统的以上参数具有较大的摄动时,设计控制器保证系统的稳定性和跟踪性能。
2 不确定性建模与化简
2.1不确定性建模
易知,高超声速飞行器模型可以表示为如下非线性系统
(7)
通过验证可知该系统对于速度和高度的相对阶次分别为3和4。所以当考虑到参数不确定时,对速度和高度分别进行求导三次和求导四次的处理,并且对不确定项进行分离,则系统可转化为如下不确定模型形式:
(8)

使用Matlab软件的符号计算功能对φi的表达式进行计算,从而得到不确定模型。由于符号计算所得的表达式过长,无法在文中列出,所以在表1中给出计算结果的相关信息。由表1可知,这些函数向量的表达式长度很长,即模型的复杂程度很高,直接对此模型设计控制器会导致很大的计算量,不利于实现。

表1 Matlab符号计算结果的相关信息Table 1 Information of Matlab symbolic computing results
2.2主影响元素的分析与提取

在某一巡航飞行阶段,通过对飞行器可能到达的飞行状态以及系统未知参数取值范围的分析,可知飞行状态x和未知系统参数p应分布于如下状态集合Ωx和参数集合Ωp中。
(9)
在集合(9)中等可能性地随机选择足够多组状态和参数样本,并且按下式计算Λi和Πi:
(10)
(11)

通过对Πi不同维度上数值大小的分析可以发现,φi的绝大部分的不确定量是由少部分维度造成的。所以完全可以在控制器设计时忽略掉一些次要维度所对应的函数项,从而在减小计算量同时保证较高的模型准确性。通过保留前95%的不确定量产生因素,可以使得各个函数向量维度减少,得到其主成分的信息如表2所述。


表2 被保留函数向量的主成分的相关信息Table 2 Information of principal component dimension of reserved vector function
对比表1和表2中字符串长度一栏可知,ξi的计算量比φi减少了很多。在式(8)中用ξi替代φi即可得到简化的高超声速飞行器不确定模型,该模型具有较低的计算复杂度,同时可以保证较高的准确性。
3 鲁棒自适应控制器设计
在第2节得到的简化的不确定模型的基础上,本节结合积分滑模控制、参数自适应估值和鲁棒补偿的方法进行控制器的设计,来保证系统的稳定性以及消除参数摄动和模型误差的不利影响。
3.1控制器设计
通过第2节的分析,高超声速飞行器模型可转化为如下系统:
(12)
对模型(12)进一步整理得
(13)
设速度指令信号为Vc,高度指令信号为hc。令速度跟踪误差为eV=V-Vc,高度跟踪误差为eh=h-hc。
选取如下积分滑模面函数
(14)
对S求导数,可得
(15)
在有界参数摄动的情况下d是有界的,且其数值相对于被保留的主成分部分小很多。由于d为关于状态量以及参数摄动量的复杂表达式,其上界难以直接给出,所以可以做出如下假设。

针对不确定模型(12),设计如下所示控制律、自适应律和鲁棒补偿项。
控制律:
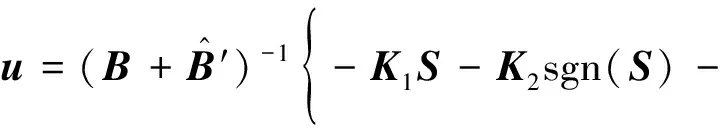
(16)
参数自适应律:
(17)
鲁棒补偿项:
(18)

3.2稳定性证明
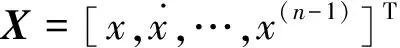
(19)
式中:i=0,1,…,n-1。
定理1. 对于参数不确定系统(12),选择滑模面函数(14),控制律(16),参数自适应律(17)和鲁棒补偿项(18),可以保证系统跟踪误差eh和ev最终一致有界,且当t→+∞时,稳态跟踪误差界为
(20)

证.选取李雅普诺夫函数如下
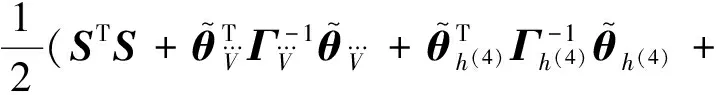
(21)
对Ve求导可得
(22)
将式(15)、(16)代入式(22)得
(23)
将式(17)代入式(23)得
(24)
将式(18)代入式(24)得
(25)
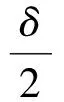
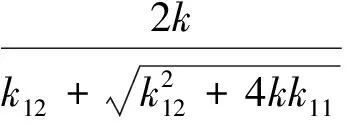
4 仿真分析

考虑在较大幅度的参数摄动情况下,高度和速度的指令跟踪控制仿真试验。所添加的参数摄动如下:
由于仿真主要考虑高度爬升的指令跟踪控制,为验证控制器性能,所以在仿真试验时加入了较大的升力系数的摄动。在实际控制系统中,为了解决滑模控制器抖振问题,采用了饱和函数来代替符号函数。仿真结果如图3~6所示。
图3是高度指令跟踪和速度保持的变化曲线,由于升力系数损失较大,所以在初始时刻飞行器有一个比较明显的快速下降趋势,通过控制器参数自适应调整,系统得以稳定,高度误差和速度误差最终趋于零。图4是γ、q和α的变化曲线,可以看出这些状态量在指令跟踪过程中变化比较平稳。图5是控制输入量的变化,可以看出升降舵和油门均在合理范围内平稳变化,且没有抖振现象。图6是滑模面函数的变化曲线。由SV和Sh的变化可知大概5 s之后系统已经达到滑模动态。总体而言,仿真结果表明,在较大参数摄动情况下,该控制方法依然可以保证系统的指令跟踪性能,同时过渡过程也比较平稳快速。
5 结 论
本文研究了高超声速飞行器参数不确定控制问题,提出一种鲁棒自适应控制器的设计思路。主要贡献如下:1)建立了高超声速飞行器参数不确定模型;2)设计了一种基于主影响因素分析的模型简化方法,可以减小模型计算量同时保证较高的模型准确性;3)针对所得到的简化高超声速飞行器模型,设计了一种鲁棒自适应控制器,该控制器可以在参数不确定和模型不确定并存的情况下,保证系统的稳定性。
[1] 崔尔杰. 近空间飞行器研究发展现状及关键技术问题[J]. 力学进展, 2009, 39(6): 658-673. [Cui Er-jie. Research statutes, development trends and key technical problems of near space flying vehicles [J]. Advances in Mechanics, 2009, 39(6): 658-673.]
[2] Hank J M, Murphy J S, Mutzman R C. The X-51A scramjet engine flight demonstration program [C]. The 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Ohio, USA, April 28-30, 2008.
[3] 黄琳, 段志生, 杨剑影. 近空间高超声速飞行器对控制科学的挑战[J]. 控制理论与应用, 2011, 28(10): 1496-1505. [Huang Lin, Duan Zhi-sheng, Yang Jian-ying. Challenges of control science in near space hypersonic aircrafts [J]. Control Theory and Applications, 2011, 28(10): 1496-1505.]
[4] 曲鑫, 李菁菁,宋勋, 等. 考虑推进和气动弹性影响的高超飞行器的建模与控制[J]. 宇航学报, 2011, 32(2): 303-309. [Qu Xin, Li Jing-jing, Song Xun, et al. Modeling and robust coupled control of air-breathing hypersonic vehicle considering propulsion and aeroelastic effects [J]. Journal of Astronautics, 2011, 32(2): 303-309.]
[5] 尉建利, 于云峰, 闫杰. 高超声速飞行器鲁棒控制方法研究[J]. 宇航学报, 2008, 29(5): 1526-1530. [Wei Jian-li, Yu Yun-feng, Yan Jie. Research on robust control of hypersonic vehicle [J]. Journal of Astronautics, 2008, 29(5): 1526-1530.]
[6] Gibson T E,Crespo L G, Annaswamy A M. Adaptive control of hypersonic vehicles in the presence of modeling uncertainties [C]. American Control Conference, St. Louis, USA, June 10-12, 2009.
[7] Groves K P,Serrani A, Yurkovich S, et al. Anti-windup control for an air-breathing hypersonic vehicle model [C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, Colorado, USA, August 21-24, 2006.
[8] 蒲明, 吴庆宪, 姜长生, 等. 基于二阶动态terminal滑模的近空间飞行器控制[J]. 宇航学报, 2010, 31(4): 1056-1062. [Pu Ming, Wu Qing-xian, Jiang Chang-sheng, et al. Near space vehicle control based on second-order dynamic terminal sliding mode [J]. Journal of Astronautics, 2010, 31(4): 1056-1062. ]
[9] 黄喜元, 王青, 董朝阳. 基于动态逆的高超声速飞行器鲁棒自适应控制[J]. 北京航空航天大学学报, 2011, 37(5): 560-563. [Huang Xi-yuan, Wang Qing, Dong Chao-yang. Robust adaptive control for hypersonic vehicle based on dynamic inversion [J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(5): 560-563.]
[10] 胡超芳, 刘艳文. 基于动态面的高超声速飞行器模糊自适应非线性控制[J]. 控制与决策, 2013, 28(12): 1849-1854. [Hu Chao-fang, Liu Yan-wen. Fuzzy adaptive nonlinear control based on dynamic surface control for hypersonic vehicle [J]. Control and Decision, 2013, 28(12): 1849-1854.]
[11] Zong Q, Wang F, Tian B, et al. Robust adaptive approximate backstepping control design for a flexible air-breathing hypersonic vehicle [J]. Journal of Aerospace Engineering, 2014, 28(4): 724-732.
[12] 董朝阳, 路遥, 王青. 高超声速飞行器指令滤波反演控制[J]. 宇航学报, 2016, 37(8): 957-963. [Dong Chao-yang, Lu Yao, Wang Qing. Command filtered backstepping control for hypersonic vehicle [J]. Journal of Astronautics, 2016, 37(8): 957-963.]
[13] 郭宗易, 周军, 郭建国. 新型高超声速飞行器耦合姿态控制系统设计[J]. 宇航学报, 2017, 38(3): 270-278. [Guo Zong-yi, Zhou Jun, Guo Jian-guo. Novel coupling based attitude control system design for hypersonic vehicles [J]. Journal of Astronautics, 2017, 38(3): 270-278.]
[14] Xu B. Robust adaptive neural control of flexible hypersonic flight vehicle with dead-zone input nonlinearity [J]. Nonlinear Dynamics, 2015, 80(3): 1509-1520.
[15] Yang J, Li S H, Sun C Y, et al. Nonlinear disturbance observer based robust flight control for air-breathing hypersonic vehicles [J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1263-1275.
[16] 路遥, 王青, 董朝阳. 输出重定义的高超声速飞行器鲁棒自适应控制律设计[J]. 宇航学报, 2014, 35(3): 331-339. [Lu Yao, Wang Qing, Dong Chao-yang. A study on output redefinition robust adaptive control method for hypersonic vehicle [J]. Journal of Astronautics, 2014, 35(3): 331-339.]
[17] 杜立夫, 黄万伟, 刘晓东, 等. 考虑特征模型的高超声速飞行器全通道自适应控制[J]. 宇航学报,2016, 37(6): 711-719. [Du Li-fu, Huang Wan-wei, Liu Xiao-dong, et al. Whole-channel adaptive control for hypersonic vehicle considering characteristic model [J]. Journal of Astronautics, 2016, 37(6): 711-719.]
[18] Xu H, Minmirani M D, Ioannou P A. Adaptive sliding mode control design for a hypersonic flight vehicle [J]. Journal of Guidance, Control, and Dynamics, 2004, 27(5): 829-838.
[19] 李鹏. 传统和高阶滑模控制研究及其应用[D]. 长沙: 国防科技大学, 2011. [Li Peng. Research and application of traditional and higher-order sliding mode control [D]. Changsha: National University of Defense Technology, 2011.]
ANovelRobustAdaptiveControlSchemeforHypersonicVehicles
YU Chao-jun, JIANG Ju, XIAO Dong, ZHENG Ya-long
(College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106,China)
A robust adaptive control method based on main influence elements analysis is proposed for the hypersonic vehicles in strong parameter perturbations case during the cruise phase. Firstly, under the condition of parameter uncertainties, symbolic calculation tools are used to separate the uncertainty terms, and the uncertainty model is obtained. Furthermore, Monte Carlo method is implemented to determine the main influence elements of the uncertainty function vectors, the uncertainty model is simplified. Secondly, on the basis of the sliding mode control, a flight controller is designed combining the parameter adaptive estimation and robust compensation, then the stability of system is proved theoretically. Lastly, a detailed simulation experiment is carried out, which verifies that the flight controller can guarantee system stability and tracking performance even in case of large parameter perturbations.
Hypersonic vehicles; Uncertainty modeling; Main influence element analysis; Robust adaptive control
V448.2
A
1000-1328(2017)10- 1088- 09
10.3873/j.issn.1000-1328.2017.10.009
2017- 05- 31;
2017- 08- 21
国家自然科学基金(61673209);南京航空航天大学研究生创新基地(实验室)开放基金(kfjj20160318);航空科学基金(2016ZA52009);一院高校联合创新基金(CALT201603)
余朝军(1994-),男,硕士生,主要从事先进飞行控制技术研究。
通信地址:江苏省南京市江宁区将军大道29号南京航空航天大学自动化学院4号楼(211106)
电话: 17751756263
E-mail: 1490273365@qq.com
