减阻增程弹道的射程估算与特性分析

凌王辉，鲜 勇，郭玮林，李 杰，张大巧

(火箭军工程大学七系，西安 710025)

减阻增程弹道的射程估算与特性分析

凌王辉，鲜 勇，郭玮林，李 杰，张大巧

(火箭军工程大学七系，西安 710025)

为实现弹道导弹射程的快速估算和减阻设计后弹道增程的定量分析，提出一种基于导弹基本参数的射程快速精确估算方法。通过建立减阻模型，仿真计算得到气动阻力系数表，并对速度计算公式进行逐项积分，利用高度近似值和气动系数拟合结果得到关机点状态量和射程的初步值，最终通过迭代计算得到满足精度要求的射程结果。仿真结果表明，经过高度和气动系数的迭代计算能有效快速得到满足精度的计算结果，通过减阻设计，导弹射程提高了162.36 km，增程的效果明显。

减阻设计；弹道增程；射程快速估算；气动拟合；迭代计算

0 引 言

导弹的射程决定了导弹的火力攻击范围，是衡量导弹性能的重要参数之一。导弹拥有更远的射程意味着在相同射程下，能投掷更大质量的战斗部，具有更多的能量进行机动突防[1-2]。自弹道导弹诞生以来，推进剂的推陈出新、材料的更新换代和外形结构的改型升级使导弹的射程得到不断提升，除此之外，通过外形减阻设计也可以达到提高射程的目的。美国的“三叉戟”Ⅰ型导弹就运用了激波杆设计，起到了减小大约52%阻力，增加550 km射程的效果。在此基础之上，其改进的“三叉戟”Ⅱ型导弹进一步扩大了头部的容积，增加了弹头的投掷数量[3]。

仿真计算和风洞试验表明，导弹的钝头体构型相比其余尖头体构型，受到的气动阻力最大[4]，加装激波杆能改变头部流场形态，形成斜激波，减小波后压力与焓值，有效减小气动阻力[5]。目前激波杆减阻的相关研究主要是实现减阻效果的仿真校验与外形机构的优化设计[6-7]，但是对减阻设计后弹道增程效果的分析研究却很少。

目前利用弹道基本参数实现射程估算的研究较为广泛，如文献[8]对模型和数据进行分离，设计了通用弹道仿真模型，实现了仿真多种弹道导弹弹道的功能，但此方法仍基于微分方程组的数值计算，计算量大，运算时间长；文献[9]基于固定类型导弹的推力加速度模板对导弹主动段运动特性进行了仿真计算，估算性能良好，但构建的近常速运动模型忽略了气动力，无法用于减阻与未减阻弹道的仿真对比。

而文献[10-11]针对助推滑翔式高超声速飞行器，根据其运动方程和飞行条件推导了估算公式，利用弹道参数对滑翔弹道进行了解析估算，并引入高度变化特性进一步提高了估算精度。基于此想法，本文以减阻设计的弹道导弹弹道为研究对象，根据飞行过程中的速度微分方程，推导了关机点状态的计算公式，利用迭代计算，进一步提高了射程的计算精度，并针对具体减阻构型，实现了减阻增程效果的定量分析。

1 减阻原理

由图1所示的流场示意图，钝头锥体前为弓形激波，激波杆钝头体的流场结构则由斜激波、分离区、剪切层和再附激波组成。

钝头体结构前，气流经过强烈压缩，形成弓形激波，与之相比，减阻杆破坏了弓形激波，形成斜激波。斜激波后的气流情况与弓形激波后的气流情况差异较大，因此导致二者头部的压力分布不同。根据普朗特关系式，斜激波后的气压远小于弓形激波后的气压，这使带减阻杆外形的头部压力远小于钝头锥体头部压力，因此减小了带激波杆外形的气动阻力。

2 仿真模型与网格

根据外形的具体设计参数，建立加装激波杆导弹的实体模型。带激波杆外形的模型如图2所示。

进行计算区域离散化，将连续的计算区域划分为多个子区域，确定每个区域中的节点，从而生成网格。本文采用O型的非结构网格，生成的网格如图3～4所示，其中图3为生成的总体网格，图4为物面处的网格，放大了非结构网格在物面处的细节，贴体性较好，密集均匀，能满足捕捉流场细节的需要。

3 估算方法

假设导弹在射面内飞行，如图5所示，则导弹的主动段质心运动方程为：

(1)

式中：V为导弹的速度，P为推力，m为飞行过程中的实时质量，g为重力加速度，θ为弹道倾角，X为气动阻力。

推力P和发动机有效喷气速度ue为：

(2)

式中：u为发动机燃气相对弹体的喷射速度，Sa为喷管截面积，pa为燃气静压，p为大气静压。

将式(2)代入式(1)，可得：

(3)

式(3)的两端关于时间τ进行积分可得：

(4)

当积分上限为tk时，即可求得导弹在关机点的速度Vk：

(5)

式中：Vu k为真空环境、不计重力条件下导弹主动段关机点的速度，ΔV1k为到关机点重力造成的速度损失，ΔV2k为到关机点气动阻力造成的速度损失，ΔV3k为到关机点大气压力造成的速度损失。

(6)

导弹飞行过程中质量与初始质量的比值μ=m/m0，则：

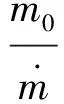
(7)

将式(7)代入式(5)，可得：

(8)

式中：Sm为最大横截面积，Cx为阻力系数，ρ为大气密度。

表1 各个变量的数量级(国际单位制)Table 1 The order of magnitude of the variable (International system of units)

由表1可知，Vu k的数量级为103，而ΔV1k数量级为102且接近103。在整个飞行过程中，同一高度下，相对密度ρ/ρ0与相对压强p/p0的数量级基本一致，可得：

(9)

除与ΔV3k数量级相同的积分项，ΔV2k的其余积分项CxV2变化范围为0～106，在积分区域的面积数量级为105，Sm与Sa数量级一致，而ΔV3k的常数项p0大小为101325，所以ΔV2k与ΔV3k数量级一致，二者近似相等。ΔV3k的常数项数量级为102，p/p0成指数下降趋势，积分项明显小于1，由此可知，Vu k>ΔV1k>ΔV3k≈ΔV2k。

3.1Vu k的估算

直接积分可得Vu k：

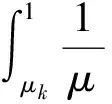
(10)

式(10)即为齐奥尔科夫斯基公式，用于计算导弹主动段关机点的理想速度。根据现有发动机工艺水平确定ue和μk，进而估算Vu k的大小。

3.2ΔV1k的估算

将重力加速度g近似为地面重力加速度g0，对sinθ进行积分即可得到ΔV1k的近似值。因为导弹在主动段以小攻角飞行，根据θ=φ-α，将弹道倾角近似为飞行程序角φ。导弹飞行程序分为垂直起飞段、程序转弯段、瞄准段三段，根据典型的弹道飞行程序，取θ(μ)为：

(11)

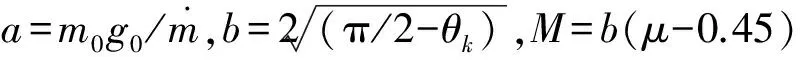
(12)

其中,θk<π/2且为定值，则积分下限随μ0增大而增大，满足0≤b(μ0-0.45)≤0.5b。被积表达式为超越方程，无法得到其积分表达式，需对三角函数级数展开，可得：

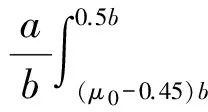
(13)

根据交错级数的收敛定理可知级数必然收敛，被积函数级数展开满足一致收敛性，当θk<π/2时，令μ0=0.45，利用式(13)计算可得：

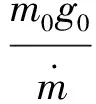
(14)

3.3ΔV2k的估算

根据Vu k和ΔV1k的估算公式，可得到主动段飞行过程中任意质量比μ下的理想速度Vu和重力造成的速度损失ΔV1。利用Vu和ΔV1近似表示飞行过程中的速度V，可得到导弹在发射坐标系下y轴的位移大小。根据图5所示，x轴位移远远小于地球半径，则tanβk≈sinβk，可利用位移y近似表示高度：

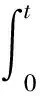
(15)

因为当地声速根据高度确定，计算得到h即可得到导弹飞行马赫数和当地空气密度。高度和速度是时间的函数，通过式(7)可知,高度和速度可看作是质量比μ的函数。根据高度和马赫数插值求出整个飞行过程中的气动阻力系数，通过拟合近似也可将阻力系数看作质量比的函数，即Cx(μ)。取步长Δμ，利用梯形积分公式即可得到ΔV2k：

(16)

3.4ΔV3k的估算

与估算ΔV2k的方法相似，将弹道倾角看作μ的函数，根据Vu k、ΔV1k和ΔV2k的估算值，近似表示飞行过程中的速度V，利用速度计算h：

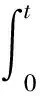
ΔV1(1-nΔμ)-ΔV2(1-nΔμ))sin(θ(1-nΔμ))

(17)

根据高度得到当地压强计算ΔV3k：

(18)

根据主动段关机点参数估算导弹全射程L的公式[12]，可利用计算得到的Vu k、ΔV1k、ΔV2k、ΔV3k和h估算全射程，即可实现利用导弹的有效喷气速度、最大横截面积、气动参数等易于估算的基本参数对减阻增程结果的定量分析。其中有效喷气速度、关机点质量比等参数由目前的工艺水平所确定，最大横截面积、气动系数等参数由导弹的外形所确定。

(19)

式中：R为地球半径,βk为主动段射程角,βc为被动段射程角,Θk为关机点速度倾角,υk为能量参数。

3.5射程的迭代计算

在对高度和ΔV2k进行计算时，只利用了部分速度损失值，忽略了ΔV2k、ΔV3k的影响，得到的计算结果将影响全射程的计算精度，同时直接影响因气动阻力造成的速度损失ΔV2k的计算结果，进而影响减阻增程的定量分析结果。

在得到Vu k、ΔV1k、ΔV2k、ΔV3k的基础上，将结果再次代入进行迭代计算，得到满足精度要求的射程计算结果。计算流程如图6所示。

4 仿真结果与分析

仿真计算未减阻构型和加装激波杆构型的气动阻力系数如图7～8所示。两种构型的气动阻力系数曲线在跨声速时变化剧烈，在Ma2～Ma25范围内曲线平滑。整个过程飞行的高度和马赫数随时间增加而单调递增，可以根据估算得到部分节点的高度和马赫数插值计算气动阻力系数，并利用拟合得到的气动阻力系数表达式计算ΔV2k。

拟合得到的气动阻力系数如图11所示，与其他拟合结果相比，分段二阶拟合效果最好，利用质量比分段二次函数表示阻力系数的公式为：

(20)

同理，分段拟合减阻构型阻力系数的效果如图12所示，得到的近似公式为：

(21)

最终计算得到减阻、未减阻构型在关机点的高度、速度和二者的射程如表2所示。对结果进行迭代计算，在射程误差满足小于0.01 km的条件下，减阻和未减阻构型的全射程计算分别迭代3和5次得到收敛值，二者精确的关机点状态量和射程如表2所示。通过迭代结果可以看到将ΔV2k、ΔV3k代入，对高度h、ΔV2k、ΔV3k进行再次计算能有效提高计算精度。

与迭代计算的结果相比，忽略ΔV2k、ΔV3k对高度的影响进行计算，即忽略了气动力、大气压力的影响，根据式(15)可知，计算得到的未减阻和减阻弹道关机点高度一致。二者相比，减阻构型使关机点速度增加52.53 m/s，全射程增加134.02 km。迭代计算结果显示，减阻构型使关机点的高度增加2.32 km，速度增加61.69 m/s，全射程增加162.36 km。计算结果的比较说明：迭代计算ΔV2k、ΔV3k进一步提高了主动段射程的计算精度，有利于减阻与未减阻弹道全射程的比较与分析。

表2 一次计算、迭代计算得到的关机点状态量和射程Table 2 State of the shutdown point and range by first calculation and iteration

未减阻构型和减阻构型各个速度迭代结果随质量比的变化如图14～15所示。在关机点因高度、气动阻力、压强导致速度减少量如表3所示，其中因高度增加而导致速度减小的量占速度减小总量ΔVs的75%左右，采用减阻构型使ΔV2k在ΔVs中的占比由原先的16.29%减小为11.46%。数据表明,ΔV1k= 800.5 m/s、ΔV2k变化范围为100 ～ 180 m/s、ΔV3k≈ 120 m/s，远小于速度V≈ 5800 m/s，验证了估算方法中各个速度数量级的推算结果，说明在对ΔV1k、ΔV2k、ΔV3k进行计算时，可以忽略量与量之间的耦合作用进行近似计算。

整个飞行过程中，两种构型的飞行速度差随质量比的变化曲线如图16所示。在飞行初始阶段，速度较低，气动阻力较小，二者速度差别不大，随着质量的减小，二者的气动阻力差变大，速度差也随之增加，但飞行到高空后，空气密度减小，二者的气动阻力急剧减小，速度差也随之减小。

表3 速度减少量Table 3 Speed reduction

计算出的关机点状态量和射程如表4所示，得到减阻和未减阻导弹的仿真弹道如图18所示。其中坐标原点为地心，发射点、目标点和地心所在平面截取地球得到的半圆为图中所示的地球表面。

表4 射程和关机点状态量计算结果比较Table 4 Comparison of the range and the state at shutdown point

与数值仿真计算结果相比，本文计算得到的关机点状态量、射程的偏差在数值仿真结果中所占百分比如表5所示，其中关机点高度的计算结果偏差较大，关机点的状态量中速度对全射程的影响更大，结果表明,本文方法能获得较高精度的关机点状态值和全射程量。

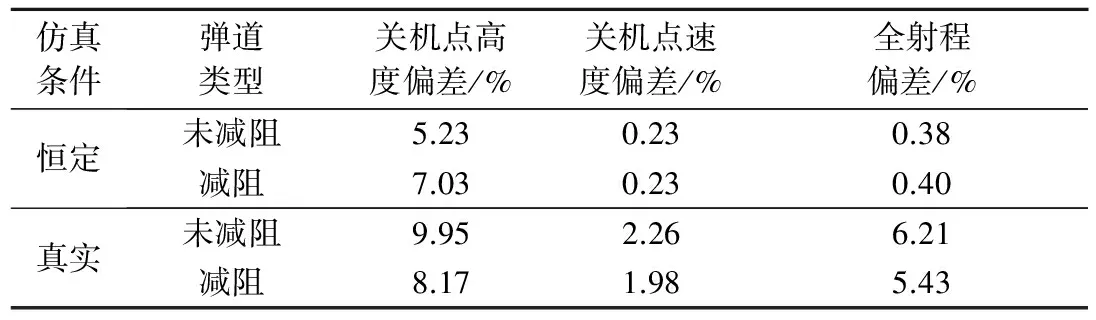
表5 射程和关机点状态量的计算偏差Table 5 Computing deviation of the range and the state at shutdown point

在相同的运行环境下，利用数值积分算法进行计算，当推力和秒耗量为恒定值时，数值积分需用时26.55 s，当推力和秒耗量为真实值时，增加了推力和秒耗量的差值计算，用时45.42 s。数值积分计算过程中，每经过一个时间步长，需计算当前时间下的推力和秒耗量，就需要进行一次插值计算，大大增加了计算量。在多次迭代计算的情况下，本文的方法只用了1.46 s，说明相比数值积分算法，本文的方法能以较高的计算速度获得较高精度的关机点状态和射程估算值。

5 结 论

1)提出适用于未减阻弹道和减阻设计弹道射程快速、高精度的计算方法。根据弹道导弹飞行过程中的速度计算公式，推导了基于导弹基本参数进行射程估算的计算公式，可在弹道设计过程中根据设计的基本参数论证导弹是否满足射程指标，为参数的优化提供依据，或根据现有工艺水平和具体外形估算外军导弹的最大射程。

2)利用函数拟合近似计算阻力系数。对原有的气动阻力系数表通过函数分段拟合的方法计算气动阻力，保证了因阻力造成的损失速度的计算精度，提高了计算速度。

3)建立ΔV2k和ΔV3k的迭代模型。将近似计算结果作为初值代入迭代模型进行计算，提高了关机点速度的计算精度。经过高度和气动系数的迭代计算能快速有效得到满足精度的计算结果。通过减阻设计，整个飞行过程关机点的速度增加61.69 m/s，导弹的射程增加了162.36 km，增程的效果明显。

[1] 鲜勇, 李少朋, 李振华, 等. 基于梯度粒子群算法的纵横向机动跳跃弹道设计及优化[J]. 弹道学报, 2015, 27(3):1-6. [Xian Yong, Li Shao-peng, Li Zhen-hua, et al. Design and optimization of vertical wavy and crosswise maneuvering trajectory based on grads particle swarm algorithm [J]. Journal of Ballistics, 2015, 27(3): 1-6.]

[2] 刘炳琪, 鲜勇, 李振华, 等. 基于非连续点火的变射面空间“M”形弹道设计及优化[J]. 固体火箭技术, 2015, 38(5):608-613. [Liu Bing-qi, Xian Yong, Li Zhen-hua, et al. Design and optimization of changeable launching plane ‘M’ maneuvering trajectory based on discontinuous ignition [J]. Journal of Solid Rocket Technology, 2015, 38(5): 608-613.]

[3] Gauer M, Paull A. Numerical investigation of a spiked blunt nose cone at hypersonic speeds [J]. Journal of Spacecraft and Rockets, 2008, 45 (3): 459-471.

[4] 封贝贝, 陈大融, 汪家道, 等. 头部形状对超声速飞行器力学性能影响分析[J]. 飞行力学, 2012, 30(6):537-540. [Feng Bei-bei, Chen Da-rong, Wang Jia-dao, et al. Affect of head shape on flight dynamics of supersonic vehicles [J]. Flight Dynamics, 2012, 30(6): 537-540.]

[5] Mansour K, Khorsandi M. The drag reduction in spherical spiked blunt body [J]. Acta Astronautica, 2014, 99: 92-98.

[6] Tahani M, Karimi M S, Motlagh A M, et al. Numerical investigation of drag and heat reduction in hypersonic spiked blunt bodies [J]. Heat and Mass Transfer, 2013, 49 (10): 1369-1384.

[7] 李永红, 高川, 唐新武. 激波针气动特性及外形参数优化研究[J]. 兵工学报, 2016, 37(8):1415-1420. [Li Yong-hong, Gao Chuan, Tang Xin-wu. Drag reduction characteristics and design optimization of spikes [J]. Acta Armamentarii, 2016, 37(8): 1415 -1420.]

[8] 王海峰, 赵久奋, 王伟. 面向任务级弹道导弹的通用弹道设计仿真研究[J]. 计算机仿真, 2016, 33(6):64-68. [Wang Hai-feng, Zhao Jiu-fen, Wang Wei. Research on general trajectory design and simulation for mission level ballistic missile [J]. Computer Simulation, 2016, 33(6): 64-68.]

[9] 张涛, 安玮, 周一宇. 基于推力加速度模板的主动段弹道跟踪方法[J]. 宇航学报, 2006, 27(3):385-389. [Zhang Tao, An Wei, Zhou Yi-yu. The trajectory tracking method in boost phase using thrust acceleration profile [J]. Journal of Astronautics, 2006, 27(3): 385-389.]

[10] 王洁瑶, 江涌, 钟世勇, 等. 高超声速远程导弹弹道解析估算与特性分析[J]. 宇航学报，2016, 37(4):403-410. [Wang Jie-yao, Jiang Yong, Zhong Shi-yong, et al. Analytical estimation and analysis of trajectory performance for hypersonic long-range missiles [J]. Journal of Astronautics, 2016, 37(4): 403-410.]

[11] 王洁瑶, 江涌, 钟世勇. 助推-滑翔弹道高精度滑翔射程解析估算方法[J]. 宇航学报, 2016, 37(5): 519-525. [Wang Jie-yao, Jiang Yong, Zhong Shi-yong. A high accuracy analytical estimation method for glide range of the boost-glide trajectories [J]. Journal of Astronautics, 2016, 37(5): 519-525.]

[12] 张毅, 肖龙旭, 王顺宏. 弹道导弹弹道学[M]. 长沙:国防科技大学出版社,2005:183-189.

RangeEstimationandAnalysisforExtendedTrajectoryBasedonDragReductionDesign

LING Wang-hui, XIAN Yong, GUO Wei-lin, LI Jie, ZHANG Da-qiao

(7th Department, Rocket Force University of Engineering, Xi’an 710025, China)

In order to realize the quantitative analysis of the trajectory and the evaluation of the extend range by using the drag reduction design, a fast and accurate estimation method is proposed based on the basic parameters of a missile. By establishing a drag reduction model, an aerodynamic drag coefficient table is calculated. Then the speed calculation formula is integrated item by item. The initial value of the state at the shutdown point and the range are obtained by the height approximation and the fitting aerodynamic coefficient. After the iteration, the result satisfies the accuracy requirements of the range. The simulation results show that the heuristic calculation of the height and the aerodynamic coefficients can effectively and quickly get the satisfying results. Under the drag reduction design, the final missile range is increased by 162.36 km and the extended-range effect is obvious.

Drag reduction design; Trajectory extension; Range rapid estimation; Aerodynamic coefficient fit; Iteration

TP 731

A

1000-1328(2017)10- 1048- 09

10.3873/j.issn.1000-1328.2017.10.005

2017- 05- 24;

2017- 07- 19

凌王辉(1992-)，男，硕士生，主要从事飞行器设计、制导方面的研究。

通信地址:陕西省西安市灞桥区同心路2号(710025)

电话:15399420435

E-mail:ling_wanghui@163.com