电动汽车某连接器弹片式接触端子的优化设计

欧阳波仪

(湖南汽车工程职业学院，湖南株洲 412001)

电动汽车某连接器弹片式接触端子的优化设计

欧阳波仪

(湖南汽车工程职业学院，湖南株洲 412001)

以弹片式接触端子装配时的插入力、拔出力和应力为质量特性，以端子使用后不会产生永久变形为目标，利用响应曲面法与有限元分析法完成优化设计，利用统计软件 Minitab以线性回归方法建构模型，验证了采用响应曲面法建立的回归模型具有良好的预测性。

弹片式接触端子；优化设计；有限元分析

0 引言

电子连接器是电动汽车上非常关键的器件之一，其公端圆柱端子和母端弹片端子装配(如图1所示)，在接触界面上产生正向接触力，从而达到传输电流或信号的目的。正向接触力是由母端弹片端子提供，为提高传输性能，希望正向接触力越大。然而，正向接触力增大会使得插拔力增大，而使得操作难度增加、连接器寿命降低。因此，连接器端子设计要满足低插拔力、足够正向接触力的要求。行业内常以“经验+试验”确定弹片式接触端子的力臂、宽度等几何参数，虽然能满足要求，但需要经过反复试验修正，设计效率不高。

图1 电子连接器工作原理示意图

对此，作者以图1中弹片式接触端子为研究对象，利用实验设计法(Design of Experiments，DOE)和有限元分析设计法，对母端弹片端子几何参数进行优化设计，使其满足低插拔力、足够正向接触力的要求。

1 相关理论分析

1.1 正向接触力与插入力分析

将弹片式接触端子的公端视为刚体，插入过程中的每个瞬间，插入力与接触力呈静力平衡，可以用库仑摩擦定律计算[1]。如图2所示，由于摩擦力的关系，接触力的方向为正向角ψ加上偏移摩擦角α，在接触点上有两个力，一个是正向力Fn以及与其垂直的切线方向力Ft，而两个力之间的关系为Ft=μFn(μ为摩擦因数)，两个力的合力F在y方向的分力可以用式(1)表示：

Fy=Fnsinψ+Ftcosψ=Fnsinψ+μFncosψ

(1)

Fy为接触点上所需要的插入力，在x方向力F的分力可以用式(2)表示：

Fx=Fncosψ-Ftsinψ=Fn(cosψ-μsinψ)

(2)

插入过程中，开始作用点是公端圆柱端子的前端导圆角，接触到母端弹片端子，就会有力产生，当接触角变成0°，作用力趋于平缓不再有变化。

图2 插入力分析

1.2 响应曲面法的应用分析

响应曲面法是广泛运用于工程问题的一种优化统计方法，能够有效地利用实验设计规划所获得的实验数据，以回归方法表示质量因子的参数，再以技术优化达到质量优化的结果[2]。响应曲面法不但可回归实验结果，更能够判别实验中各因子的效果，甚至是复杂的因子间交叉效应，通过统计的检定、残差的分析，还可检验实验的精准度与可信度。

2 有限元分析实验设计

采用性价比较高的磷青铜(C521)为接触端子的材料[3]，其弹性模量为110 kN/mm2、泊松比为0.34、屈服强度为593 N/mm2。此连接器间距为10 mm×10 mm，受空间限制，采用厚度为1 mm的板材。

2.1 模型设计

如图3所示，利用Pro/E建立连接器弹片式接触端子的3D模型，转为STEP格式提供给ABAQUS软件进行有限元分析，采用ABAQUS/Standard 的二次四面体元素(C3D10M)网格。以连接器弹片式接触端子的几何参数为分析要素，以实验设计方法规划有限元分析方案，利用反应曲面方法将模拟方案的分析结果构建反应曲面模型，以探讨公端圆柱端子的插入力与拔出力，进而完成优化设计。

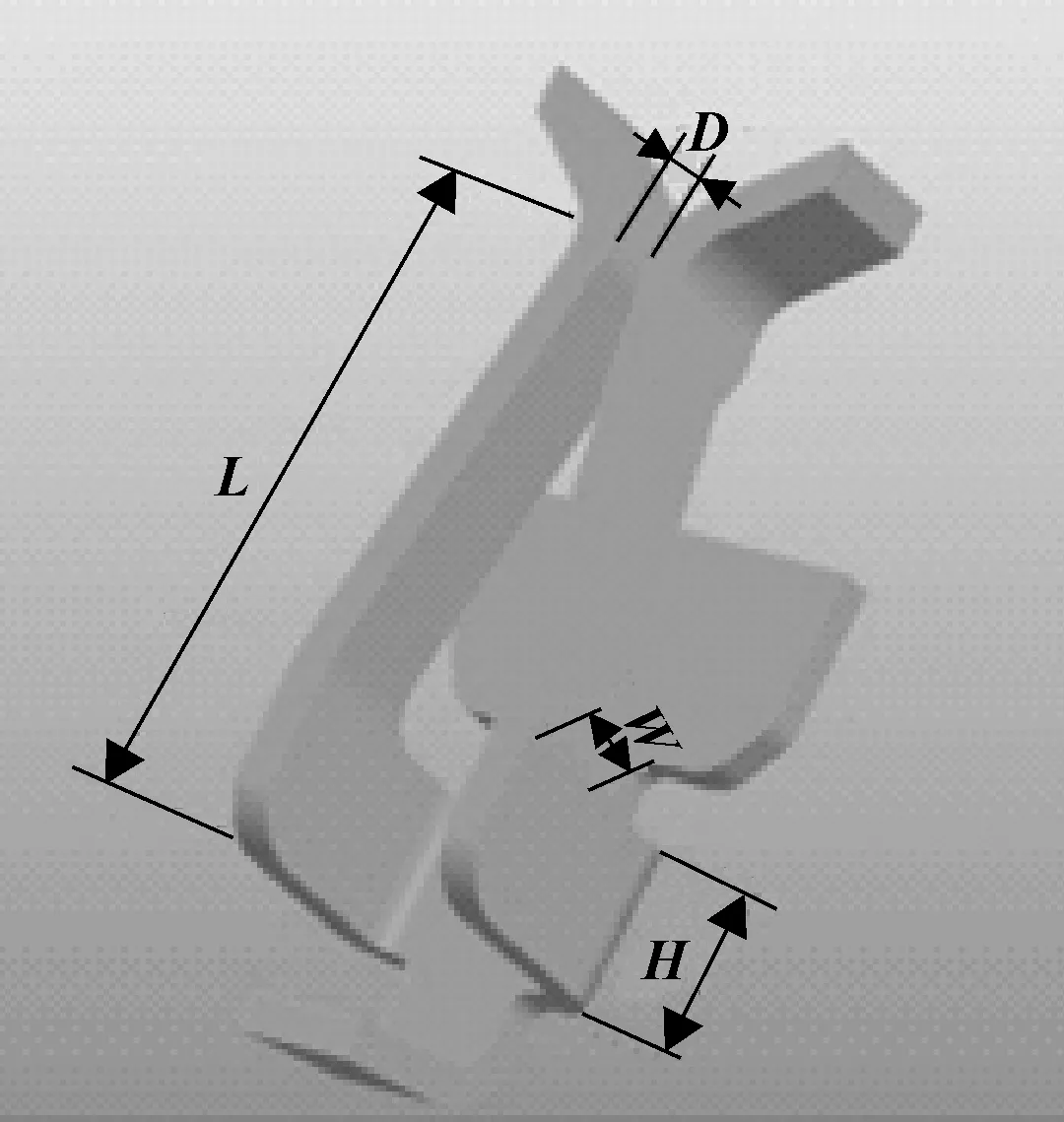
图3 几何设计参数

2.2 边界与网格设定

如图4所示，母端两侧与塑料端子座采取限位处理，没有任何轴向的自由度运动；公端圆柱端子会沿着负Y轴方向作插入动作和拔出动作，因此设定公端圆柱端子的位移为1 mm，其余均为0。将母端有限元模型的网格数量设置为介于0.5×104～9.5×104之间，并以每1万个元素网格为增量，观察网格数量和插入力及拔出力计值结果的关系，选择适当的元素网格数量进行分析。由于当网格数量7万以上时，有限元分析的插入力与拔出力可收敛至一稳定值，故文中后续仿真分析的有限元模型皆采用7万个网格元素来建立。

图4 CAE模型及边界条件

2.3 实验设计

为确定母端端子满足预设插入力及拔出力的质量特性要求，如图3所示，选择弹片力臂长L、弹片根部高度H、弹片力臂切口宽度W以及弹片式接触端子接触区间隙D为质量因子，其他的几何相关参数均为固定数值不变动。

采用响应曲面实验设计进行仿真实验，每个质量因子的实验设计皆采用三水平，分别以编码变量-1、0、1代表。每个质量因子的自然变量水平与编码变量水平的关系如表1所示。依照响应曲面四因子三水平设计，设计表2所示的25组实验。

表1可控制因子及水平表

mm

表2 Box-Behnken 的四因子实验设计

3 试验结果分析

3.1 结构安全分析

为了验证所设定的边界条件是否合理，以现有端子实测数据与有限元分析数据进行对比测试，如表3所示，发现两者数据趋近，表明有限元分析值是可参考的。

表3 现有端子实测值与现有端子有限元分析数值 N

依据响应曲面实验设计规划表2中实验点，由ABAQUS有限元软件分析，得到图5所示的应力分布图。将每一实验点的最大插入力、最大拔出力以及母端子的最大应力值进行优化处理，得到表4所示的模拟点与结果。对表中28组重复角点实验点的等效应力进行分析，都没有超出材料屈服强度，即公端圆柱端子插入与拔出的过程中不会产生永久变形，可视为安全设计。

图5 应力分布图

序号弹片力臂长L/mm弹片根部高度H/mm切口宽度W/mm接触区间隙D/mm插入力/N拔出力/N应力/(N·mm-2)11.550.300.3250.130.1400.053485.421.550.400.3250.130.1890.072533.931.350.300.3250.130.2050.077586.041.350.400.3250.130.2870.108586.051.550.350.3000.130.1580.060470.261.550.350.3500.130.1720.065559.371.350.350.3000.130.2340.088586.081.350.350.3500.130.2550.096586.091.550.350.3250.180.1000.044384.0101.550.350.3250.080.2400.081586.0111.350.350.3250.180.1490.065537.2121.350.350.3250.080.3510.115586.0131.450.300.3000.130.1610.061528.8141.450.300.3500.130.1770.067581.2151.450.400.3000.130.2160.082586.0161.450.400.3500.130.2370.090586.0171.450.300.3250.180.1000.044356.8181.450.300.3250.080.2420.081586.0191.450.400.3250.180.1380.061433.0201.450.400.3250.080.3310.110586.0211.450.350.3000.180.1140.050374.4221.450.350.3000.080.2720.091586.1231.450.350.3500.180.1240.054400.4241.450.350.3500.080.2980.099586.1251.450.350.3250.130.1950.074545.5261.450.350.3250.130.1950.074545.5271.450.350.3250.130.1950.074545.5281.450.350.3250.130.1950.074545.5

3.2 模型回归与实验

采用 Minitab 统计软件进行实验样本回归分析，实验数据见表4，回归模型采用二阶多项式标准模型：

(3)

其中：y代表因变量；x代表自变量；β代表模型系数；ε代表模型残差，可利用实验数据以回归方法决定。回归采用的因子水平系以自然变量值表示。

回归模型的显著性可以用其F统计量判定，数值越大，代表模型越显著。回归模型的变异解释能力可以用其判定系数R2判定，越接近1代表对变异的解释能力越强:然而，复杂度高的模型会有高估变异能力的倾向，因此修正为利用调整判定系数R2判定。

回归自由度为14、残差自由度为13，在信心水平为95%的条件下，分析得到插入力、拔出力和应力预测值的残差常态概率分别如图6所示，可以看出没有明显偏离，证实该方法的可行性。

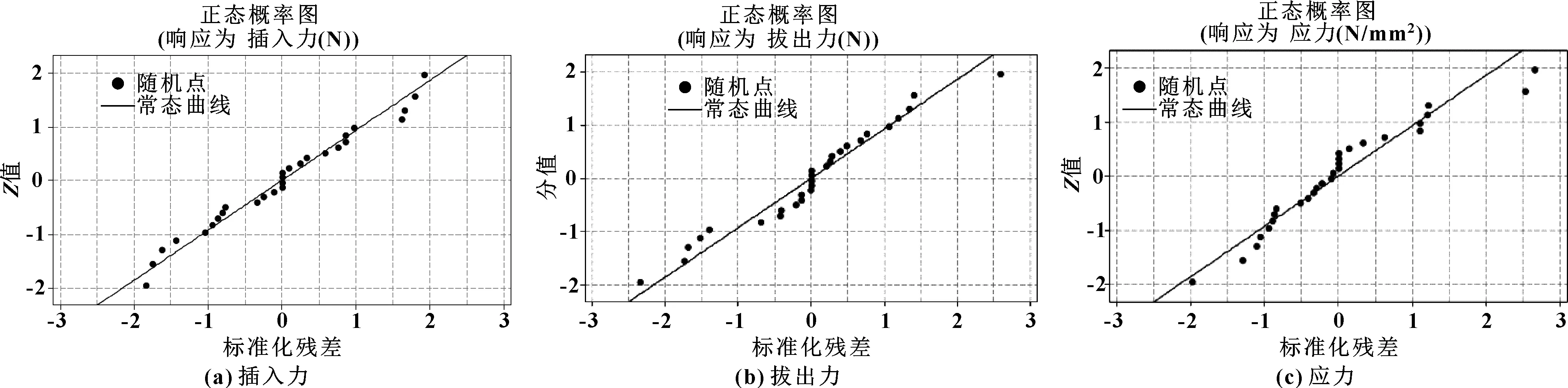
图6 插入力、拔出力和应力预测值的残差常态概率图

3.3 优化设计与验证

端子材料磷青铜的屈服强度为593 N/mm2，并且根据需求，设计插入力及最小拔出力分别为0.263 N及0.079 N。采用统计软件Minitab求解，所得到的优化参数(即质量因子)如表5所示。

表5 优化设计参数(即质量因子) mm

利用Minitab分析得到如图7所示的有限元分析等效应力图，可以看出能够达到端子使用后不会产生永久变形的目标。

图7 最佳化几何组合有限元分析结果

进一步以有限元分析结果为参照，插入力、拔出力及应力等质量特性的统计值误差都小于±2%，验证了采用响应曲面法建立模型具有良好的预测性。因此，应用文中方法分析其他类似弹片式接触端子的结构设计，可为工程设计上的参考。

4 小结

通过响应曲面实验设计进行仿真实验，采用 Minitab 统计软件进行回归分析，从插入力、拔出力和应力预测值的残差常态概率可以看出没有明显偏离，说明这一方法是可行性的。在此基础上，设计插入力及最小拔出力分别为0.263 N及0.079 N，采用统计软件Minitab求解，得出L=1.38 mm、H=0.37 mm、W=0.32 mm、D=0.15 mm，以有限元分析结果为参照，验证了采用响应曲面法建立模型具有良好的预测性，可为工程设计上的参考。

[1]赵经东.刚性接触悬挂铜铝接线端子断裂分析[J].城市轨道交通研究,2012,15(11):111-113,116.

ZHAO J D.Analysis of Fractures on Copper and Aluminum Connector in Rigid Overhead Catenary System[J].Urban Mass Transit,2012,15(11):111-113,116.

[2]徐卫国.基于响应曲面法的波形弹簧片冲压工艺参数优化[J].锻压技术,2017(3):175-179.

XU W G.Optimization on Stamping Parameters of Wave Spring Sheet Based on Response Surface Method[J].Forging & Stamping Technology,2017(3):175-179.

[3]欧阳金栋.磷青铜薄板的微塑性成形尺度效应研究[D].南京:南京航空航天大学,2015.

OptimizationDesignofShrapnelContactTerminalforConnectorofElectricVehicle

OUYANG Boyi

(Hunan Automotive Engineering Vocational College，Zhuzhou Hunan 412001，China)

Taking the assembly insertion force, pull out force and stress as quality characteristics, taking the terminal not produce permanent deformation as the goal,the response surface method and the finite element analysis were used to make optimization design of the long arm of the shrapnel contact terminal, the mathematic model was built with linear regression method based on Minitab statistical software.The results verify that the regression model built with response surface method has good prediction performance.

Shrapnel contact terminal; Optimization design; Finite element analysis

2017-06-07

湖南省教育厅科学研究项目(16C0820)

欧阳波仪(1978—)，男，硕士，副教授，从事模具设计制造教学与研究。E-mail：oyby721@163.com。

10.19466/j.cnki.1674-1986.2017.10.011

U469.72

A

1674-1986(2017)10-047-04