最小二乘法拟合热电阻测温结果的准确性分析

李晓麟

最小二乘法拟合热电阻测温结果的准确性分析

李晓麟

（甘肃省计量研究院，甘肃 兰州 730070）

工业上已经对铂、铜等金属热电阻进行电阻和温度特性的研究。针对工业上对提高热电阻测温准确性的测量方法，本文采用最小二乘法对数据进行处理，总结出一种测电阻和温度关系的转化公式和精度表。然后，比对其他方法测出的数据得出，本方法可以提高温度传感器对温度测量的准确性。

温度测量；热电阻；最小二乘法；准确性

在工业生产和生活中，温度是一个很重要的测量物理量，若要精确测量还需要克服一些问题。就目前应用比较多的温度传感器而言，主要包括4种：热电偶、热电阻、热敏电阻和集成温度传感器。热电阻温度传感器作为比较广泛应用的测温元件之一，具有互换性好、耐腐蚀、性能稳定以及使用方便等特点［1］。工业上的做法经常是将热电阻接到电桥的电桥臂上，通过测量，电桥两端输出的不同的电流，转化为温度的不同值，从而知晓测得的温度。在实际使用过程中，大多数是按照厂商提供的温度标准值，如果需要测量精度高的温度，就需要与计量机构出具的证书对比修正，或者按照规程上的要求进行系数校正［2］。当然，测量的时候有时只能对有限的温度测量范围进行修改校正，没有被修正的测量温度点就会产生较大的测量误差。工业上的常规方法是由于铂电阻的非线性以及电桥臂的测量温度不平衡带来了一定的测量误差，通常把铂电阻放在测温的现场，减小测温点到测量变换电路之间的距离，这样就会减小产生的自身引线电阻［3］。本文以pt100铂电阻传感器为例，通过测量更宽的测量温度点，对数据进行最小二乘法分析校正，得出最小误差的测量温度值，从而提高精度。

1 测量热电阻的原理以及进行温度测量的误差

金属铂具有一种固有特性，即电阻值随温度的增加而增加，我们可利用这一特点来测量温度。在某一特定温度下，通过测量铂电阻的电阻，然后通过计算公式得到需要的温度值。科研工作者和工程师们按照国际统一的标准来制造很多具有代表性的工艺产品，然后进行各方面的测试，并对所得的数据进行分析处理，得到相应的曲线图，总结得到一个具有普遍性意义的公式（即电阻与温度特性的公式）：

式中，RT代表温度为T时铂电阻的电阻值，R0代表温度为0时的铂电阻的电阻值，A、B、C代表常数。

由JJG229-2011《工业铂铜热电阻检测规定》可知，铂电阻的检测温度范围为0～100℃，通过国家规定的标准来检测合格的铂电阻传感器的测量温度的检定点，由查分度表得到。其中分度表是理想情况下纯铂的电阻与温度的关系表。当式（1）（2）中R0=100.000 0，A=3.908 4×10-3，B=-5.775 44×10-7，C=-4.183 45×10-12时，其电阻和温度的关系可以用分度表来表示。但是，在工业生产过程中，厂家生产出来的铂电阻的电阻-温度特性关系与分度表上有一定的偏差，这是由以下几点原因造成的：①铂丝的纯度；②铂敏感元器件绝缘；③材料热膨胀和电泄露。

2 提高热电阻测温精度和减小误差的方法

铂电阻是一种典型的热电阻温度传感器，直接用它比对分度表来测量温度，这样的方法会产生较大的测量误差，即使是准确度最高的铂电阻（AA级）也会有0.1左右的测量温度偏差，尤其是对一些精密温度测量时有非常大的影响。分析铂电阻的电阻与温度的特性公式得出，要测定公式中的系数，对于温度大于0的时候要测量三点；对于温度低于0的时候要测量4个点。令0℃附近的点为T1、下限温度为T2和上限温度为T3，测得实际的电阻值为R1、R2、R3,得出以下公式［4］：

从而求出未知数R0，A和B，这样对测量点测量时可以得到准确的温度数据。

3 以最小二乘法进行拟合

使用最小二乘法求拟合曲线，不同的数学模型模拟出来的函数不一样，当要拟合的函数为多项式时，假设给定的一组数据( )xiyj，i,j=1,2,…,N求P（P＜N）次多项式

即有方程组：

利用此方程证明有唯一的解，这个方程适合一般的数据拟合，但此方程存在一定的缺点，当P足够大的时候，此方程就失效了。

在温度大于0的电阻和温度特性的公式中，只需要测量3个温度点（比如温度为0附近时的某温度点T1、温度可以达到的上限点T2、温度可以达到的下限点T3），再加上这3个点所处位置的电阻值R1、R2、R3，就可以得到R0、A、B的值（通过最小二乘法计算得到）。其中里面的系数由以下方程组得到：

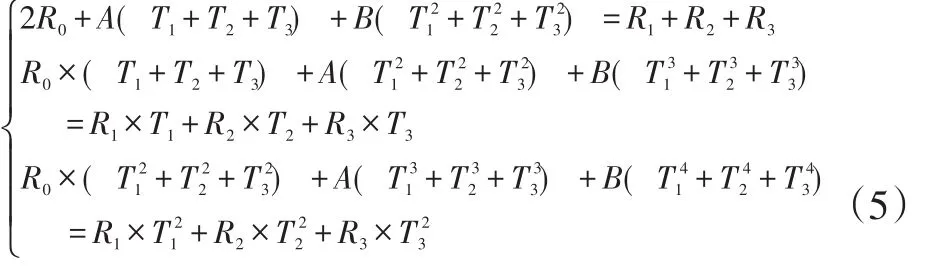
再由上式得到的系数值算出被测铂电阻的分度表。

4 验证最小二乘法拟合数据的准确性

在求近似函数的所有数值方法中，有一种叫做函数逼近，即曲线拟合。曲线拟合只是要求给定的数据点在某种程度上逼近或者某种意义上讲是一种基本的趋势，但不要求拟合的数据在每一个节点上与函数值一模一样。我们经常会选择合理的数值方法对数据进行筛选和处理，数据拟合受到大多数人的青睐。考虑到误差，进行曲线拟合处理数据时，往往很难选取合适的函数来拟合这些曲线，于是就产生了最小二乘法。

与传统方法比较来验证最小二乘法的正确性和可靠性，用工业上的铂电阻来测试，测量数据见表1。

表1 铂电阻测量数据结果

5 结语

本文通过最小二乘法原理，利用一些基本公式求出铂电阻中电阻与温度特性里面的一些参数，得出的数据与分度表进行比较，来确定是否准确。在实际生产生活中，使用新函数拟合出来的测量温度的数据比之前的要准确很多，也可以用来提高热电阻的准确度。

［1］国防科工委科技与质量司.热学计量［M］.北京：原子能出版社，2002.

［2］国家质量监督检验检疫总局.JJG229-2010工业铂铜热电阻检定规程［S］．北京：中国质检出版社，2010.

［3］国防科工委科技与质量司.计量技术基础［M］.北京：原子能出版社，2002.

［4］王能超.计算方法［M］.武汉：华中科技大学出版社，2010.

Accuracy Analysis of Measuring Thermal Resistance Temperature by Least Square Method

Li Xiaolin
（Gansu Institute of Metrology，Lanzhou Gansu 730070）

The resistance and temperature characteristics of platinum,copper and other metal thermal resistors have been studied in industry.In order to improve the accuracy of temperature measurement by thermal resistance in industry,this paperused the least square method to process the data and sum up a transformation formula and an accuracy table for measuring the resistance and temperature.Then,compared with other methods,this method can improve the accuracy of temperature measurement by the temperature sensor.

temperature measurement；thermal resistance；least square method；accuracy

TH811

A

1003-5168（2017）09-0053-02

2017-08-02

李晓麟（1988-），男，硕士，工程师，研究方向：热工计量。