射流清管器等效压降系数模型的建立及分析验证＊

陈建恒 何利民 罗小明 李清平

（1．中国石油大学（华东）油气储运安全省级重点实验室 山东青岛 266580； 2．中海油研究总院 北京 100028）

射流清管器等效压降系数模型的建立及分析验证＊

陈建恒1何利民1罗小明1李清平2

（1．中国石油大学（华东）油气储运安全省级重点实验室 山东青岛 266580； 2．中海油研究总院 北京 100028）

通过对射流清管过程进行动量和能量平衡分析，建立了等效压降系数计算模型，并利用CFD软件模拟计算了相同运行工况下的等效压降系数，分析验证了等效压降系数与清管器旁通率和气体雷诺数之间的内在关系。研究表明，射流清管器等效压降系数随旁通率的增加呈现微弱减小而后快速增长的趋势，同一旁通率下等效压降系数几乎不随射流气体雷诺数变化而变化；射流清管器结构中的突扩部分对旁通压降的贡献最大，比重接近70%。本文方法计算结果与CFD模拟结果的偏差在6．4%以内，吻合度较高，表明应用本文建立的模型可以较好地计算射流清管器等效压降系数，以此作为射流清管器动态模拟的重要输入参数。本文研究成果对优化射流清管器的设计及对射流清管器模型的修正具有重要的意义。

射流清管器；等效压降系数；计算模型；CFD模拟验证；旁通率；雷诺数

清管是管道流动安全保障的重要措施，是管道维护和运行中不可缺少的环节。对于输气管道的清管操作，由于驱动介质为运行速度较快的气体，因而清管器速度普遍较高，清管效果较差，因此对于气体管道清管器设计中速度控制显得尤其重要［1－7］。传统清管器在天然气凝析液管道中进行清管作业时，由于主体前后密闭，使清管器两端驱动压差大，运行速度快，易导致管道内涂层破坏、清管器运行不稳定、清管段塞超过下游接收设备的处理能力，给生产带来了很大的不确定性。

理想的清管速度不宜过快，当清管器的运行速度低于5 m／s时，清管的效率较高［7］。射流清管器是专门应用于气体管线的新型清管工具，通过在清管器主体中部开设一个旁通射流孔，使后方气体通过旁通孔进入清管器前方，有效地降低清管器驱动压差，进而减小清管器的运行速度，同时增强气体对下游积液的吹扫和剪切携带作用，有利于平缓清管段塞，给生产带来了显著的效益［2，8－13］。

压降系数是支配射流清管器驱动压差的重要参数，其可将清管器的驱动压差和清管器速度以及驱动气速相关联，从而求解清管器的运动规律，对于射流清管模型的准确建立具有重要的意义。Henkes等［14－15］对清管器前方有折流板的压降系数进行了研究，认为其与清管器结构具有重要的关系。然而，射流清管器的结构形式多样，需要深入分析结构参数的影响，阐明不同结构对压降的贡献。此外，影响压降的因素还可能包括流体自身的流动特征参数，探讨这些因素对射流清管压降系数的影响，对于分析压降、优化清管器设计以及修正射流清管模型具有重要的意义。

1 等效压降系数模型的建立

1．1 压降系数概念的建立

首先对射流清管过程进行受力分析，建立压降系数的概念。由于射流气体通过旁通孔从清管器后方进入前方，对前方积液进行吹扫和携带，使之分布到更长的管段上，因而前方堆积量大大降低，甚至无积液堆积，故模型的建立忽略清管器前方积液的存在，考虑单气相的影响。图1为简化的射流清管器在水平管内运动受力示意图。

对射流清管器运动过程进行动量分析，可得支配清管器的运动方程为

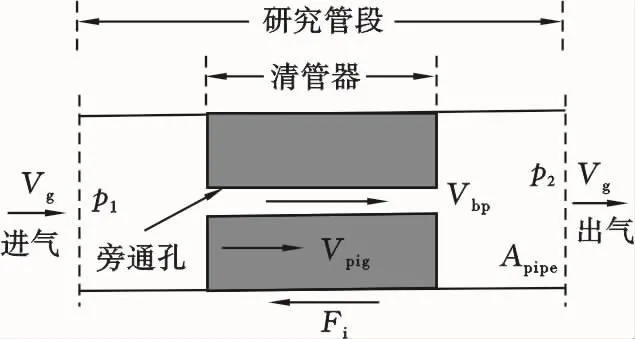
图1 射流清管器在水平管内运动受力分析Fig．1 The force analysis of bypass pig in a horizontol pipe

式（1）中：m、Vpig、Apipe分别为清管器质量、清管器速度、管道的横截面积；Δp为清管器前后的驱动压差；Fi为作用于清管器上的阻力。

将驱动压差Δp与旁通孔的气体流速Vbp进行关联，定义压降系数K，即

式（2）中：K 为压降系数，包含了突缩结构、突扩结构以及气体旁通孔内的摩擦造成的压降；ρ为气体密度；Vbp为清管器旁通孔中的平均气速，与后方驱动气速、清管器速度以及清管器旁通孔的大小有关，利用连续性方程进行计算［3］可得

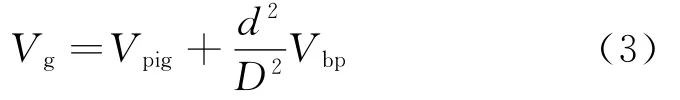
式（3）中：Vg为清管器后方的驱动气速（由于射流清管器的速度介于气速和液体速度之间［3］，从而清管器后方一段距离内将出现干气区，无液相存在，故驱动介质为气体）；d、D分别为旁通孔和管道的内径。

从式（2）、（3）可知，利用压降系数K 可将射流清管器的前后压差与驱动气速、清管器速度相关联，再结合式（1）便可描述清管器的运动。通过对射流清管器的运动过程受力分析可知，支配射流清管器的运动因素包括由清管器前后驱动压差形成的驱动力以及由摩擦力和重力等组成的运行阻力，驱动力和运动阻力在清管过程中的变化造成了清管器速度的波动性。对于一个特定密封结构的射流清管器而言，清管器与管壁间摩擦力的波动范围是确定的，则清管器的运动主要取决于前后驱动压差，因而若能寻求驱动压差与驱动气速以及清管器速度之间的关系，便可以实现射流清管器运行速度的求解。在这一关联求解的过程中，射流清管器压降系数的作用得到了体现，其可将驱动压差与旁通气速进行关联，进而得到清管器的驱动力与后方气速以及清管器速度的内在联系，因此射流清管模型的准确求解很大程度上取决于压降系数的计算。

1．2 等效压降系数模型的建立

本次研究立足于实际工程中具有广泛应用的射流清管器结构，如图2所示，清管器射流通道由2个不同的直管段d1和d2以及由d1向d2过渡的渐缩段组成。

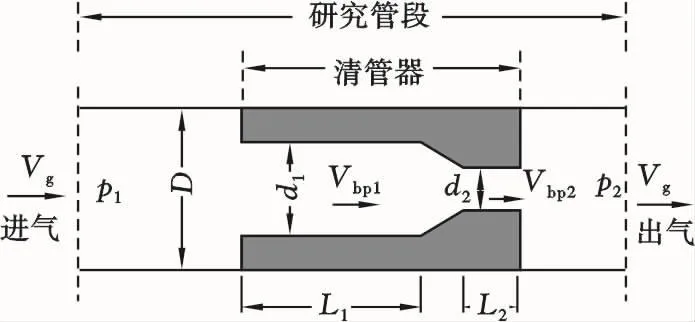
图2 射流清管器等效压降系数模型Fig．2 Model of bypass pig equivalent pressure drop coefficient

定义气体由上游管道D段历经突缩结构到达清管器的d1段对应的突缩压降系数为K1，由d2段历经突扩结构到达下游管道D段的突扩压降系数为K2。考虑清管器内部渐缩段的能量损失以及流体在射流通道内的摩阻损失，通过能量平衡分析，则可得到气体经过射流通道的总能量损失（即总压损失）为

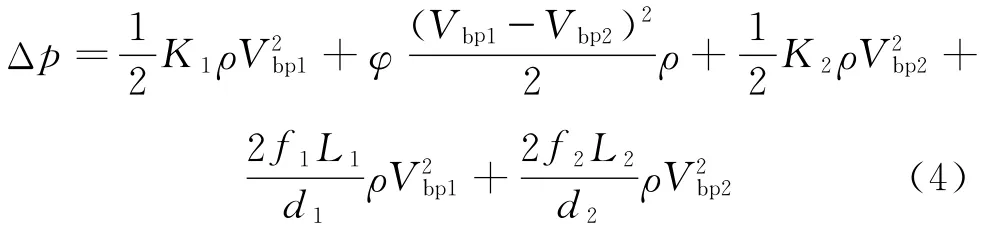
式（4）中：右端前3项分别为对应突缩、渐缩管段，突扩结构的压力损失，后2项为2个射流段内的摩阻损失；Vbp1、Vbp2分别对应清管器内d1、d2段的平均气速；ρ为气体的密度，实际工程应用中射流清管器内气体马赫数较小［6］，气体作为不可压处理；φ为气体经过渐缩部分的能量损失系数，与渐缩角θ有关，可由实验曲线确定［16］（在本次研究中，设计θ＝60°，取φ＝0．1，该取值与 CFD验证结果吻合）；f1、f2分别为2个射流通道内的范宁摩擦系数，与雷诺数和粗糙度有关，可采用Churchill关联式［17］计算。

为了能够将清管器前后的压降Δp与射流气速Vhp之间建立一个较为简单的关联公式，便于清管器模型的建立与求解，本次研究建立“等效压降系数”的概念，将射流通道d2段的射流气速Vbp2所对应的压降系数作为整个射流通道结构的等效压降系数Keq2，即

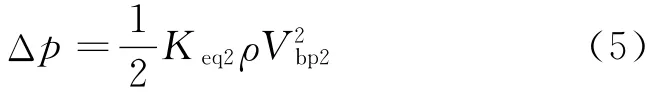
连续性方程为

式（6）中：A1、A2分别为两段射流通道的横截面积。

通过式（4）～（6）可得

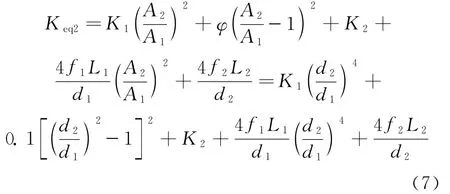
突缩压降系数K1可利用Idelchik公式［18］计算，突扩压降系数K2可由包达公式［19］计算，即

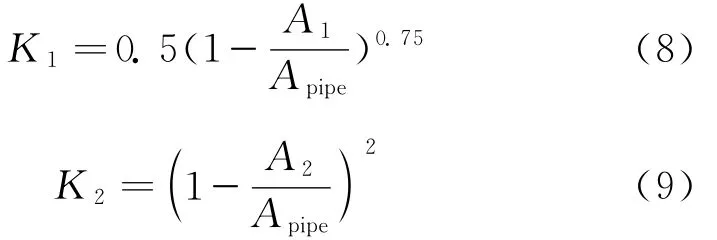
式（8）、（9）中：Apipe为管道的横截面积。

式（7）为本次研究建立的等效压降系数计算式。该计算模型的意义在于：通过等效压降系数将射流清管器前后复杂的压降损失计算式（4）转化成以Vbp2为基准的简单计算式（5），极大地方便了内部射流结构多变的射流清管模型的建立。

2 分析验证

从以上推导过程可以看出，射流清管器的等效压降系数是管道的结构参数和摩擦系数μ的函数，而摩擦系数又取决于气体的雷诺数。这里利用式（7）研究等效压降系数随射流气体雷诺数和射流清管器内部结构参数的变化，并利用CFD模拟软件FLUENT进行模型的对比验证。

2．1 几何模型

图3为本次研究采用的射流清管CFD模拟结构。为了能更加真实地模拟流动过程，采用三维结构对整个流域进行结构化六面体网格离散。

图3 射流清管模型网格划分Fig．3 Mesh dividing result of bypass pig

为了能够更细致地研究清管器周围的流场分布规律，模拟射流清管动态过程，以清管器为参考系，即将清管器看成不动，管道以清管器的速度向反方向运动。这种相对坐标设置的意义表现在：清管器匀速运动，驱动压差与清管器阻力相平衡，即清管器的合外力为零。为了使清管器前方长度达到充分发展状态，取前方的管道长度为30 D。清管器后方的长度也应该是充分发展的状态，但为了节省计算资源，速度入口采用UDF的方法进行定义，使得入口段长度减少为5 D即可满足要求。

2．2 数值模型与边界条件

在求解方法的选择上，求解模型采用Realizable k－ε模型，壁面条件采用Standard wall函数。这是因为，Singh等［15］将该湍流模型与壁面函数的模拟结果与实验数据进行对比，验证了求解模型和壁面函数选择对于射流效果的有效性；而对流项采用三阶QUICK离散格式，保证了结果高精度。

边界条件为速度入口和压力出口，并给出相应的湍动能和耗散率；模拟介质为空气，密度为10．6 kg／m3，使用当地大气压作为参考压力（本次研究关注的是压差变化，故参考压力的选择不会影响研究的目的）。由于清管器在管道内运动，本次研究以清管器为参考的对象，将其看成不动，所以在设置入口气速时需要减去清管器的速度，而管壁以清管器速度向反方向运动，即

1）入口速度为气相速度相对于清管器的速度Vg－Vpig；

2）管壁面运动速度为－Vpig；

3）压力出口以当地大气压为参考值，设为0。

此外，描述流动的无量纲数包括射流清管器旁通率φ、射流气体雷诺数Red2和管道中气体雷诺数ReD。

射流清管器的旁通率定义为

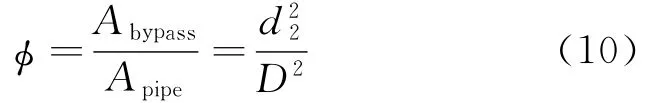
射流气体雷诺数定义为

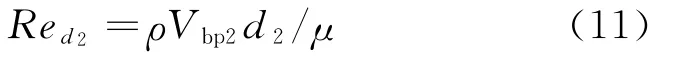
管道中气体的雷诺数定义为

式（10）～（12）中：Abypass为清管器射流通道的最小横截面积；Apipe为管道横截面积；μ为气体的动力黏度。

2．3 网格独立性验证

为了进行射流清管器网格独立性考核，对网格尺寸进行敏感性分析。以清管器旁通率5%为例，分别设置了3种网格尺寸：①网格1数量为998 300；②网格2数量为1 503 900；③网格3数量为2 527 942。图4为3种网格的中心轴线速度和总压分布曲线，图中的2条虚线分别表示清管器的入口和出口所对应的位置。从以上3种网格的敏感性分析可知，3种网格尺寸的模拟结果具有很好的一致性，选取网格2进行模拟分析。

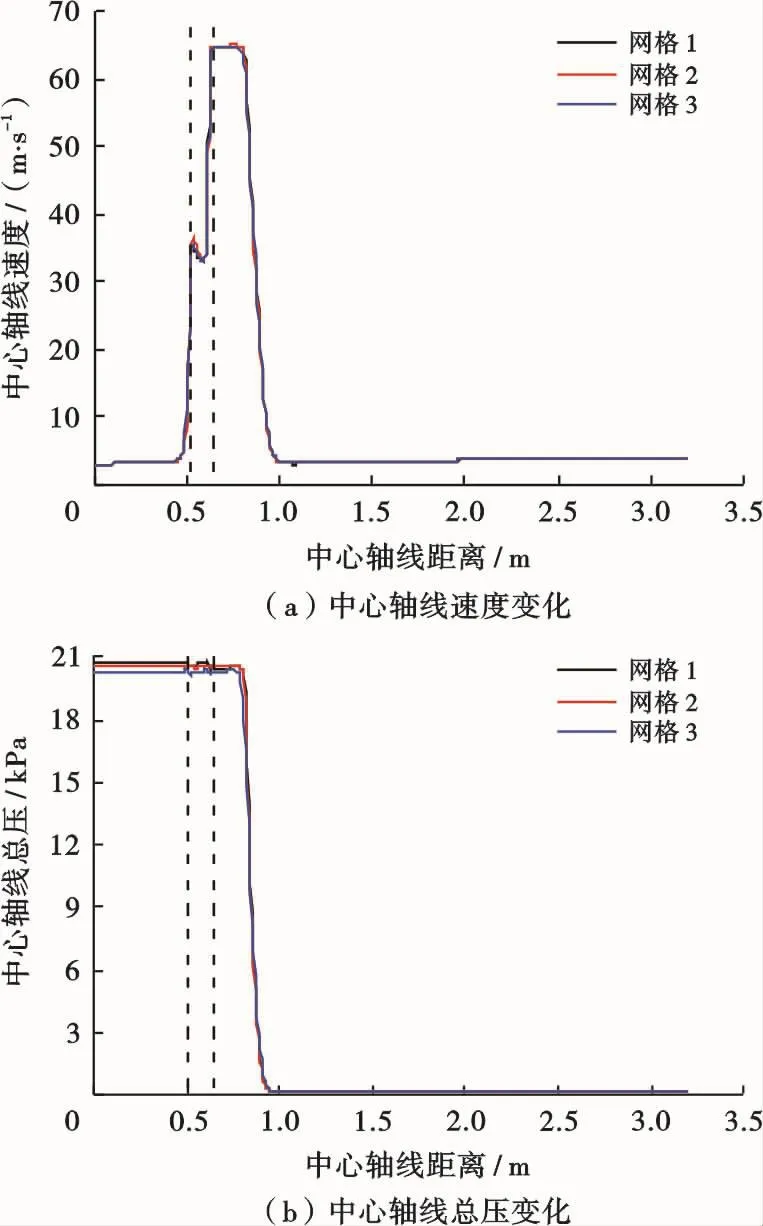
图4 射流清管器网格中心轴线速度和总压分布曲线Fig．4 Variation of the velocity and pressure along the axis of bypass pig

2．4 结果分析

为了寻求等效压降系数与运行参数之间的关联性，在同一旁通率、不同入口气速下研究等效压降系数与气体雷诺数的关系；为了探讨等效压降系数与清管器结构参数之间的关联性，在相同的入口气速下研究等效压降系数与旁通率变化的关系。

表1为本文方法计算和CFD模拟时射流清管器结构参数及运行工况条件。利用式（7）对表1的工况进行理论计算，且通过CFD模拟得出清管器前后的压差和最小射流通道中气体的动压，利用式（5）计算射流清管过程等效压降系数Keq2的变化规律，对比二者的差异。

表1 本文方法计算和CFD模拟时射流清管器结构参数和运行工况条件Table 1 Structure parameters and operation conditions of bypass pigging of this paper calculation method and CFD simulation

2．4．1 等效压降系数随射流气体雷诺数的变化规律

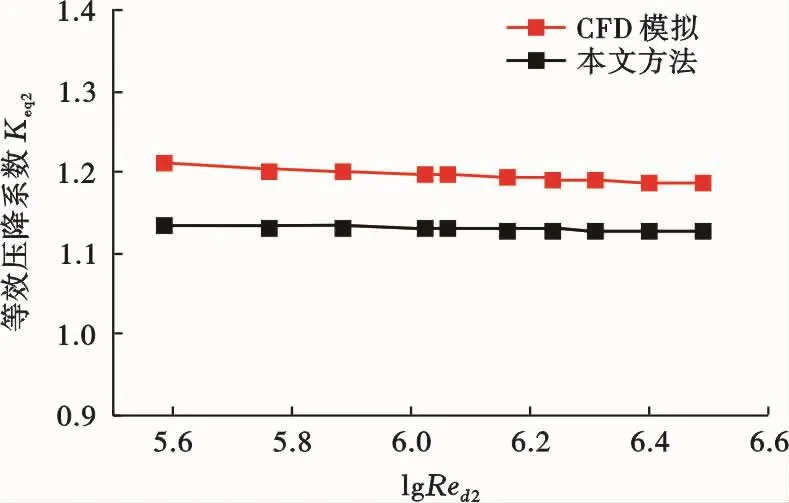
图5 射流清管器等效压降系数随气体雷诺数的变化（旁通率为10%条件下）Fig．5 Trend of equivalent pressure drop coefficient changed with the gas Reynolds number of bypass pig（bypass fraction of 10%）

图5 为射流清管器旁通率为10%时等效压降系数Keq2随射流气体雷诺数的变化规律。CFD模拟结果和本文方法计算结果均表明：在同一旁通率下，等效压降系数几乎不随雷诺数的增加而变化，这是由于射流清管器结构不变，等效压降系数的差异主要表现在不同雷诺数下气体通过射流管段的摩阻损失不同。随着雷诺数的增加，根据Churchill公式［17］可知：射流管两段摩擦系数f1、f2均减小，所以出现了等效压降系数随雷诺数增加而降低的现象，但由于摩阻损失在总的压降损失中的比重很低（占比1．7%～2．4%），其变化对于总压降的影响较小。这说明射流清管器的等效压降系数与运行工况之间的关系不大。通过偏差分析得：CFD模拟结果与理论模型计算结果的最大偏差在6．4%以内，表明本文建立的理论模型可以较好地计算射流清管器的等效压降系数。

利用本文模型计算得到：在等效压降系数的组成中，由突缩段的压降系数K1和突扩段的损失系数K2组成的结构突变总损失系数 K1（d2／d1）4＋K2占等效压降系数Keq2的94%，是对Keq2的主要贡献，因此对于特定的射流清管结构，其压降主要来自于流体通过突缩和突扩结构的能量损失；在突变结构中，突扩压降系数占比（70%）远大于突缩结构（24%），即流体通过射流清管器的能量损失主要源于突扩结构，这是由于流体通过突扩结构产生大回流区，导致流体介质动量产生强烈的交换，从而导致能量大幅度损失的结果。

2．4．2 等效压降系数随射流清管器旁通率的变化规律

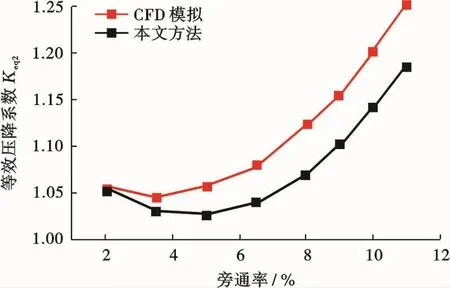
图6 射流清管器等效压降系数随旁通率的变化Fig．6 Trend of equivalent pressure drop coefficient changing with the bypass fraction of bypass pig

图6 为射流清管器在相同的入口气速下等效压降系数Keq2随旁通率的变化规律。本文方法计算结果与CFD模拟结果具有相同的变化趋势，即等效压降系数随着旁通率的增加出现微弱的减少阶段后呈快速上升趋势，并且二者的最大偏差在6%以内。分析式（7）可知，随着旁通率的增加（即A2增加），突缩结构的压降占比K1（A2／A1）2和磨擦项占比增大，渐缩结构压降占比φ（A2／A1－1）2和突扩结构压降占比K2减小。计算结果表明，当旁通率由2%增加至5%时，渐缩结构的压降减小程度（由6．7%减至3．4%）在总压降损失的比重最大，因而等效压降系数出现了减小的趋势；当继续增加旁通率时，突缩结构的压降占比K1（A2／A1）2快速增加，超过了突扩结构以及渐缩结构的压降减小程度，从而使等效压降曲线快速的增加。而且在总压降占比中，突缩结构的压降占比K1（A2／A1）2和突扩结构压降占比K2占主要部分，旁通率从2%增加至11%的过程中两突变结构的压降占比之和从91．71%增长至96．31%，这也表明在射流清管的等效压降系数的组成中突缩和突扩结构占据主要部分。

下面通过对式（7）作进一步的分析，研究等效压降系数Keq2与旁通率φ的定量关系。由于φ＝A2／Apipe，令ε＝Apipe／A1、a＝4f1L1／d1、b＝4f2L2／代入式（7）进行相应的变形与化简后可得

式（13）即为等效压降系数Keq2与旁通率φ的定量关系式。对于一个已知结构的射流清管器，其ε、φ、a、b均为与结构相关的常数。令C1＝K1ε2＋φε2＋aε2＋1、C2＝2εφ＋2、C3＝b、C4＝φ＋1，则式（13）可简化为

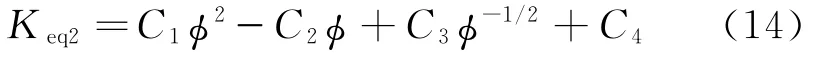
其中，C1、C2、C3、C4均为大于零的常数。对于本文研究结构，C1＝38．93、C2＝3．61、C3＝0．003 8、C4＝1．1，将这些数值代入式（14）并作图可得到等效压降系数与旁通率的定量关系曲线（图7）。从图7可知，对于一个特定结构的射流清管器，其等效压降系数与旁通率之间存在定量的关系，即随着旁通率的增加，等效压降系数呈现先减小而后快速增加的趋势。

图7 射流清管器等效压降系数与旁通率的定量关系曲线Fig．7 Quantitative relationship curve between equivalent pressure drop coefficient and bypass fraction of bypass pig

本文方法计算结果与CFD模拟结果的差异在于：首先使用式（7）进行等效压降系数计算时，摩擦损失计算式是在充分发展的湍流状态下推导得出的，而由于射流通道内部长度较短，在经历突缩过程后，流动还未达到充分发展的状态，而本文方法没有考虑这种流体运动状态；其次等效压降模型的建立是针对清管器不动的情况，而CFD模拟考虑了射流清管器在管道内的运动工况，考虑了运动的壁面效应对流线的影响。但从偏差数据可以看出，无论是对于雷诺数或旁通率变化的工况，二者的最大偏差均在6．4%以下；可见应用本文建立的等效压降系数模型可以较好地计算射流清管器的等效压降系数。因此，当选定一定结构的射流清管器后，通过测量相关的结构参数，可利用式（7）计算压降系数的数值，以此作为射流清管动态模拟的重要输入参数。

3 结论与建议

1）通过对射流清管过程进行动量和能量平衡分析，建立了射流清管等效压降系数计算模型，并利用CFD软件模拟计算了相同运行工况下的等效压降系数，通过对比等效压降系数随射流气体雷诺数与旁通率变化的关系，两者的吻合性较好，误差在6．4%以内。

2）研究结果表明，射流清管器等效压降系数随射流气体雷诺数的增加而微弱减少，基本不随雷诺数的变化而变化，随旁通率的增加出现先减小后快速增大的趋势，这说明等效压降系数主要取决于射流清管器的内部结构，是结构参数的函数。在射流通道的能量损失中，流体的能量损失包括突缩损失，突扩损失、渐缩能量损失、摩阻损失，由于突扩结构使流体形成大回流区域，占据了能量损失的主要部分，对能量损失的贡献最大，占总损失的比重约70%。

3）本文模型的建立过程忽略了气体管道中少量凝析液的存在，虽然射流清管过程中凝析液堆积于清管器前方的量大为减小，但相较于纯气相状态却增加了气液间的相互作用和气体通过的阻力，因而会增大清管器的驱动压差，使压降系数变大，因此在将来的研究中建议考虑少量凝析液的堆积对射流压降的影响。

［1］ OLANIYAN Y，LARREY D．Bypass pig modeling：A three phase gas condensate pipeline field case［C］．9th North Amer－ican Conference on Multiphase Technology．BHR Group，2014：499－512．

［2］ WU H L，SPRONSEN V G．Slug reduction with high by－pass pigs：a mature technology［C］．12th International Conference on Multiphase Production Technology．BHR Group，2005：313－325．

［3］ GROOTE G A，CAMP P B，VEENSTRA P，et al．By－pass pigging without or with speed control for gas－condensate pipelines［C］．Abu Dhabi International Petroleum Exhibition and Conference．2015．

［4］ ZHU X，ZHANG S，TAN G，et al．Experimental study on dynamics of rotatable bypass－valve in speed control pig in gas pipeline［J］．Measurement，2014，47（1）：686－692．

［5］ TAN T T，HUI R Y，YONG W R，et al．Speed control of pig using bypass flow in natural gas pipeline［C］∥Industrial Electronics，2001．Proceedings．ISIE2001．IEEE International Symposium on IEEE，2001：863－868．

［6］ TAN T T，SANG B K，HUI R K，et al．Modeling and simulation for pig with bypass flow control in natural gas pipeline［J］．KSME International Journal，2001，15（9）：1302－1310．

［7］ MONEY N，COCKFIELD D，MAYO S，et al．Dynamic speed control in high velocity pipelines［J］．PPSA Pipelines ＆ Gas Journal，2012，239（8）：30－38．

［8］ VAN SPRONSEN G，ENTABAN A，MOHAMAD A K，et al．Field experience with by－pass pigging to mitigate liquid surge［C］．16th International Conference on Multiphase Production Technology．BHR Group，2013：299－308．

［9］ LEE H S，AGUSTIAWAN D，JATI K，et al．Bypass pigging operation experience and flow assurance study［C］．Offshore Technology Conference．Houston，2012．

［10］ DONOGHUE O．Pigging as a flow assurance solution avoiding slug catcher overflow［C］．PPSA Seminar，2012．

［11］ ENTABAN A，ISMAIL A，JAMBARI M，et al．By－pass pigging：a‘simple’technology with significant business impact［C］．International Petroleum Technology Conference，2013．

［12］ BEUKER T，BROCKHAUS S，AHLBRINK R，et al．Addressing challenging environments－advanced in－line inspection solutions for gas pipelines［C］．24th World Gas Conference，Argentina，2009．

［13］ O＇DONOGHUE A．Pigging as a flow assurance solution：estimating pigging frequency for dewaxing［J］．Pipeline World，2004，49（2）：13－17．

［14］ AZPIROZ J E，HENDRIX M H W，BREUGEM W P，et al．CFD modelling of bypass pigs with a deflector disk［C］．17th International Conference on Multiphase Production Technology．BHR Group，2015：141－155．

［15］ SINGH A，HENKES R．CFD modeling of the flow around a by－pass pig［C］．8th North American Conference on Multiphase Technology．BHR Group，2012：229－243．

［16］ KUNDU P K，COHEN I M．Fluid mechanics，fourth edition［M］．Academic press，2008．

［17］ CHURCHILL S W．Friction－factor equation spans all fluidflow regimes［J］．Chemical engineering，1977，84（24）：91－92．

［18］ IDELCHIK I E．Handbook of hydraulic resistance，3rd edition［M］．CRC Press Inc，Begell House Inc，1994．

［19］ TEYSSANDIER R G，WILSON M P．An analysis of flow through sudden enlargements in pipes［J］．Journal of Fluid Mechanics，1974，64（1）：85－95．

Development and verification of a model to compute the equivalent pressure drop coefficient of bypass pigs

CHEN Jianheng1HE Limin1LUO Xiaoming1LI Qingping2
（1．Provincial Key Laboratory of Oil ＆ Gas Storage and Transportation Safety，China University of Petroleum，Qingdao，Shandong266580，China；2．CNOOC Research Institute，Beijing100028，China）

A computation model for equivalent pressure drop coefficient was developed by analysis on momentum and energy balance during bypass pigging process．The CFD simulation for the same process was conducted to analyze and verify the relationships between the equivalent pressure drop coefficient and bypass fraction as well as between the coefficient and Reynolds number of bypass gas．The study shows the coefficient has a tendency of slight decrease then rapid increase with the rise of bypass fraction；and at the same bypass fraction，the coefficient hardly changes with the Reynolds number of bypass gas．The sudden expansion structure accounts for the largest portion of the whole pressure drop across the bypass pig，close to70%．Deviations between the result of computation model developed in this paper and that of CFD simulation are within 6．4%，which indicates the model can be reasonably used to compute the equivalent pressure drop coefficient of bypass pigs，which is an important parameter input for bypass pig dynamic simulation．The research result is of great significance for the design optimization and prototype modification of bypass pigs．

bypass pig；equivalent pressure drop coefficient；computation model；CFD simulation verification；bypass fraction；Reynolds number

TE832

A

陈建恒，何利民，罗小明，等．射流清管器等效压降系数模型的建立及分析验证［J］．中国海上油气，2017，29（5）：134－140．

CHEN Jianheng，HE Limin，LUO Xiaoming，et al．Development and verification of a model to compute the equivalent pressure drop coefficient of bypass pigs［J］．China Offshore Oil and Gas，2017，29（5）：134－140．

1673－1506（2017）05－0134－07

10．11935／j．issn．1673－1506．2017．05．019

＊“十三五”国家科技重大专项“深水天然气凝析液控砂与射流清管技术（编号：2016ZX05028－004－003）”部分研究成果。

陈建恒，男，硕士研究生，现主要从事多相管流及油气田集输技术的研究工作。地址：山东省青岛市黄岛区长江西路66号（邮编：266580）。E－mail：s15060742＠s．upc．edu．cn。

何利民，男，教授，博士生导师，主要从事多相管流及油气田集输技术的研究工作。地址：山东省青岛市黄岛区长江西路66号（邮编：266580）。E－mail：helimin＠upc．edu．cn。

2017－01－03 改回日期：2017－04－17

（编辑：叶秋敏）