拉格朗日中值定理的应用实例
2017-11-04陈少云
陈少云
(四川建筑职业技术学院 信息工程系,四川 德阳 618000)
拉格朗日中值定理的应用实例
陈少云
(四川建筑职业技术学院 信息工程系,四川 德阳 618000)
简要介绍了拉格朗日中值定理的内容、几何意义和推论,通过大量例子阐明如何应用拉格朗日中值定理证明等式和不等式.
拉格朗日中值定理;推论;等式;不等式
0 引言
拉格朗日中值定理是微分学中的基本定理之一,反映了可导函数在闭区间上整体的平均变化率与区间内某点的局部变化率之间的关系,导数应用中的许多判定定理由它证明.拉格朗日中值定理是罗尔中值定理的推广,同时也是柯西中值定理的特殊情形.因此,它是微积分教学中的重要内容,但其应用也是学习者的难点,下面通过展示大量例子,希望能较全面地概括其应用,给教学双方以启发.
1 拉格朗日中值定理及其几何意义
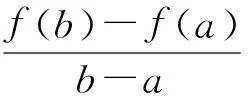
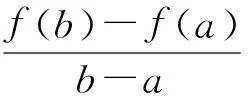
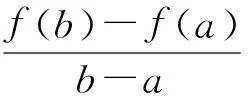
其结论也可写成:在(a,b)内至少存在一点ξ,使得f(b)-f(a)=(b-a)f′(ξ).
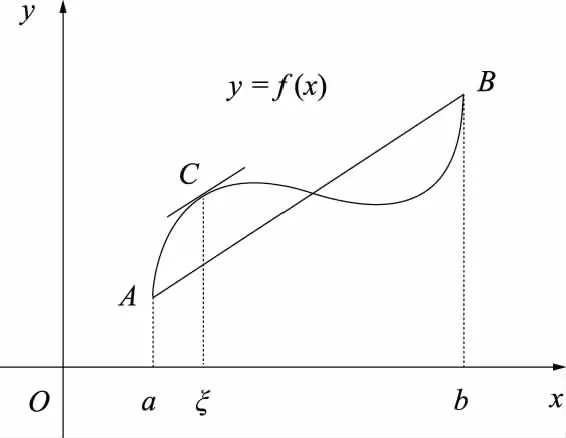
图1 拉氏定理的几何意义Fig1 Geometric meaning of Lagrange Theorem
几何意义[1-5]如图1,若连续曲线y=f(x)在点A(a,f(a))和B(b,f(b))之间的每一点处都有不垂直于x轴的切线,则在A、B之间的曲线上至少存在一点C(ξ,f(ξ)),使得该点处的切线与割线AB平行.
显然,罗尔定理(如果函数y=f(x)在[a,b]上连续,在(a,b)内可导,且f(a)=f(b),则在(a,b)内至少存在一点ξ,使得f′(ξ)=0)是拉格朗日中值定理的特殊情形.
推论1[3]若函数y=f(x)不是常数函数,y=f(x)在[a,b]上连续,在(a,b)内可导,且f(a)=f(b),则在(a,b)内至少存在一点ξ,使得f′(ξ)<0(或f′(ξ)>0).
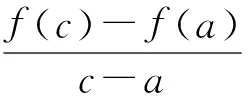
又f(a)=f(b),f(x)不为常数函数,则f(c)-f(a)和f(b)-f(c)异号,从而f′(ξ)f′(η)<0,因此命题得证.
推论2[1-5]如果函数f(x)在区间I上的导数恒为零,那么f(x)在区间I上为常数函数.
证明设∀x1,x2∈I,不妨设x1 根据已知,f(x)在[x1,x2]上满足拉格朗日定理条件,从而存在ξ∈(x1,x2),使得 又f′(ξ)=0,所以f(x2)=f(x1). 即在区间I上任意两点的函数值都相等,因此f(x)在区间I上为常数函数. 证明令F(x)=xf(x),则F′(x)=f(x)+xf′(x). 由已知F(x)在[a,b]上满足拉格朗日定理条件,所以在(a,b)内至少存在一点ξ,使得F(b)-F(a)=F′(ξ)(b-a),即 若f(x)在区间[a,b]上满足拉格朗日定理条件,则f(b)-f(a)=f′(ξ)(b-a),a<ξ 又0 证明令f(t)=tant,则f′(t)=sec2t. 又0<ξ 例7[1]证明: arctana-arctanb≤a-b. 例8[3]证明:arcsinx1-arcsinx2≥x1-x2. 显然,f(x)在[x1,x2]或[x2,x1]上满足拉格朗日定理条件,所以介于x1与x2之间必有一点ξ,使得 即 因此 arcsinx1-arcsinx2≥x1-x2. 例9[2]证明:sinx-siny≤x-y. 证明令f(t)=sint,则f′(t)=cost. 显然,f(t)在[x,y]或[y,x]上满足拉格朗日定理条件,所以介于x与y之间必有一点ξ,使得sinx-siny=cosξ(x-y),即sinx-siny=cosξ·x-y. 又cosξ≤1,所以 cosξ·x-y≤x-y, 而 cosξ·x-y=sinx-siny, 因此 sinx-siny≤x-y. [1] 同济大学数学系. 高等数学:上册[M].6版.北京:高等教育出版社,2007:129-134. [2] 赵树嫄.经济应用数学基础(一)微积分[M].3版.北京:中国人民大学出版社,2012:120-124. [3] FINNEY,WEIR,GIORDANO.托马斯微积分[M].北京:高等教育出版社,2003:237-244. [4] 李天然.高等数学(建工类)[M].北京:高等教育出版社,2008:107-110. [5] 陈少云.经济数学[M].北京:高等教育出版社,2016:67-70. [6] 同济大学数学系. 高等数学附册学习辅导与习题选解(上下册合订本)[M]. 6版.北京:高等教育出版社,2007:62-64. ApplicationExamplesofLagrange’sMeanValueTheorem CHEN Shaoyun (DepartmentofInformationEngineering,SichuanCollegeofArchitecturalTechnology,Deyang618000,China) The contents, its geometric meaning and deduction of Lagrange’s Mean Value Theorem are briefly introduced first in this article. Then with some examples the article illustrates how to prove the equalities and inequalities by Lagrange’s Mean Value Theorem. Lagrange’s Mean Value Theorem; deduction; equality; inequality 2017-07-09 陈少云(1969—),男,重庆合川人,四川建筑职业技术学院信息工程系副教授,主要研究方向:计算数学和高等数学教育. 10.3969/j.issn.1007-0834.2017.03.012 O172.1 A 1007-0834(2017)03-0054-04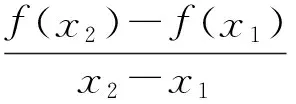
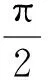
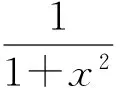
2 应用拉格朗日中值定理证明含导数的等式
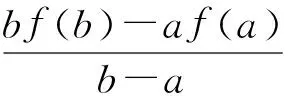
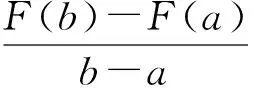
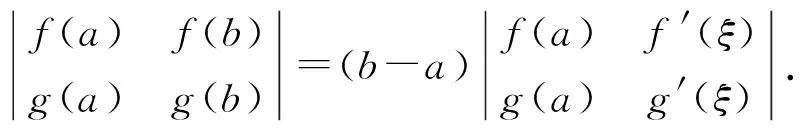
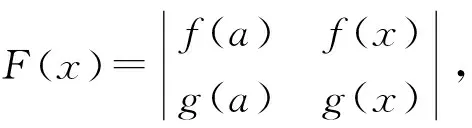
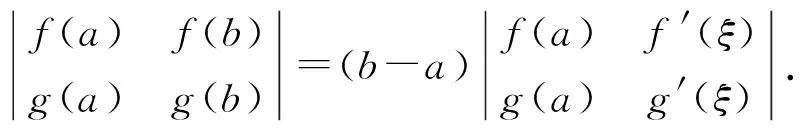
3 利用拉格朗日中值定理证明不等式