一种带分布参数的区间粗糙数多属性决策方法
2017-11-04黄锐露吕跃进
田 瑾,黄锐露,吕跃进
(广西大学 a.电气工程学院; b.数学与信息科学学院,南宁 530004)
一种带分布参数的区间粗糙数多属性决策方法
田 瑾a,黄锐露b,吕跃进b
(广西大学 a.电气工程学院; b.数学与信息科学学院,南宁 530004)
本文定义了带分布参数的区间粗糙数的运算法则和新的可能度公式,并证明了新的可能度公式满足的一些性质.其次,基于带分布参数的区间粗糙数间的序关系,将已提出的区间粗糙数加权集结算子推广至带分布参数的区间粗糙数有序加权集结算子.最后,基于新的可能度公式及有序加权集结算子,提出了一种解决属性权重未知时多属性决策问题的算法,并通过实例说明了算法的有效性和合理性.
带分布参数的区间粗糙数;可能度;有序加权集结算子;多属性决策
0 引言
多属性决策的实质是决策者根据一定的排序规则从有限个备选方案中选择出最优(满意)的行动方案.由于受客观事物的复杂性和不确定性、人类思维的模糊性以及心理状态等因素的影响,多属性决策的偏好信息会出现不同程度的模糊性和不确定性,通常以区间数、三角模糊数、梯形模糊数、语言、直觉模糊数等形式表达.
1982年,Pawlak[1]提出粗糙集理论,它是一种新的处理模糊和不确定性知识的数学工具.至今为止,其成果已被广泛地应用到决策分析、机器学习、数据挖掘与模式识别、过程控制等方面.区间粗糙数是用区间刻画下近似和上近似的粗糙集.在很多实际的多属性决策问题中,属性值可通过形如的区间粗糙数表示.例如某生产决策问题中产品的生产成本、库存成本以及期望收益;物流系统配送中心选址问题中的期望收益、管理效益、风险规避等.假设某项目的投资额用一个区间粗糙数来表示,其解释为该项目的投资额落在3万到8万之间是肯定的,但是有很大概率落在5万到7万之间.
曾智和曾华[2]给出了区间粗糙数加权期望的定义及相关性质,提出了基于区间粗糙数加权期望值的多属性决策方法.钱伟懿和曾智[3]补充了区间粗糙数的运算法则,定义了加权平均算子与加权几何算子及其性质,给出区间粗糙数两两比较的可能度公式及其相关性质,提出一种基于可能度的区间粗糙数排序方法.靳宗伟[4]定义了区间粗糙数的欧氏距离和期望值,以及区间粗糙数的L-测度,基于此测度给出了区间粗糙数的排序方法.曾雪兰和谢凤平[5]定义了正态分布的区间粗糙数,补充了联系数的运算法则,建立了区间粗糙数的均值-方差联系数模型,提出了一种基于连续数的区间粗糙数多属性决策方法.此外,谢凤平和曾雪兰等[6]给出了区间粗糙数互补和互反判断矩阵的相互转化公式,提出了一种基于可能度的区间粗糙数互补判断矩阵的排序方法.翁士洲和吕跃进[7]首次定义了带分布参数的区间粗糙数以及排序方法.夏晓东和吕跃进[8]定义了带参数的区间粗糙数的期望和方差,提出了一种积分形式的带参数的新的区间粗糙数相离度定义,给出一种基于熵值法及相离度的含参数型区间粗糙数多属性决策方法.
鉴于现有文献对区间粗糙数的研究还处于初步阶段,本文希望在借鉴他人研究成果的基础上进行一些新的研究,定义了带分布参数的区间粗糙数的相关运算法则及可能度公式,提出了带分布参数的区间粗糙数加权算术平均算子和加权几何算子,并将其推广得到带分布参数的区间粗糙数有序加权平均算子和有序加权几何算子.针对属性值为带分布参数的区间粗糙数且属性权重未知的情况,提出了一种新的多属性决策方法.
1 基本定义
1.1区间粗糙数的一些基本定义
定义1[9]设U为论域,X⊂U为表示某个概念的集合,则X的下近似和上近似分别定义为
其中:R(x)={y∈U|y~x},R-1(x)={y∈U|y~x},~为某二元相似关系(具有自反性,但不具有对称性和传递性).
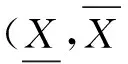
定义3[3]设ηi=([ai,bi],[ci,di])(i=1,2)为两个区间粗糙数,k>0,则有
1)η1+η2=([a1+a2,b1+b2],[c1+c2,d1+d2]);
2)kη1=([ka1,kb1],[kc1,kd1]);
3)η1·η2=([a1a1,b1b2],[c1c2,d1d2]);
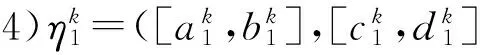
1.2一些基本集结算子的定义
设I为全体区间粗糙数组成的集合.
定义4[3]设ηi=([ai,bi],[ci,di])(i=1,2,…,n)为一组区间粗糙数,令IRWAA:In→I为
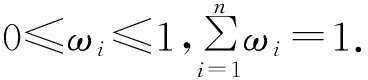
定义5[3]设ηi==([ai,bi],[ci,di])(i=1,2,…,n)为一组区间粗糙数,令IRWGA:In→I为
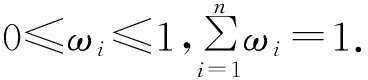
2 带分布参数的区间粗糙数及集结算子
2.1带分布参数的区间粗糙数的定义
定义6[7]η=([a,b],[c,d],α)为一个带分布参数的区间粗糙数,若η满足如下条件:
1)η′=([a,b],[c,d])为一个区间粗糙数;
2)P(x[a,b])=α,P(x[c,d][a,b])=P(x[c,a]∪[b,d])=1-α;
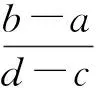
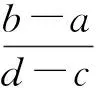
进一步地,若假设考察值在外区间与内区间之差[c,d][a,b])=[c,a]∪[b,d])上的分布为均匀分布,则有
P(x[c,a])=(1-α),P(x[b,d])=(1-α).
(1)
则带分布参数的区间粗糙数可以进一步表示为({[c,a],P[c,a]},{[a,b],P[a,b]},{[b,d],P[b,d]}),
其中P[c,a]=P(x[c,a]),P[a,b]=P(x[a,b]),P[b,d]=P(x[b,d]),且有P[c,a]+P[a,b]+P[b,d]=1,即满足分布参数之和等于1.
定义7 设ηi=({[ci,ai],P[ci,ai]),({ai,bi},P[ai,bi]),({bi,di},P[bi,di])(i=1,2,…,n)为一组带分布参数的区间粗糙数,k>0,定义如下运算:
2)kηi=({[kc1,ka1],P[c1,a1]},{[ka1,kb1],P[a1,b1]},{[kb1,kd1],P[b1,d1]});
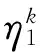
定理1 ①由定义7运算1)至运算4)得到的新的区间粗糙数仍满足分布参数之和等于1;②运算1)和运算3)满足交换律;③当n=2时,运算2)对运算1)满足分配律且运算4)对运算2)也满足分配律.
证明①,②,③可由定义7易证,故证明略.
2.2带分布参数的区间粗糙数的可能度公式
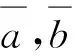
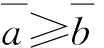
定义8中的可能度公式具有的性质如下:
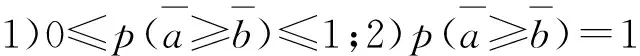
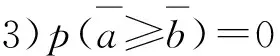
定义9 设ηi=({[ci,ai],P[ci,ai]},{[ai,bi],P[ai,bi]},{[bi,di],P[bi,di]})(i=1,2)为两个带分布参数的区间粗糙数,定义:
P(η1≥η2)=P[c1,a1]P[c2,a2]p([c1,a1]≥[c2,a2])+P[c1,a1]P[a2,b2]p([c1,a1]≥[a2,b2])+P[c1,a1]P[b2,d2]p([c1,a1]≥[b2,d2])+P[a1,b1]P[c2,a2]p([a1,b1]≥[c2,a2])+P[a1,b1]P[b2,b2]p([a1,b1]≥[a2,b2])+P[a1,b1]P[b2,d2]p([a1,b1]≥[b2,d2])+P[b1,d1]P[c2,a2]p([b1,d1]≥[c2,a2])+P[b1,d1]P[a2,b2]p([b1,d1]≥[a2,b2])+P[b1,d1]P[b2,d2]p([b1,d1]≥[b2,d2])
定理2 设ηi=({[ci,ai],P[ci,ai]},{[ai,bi],P[ai,bi]},{[bi,di],P[bi,di]})(i=1,2,3)为带分布参数的区间粗糙数,定义9中的可能度公式具有的性质如下:
1)0≤P(η1≥η2)≤1;
2)P(η1≥η2)+P(η2≥η1)=1;
3)P(η1≥η2)=1,当且仅当d2≤c1;
4)P(η1≥η2)=0,当且仅当d1≤c2;
5)若P(η1≥η2)=1,P(η2≥η3)=1,则P(η1≥η2)=1.
证明1)证明略.
P(η1≥η2)+P(η2≥η1)=≤P[c1,a1]P[c2,a2]+P[c1,a1]P[a2,b2]+P[c1,a1]P[b2,d2]+P[a1,b1]P[c2,a2]+P[a1,b1]P[a2,b2]+P[a1,b1]P[b2,d2]+P[b1,d1]P[c2,a2]+P[b1,d1]P[a2,b2]=P[c1,a1]P[a1,b1]+P[b1,d1]=1.
熟悉常用量具的性能和使用方法,掌握产品各项技术指标,严格执行企业标准、检验规程,进行产品加工过程的质量检验和控制,以及产品的实验和测试,对生产加工过程中出现的产品质量问题进行处理和分析,并及时反馈,针对现场做好制程解析,并进行改善活动,严格执行各项规章制度和工作纪律,树立服务生产的意识。
3) 先证明d2≤c1⟹P(η1≥η2)=1.由d2≤c1得到
p([c1,a1])≥[c2,a2]=1;p([c1,a1])≥[a2,b2]=1;p([c1,a1])≥[b2,d2]=1; 也即
p([a1,b1])≥[c2,a2]=1;p([a1,b1])≥[a2,b2]=1;p([a1,b1])≥[b2,d2]=1;
p([b1,d1])≥[c2,a2]=1;p([b1,d1])≥[a2,b2]=1;p([b1,d1])≥[b2,d2]=1.
故有
P(η1≥η2)=P[c1,a1]P[c2,a2]+P[c1,a1]P[a2,b2]+P[c1,a1]P[b2,d2]+P[a1,b1]P[c2,a2]+
P[a1,b1]P[a2,b2]+P[a1,b1]P[b2,d2]+P[b1,d1]P[c2,a2]+P[b1,d1]P[a2,b2]+P[a1,b1]P[b2,d2],
于是有
P(η1≥η2)=P[c1,a1](P[c2,a2]+P[a2,b2]+P[b2,d2])+P[a1,b1](P[c2,a2]+P[a2,b2]+P[b2,d2])+
P[b1,d1](P[c2,a2]+P[a2,b2]+P[b2,d2]),
因此有P(η1≥η2)=P[c1,a1]+P[a1,b1]+P[b1,d1]=1.
下面证明P(η1≥η2)=1⟹d2≤c1.
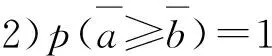
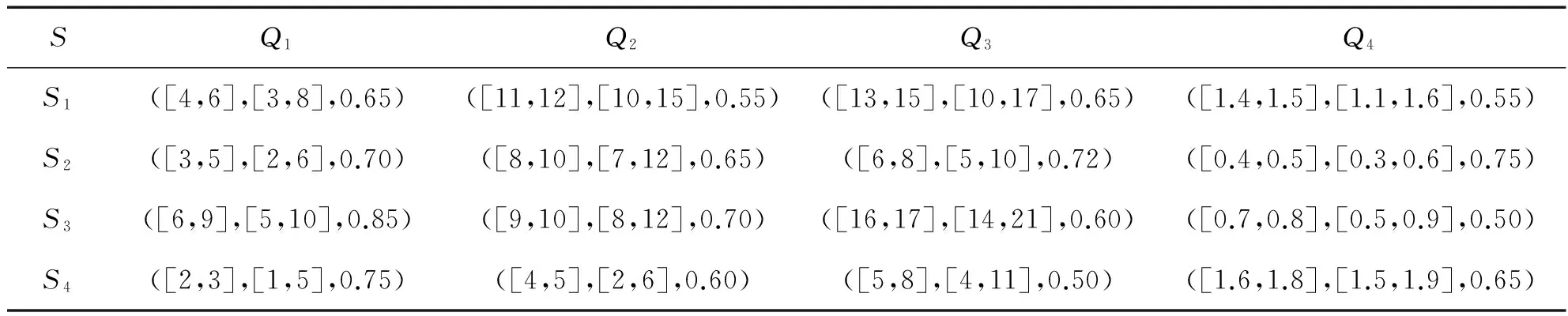
P(η1≥η2) P[a1,b1]P[a2,b2]+P[a1,b1]P[b2,d2]+P[b1,d1]P[c2,a2]+P[b1,d1]P[a2,b2]+P[a1,b1]P[b2,d2]=P[c1,a1]+P[a1,b1]+P[b1,d1]=1, 与已知P(η1≥η2)=1矛盾. 故假设不成立.即P(η1≥η2)=1⟹d2≤c2成立. 综上,P(η1≥η2)=1,当且仅当d2≤c1. 4)和5)可由2)和3)易证. 2.3带分布参数的区间粗糙数的集结算子 设IWDP为全体带分布参数的区间粗糙数组成的集合. 基于带分布参数的区间粗糙数的可能度定义9,可得到该组带分布参数的区间粗糙数的两两比较可能度矩阵.由定理2中的性质2)可知,其为互补判断矩阵.由互补判断矩阵可得到带分布参数的区间粗糙数之间的序关系.基于此序关系,将定义10、定义11推广至有序加权集结算子,可得如下定义: 其中ω=(ω1,ω2,…,ωn)是与函数WDPIROWAA相关联的加权向量,ωj且ζj是该组区间粗糙数(η1,η2,…,ηn)中第j大的元素,则称函数WDPIROWAA是n维带分布参数的区间粗糙数有序加权算术平均算子,也称为WDPIROWAA算子. 其中ω=(ω1,ω2,…,ωn)是与函数WDPIROWAA相关联的加权向量,ωj且ζj是该组区间粗糙数(η1,η2,…,ηn)中第j大的元素,则称函数WDPIROWGA是n维带分布参数的区间粗糙数有序加权算术平均算子,也称为WDPIROWGA算子. 常见的决策矩阵的属性值有效益型和成本型两种,为了统一各属性值对决策目标的效用值评价,将决策矩阵进行规范化处理,对属性值为带分布参数的区间粗糙数的决策矩阵,给出下面的规范化处理方法: 对于效益型属性而言,其转化公式如下: 对于成本型属性而言,其转化公式如下: 其中:i=1,2,…,m;j=1,2,…,n. 检验带分布参数的区间粗糙数是否满足定义6,并根据公式(1)将带分布参数的区间粗糙数转换为如下形式: rij=({[cij,aij],P[cij,aij]},{[aij,bij],P[aij,bij]},{[bij,dij],P[bij,dij]})(i=1,2,…,m;j=1,2,…,n), 设此时得到的区间粗糙数决策矩阵为R=(rij)m×n. 为了求解序权重,构建下面的最小偏差平方(LDS)模型[12]: 综上所述,可设计如下区间粗糙数多属性决策算法: Step1 将决策矩阵A=(ζij)m×n转化为规范化的决策矩阵R=(rij)m×n. Step2 由LDS模型得到序权重ω. Step3 对i从1到m遍历,记规范化的决策矩阵R的第i行为Ri,利用定义9所给出的可能度公式得到Ri中两两比较的可能度矩阵Pi=(pkl)n×n,利用互补判断矩阵的排序公式[13] 得到Ri的排序结果. Step4 分别利用WDPIROWAA、WDPIROWGA集结算子对方案进行集结,得到集结结果zi(ω),i=1,2,…,m. Step5 对集结结果zi(ω),i=1,2,…,m.利用定义9所给出的可能度公式得到两两比较的可能度矩阵,利用上述互补判断矩阵的排序公式进行排序,进而得到最终的排序结果. 考虑某个公司对产品投资项目的选择问题,设有4个备选投资项目(方案)Si(i=1,2,3,4)可供选择,对备选投资项目主要以期望收益Q1,风险盈利Q2,投资成本Q3,风险损失Q4等4个评估指标(属性)进行评价,从中选出最佳方案.这些指标前三个为效益型属性,后一个为成本型属性,本例对应的评价数据如表1所示. 表1 决策矩阵 Step1 根据效益型属性和成本型属性的转化公式,得到规范化后的决策矩阵(只列出部分),如表2所示. 表2 规范化后的决策矩阵 Step2 由LDS模型得到的属性序权重:ω=(0.7807,0.1573,0.04335,0.0186) . Step3 每一行由两两比较的可能度矩阵得到的排序结果: Step4 由WDPIROWAA算子集结后的结果: 同理,可得到由WDPIROWGA算子集结后的结果. Step5 由WDPIROWAA算子集结后的结果两两比较得到的可能度矩阵: 同理,可得到由WDPIROWGA算子集结后的结果,及其两两比较得到的可能度矩阵. Step6 得到WDPIROWAA集结算子最终的排序结果均为S2>S3>S1>S4. 同理,可得到由WDPIROWGA集结算子的最终排序结果与上一致. 本文研究了带分布参数的区间粗糙数的多属性决策问题,补充了带分布参数的区间粗糙数的运算法则,定义了较为合理的可能度公式,提出了带分布参数的区间粗糙数的一些集结算子.在权重未知的情况下,通过最小偏差平方模型进行权重求解,利用有序加权集结算子进行信息集结,再根据可能度矩阵和排序公式对方案进行排序,选择出最佳方案,并通过实例验证了算法的有效性和合理性.此外,李敬等[14]研究了基于优势度的序信息系统属性重要性度量.本文接下来的研究可将序信息系统拓展为基于带分布参数的区间粗糙数序信息系统,研究其属性重要性度量及属性约简与规则提取. [1]PAWLAK Z.Rough sets[J].International Journal of Computer & Information Sciences,1995,38(11):88-95. [2]曾智,曾华.基于区间粗糙数加权期望多属性决策方法[J].科技信息,2012(11):252-253. [3]钱伟懿,曾智.基于可能度的区间粗糙数排序方法[J].运筹与管理,2013,22(1):71-76. [4]靳宗伟.基于区间粗糙数的多属性决策方法研究[D].南宁:广西大学, 2013. [5]曾雪兰,谢凤平.基于联系数的区间粗糙数多属性决策方法[J].计算机工程与应用,2017,53(3):54-57. [6]谢凤平,曾雪兰,段云艳.基于区间粗糙数互补判断矩阵的一种排序方法[J].琼州学院学报,2015,22(5):22-26. [7]翁世洲,吕跃进.区间粗糙数的排序方法及其应用[J].南京大学学报(自然科学版),2015(4):818-825. [8]夏晓东,吕跃进.一种带参数的区间粗糙数型多属性决策方法[J].计算机工程与应用,2017,3(5):255-259. [9]SLOWINSKI R,VANDERPOOTEN D.A generalized definition of rough approximations based on similarity[J].IEEE Transactions on Knowledge & Data Engineering,2000,12(2):331 - 336. [10]LIU B.Theory and Practice of Uncertain Programming[J].Studies in Fuzziness & Soft Computing,2002, 102(4):295-318. [11]徐泽水,达庆利.区间数排序的可能度法及其应用[J].系统工程学报,2003,18(1):67-70. [12]王小楠,徐迎军,尹世久.有序加权平均算子权重确定新方法及其应用[J].聊城大学学报(自然科学版),2014, 27(2):82-87. [13]徐泽水.模糊互补判断矩阵排序的一种算法[J].系统工程学报,2001,16(4):311-314. [14]李敬,王利东,李晓庆,等.基于优势度的序信息系统属性重要性度量[J].琼州学院学报,2015,22(5):17-21. AMultipleAttributeDecisionMakingMethodofIntervalRoughNumberswithDistributionParameters TIAN Jina, HUANG Rui - lub, LV Yue - jinb (a.College of Electrical Engineering;b.College of Mathematics and Information Science,Guangxi University, Nanning 530004, China) This paper, first of all,defines the operational rules and the new possibility degree formula of the interval rough numbers with distributed parameters, and then proves some properties of the new possibility degree formula.Secondly, based on the rank correlation of interval rough numbers with distribution parameters, the existing weighted aggregate operator about interval rough number is extended to ordinal weighted aggregation operator of interval rough number with distributed parameters.Finally, based on the new possibility degree formula and the ordinal weighted aggregate operator, an algorithm is proposed to solve the multiple attribute decision making problems with unknown attribute weight, and the effectiveness and feasibility of the algorithm is illustrated by an example. interval rough numbers with distribution parameters; possibility degree; ordinal weighted aggregation operator; multiple attribute decision making 格式:田瑾,黄锐露,吕跃进.一种带分布参数的区间粗糙数多属性决策方法[J].海南热带海洋学院学报,2017,24(5):56-62. 2017-09-25 国家自然科学基金资助项目(71361002) 田瑾(1990-),女,陕西西安人,广西大学电气工程学院管理科学与工程专业2015级硕士研究生,研究方向为管理决策. 吕跃进(1958-),男,广东龙川人,广西大学数学与信息科学学院教授,硕士,研究方向为粗糙集、数据挖掘、管理决策. N94,C934 A 2096-3122(2017) 05-0056-07 10.13307/j.issn.2096-3122.2017.05.10 (编校曾福庚)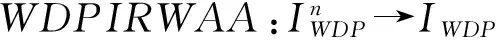
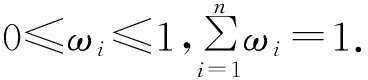
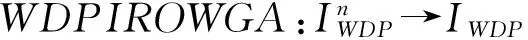
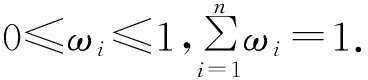
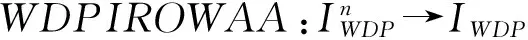
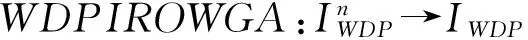
3 基于WDPIROWAA、WDPIROWGA集结算子的区间粗糙数多属性决策方法
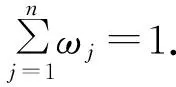
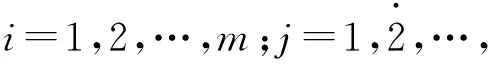
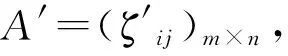
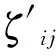
4 应用案例

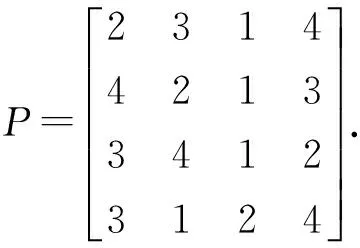
5 结语
