同步发电机非线性励磁系统模糊滑模控制研究
2017-11-03闵国君
陈 金,张 孝,王 平,闵国君,梁 铃,陈 峰
(1.贵州电网有限责任公司电力调度控制中心,贵州 贵阳 550002;2.南京南瑞继保工程技术有限公司电网应用部,江苏 南京 211102)
同步发电机非线性励磁系统模糊滑模控制研究
陈 金1,张 孝2,王 平1,闵国君2,梁 铃1,陈 峰2
(1.贵州电网有限责任公司电力调度控制中心,贵州 贵阳550002;2.南京南瑞继保工程技术有限公司电网应用部,江苏 南京211102)
同步发电机励磁系统是一个具有时变性、多时滞环节以及高度非线性的复杂控制系统,其运行是否可靠直接影响到整个电力系统运行的稳定性。因此,对发电机励磁系统进行有效的控制至关重要。针对发电机励磁系统运行时的动静态性能要求,提出一种模糊滑模复合控制策略。滑模控制以其对干扰和摄动的不变性等优点,可以有效地解决发电机励磁控制的鲁棒性问题,并可保证系统的全局渐进稳定性;同时,采用指数趋近律的方法,可以使系统在趋近运动段快速到达切换面。模糊控制能够模仿人的经验对复杂对象进行专家控制。将其应用于励磁控制中,可以提供更佳的阻尼效果,减少滑模运动产生的抖振,提高扰动下的动态品质。为验证算法效果,利用MATLAB进行仿真。仿真结果表明,与单纯的滑模控制相比,该控制算法可加快发电机励磁系统的响应速度,增强鲁棒性,有效地提高了电力系统的稳定性。
同步发电机; 非线性; 励磁系统; 模糊控制; 滑模控制; 复合控制; 自适应; MATLAB
0 引言
为应对发电机励磁系统的非线性与时变性,具有较强自适应、自学习能力的智能控制技术,在发电机励磁系统控制中已得到越来越多的应用[1-6]。文献[7]采用规则自适应模糊控制,改善了励磁系统的稳定性,但其稳态精度低,不适用于复杂系统。文献[8]将神经网络应用于励磁控制,自适应能力强,但计算量大,且不能保证收敛。文献[9]将专家控制用于励磁系统,控制处理灵活,但自学习能力差。文献[10]采用迭代学习控制,可以处理励磁系统非线性、时变性问题,但当存在噪声或非重复性干扰时,系统稳定性会降低。
因此,针对上述控制方法存在的问题,本文提出了一种结合模糊和滑模的复合控制方法,将其应用于励磁系统。MATLAB仿真结果验证了所提方法的有效性和可行性。
1 励磁控制系统模型
同步发电机励磁控制系统通常由励磁调节器、功率放大单元、同步发电机和电压测量单元等部件组成。
发电机励磁系统模型如图1所示。

图1 发电机励磁系统模型框图
图1中:U0为发电机参考电压;Uf为励磁电压;UF为发电机输入励磁电压;U为发电机机端电压。
本文对同步发电机励磁控制系统进行适当的简化。以励磁系统动态特性为基础,各单元简化模型如下。
1.1同步发电机模型
忽略发电机磁路饱和现象,同步发电机的数学模型可以简化为一阶滞后环节,其传递函数为:

(1)
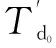
1.2功率放大单元模型
励磁调节器输出的控制信号Uf经过功率放大单元,输出满足发电机输入要求的信号UF。其数学模型可以简化为一阶惯性环节,其传递函数为:

(2)
式中:Kp为电压放大系数;Tp为电压放大时间常数。
1.3电压测量单元模型
同步发电机输出电压U经过电压测量单元得到励磁调节器输入信号,其数学模型可以简化为一阶惯性环节。其传递函数为:
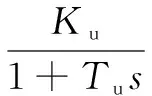
(3)
式中:Ku为比例系数;Tu为滤波回路时间常数。
2 模糊滑模励磁控制器的设计
控制器以同步发电机机端电压的误差作为控制器的输入。滑模控制(slidingmodecontrol,SMC)器以发电机机端电压的误差及其积分项作为状态变量,具有较强的鲁棒性;同时,在趋近运动段采用指数趋近律,可快速跟踪给定信号。模糊控制器(fuzzycontroller,FC)对发电机机端电压的误差及其变化率进行模糊化处理,并经过反模糊化得到模糊控制器的输出。滑模变结构控制器的输出和模糊控制器的输出共同组成了模糊滑模控制器的输出控制量,再经过功率放大后施加在发电机励磁系统。
模糊滑模控制器结构如图2所示。

图2 模糊滑模控制器结构图
2.1滑模变结构控制器的设计
为了适应发电机励磁系统较强的非线性,采用具有良好鲁棒性的滑模控制方法,以发电机机端电压的误差及其积分项作为系统的状态变量:
(4)
式中:U0为发电机参考电压;U为发电机机端电压。
结合式(1),并对式(4)求导数,可得:
(5)

本文在常规滑模面的基础上加入状态量的积分量,可以得到积分滑模面为:
s=e1+ce2
(6)
选取积分初始值I0为:

(7)
式中:x0为x1的初始状态;I0为积分初始值;c为积分常数,c>0。
对式(6)求导数,可得:
(8)
为使系统的动态品质更佳,采用指数趋近律来设计控制器,其表达式为:

(9)
式中:ζ>0;k>0。
系统采用等效控制法来减小切换控制量的幅值,其滑模控制量为:
u=ueq+uz
(10)
式中:u为滑模控制相;ueq为滑模等效控制部分;uz为滑模切换控制部分。
系统在s=0时所需要的控制量就是滑模等效控制部分ueq,用来控制发电机励磁控制系统的励磁电压,则:

(11)
为了使系统状态趋向滑模面,滑模切换控制部分uz通过高频切换控制,可以保证状态变量运行到滑模面,并沿滑模面滑动,直到平衡点,且使系统具有很强的鲁棒性。其表达式为:
uz=-ζsgn(s)
(12)
由此可得:

(13)
通过Lyapunov函数,证明系统的稳定性。

将式(9)代入式(13),可得:

(14)

2.2模糊控制器的设计
模糊控制器的输入是发电机机端电压的误差及其变化率,作模糊化处理后通过模糊推理和反模糊化得到模糊控制器的输出。本设计通过模糊控制器实现滑模切换控制,削弱了滑模控制中的抖振,同时提高了系统的稳定性,动态品质较高。系统输入、输出模糊集定义如下[11]:
s={NBNMNSZOPSPMPB}

uz={NBNMNSZOPSPMPB}
①模糊规则和模糊推理。
模糊控制规则如表1所示[12]。
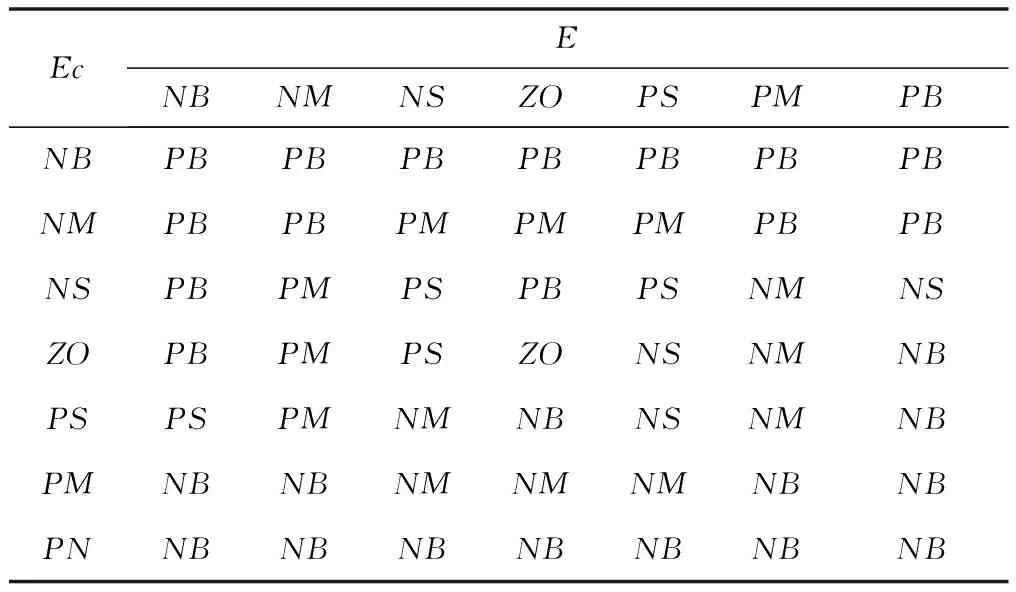
表1 模糊控制规则
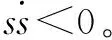
模糊推理采用双输入单输出的控制结构,定义如下:
②反模糊化。
根据以上推理规则,采用重心法,可得去模糊化后模糊控制器的输出为:
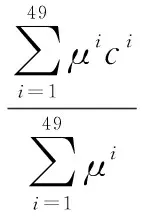
(15)
式中:μi为第i条规则的隶属度;ci为第i条规则输出的中心点。
3 仿真研究
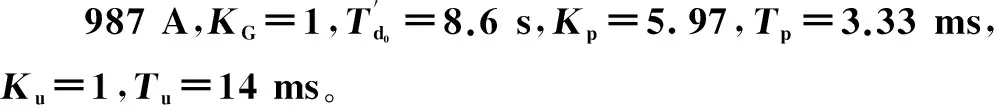
针对系统受到3%阶跃扰动先下后上的情况和线路三相短路延迟切除的情况进行仿真,仿真结果对比如图3所示。
由图3可以看出:单纯地采用滑模变结构控制时,系统超调量较大且稳定后存在抖振现象;而采用模糊滑模变结构控制算法,系统响应速度加快,鲁棒性较强,且可以很好地抑制抖振。
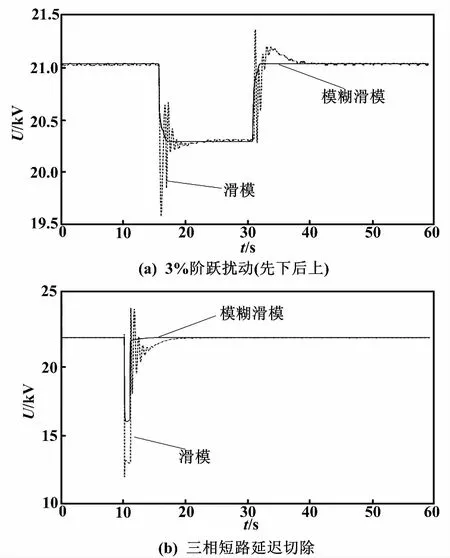
图3 仿真结果对比图
4 结束语
本文提出一种模糊滑模控制方法。为了提高系统的响应速度,在滑模趋近运动段采用指数趋近律,并采用模糊控制实现对滑模切换的时机和切换量的控制,使系统的抖振及鲁棒性得以改善。与其他进化算法相比,模糊滑模控制算法无需精确的系统数学模型,鲁棒性好、响应速度快、自适应能力强,特别适用于发电机励磁系统。
以贵州某电厂发电机组参数为基础进行仿真。仿真结果对比证明了模糊滑模控制算法应用于同步发电机非线性励磁控制系统的有效性。模糊滑模作为一种有效的非线性励磁控制新方法,对开展同步发电机励磁系统仿真研究与设计,具有重要的应用价值和广阔的工程应用前景。
[1] 汤辉.复合励磁永磁同步发电机励磁控制策略的研究[D].长沙:湖南大学,2013.
[2]JOHANM,SJOERDWH.Ridethroughofwindturbineswithdoubly-fedinductiongeneratorduringavoltagedip[J].IEEETransactiononEnergyConversion,2005,20(1):435-441.
[3]EKANAYAKEJB,HOLDSWORTHL,WUX,etal.Dynamicmodelingofdoublyfedinductiongeneratorwindturbines[J].IEEETransactionsonPowerSystems,2003,18(2):803-809.
[4] 徐果薇.同步发电机励磁系统的智能控制方法研究[D].重庆:重庆交通大学,2014.
[5] 孙慧芳,朱翔,王海.汽车线控转向系统的模糊滑模控制研究[J].自动化仪表,2017,38(1):29-33.
[6]MULLERS,DEICKEM,DONCKERRW.Doublyfedinductiongeneratorsystemsforwindturbines[J].IEEEIndustryApplicationMagazine,2002,8(3):26-33.
[7] 杨静.发电机并联运行仿真及励磁系统的自适应控制研究[D].南京:南京邮电大学,2015.
[8] 杨苹,周少雄,胡斌,等.双馈风力发电机系统的自抗扰神经网络的励磁控制[J].控制理论与应用,2012(2):251-256.
[9] 程启明,程尹曼,薛阳,等.同步发电机励磁控制方法的发展与展望[J].电力自动化设备,2012(5):108-117.
[10]徐敏,林辉.基于迭代学习控制理论的励磁控制器设计[J].电力自动化设备,2006,26(3):69-72.
[11]王春梅,李红,张丽琼,等.基于饱和函数的永磁同步直线电机模糊速度控制系统的研究[J].煤矿机械,2012,33(11):71-73.
[12]蔡满军,侯威,王琳,等.永磁同步直线电机基于推力观测器的模糊滑模控制[J].微电机,2014,47(5):50-53.
StudyofFuzzySlidingModeControlforSynchronousGeneratorNonlinearExcitationSystem
CHEN Jin1,ZHANG Xiao2,WANG Ping1,MIN Guojun2,LIANG Ling1,CHEN Feng2
(1.Power Grid Dispatching Control Center of Gui Zhou Power Grid,Guiyang550002,China;2.Grid Application Department of NR Engineering Technology Co.,Ltd.,Nanjing211102,China)
Synchronous generator excitation system is a complex control system with time-varying,multi-time-delay and highly nonlinear.The reliability of its operation directly affects the stability of the whole power system.Therefore,it is important to control the excitation system effectively.In order to solve this problem,a fuzzy sliding mode compound control strategy is proposed to meet the dynamic and static performance requirements of the generator excitation system.Sliding mode control can effectively solve the robustness problem of generator excitation control and ensure the global asymptotic stability of the system,with the advantages of its invariance of disturbance and perturbation.At the same time,the method of exponential convergence law can be used to make the system reach the switching surface quickly in the approaching motion section.Fuzzy control applied to the excitation control can mimic people’s experience to carry out expert control of complex objects,provide better damping effect,reduce the sliding mode movement of the buffeting phenomenon, and improve the dynamic quality under the disturbance.MATLAB is used to simulate to verify the effect of the algorithm.The results show that,compared with the simple sliding mode control,the proposed algorithm can improve the response speed of the generator excitation system,enhance the robustness and improve the stability of power system effectively.
Synchronous generator; Nonlinear; Excitation system; Fuzzy control; Sliding mode control; Compound control; Self-adaption; MATLAB
if (E is A) and (Ecis B) then (k is C)
TH113.1;TP273+.3
10.16086/j.cnki.issn1000-0380.201710002
修改稿收到日期:2017-06-06
国家自然科学基金资助项目(51505213)
陈金(1980—),女,硕士,高级工程师,主要从事电力调度自动化技术的研究。E-mailzdhxlj@njit.edu.cn。
