泰勒公式的应用探讨

王 丹

（吉林建筑大学城建学院，吉林 长春 130014）

泰勒公式的应用探讨

王 丹

（吉林建筑大学城建学院，吉林 长春 130014）

泰勒公式是高等数学中的一个重要定理,它可将一些复杂的函数近似表示为简单的多项式函数.泰勒公式是研究函数的一个重要工具,在函数极限、导数的求解,方程根的存在性、不等式证明及近似计算中有着重要应用.本文对此进行了分析探讨，以供参考.

泰勒公式；极限；高阶导数

泰勒公式是将一个在x=x0处具有n阶导数的函数f(x)利用关于(x=x0)的n次多项式来逼近函数的公式.泰勒公式的将指数函数、对数函数、三角函数及反三角函数等一些复杂的函数近似地表示为最为简单的多项式函数来研究.是高等数学中的一个重要内容,在函数极限、导数的求解,方程根的存在性、不等式证明及近似计算中有着重要应用.

1 利用泰勒公式求极限

极限是高等数学中的重要基础概念,连续、微分、积分等基本概念都是建立在极限概念的基础之上.未定式极限是极限计算中一种常见形式,等价无穷小代换及洛必达法则是学生们常选用的两个方法.但两种方法都具有局限性，等价无穷小代换只能用于乘、除因子,作为加、减项的无穷小量不能随意用其等价无穷小替换.应用洛必达法则是有些函数求导比较繁琐甚至需要多次应用洛必达法则,计算量很大.此时,利用泰勒公式计算是一种更有效的方法.

解 当x→0时,由于

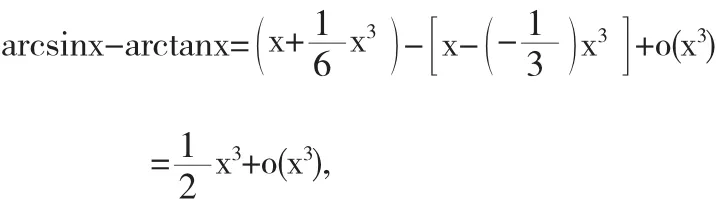
所以

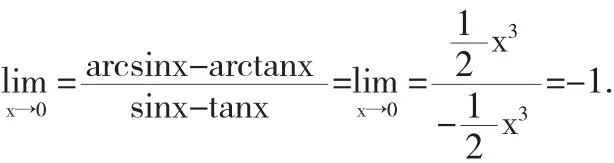
该题利用带有佩亚诺型余项的麦克劳林公式（泰勒公式在x=0处的展开式）,如用洛必达法则求该函数极限,需要用三次,且求导越来越复杂.由此例可看出,泰勒公式是计算函数极限的一个重要、有效的工具.

2 利用泰勒公式求高阶导数

写出函数y=f(x)泰勒展开式,再比较系数是求高阶导数f(n)(x0)的常用方法,具体步骤为：

⑵题目给出一个具体的无穷阶可导函数y=f(x)通过泰勒公式或麦克劳林公式展开成幂级数;

⑶根据函数展开式的唯一性,比较系数,即可求得f(n)(x0)或者f(n)(0).

例2 求函数y=ln(1-2x)在x=0处的n阶导数f(n)(0).

解 ⑴由于y=ln(1-2x)无穷阶可导,则将其展开为

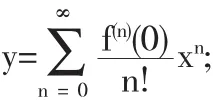
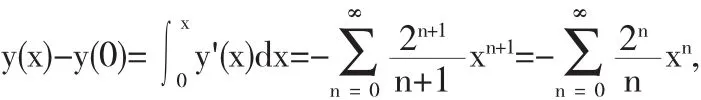
因此y(n)(0)=-2n(n-1)!

例3 设函数c,且f"'(0)=1,求a的值.

此题若直接求,运算量非常大.泰勒公式是求函数阶导数的一个基本方法.

3 利用泰勒公式证明方程根的存在

证明根的存在性的常用方法是连续函数的零点定理和罗尔定理,但一般地,若题设条件具有二阶或二阶以上的导数,应先考虑泰勒公式.

例4 设f(x)在[-1,1]区间上三次可微,证明存在实数)使得

令x分别为1,-1,得

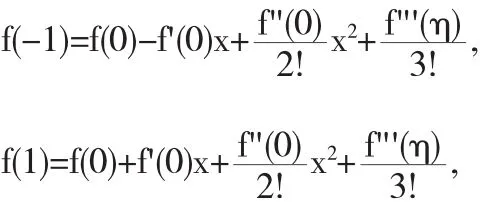
其中 η1∈(-1,0),η2∈(0,1).上述两式相减得

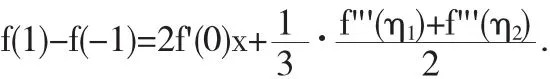
设 f"'(x)在[η1,η2]上的最大值、最小值分别为 M,m,则

根据介值定理,存在 ξ∈(η1,η2)⊂(-1,1),使得

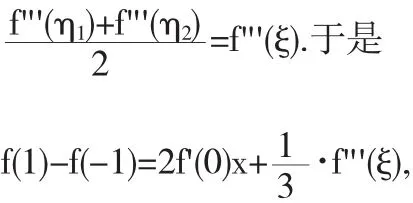
存在实数ξ∈(-1,1)使得

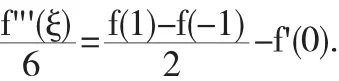
4 利用泰勒公式证明不等式

拉格朗日中值定理、泰勒公式是证明不等式的常用方法,当命题中含有f(n)(x)(n≥2)时常选用泰勒公式.

例5 证明若f(x)在[a,b]上存在二阶导数,且f'(a)=f'(b)=0,则∃ξ∈(a,b),使

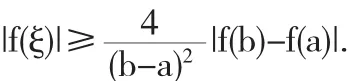
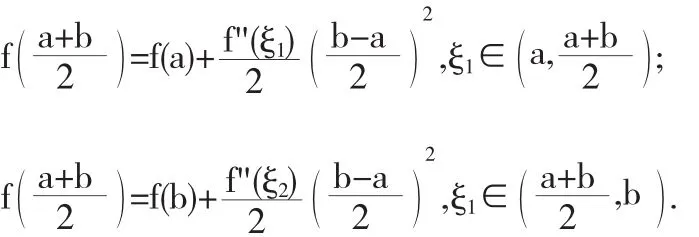
即∃ξ∈(a,b),使

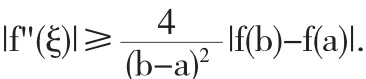
〔1〕苗文静,王昕.关于泰勒公式及其应用的思考与讨论[J].哈尔滨师范大学自然科学学报,2013,29(5)：18-21.

〔2〕王小玲.泰勒公式求极限[J].数学教学研究,2013,32(2)：55-58.

〔3〕黄先开,曹显兵.2010年考研数学经典讲义(理工类)[M].北京：中国人民大学出版社,2009.84-86.

〔4〕张宇.高等数学 18讲[M].北京：北京理工大学出版社,2013.78-79.

O172

A

1673-260X（2017）10-0001-02

2017-07-24