一维非均匀介质中Casimir Stress的收敛性
2017-11-02欧阳丹陈棋江
欧阳丹, 陈棋江, 罗 斌
(华南师范大学华南先进光电子研究院, 广州 510006)
一维非均匀介质中Casimir Stress的收敛性
欧阳丹, 陈棋江, 罗 斌*
(华南师范大学华南先进光电子研究院, 广州 510006)
基于Lifshitz理论和计算Casimir stress (σ)的规范化方法,研究一维非均匀介质中σ的收敛性. 通过对电磁场格林函数的Galerkin变分方程的证明与分析结果表明,采用Lifshitz公式理论体系及常规的规范化方法时,只要介质中某处的介电常数ε或磁导率μ的一阶导数不为零,σ在这些导数非零处为发散的. 研究结果证明了现有的规范化方法不适于计算非均匀介质,为改进现有物理模型和探索适用于非均匀介质的新方法提供了理论参考.
Casimir stress; Lifshitz理论; 非均匀介质
Keywords: Casimir stress; Lifshitz theory; inhomogeneous media
空间中存在有限的真空能量,导致2块不带电的平行板之间即使在绝对零度的情况下也存在吸引力, CASIMIR[1]提出了这种由量子涨落引起的力,即Casimir力. 通常,这种作用力由于太弱而不易被探测. 但是如果2块平板之间的间距在微米范围内,那么平板之间的Casimir力是能够被探测的[2]. 例如ALMASI等[3]设计并制造了一种新型力传感器测量大面积的Casimir力. 它不一定是吸引力,只要选取合适的相互作用材料,Casimir力也可以是排斥力,而且排斥力比吸引力更弱[4].
从理论上来阐述Casimir效应,计算Casimir力的方法主要可分为3种:模式求和法[5-6]、反射系数法[7-9]和Lifshitz理论方法[10-11]. 在计算任意数量、相互分隔的物体或色散和耗散介质之间的Casimir力时,最常用的方法是Lifshitz理论方法. Lifshitz理论体系以电磁格场林函数为基础,将电磁场张量以格林函数的形式表示,推导出Casimir stress (σ),从而进一步计算Casimir力. 尽管Lifshitz理论中涉及的计算非常复杂,但是在许多问题中,Lifshitz理论能够通过纯粹的数值计算来求解,从而使它具有广泛的适用性,并且已被成功运用于实验中. 然而,Lifshitz理论在计算求解非均匀介质[12-13]的过程中遇到了发散的问题. 文献[12]提出的规范化方法会导致非均匀介质内部任意处的σ无穷大,从而导致Casimir力无法计算,但是并没有给出严格的理论证明. 提出的新的规范化方法也未能从本质上解决σ的发散问题,其理论基础的正确性还有待验证.
σ在非均匀介质中发散[9,12-13],但没有从理论上明确指出σ收敛性的规律. 一般认为σ与真空中Casimir力的计算不相关. 然而在实际中,实验环境通常是物体被浸入到流体中,在这种情况下,Casimir力必须通过σ来计算. 因此,弄清楚σ收敛性的规律非常重要.
本文根据Lifshitz理论,在现有的σ规范化方法的基础上,对其做进一步数学演绎,得到σ的计算公式,通过研究电磁场格林函数及其Galerkin变分方程,总结了在现有公式体系下σ的发散规律.
1 计算方法
在一维非均匀介质(y和z方向平移不变)中,计算3×3矩阵的σ时只需计算其中的1个元素σxx.以Lifshitz理论为基础进行推导[14]
(1)
(2)
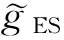
中的一个元素;上标E、M分别表示电场、磁场. 由式(1)和式(2)之和可得到σxx(x′)的计算公式. 本文在此基础上,将其在y-z平面进行二维傅里叶变换为
(3)
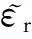
gES|MS(iκ;x′,x′,0)]dκ,
(4)
其中,
gES|MS(iκ;x,x′,ρ)=gE|M(iκ;x,x′,ρ)-g0(iκ;r,r′),
(5)
g0(iκ;r,r′):=

(6)
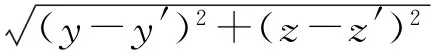
(7)
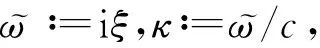
(8)
(9)

(10)
微分方程(9)可以转化为如下的标准形式:
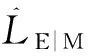
(11)
其中,
(12)
为了便于后续的推导,将式(12)进一步变为:
(13)

(14)
其中,
(15)
根据式(3)和式(4)可以得到一维非均匀介质中σ的计算公式:
(16)
其中,
(17)
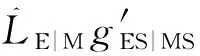
(18)

(19)
其中,
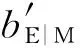
(20)
(21)

(22)
其中,φ(r)是满足如下条件的试函数:φ(r)在3空间内有限并连续,且存在大于0的距离d,使得当|r|≥d时,φ(r)恒等于0,并且φ(r)在Vn任何地方都可导,并且,
(23)

(24)


(25)
是有限的,但是式(22)中等号右边的
(26)
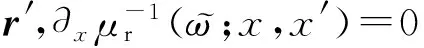
2 程序验证
为了验证非均匀介质中σ是发散的,本文采用有限元法(FEM)编程计算了2块相距d=xR-xL的无限大金属板之间中点处的σxx. 当两金属板间的介质分别为均匀介质(图1A)和线性非均匀介质(图1B)时,两金属板中点x′=(xL+xR)/2处的σ随网格划分数的变化情况见图2. 所有介质的相对磁导率μr均为1.
有限元法将待求解的区域划分为细小的网格区域,以近似计算各点的数值解,网格划分越精细,结果越接近真实值. 容易看出,当介质为均匀介质时(图2A),随着网格划分数的增加,σxx趋于有限值. 而当介质为非均匀介质时(图2B),σxx随着网格划分数增加而无限增大,说明均匀介质中的σxx收敛,而非均匀介质中的σxx是发散的.

图1 不同介质中相对介电常数εr的分布
Figure 1 Distribution of relative dielectric constant in different medias
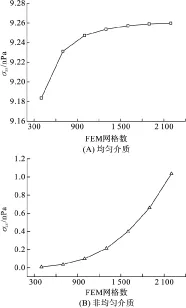
图2 不同介质中两金属板之间中点x′处σxx随FEM网格数的变化
Figure 2 Changes ofσxxat the meddle pointx′of two metal sheets in different media
3 结论
针对一维非均匀介质中Casimir stress (σ)的发散问题,基于Lifshitz理论,在现有的σ规范化方法基础上,本文对其推导演绎,得到一维非均匀介质中σ的计算公式. 通过证明和分析电磁场格林函数及其Galerkin变分方程得到以下结论:在现有基于Lifshitz理论及其标准规范化方法体系下,在介质的介电常数ε或磁导率μ对x的一阶导数不为零的地方,σ必然发散,从而无法通过其计算非均匀介质中的Casimir力. 这说明了现有的规范化方法模型对非均匀介质是不适用的. 后续可改进现有物理模型,并寻找新的适用于非均匀介质的规范化方法.
[1] CASIMIR H.On the attraction between two perfectly conducting plates[J]. Frontiers of Physics,1989,51:793-795.
[2] MOHIDEEN U,ROY A. Precision measurement of the Casimir force from 0.1 to 0.9 microns[J]. Physical Review Letters,1998,81(21):4549-4552.
[3] ALMASI A,BRAX P,IANNUZZI D,et al. Force sensor for chameleon and Casimir force experiments with parallel-plate configuration[J]. Physical Review D,2015,91:102002.
[4] MUNDAY J N,CAPASSO F,PARSEGIAN V A. Mea-sured long-range repulsive Casimir-Lifshitz forces[J]. Nature,2009,457(7226):170-173.
[5] GOTO S,HALE A C,TUCKER R W,et al. Numerical regularization of electromagnetic quantum fluctuations in inhomogeneous dielectric media[J]. Physics,2012,85(3):484-487.
[6] BAO F,LUO B,HE S. First-order correction to the Casimir force within an inhomogeneous medium[J]. Physical Review A,2015,91(6):063810.
[7] GENET C,LAMBRECHT A,REYNAUD S. Casimir force and the quantum theory of lossy optical cavities [J]. Physical Review A,2003,67(4):043811.
[8] ELLINGSEN S A,BREVIK I. Casimir force on real materials-the slab and cavity geometry[J]. Journal of Physics A:Mathematical & Theoretical,2007,40(13):3643-3664.
[9] SIMPSON W M R,HORSLEY S A R,LEONHARDT U. Divergence of Casimir stress in inhomogeneous media[J]. Physical Review A,2013,87(4):61-65.
[10] LIFSHITZ E M. The theory of molecular attractive forces between solids [J]. Soviet Physics,1956,2(1):73-83.
[11] DZYALOSHINSKII I E,LIFSHITZ E M,PITAEVSKII L P. The general theory of van der Waals forces [J]. Advances in Physics,1961,10(38):165-209.
[12] PHILBIN T G,XIONG C,LEONHARDT U. Casimir stress in an inhomogeneous medium [J]. Annals of Physics.2010,325(3):579-595.
[13] XIONG C,KELSEY T W,LINTON S A,et al. Casimir forces for inhomogeneous planar media [J]. Journal of Physics:Conference Series,2013,410(1):012165.
[14] LEONHARDT U. Essentialquantum optics:from quantum measurements to black holes [M]. Cambridge:Cambridge University Press,2010:231-249.
Convergence of Casimir Stress in One-Dimensional Inhomogeneous Media
OUYANG Dan, CHEN Qijiang, LUO Bin*
(South China Academy of Advanced Optoelectronics, South China Normal University, Guangzhou 510006, China)
Based on the Lifshitz theory and the regularization method for the calculation of Casimir stress (σ), the convergence ofσin one-dimensional inhomogeneous media is studied. By deriving and analyzing the Galerkin variational equation of Green’s function of electromagnetic field,σis divergent in the nonzero derivative when the Lifshitz formulism and standard regularization method are applied either the derivative of permittivityεor the derivative of permeabilityμis nonzero somewhere in the media. The results show that the existing standard regularization is not applicable to inhomogeneous media, and provide a theoretical reference for the improvement of the current physical model and the exploration of new regularization applicable to inhomogeneous media.
2016-02-22 《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n
广东省引进创新团队计划项目(201001D0104799318)
*通讯作者:罗斌,讲师,Email:bin.luo@coer-scnu.org.
O431.2
A
1000-5463(2017)05-0022-04
【中文责编:谭春林 英文审校:肖菁】
