被动段扰动引力对闭路制导的影响及补偿方法研究

王宗强, 吴燕生, 张 兵, 常晓华

（1. 北京宇航系统工程研究所，北京，100076；2. 中国航天科技集团公司，北京，100048）

被动段扰动引力对闭路制导的影响及补偿方法研究

王宗强1, 吴燕生2, 张 兵1, 常晓华1

（1. 北京宇航系统工程研究所，北京，100076；2. 中国航天科技集团公司，北京，100048）

针对被动段扰动引力对弹道式飞行器落点精度的影响问题，提出闭路制导对被动段扰动引力的实时补偿方法。建立动坐标系下自由段运动模型，导出由被动段摄动量计算落点位置的计算公式；分析扰动引力对闭路制导精度的影响机理，得出被动段扰动引力对闭路制导的影响仅与关机点位置相关的结论；进一步利用均匀设计理论，将被动段摄动量拟合为关机点位置偏差的函数，提出将摄动量作为扰动引力修正项引入闭路制导回路的实时补偿方法。仿真结果表明：验证补偿后落点偏差小于5 m，满足制导精度要求。

扰动引力；被动段；闭路制导；均匀设计；补偿方法

0 引 言

弹道式飞行器广泛采用闭路制导方法，利用需要速度的概念将飞行器当前位置和目标位置联系起来。需要速度指若飞行器在当前位置处关机，经被动段飞行后到达目标点应具有的速度[1]。在正常引力场作用下，以需要速度关机后飞行器将准确到达目标，但实际被动段飞行过程中飞行器受到扰动引力的影响，必然会造成落点偏差。由于弹道式飞行器的被动段飞行仅受引力与再入气动的作用，无主动控制力，若要提高考虑扰动引力时的精度，可在主动段需要速度计算中引入扰动引力补偿项进行补偿[2]。

针对被动段飞行特性，一些文献研究了球谐函数法计算被动段扰动引力的合理截断阶数，对远程弹道式飞行器受被动段扰动引力影响下的落点偏差进行了定量分析[3，4]。但以上研究都是在发射系下建立自由段运动方程，难以剖析扰动引力对被动段运动的影响机理。郑伟等对考虑扰动引力场时的显式制导方法进行初步探讨，提出结合球谐函数换极法[5]对扰动引力的影响进行实时补偿的方案[2]，但计算速度仍然难以满足实时计算的需要[6]。

本文不考虑再入气动的影响，研究被动段扰动引力对闭路制导的影响机理，提出相应补偿方法：a）在动坐标系下建立自由段运动模型，将自由段受摄动项影响的位置偏差分解为射程角偏差、飞行时间偏差及侧向角偏差3个摄动量，导出由摄动量计算落点经纬度的公式；b）分析被动段扰动引力对闭路制导的影响，得出与扰动引力影响直接相关的为闭路制导关机点位置的结论；c）根据均匀设计理论，将扰动引力对摄动量的影响拟合为关机点位置偏差的函数，给出预测扰动引力引起落点偏差的方法；d）将摄动量作为扰动引力修正项引入虚拟目标求解中，实现对扰动引力的实时补偿，并通过仿真验证补偿效果满足制导精度要求。

1 数学模型

1.1 自由段运动模型

定义动坐标系如图1所示。

图1中，由自由飞行起始点K处的 rK与 vKA构成的平面称为标准轨道面，在摄动力作用下飞行器将偏离标准轨道面。O与 P1重合，r轴在标准轨道面内由地心OE指向O； 轴在标准轨道面内且垂直于r轴；z轴垂直于标准轨道面，与r轴、β轴构成右手系。飞行器在任一点P处的地心矢径 rP可写成两个分量r和z的和，即：

式中re，βe，ze为动坐标系中沿坐标轴方向的单位矢量，进一步可将飞行器自由飞行运动分解为在标准轨道面内的分运动和垂直于标准轨道面的分运动。

根据理论力学知识，经过推导可以得到在动坐标系下以射程角 为自变量的运动微分方程组[7]：

式中 为地球引力常数； 为侧向角偏差，且η= a rctan(z r)； Vr为径向速度；Vβ为周向速度； Vz为侧向速度；t为飞行时间；δar，δaβ，δaz分别为摄动加速度在动坐标系的分量。

由式（2）可得自由段运动给定地心距处的运动状态。与标准椭圆轨道相比，得到与落点位置计算有关的3个摄动量：射程角偏差βΔ、飞行时间偏差tΔ及侧向角偏差 。

1.2 落点经纬度计算

假设在旋转地球上有一与地球表面重合但不随地球旋转的惯性球壳，如图2所示，椭圆弹道在惯性球壳上的落点为 TA。已知关机点处地心纬度为φ，椭圆弹道在K′K点的方位角为射程角为 ，飞行时间为惯性球壳上实际落点为 CA，地心纬度为φc，对应摄动量偏差为Δβ，Δt， 。

椭圆弹道与实际弹道间的方位角差为AαΔ，由球面三角公式可得：

则，实际轨道在K′处的方位角为

K′CA为实际轨道射程角，记为β*，

则，

由上述公式可得到实际落点纬度φc及落点与关机点绝对经差，则相对经差为

式中eω为地球自转角速度。

1.3 需要速度迭代计算

根据定义，需要速度实际上是要求根据实际目标位置实时考虑各种摄动因素求取的。为简化需要速度计算提出虚拟目标的概念，以虚拟目标为边界条件，给定关机点速度倾角约束，按照椭圆轨道理论计算得到需要速度[8]，以此速度关机经被动段飞行后恰好到达实际目标，虚拟目标按照文献[9]的方法确定。

2 扰动引力对制导精度的影响分析

不考虑扰动引力时，采用闭路制导方法可以获得满足精度要求的需要速度，但实际飞行中，由于扰动引力的存在，必然会使落点偏离目标点，造成落点偏差。采用球谐函数法[10]可得到飞行器所受扰动引力在北天东坐标系下的投影：

由坐标转换关系可得扰动引力在动坐标系下分量为

将扰动引力项并入摄动加速度中，可以得到扰动引力引起的位置摄动量，进而计算出落点偏差。被动段扰动引力对精度的影响分析如图 3所示。扰动引力对落点偏差的影响与关机点的位置和速度有关，而按照闭路制导的要求，关机点的速度应该等于该点需要速度，而且当目标位置给定后，飞行过程中任一点的需要速度仅与该点的位置有关，因此对于采用闭路制导方法的弹道式飞行器而言，被动段扰动引力的影响仅由关机点位置决定。

对于标准弹道而言，只需针对标准关机点位置进行一次计算即可得到扰动引力对摄动量的影响。但实际飞行中，由于各种干扰因素的影响，飞行器的实际关机位置与标准关机点有一定的偏差，导致扰动引力作用下的摄动量发生变化，若仍以标准关机点位置下的摄动量计算，则对落点位置的预测值将产生偏差。

若在飞行过程中计算被动段扰动引力，实时计算量过大。本文采用均匀设计方法建模，将扰动引力引起的摄动量拟合为关机点位置偏差的函数，事先装订到飞行器上，利用该拟合函数在飞行过程中实时计算摄动量，无需实时计算被动段扰动引力，可满足计算快速性的要求。

3 均匀试验设计在落点偏差预测中的应用

3.1 方法

均匀设计方法是一种考虑试验点在试验范围内均匀散布的试验设计方法，其数学原理是数论中的一致分布理论[11]。针对本文研究内容，均匀设计步骤为：a）确定影响因素及水平；b）选择均匀设计表，制作试验方案表；c) 利用仿真程序计算摄动量；d）试验结果统计分析，求摄动量的最优预报公式。

3.2 仿真试验条件

通过第 2节的分析可知，闭路制导中与被动段扰动引力的影响相关的因素为关机点位置偏差，令xi(i =1, 2, 3)为x，y，z方向的位置偏差。各因素取值范围取为：

x方向偏差 ΔxK：-50 km ≤ x1≤ 50 km；

y方向偏差 ΔyK：-40 km ≤ x2≤ 40 km；

z方向偏差 ΔzK：-10 km ≤ x3≤ 10 km；

水平数统一取为11。选定均匀设计表U11(113)，如表1所示。按照表1进行11次不同条件下的仿真计算，得到扰动引力引起的摄动量Δβδ，Δtδ和ηδ如表2所示。

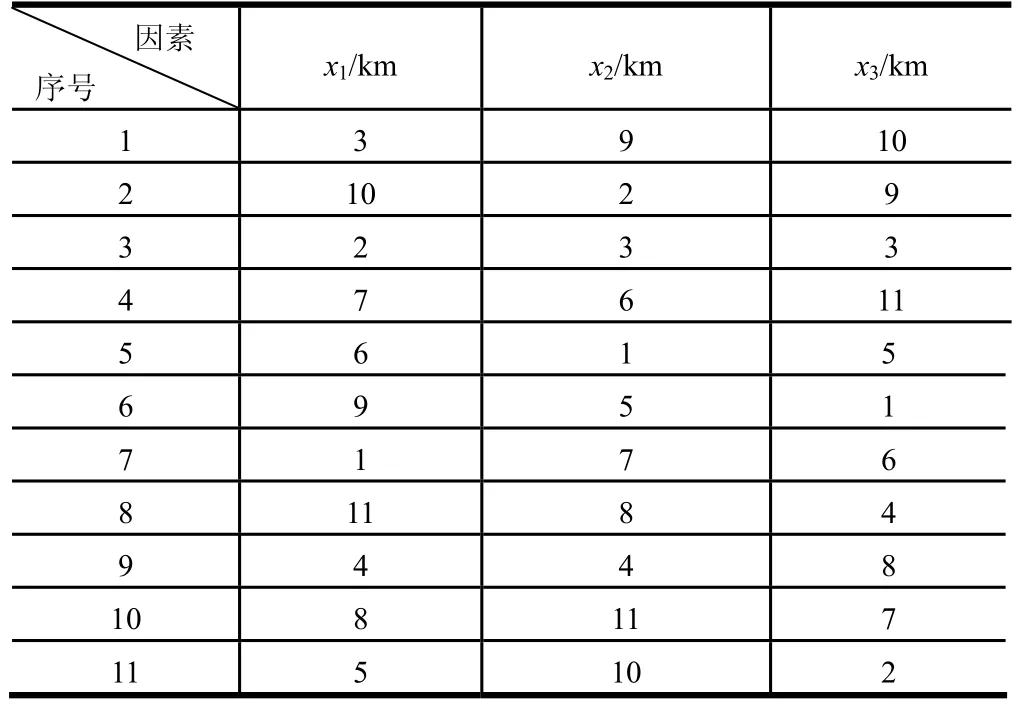
表1 U11(113)均匀设计表

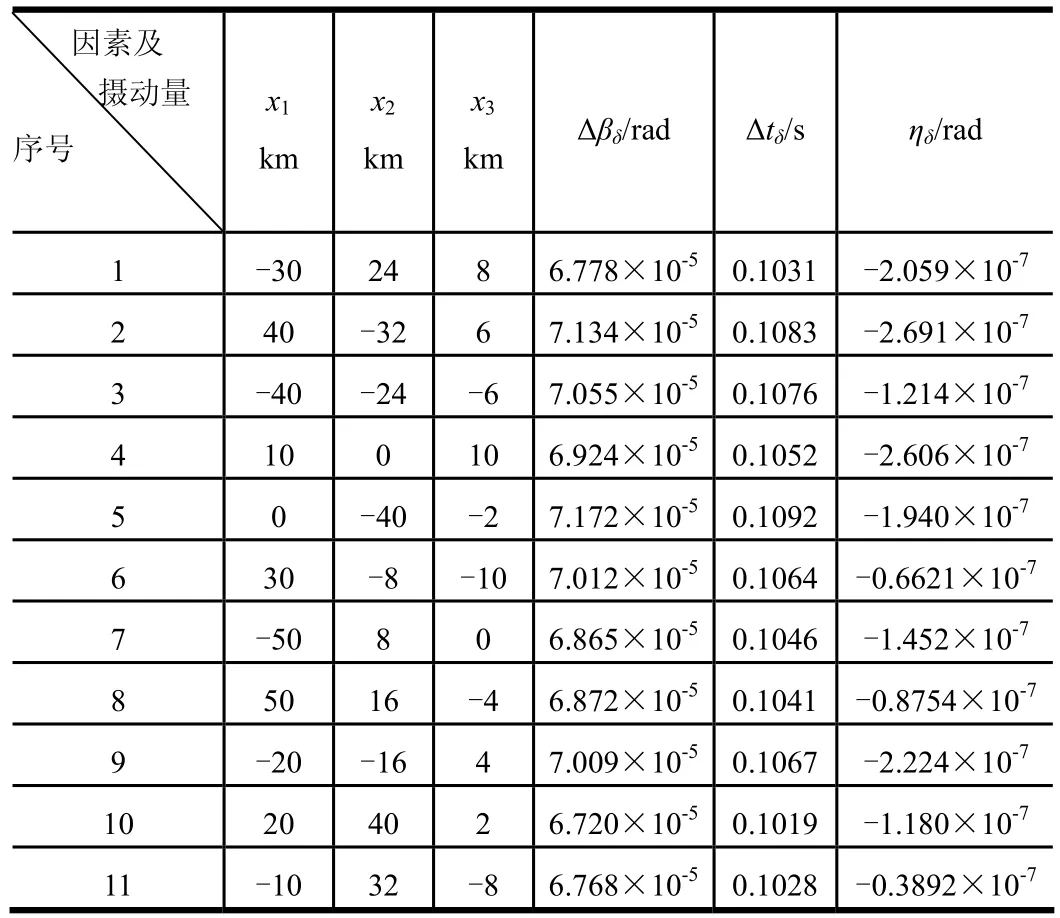
表2 均匀设计仿真结果

3.3 试验结果回归分析

为了得到影响因素对于摄动量影响的数学关系式，还需利用回归分析方法进行数据处理。本文按照二次多元逐步回归模型来筛选变量，取Fin= Fout= 2，F检验显著性水平为0.01。以Δβδ为例，得到回归方程为

回归分析结果如表3所示，全相关系数R2= 1.00，残差标准差s = 0.0013，查表可知F0.01(6, 4) = 15.2，满足F ＞ Fα(s, n-s-1)，因此回归方程十分显著。

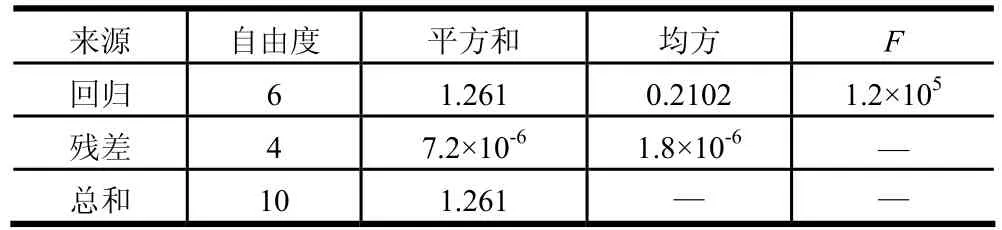
表3 方差分析表

同理可得到Δtδ与ηδ的回归方程：

得到关于摄动量的 3个回归方程后，为评估回归模型精度，针对几个典型偏差条件对落点偏差进行预测，与实际落点偏差的比较如表4所示。由表4可知，关机点偏差在预定范围内时落点偏差预测精度优于0.3 m，由均匀试验设计方法得到的回归模型精度较高，回归模型可信。

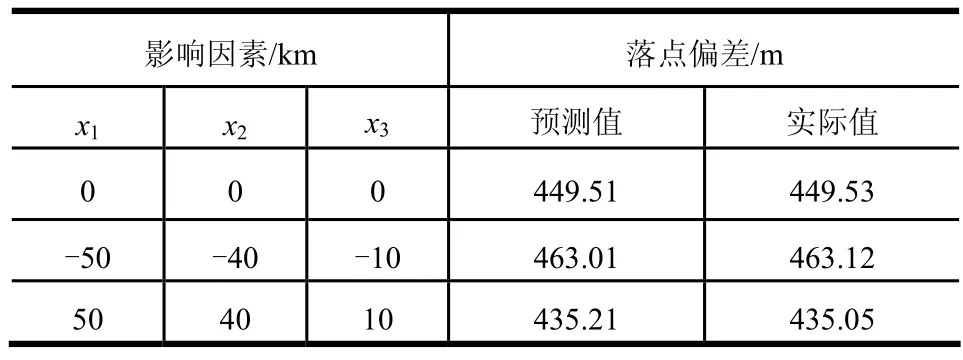
表4 落点偏差预测值与实际值比较

4 闭路制导中对扰动引力的补偿

4.1 考虑扰动引力时虚拟目标的修正

对于采用闭路制导方法的弹道式飞行器，可对虚拟目标进行进一步修正，以补偿被动段扰动引力的影响。将扰动引力引起的射程角偏差、飞行时间偏差与侧向角偏差以补偿项的形式引入实时落点预测及虚拟目标计算，进而得到考虑被动段扰动引力作用下的需要速度，实现对扰动引力的补偿。为评估该方案对扰动引力的补偿效果，先通过迭代得到考虑地球扁率的需要速度，再对扰动引力的影响进行一次补偿，此时的落点偏差即为对扰动引力的补偿精度。假设某时刻tK，飞行器位置参数为，实时计算需要速度的步骤如下：

a）以实际目标点(或装订数值)为虚拟目标点，计算需要速度R；

c）由当前位置与标准点位置的差计算扰动引力引起摄动量δβΔ,tδΔ,δη；

d）预测被动段扰动引力作用下的实时落点位置，对虚拟目标点进行一次修正；

e）根据修正后的虚拟目标计算需要速度Rv。

4.2 补偿效果仿真分析

对于航程大于10 000 km的弹道式飞行器，当关机点无位置偏差时，按照上述补偿步骤，得到 3个需要速度，如表5所示。Rxv,Ryv,Rzv为需要速度在3个方向的分量，补偿后落点纵向偏差为2.54 m，横向偏差为4.32 m，补偿残差约占扰动引力影响的1%，满足制导精度要求。

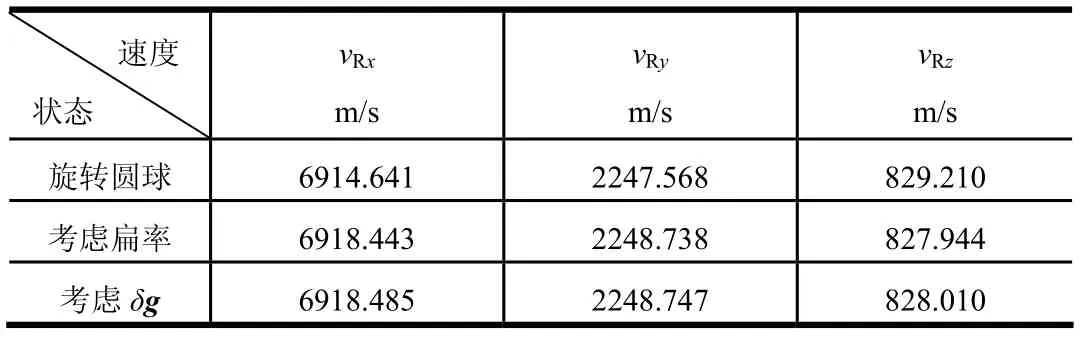
表5 3个状态下的需要速度

针对关机点出现位置偏差的情况，对补偿方法做有效性分析。将关机点位置偏差在预定范围内进行随机选取并进行500次模拟打靶，图4给出了补偿后的落点偏差。对仿真数据进行统计分析，补偿后的纵向偏差LΔ均值为2.54 m，标准差为0.015，横向偏差HΔ均值为4.32 m，标准差为0.051，对扰动引力进行实时补偿的方法误差小于5 m。且该方法只需利用拟合函数即可对扰动引力进行实时补偿，满足实时计算的需要。

实际飞行中，可能会出现关机点位置偏差超出第3.2节中选定范围的情况，进一步对本文提出的补偿方法做适应性分析。图5给出两个位置偏差都为范围内极大值时，第 3个位置偏差对补偿方法残差的影响。由图5可以看出，即使关机点位置偏差超出预定范围2倍，补偿精度仍可控制在米级，说明该补偿方法具有较强的适应性。

5 结 论

针对被动段扰动引力对闭路制导影响问题，分析了扰动引力对闭路制导过程的影响机理，得出关机点位置与扰动引力的影响直接相关这一结论，在此基础上提出一种在闭路制导中对扰动引力进行实时补偿的方案。采用均匀设计及回归分析理论，将被动段扰动引力引起的摄动量拟合为关机点位置偏差的函数，并将摄动量作为扰动引力修正项引入闭路制导回路。仿真结果表明，对于航程大于10 000 km的弹道式飞行器，在引入被动段扰动引力补偿项后，实时修正的方法误差小于5 m，满足弹道式飞行器的制导精度要求。

[1] Cornelius L T. Guidance and control of aerospace vehicles[M]. New York:McGraw-Hill, 1963.

[2] 郑伟, 汤国建. 扰动引力场中弹道导弹飞行力学[M]. 北京: 国防工业出版社, 2009.

[3] 袁宇, 王明海. 扰动引力计算及其对导弹精度影响研究[J]. 弹箭与制导学报, 2006, S6: 360-362, 366.

[4] 李晓燕, 王兴涛, 李迎春. 扰动引力对洲际弹道导弹被动段的影响分析[J]. 测绘科学技术学报, 2010(2): 109-111, 115.

[5] 任萱. 扰动引力作用时自由飞行弹道计算的新方法[J]. 国防科技大学学报, 1985(2): 47-58.

[6] 谢愈, 郑伟, 汤国建. 弹道导弹全程扰动引力快速赋值方法[J]. 弹道学报, 2011(3): 18-23.

[7] 任萱. 自由飞行时摄动方程的状态转移矩阵的解析解[J]. 中国空间科学技术, 1983(1): 1-16.

[8] Battin R H. Astronautical guidance[M]. New York: McGraw-Hill, 1964.

[9] 王继平, 肖龙旭, 王安民, 等. 一种虚拟目标点的弹道迭代确定方法[J].飞行力学, 2012(6): 551-555.

[10] 刘林. 航天器轨道理论[M]. 北京: 国防工业出版社, 2000.

[11] 方开泰. 均匀设计与均匀设计表[M]. 北京: 科学出版社, 1994.

Research on Compensation Method to Gravity Anomaly in Passive Ballistic Curve on Closed Loop Guidance

Wang Zong-qiang1, Wu Yan-sheng2, Zhang Bing1, Chang Xiao-hua1
(1. Beijing Institute of Astronautical Systems Engineering, Beijing, 100076; 2. China Aerospace Science and Technology, Beijing, 100048)

For the problem that the impact of point deviation is influenced by the gravity anomaly in passive phase of the ballistic vehicle, a real-time compensation method in the process of closed loop guidance are proposed in this paper. Kinetic equations in free flight phase are formed. And equations to calculate the impact point by perturbations are derived. Research on how the gravity anomaly influences the hit precession is carried on, through which the factors related to the gravity anomaly are fetched. A polynomial function is established through Uniform Design to express the perturbations by position deviations on cutoff point. Then, a real-time compensation method is derived in closed loop guidance to improve the hit precision. Finally, a serious of simulation proves that after compensation, the impact of point deviation is less than 5m, which is sufficient to fulfill the guidance accuracy requirement.

Gravity anomaly; Passive ballistic curve; Closed loop guidance; Uniform design; Compensation method

TJ765.1

A

1004-7182(2017)05-0049-04

10.7654/j.issn.1004-7182.20170512

2016-12-05；

2017-01-12

王宗强（1993-），男，硕士研究生，主要研究方向为飞行器设计