基于无功环流的风电变流器热负荷优化控制
2017-11-01万胜前
万胜前
(鄂州职业大学电子电气工程学院,湖北 鄂州 436000)
基于无功环流的风电变流器热负荷优化控制
万胜前
(鄂州职业大学电子电气工程学院,湖北 鄂州 436000)
大容量风电变流器的设计寿命决定了其可靠性,非常关键,而变流器中功率半导体器件的结温将随着风速变化,即随变流器运行功率的变化而波动,这将增加器件的失效率,从而影响到变流器的可靠性。针对这个问题,提出了一种基于无功环流的风电变流器热负荷优化控制策略,首先以双馈风电机组作为研究对象,对其变流器转子侧和网侧的无功环流运行边界范围进行了计算,然后分析了无功环流对变流器中各个功率器件的电流和热负荷分布的影响,从而设计了将额外的无功功率注入以在风速变化时保持功率器件热稳定的优化控制方法。最后,基于Matlab/Plecs的仿真平台建立了风电机组仿真模型并进行了对比计算。结果表明,风速变化时新控制方法使变流器的功率器件最大结温波动较传统方法减小了4℃,从而验证了其有效性。
风电变流器;双馈感应发电机;无功功率;热循环;结温
近年来,由于传统能源存在的不可持续问题,新能源得到了广泛使用,尤其是风力发电增长迅猛[1-2]。随着装机容量的增长,单个风力发电机组的容量也在快速持续增加,陆基风电也逐步发展到海上风电,甚至发展到中压系统,但也存在成本高和维护性差的缺点,因此目前主流的商业化机型仍是低压系统[3-4]。而在低压风电机组中,基于双馈感应电机DFIG(doubly fed induction generator)和半功率变流器的机型得到了广泛的使用[5-6]。其研究重点集中在机组的可靠运行上,比如风电变流器的设计使用寿命常常达到20~25 a[7-10]。
对于风电变流器而言,从可靠性设计的角度,功率半导体器件是薄弱环节,相关研究表明其热性能,尤其是平均结温和结温波动对其可靠性有显著影响[11-14]。因此,风电变流器中功率半导体器件的损耗和热负荷分布对整个风电机组的可靠性有相当程度的影响[15-16]。目前已有针对风电变流器热分析的相关研究。文献[17]的研究表明,当DFIG同步工作时变流器机侧的热应力将增大。文献[18]研究了DFIG在几种不同的控制方式下对风电变流器运行生命周期的影响。文献[19-20]提出了一种改变脉冲调制PWM(pulse width modulation)策略,结合改变开关频率来实现热负荷控制,但存在改变开关暂态过程的风险。文献[21]提出了增加额外的加热装置来实现热负荷均衡,但明显增加成本,经济性较差。
本文以DFIG风电机组为研究对象,首先计算出不同工作模式下在背靠背风电变流器中最大允许无功环流,然后分析了不同无功环流下变流器的热负荷特性,最后设计了一种基于无功环流的MW级风电变流器热负荷优化控制策略,其新型控制方法无需改变功率器件的开关频率,也不需要增加加热装置,简单易于实施,研究结果为变流器设计提供了依据。
1 DFIG机组的结构和参数
双馈风电机组由于技术成熟、结构简单、成本较低等优点得到了商业上的广泛使用[5-6]。图1所示为双馈风电机组的典型结构示意图,主要由DFIG结合两电平背靠背风电变流器及升压变压器构成。变流器转子侧RSC(rotor side converter)的主要功能是将有功功率传送给电网,或从电网吸收有功功率,同时提供发电机的励磁电流;变流器网侧GSC(grid side converter)的主要功能是控制直流侧电压稳定,同时提供规定的无功功率给电网。
DFIG风电机组相关参数为:发电机额定功率Pm=2 MW,发电机无功功率范围Qs=-570~450 var,定子额定最大相电压Usm=563 V,发电机定子和转子匝比k=0.369,发电机定子电抗Ls=2.95 mH,发电机转子电抗Lr=2.97 mH,发电机绕组互感Lm=2.91 mH,变流器额定功率Pg=330 kW,变流器额定直流电压Udc=1 050 V,变流器滤波器电抗Lg=0.5 mH,变流器RSC和GSC侧开关频率fs=2 kHz,变流器功率器件额定电压1 700 V,变流器功率器件额定电流Im=1 000 A。变压器在定子侧和变流器网侧的匝比为1∶1,即额定定子电压等于额定电网电压。对于功率器件IGBT,选择额定电压为1.7 kV和额定电流为1 kA,考虑到GSC和RSC的不同电流范围,分别采用单管和双管并联设计。
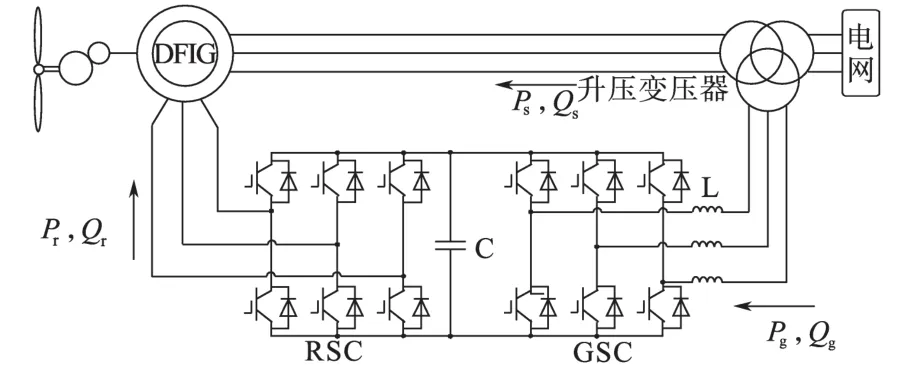
图1 DFIG风机系统的典型结构Fig.1 Typical configuration of a DFIG wind turbine system
2 无功功率对电流特性的影响
图1中绘出了有功功率和无功功率的参考方向,可以看出,无论是变流器的GSC或RSC都有控制无功功率的能力。换言之,系统可以实现内部的无功环流,而与电网没有任何额外的无功功率交换。
2.1 GSC侧的无功功率运行边界
图2为GSC单相简化等效电路图,其中Lg为滤波电感,ug为电网相电压,uC为GSC的输出电压。根据图1中功率方向的定义,可绘制施加容性无功功率的GSC矢量图如图3所示。因为DFIG在亚同步和超同步工作模式下具有相反的有功功率方向,其有功电流参考分别如图3a和图3b所示。如果引入感性无功功率,则可以将原图中的q轴电流旋转180°得到新矢量图。

图2 GSC单相简化电路图Fig.2 Simplified single-phase diagram of the GSC

图3 GSC矢量图Fig.3 Vector diagram for the GSC
变流器输出电压uC的解析表达式为

式中:Ugm,Udc分别为额定电网相电压峰值和直流母线电压;Xg为滤波器电抗在50 Hz处的值;igd,igq分别为GSC的d轴和q轴电流峰值。
从图3可以很明显地看出,DFIG无论处于何种操作模式,如果引入容性无功功率,风电变流器的输出电压幅值都将会增加。因此,式(1)也说明了在线性调制下,直流母线电压与GSC输出电压的关系。另外一个限制条件是半导体功率器件允许额定电流Im产生的,即

此外,还需考虑发电机的无功功率允许范围:

由式(1)~式(3)这3个限制构成了GSC侧的无功功率运行边界。同时,功角也是损耗评估的另一个重要指标,其特征也在图3中绘出了。
2.2 RSC侧的无功功率运行边界
若忽略定子和转子电阻,稳态运行时DFIG的等效电路如图4所示。
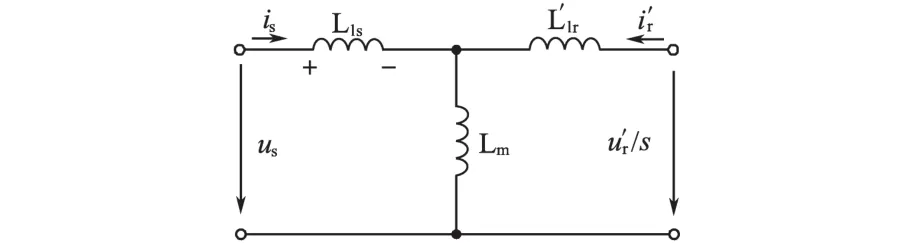
图4 稳态运行时DFIG的等效电路Fig.4 Equivalent DFIG circuit diagram in steady-state operation
图4 中,转子侧参数已经通过定转子绕组匝比k转换到定子侧,旋转坐标变换以后,在d-q坐标系下的转子电流和、转子电压和,与定子电压电流之间的关系式为
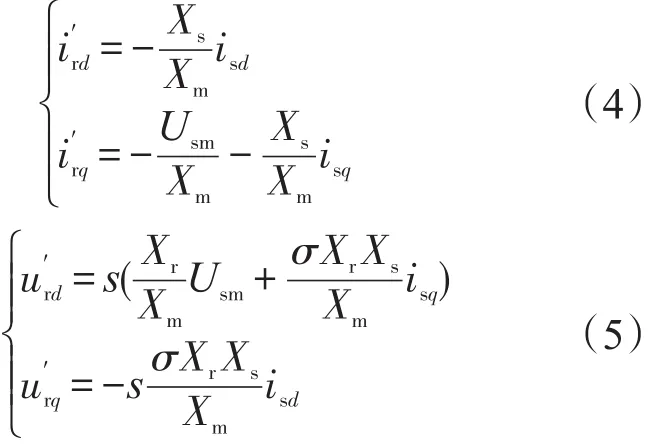
式中:s为转子滑差;σ为感应电机漏磁系数;Usm为电机定子相电压峰值;Xs,Xr,Xm分别为在50 Hz频率点的定子感抗、转子感抗和互感抗;isd,isq分别为RSC的d,q轴峰值电流。
如果RSC也注入无功功率,则其在亚同步和超同步工作模式下的矢量图分别如图5a和图5b所示。
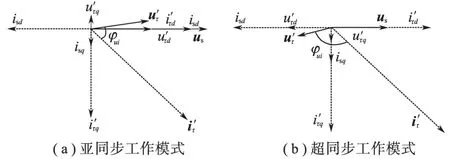
图5 RSC矢量图Fig.5 Vector diagram for the RSC
和GSC类似,在线性调制下,主要由直流电压、发电机容量以及功率器件额定参数构成了RSC的无功功率运行边界,具体的表达式如下:
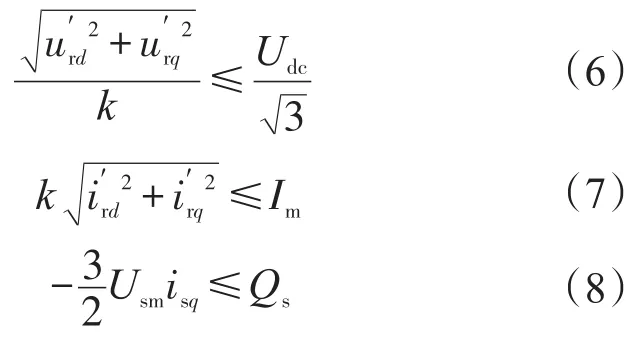
2.3 风电变流器的电流运行特征
电流幅值和功率因数角是背靠背风电变流器功率器件负荷相关的2个指标,因此,有必要研究在无功功率允许运行范围内对电流特性的影响。
如果选择风速5.9 m/s和10.1 m/s作为亚同步和超同步2种工作模式下的典型运行风速,则通过计算可以得到GSC和RSC的无功功率的运行范围,如表1所示。
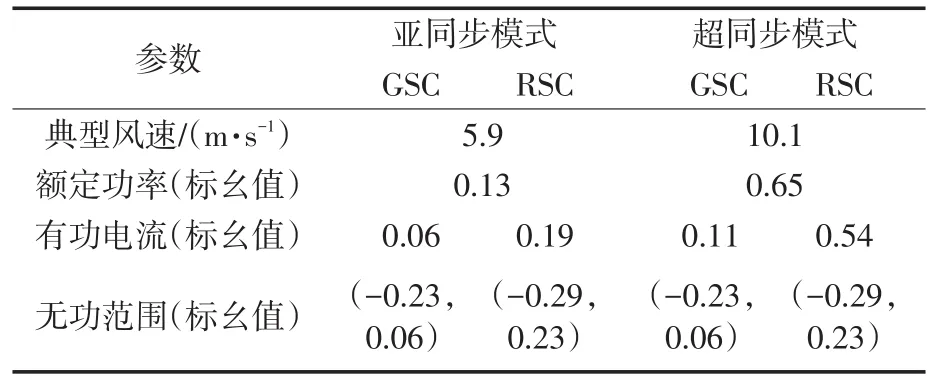
表1 典型风速下无功运行范围Tab.1 The reactive power range in typical wind speed
为了不影响并网功率因数,无功环流范围根据表1可选择为较小的GSC的范围,即(−0.23,0.06)。
图6所示为以GSC无功环流范围作为水平轴,额外的无功注入影响到电流幅值和相角φui作为垂直轴的示意图。从图6中可以看出,不论是何种工作模式,GSC侧最小电流幅值出现在无功注入为零的时候,而RSC侧最小电流幅值出现在最大容性无功注入时。从图6中还可以看出,对于相角特性,在注入无功后GSC侧单位功率因数相角明显地变为超前或滞后相角,而RSC侧则相角变化很小。
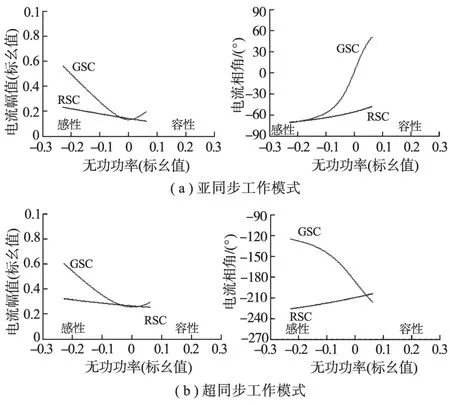
图6 典型风速下变流器电流特性Fig.6 Current characteristic of the converter in typical wind speed
3 基于无功环流的热负荷优化控制策略
如前所述,不同的无功环流将导致不同电流运行特征,进一步将对变流器中功率器件的热负荷产生影响。
3.1 正常工况下的功率器件热负荷分布
功率半导体器件IGBT和二极管的损耗可分为导通损耗和开关损耗这2类。根据相关文献,导通损耗和开关损耗都是和流过功率器件的电流相关的,可以用分段线性函数拟合建模,并结合数据手册提供的参数进行仿真计算[20]。而变流器功率器件的热传导模型可采用经典的Cauer模型,即4级RC网络模型,具体的参数也可以从器件手册上获取[20]。
图7所示为正常工况下,即没有无功注入时,风速、功率器件IGBT和二极管结温之间的关系。图7中所示风速等于8.4 m/s是模式切换点风速,可以看出,当风速超过模式切换点风速后,功率流方向逆转,在RSC侧,亚同步模式时IGBT功率损耗大于二极管,逆转后二极管损耗大于IGBT,热应力更大,而GSC则刚好相反,逆转后IGBT热应力更大。此外,还可以看出,在整个风速带范围内RSC侧的功率器件结温波动和平均值均高于GSC侧,热应力更大,这将导致变流器两侧功率器件寿命周期的失衡。
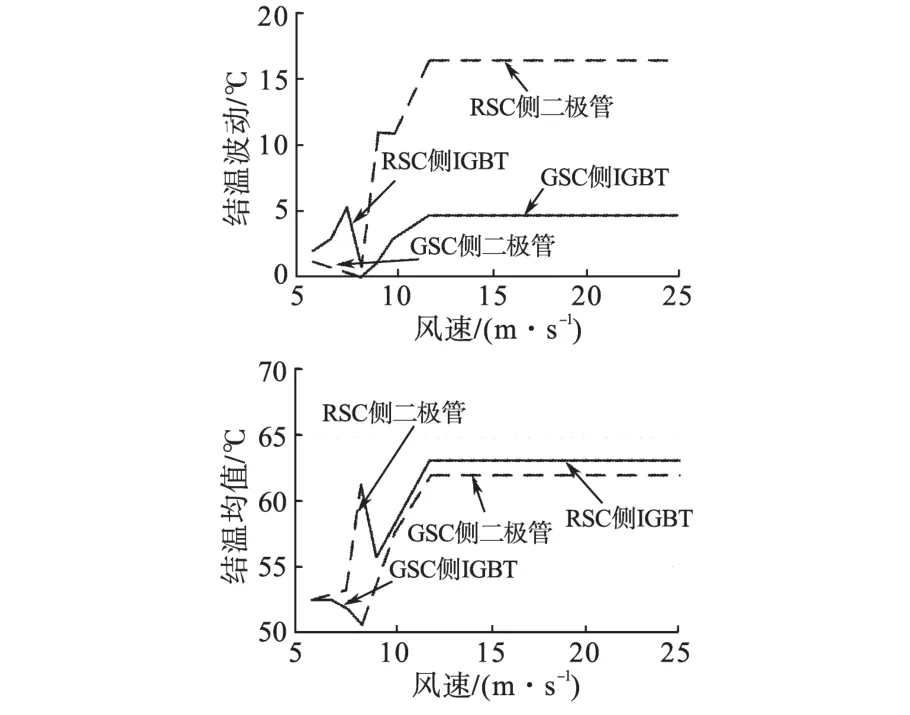
图7 风速变化时功率器件的热负荷分布Fig.7 Thermal profile of power device in different wind speeds
3.2 注入无功后的功率器件热负荷分布
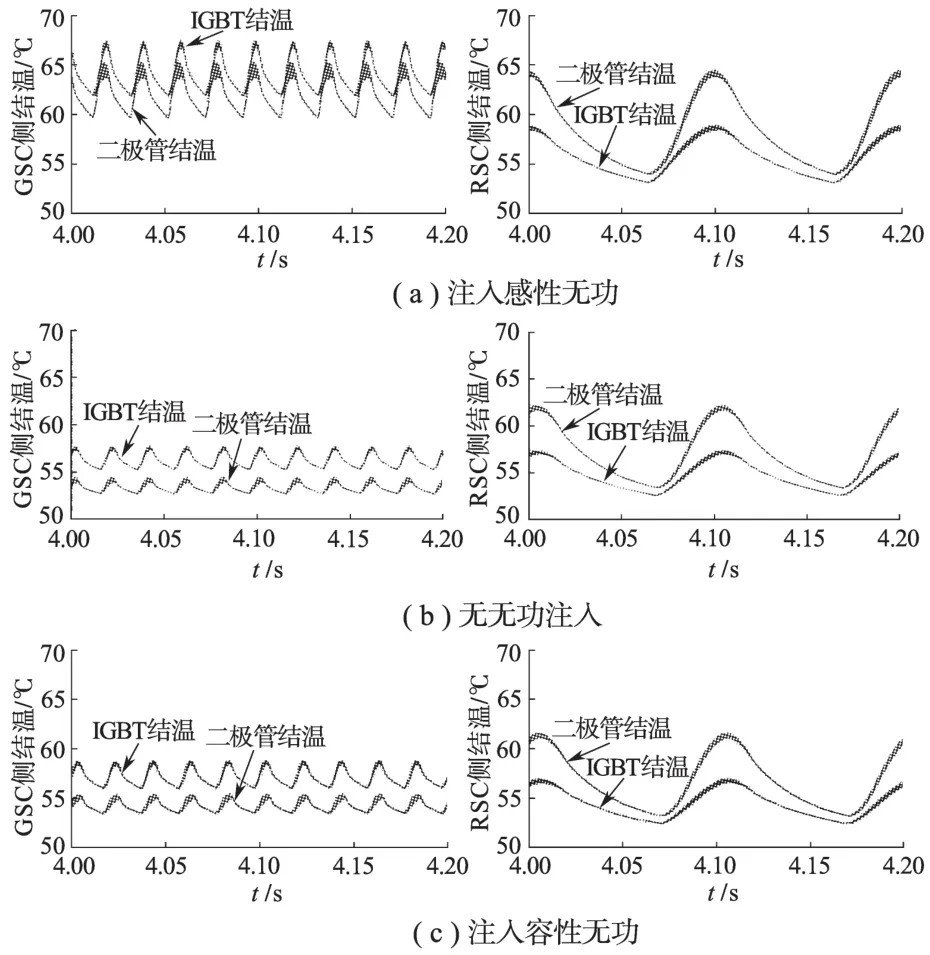
图8 超同步运行时的功率器件热负荷分布Fig.8 Thermal distribution of the power devices at supersynchronous mode
根据表1中计算的DFIG系统允许无功功率范围,可以分析计算出注入感性无功、容性无功和不注入无功时的功率器件热负荷分布。图8所示为风速10.1 m/s时,即超同步工作模式下,在注入感性无功、容性无功和不注入无功时的GSC和RSC侧的IGBT和二极管结温曲线。可以看出,对于GSC侧而言,在没有无功注入时,其功率器件结温波动和最大平均结温都最小,这也是和图6b中电流特性是一致的。还可以看出,对于RSC侧,当注入最大允许容性无功时,其功率器件结温波动和最大平均结温都达到最小,但可以注意到,注入容性无功与没有无功注入和注入感性无功时的结温特性差别不大,这是因为变流器容性无功运行边界较小,感性无功和有功功率占主导地位。
图9所示为风速5.9 m/s时亚同步模式下变流器内功率器件的热负荷分布柱状图,从中可以得到和图8相似的结论,同时从图8和图9还可以看出来,对于GSC侧,注入容性或感性无功,可以显著改变结温波动,而对于RSC侧,额外的容性无功功率注入可以一定程度降低功率热应力。

图9 亚同步运行时的功率器件热负荷分布Fig.9 Thermal distribution of the power devices at subsynchronous mode
3.3 热负荷优化控制器设计
根据上述分析,注入无功功率将显著影响变流器内功率器件的热负荷分布,基于该原理,可以设计出基于无功环流的变流器热负荷优化控制器,结合经典dq电流闭环控制,可得到热负荷优化控制器框图如图10所示。首先正常由风机模型和输入风速vw计算得到GSC和RSC的有功电流参考ird和igd,然后将参考结温Tjref代入到热传导模型计算出功率器件损耗,之后由损耗计算模型计算除去有功功率损耗后得到无功损耗所需的无功环流igq,再将igq和取反得到的irq分别送至GSC侧和RSC侧电流控制器,最后由电流控制器生成PWM控制脉冲给功率器件。控制器实现的控制目标是风速变化时,功率器件结温变化趋于平稳。

图10 变流器热负荷优化控制器框图Fig.10 Diagram of thermal behavior optimal controller for converter
4 仿真验证
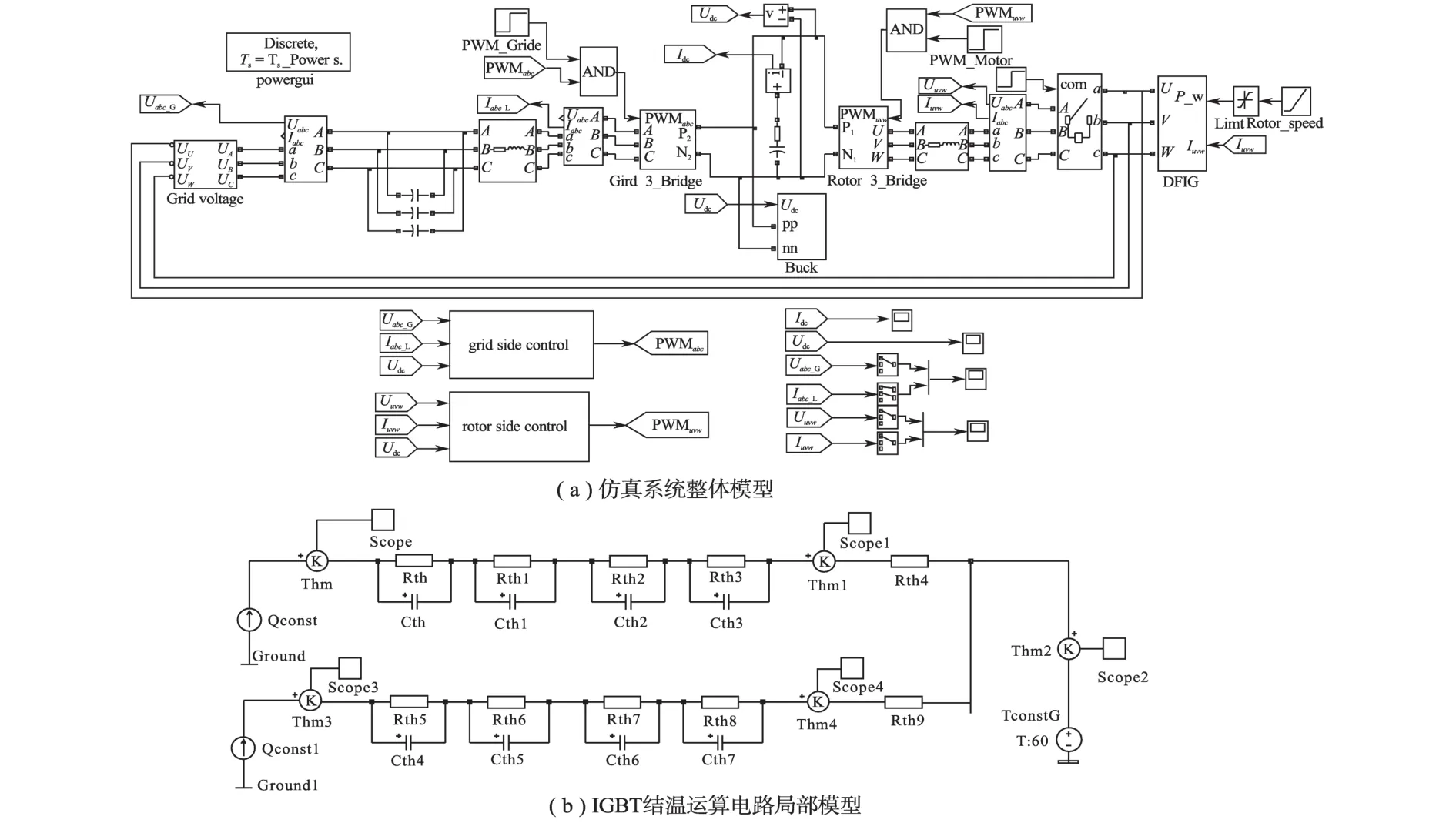
图11 风电机组的仿真模型Fig.11 Simulation model of the wind power
为验证变流器热负荷优化控制策略的性能,基于Matlab/Plecs的仿真平台搭建了DFIG风电机组的仿真模型(见图11),并进行了仿真计算,其中Matlab/Simulink中实现了电路模型,热模型最小结温也出现在同步工作点附近,而最大结温出现在风速最大的时候,GSC侧的最大结温波形达到11℃,由于没有无功注入,igq持续为0。从图12b中可以看出,新型控制下,通过注入合适的无功环流,反应在igq不再持续为0,而是随着控制律变化,GSC侧IGBT和二极管的最大结温波动只有7℃,和图12a中的11℃相比下降了4℃。因此,仿真结果验证了基于无功环流的热负荷优化控制在风速动态时能够有效降低变流器内功率器件的结温波动,从而降低器件的失效率,提高设备的可靠性。从图12中还可以注意到RSC侧的功率器件结温波形在不同控制下的变化很小,这也验证了前述分析,RSC侧由于最大允许容性无功边界小,而不注入无功和注入感性无功时的结温特性差别小,从而新型控制方案对其影响不大。则直接在Plecs中方便的调用,而模型参数与前面DFIG风电机组参数一致,仿真试验验证采用对比的方式进行。
如图12所示为传统无无功注入的控制策略和新型含无功环流的控制策略下风速动态时风电变流器内功率器件的热负荷分布计算结果。风速首先从10 m/s下降至8 m/s,然后增加至16 m/s,最后以对称的规律回到10 m/s,变化过程持续8 s,其中同步工作点风速为8.4 m/s。图12a中显示了有功功率参考趋于0在同步工作点,即igd趋于0,同时可以看出功率器件IGBT和二极管的

图12 风速动态时新型控制下的仿真结果Fig.12 Simulation results of the new control with wind dynamics
5 结论
本文主要对基于无功环流的大容量风电变流器热负荷优化控制策略进行了研究。首先分析了DFIG风电机组变流器GSC侧和RSC侧的无功功率运行边界,然后计算了注入无功环流后功率器件的热负荷分布,之后设计了热负荷优化控制器,最后基于Matlab仿真平台对控制策略进行了对比仿真验证。主要结论为:
1)双馈风电机组变流器的感性无功边界大于容性无功运行边界,而注入无功环流后,对GSC侧的功率器件结温影响大于RSC侧;
2)通过新型的变流器热负荷优化控制,GSC侧功率器件的结温波动显著减小,从而可提高机组的可靠性。
[1]陈亚爱,刘劲东,周京华,等.风力发电系统的低电压穿越技术综述[J].电气传动,2013,43(11):3-10.
[2]Chen Z,Guerrero M J,Blaabjerg F.A Review of The State of the Art of Power Electronics for Wind Turbines[J].IEEE Transactions on Power Electronics,2009,5(8):1859-1875.
[3]林鹤云,郭玉敬,孙蓓蓓,等.海上风电的若干关键技术综述[J].东南大学学报,2013,41(4):882-888.
[4]王君瑞.双馈风力发电机滑模变结构直接功率控制[J].电气传动,2014,44(5):44-47.
[5]程启明,郭凯,程尹曼,等.电网电压不平衡时DFIG网侧变流器新型双环控制策略[J].电机与控制应用,2015,42(12):35-42.
[6]陈显彪.一种双馈电机转子电流定向的矢量控制方法[J].电机与控制应用,2012,39(3):19-21.
[7]周俊杰,周洪伟,马超群,等.双馈异步发电机同步速下变流器运行状态研究[J].电气传动,2015,45(4):44-47.
[8]Kaigui X,Zefu J,Wenyuan L.Effect of Wind Speed on Wind Turbine Power Converter Reliability[J].IEEE Transactions on Energy Conversion,2012,27(1):96-104.
[9]Song Y,Wang B.Survey on Reliability of Power Electronic Systems[J].IEEE Transactions on Power Electronics,2013,28(1):591-604.
[10]Busca C,Teodorescu R,Blaabjerg F,et al.An Overview of The Reliability Prediction Related Aspects of High Power IGBTs in Wind Power Applications[J].Microelectronic Reliability,2011,51(9):1903-1907.
[11]Bryant A,Parker-Allotey N,Hamilton D,et al.A Fast Loss and Temperature Simulation Method for Power Converters,Part I:Electrothermal Modeling and Validation[J].IEEE Transactions on Power Electronics,2012,27(1):248-257.
[12]Lu B,Sharma S.A Literature Review of IGBT Fault Diagnostic and Protection Methods for Power Inverters[J].IEEE Transactions on Industry Applications,2009,45(5):1770-1777.
[13]Senturk S O,Helle L,Munk-Nielsen S,et al.Power Capability Investigation Based on Electrothermal Models of Press-pack IGBT Three-level NPC and ANPC VSCs for Multi-MW Wind Turbines[J].IEEE Transactions on Power Electronics,2012,27(7):3195-3206.
[14]Avenas Y,Dupont L,Khatir Z.Temperature Measurement of Power Semiconductor Devices by Thermo-sensitive Electrical Parameters——A Review[J].IEEE Transactions on Power Electronics,2012,27(6):3081-3092.
[15]李辉,季海婷,秦星,等.考虑运行功率变化影响的风电变流器可靠性评估[J].电力自动化设备,2013,5(35):1-8.
[16]黄伟煌,胡书举,许洪华.中点钳位型中压三电平风电变流器的损耗分析[J].电力系统自动化,2014,38(15):65-70.
[17]Jung J,Hofmann W.Investigation of Thermal Stress in Rotor of Doubly-fed Induction Generator at Synchronous Operating Point[C]//Electric Machines&Drives Conference,2011(4):896-901.
[18]Musallam M,Johnson M C.Impact of Different Control Schemes on the Lifetime Consumption of Power Electronic Modules for Variable Speed Wind Turbines[C]//European Conference on Power Electronics and Applications,2011:1-9.
[19]Lixiang W,McGuire J,Lukaszewski A R.Analysis of PWM Frequency Control to Improve the Lifetime of PWM Inverter[J].IEEE Transactions on Industry Applications,2011,47(2):922-929.
[20]Blasko V,Lukaszewski R,Sladky R.On Line Thermal Model and Thermal Management Strategy of a Three Phase Voltage Source Inverter[C]//Indastry Applications Conference,2002,2:1423-1431.
[21]Wang X,Castellazzi A,Zanchetta P.Regulated Cooling for Reduced Thermal Cycling of Power Devices[C]//Electronics and Motion Control Conference,2012,1:283-244.
Thermal Behavior Optimal Control for Wind Power Converter with Reactive Power Circulation
WAN Shengqian
(School of Electrical and Electronic Engineering,Ezhou Polytechnic,Ezhou 436000,Hubei,China)
The design service life of the large capacity of wind power converter determines its reliability which is very important.The junction temperature of the power semiconductor devices in converters will fluctuate when the power point of the converter transforms with the change of the wind speed,and this will increase the failure rate of the device,which affects the reliability of the converter.To solve it,a thermal behavior optimal control strategy for wind power converter with reactive power circulation was proposed.At first,aiming at the doubly fed induction generators wind turbines,the reactive power circulation operation boundary ranges at both the rotor side and grid side of the converter were calculated,then the influences of the current and the thermal stresses in power semiconductor devices by reactive power circulation were analyzed.Therefore,the optimal controller which add extra reactive power inject to the converter to maintain the power device thermal stability when wind speed changed was designed.Finally,the simulation model which was based on Matlab/Pecs platform was established,and some calculations were done to compare the new method and the conventional one.The results show that the new control method makes the maximum junction temperature fluctuation of the power device in converter is 4 degrees lower than the traditional method with the same change of the wind speed,and the effectiveness of the new controller is verified.
wind power converter;doubly fed induction generator(DFIG);reactive power;thermal cycling;junction temperature
TM46
A
10.19457/j.1001-2095.20171014
湖北省自然科学基金面上项目(2016CFB516)
万胜前(1973-),女,硕士,副教授,Email:507394026@qq.com
2016-10-27
修改稿日期:2017-01-05
