基于潜在地理—社会关系感知的兴趣点推荐研究
2017-11-01宋启祥李玉林戚溪溪
崔 琳,宋启祥,李玉林,戚溪溪
宿州学院信息工程学院,宿州,234000
基于潜在地理—社会关系感知的兴趣点推荐研究
崔 琳,宋启祥,李玉林,戚溪溪
宿州学院信息工程学院,宿州,234000
针对已有的兴趣点推荐模型大都采用无地理空间限制的显式社会关系和隐式社会关系进行兴趣点推荐,而基于地理空间限制的显式社会关系和隐式社会关系对兴趣点推荐结果有着极为重要的影响。为此,提出了一种新型的基于潜在地理—社会关系挖掘的兴趣点推荐模型。使用核密度估计方法对用户签到行为可达的地理影响区域进行个性化分析,然后使用所提出的两跳随机游走算法挖掘用户之间的显式社会关系和隐式社会关系,把用户可达地理区域内的显式社会关系和隐式社会关系作为一个正则项融合到传统的矩阵分解模型中。两个真实数据集上的实验结果显示所提出的潜在地理—社会关系挖掘的兴趣点推荐模型优于文中所选择的其他4个兴趣点推荐对比方法。
基于位置的社会网络;兴趣点推荐;地理-社会关系;显式社会关系;隐式社会关系
随着移动设备、无线通讯和位置获取技术的迅速发展,基于位置的社会网络(Location-based social networks,LBSN)Foursquare、Gowalla、Facebook places和豆瓣网等已吸引了成千上万用户的注意[1-3]。在这些基于位置的社会网络下,用户可以分享他们访问某一具体位置的经验,并把自己认为不错的场所,如饭店、商店和博物馆等推荐给其他用户,这就是兴趣点推荐。当前,有许多关于兴趣点推荐研究的工作。其中,一些研究显示人们总是探索他们之前访问过兴趣点附近的位置[4-5],因此被用户访问过的兴趣点常常呈现出空间聚类的特征。一些研究工作聚焦于使用LBSN中的用户关系来改善推荐性能,此工作把所有存在社会链接关系的相似度作为正则项融合到推荐系统中来约束矩阵分解;然而,在推荐任务中,只依赖于用户之间直接存在的显式链接社会关系是不太有效的[6]。
在基于位置的社会网络下,挖掘某一特定的地理区域下用户之间的显式—隐式社会关系非常重要。例如,对于用户Linda,假设存在两种类型的用户和Linda有地理—社会相关性,一种类型的用户是在Linda可达的地理空间下和Linda有直接联系的用户,被定义为与Linda存在显式社会关系的用户;另一种类型的用户是在Linda可达的地理空间下,Linda朋友的朋友,与Linda之间通过Linda的朋友间接和Linda存在关系,这种关系在本文中被定义为用户之间的隐式社会关系。在Linda可以到达的区域,借助于显式—隐式用户关系,能够为Linda推荐Linda未签到的,但又是Linda有可能感兴趣的兴趣点。
受上边例子所启发,本文提出一种基于潜在地理—社会关系感知的兴趣点推荐模型(Potential Geo-Social Relationship Awareness for Point of Interest Recommendation,PGSR-PR)。在地理—社会关系挖掘阶段,用户间的显式—隐式地理-社会关系使用核密度估计方法和两跳随机游走算法被识别出来。然后,把识别出的显式—隐式地理—社会关系作为一个正则项融合到矩阵分解中。最后,使用改进的矩阵分解模型实现把前N个兴趣点的推荐列表(top-N)推荐给用户。这是第一个聚焦于某一地理区域下的显式—隐式用户关系的兴趣点推荐模型。为了验证PGSR-PR模型的有效性,与其他4种基线方法在Foursquare和Gowalla数据集上作了实验结果比较与分析,结果显示所提出的PGSR-PR模型在精确率(P@N)、召回率(R@N)和归一化折扣累计增益(NDCG)指标上优于其他4种基线方法。
1 相关工作
以下介绍与本研究相关的三项研究工作,即传统推荐方法、矩阵分解技术、基于地理空间关系和社会关系的兴趣点推荐方法。
1.1 传统推荐方法
传统推荐方法分为基于内容的方法和协同过滤方法两类[7]。基于内容的推荐方法主要依据推荐项目和用户画像内容信息的相关性,为用户推荐相关的项目[8],但是不能灵活地结合与用户相关的各种各样的信息,故很少被用于兴趣点推荐。协同过滤率方法主要分为基于记忆的方法和基于模型的方法两类[9]。例如,Ye等人采用基于记忆的方法执行兴趣点推荐,然而,基于记忆的推荐方法通常面临冷启动和数据稀疏性等问题[10]。基于模型的推荐方法已被广泛应用于兴趣点推荐[11],这种方法把原始的评分矩阵拟合为一个模型,通过概率分布或者低维矩阵减少模型的维度和稀疏性,然后被应用于预测未评价项目的分数。在基于不同模型的方法中,矩阵分解是一种最被常用的方法,由于其可扩展性和更为精确的优势,已引起许多关注。
1.2 矩阵分解技术
矩阵分解已被成功地用于各种各样的推荐系统,它假设用户和项目(兴趣点、电影和产品等)能够被建模成潜在表示集合,在一起确定未评分项目的爱好[12]。许多矩阵分解模型已被用于兴趣点推荐领域,例如,Zhao等人通过使用用户、地点和时间的异构关系,提出一种贝叶斯概率张量分解模型去抽取推荐的社会维度[13];Hu等人通过考虑项目的内在特征和它的地理邻居的外在特征,开发了一种基于矩阵分解的潜在因子模型用于地理评分预测,与其他方法相比较,此模型能获得更低的预测误差[14]。
1.3 基于地理空间关系和社会关系的兴趣点推荐方法
在基于位置的社会网络下,用户的朋友比非朋友能分享更多的用户自身感兴趣的信息,一些兴趣点推荐方法通过考虑社会关系来改善推荐的质量。Berjani等人在基于位置的社会网络下提出基于正则矩阵分解的兴趣点推荐方法[15]。Ye等人基于朋友共同访问的签到数,提出了基于朋友的协同过滤方法用于兴趣点推荐,基于朋友间的社会链接关系和他们签到活动的相似度,推导了两个朋友间的社会影响权重[16]。Li等人开发了一个新的社会朋友概率矩阵分解模型,在社会朋友空间,用户爱好被假设通过社会网络传播,重复访问他的朋友访问过的历史兴趣点[1]。
最新研究显示位置的地理临近性大大影响用户的签到行为。Liu等人观察发现用户总是访问离家或者办公室近的位置,也比较感兴趣探索他们访问过的位置就近的地方。他们假设被同一个用户访问的两个位置之间的地理距离遵循幂律分布[17]。Cheng等人论述用户总是访问中心周围(即最经常访问的兴趣点)的位置,并假设签到位置在每个中心周围遵循高斯分布[18]。Lian等人提出一个包含地理因素的加权正则化矩阵分解模型来提升兴趣点的推荐性能[5]。
观察以上研究工作,发现用户的签到行为明显受用户的爱好、用户间的社会关系和所处的地理空间影响。已有许多兴趣点推荐研究考虑用户的爱好、他们的社会关系和地理空间。然而,仍然没有同时考虑在用户可达的某一区域内,有关用户之间显式—隐式地理—社会关系对兴趣点推荐的影响研究。因此,本文聚焦已有研究工作所忽略的在用户可达的某一区域内相关用户之间显式—隐式地理—社会关系对兴趣点推荐的影响,提出PGSR-PR模型。
2 研究准备
基于位置的社会网络包含丰富的信息,假设u={u1,u2,…,um}⊂U,p={p1,p2,…,pn}⊂P分别是用户的子集和兴趣点的子集。所谓兴趣点(Point of Interest),就是指在基于位置的社会网络下,可以被识别出的具体事件和地点。如果用户ui已在兴趣点pj签到,则规定rij≠0,否则rij=0。给定来自基于位置社会网络下的社会链接,构建一个社会链接关系矩阵SU×U,如果在不同的用户ui∈U与uk∈U之间存在链接,Sui,uk=1,否则Sui,uk=0。兴趣点推荐问题转化为在兴趣点P中根据用户的签到行为为用户u推荐新的未访问过的兴趣点。为便于阅读,表1描述了本文所用到的一些概念。

表1 相关概念列表
3 基于潜在地理—社会关系感知的兴趣点推荐方法
以下详细介绍所提出的基于核密度估计和两跳随机游走算法的潜在地理—社会关系感知兴趣点推荐方法,把基于核密度估计和两跳随机游走算法的潜在地理—社会关系作为正则项融合到矩阵分解推荐方法中,使用随机梯度下降算法(Stochastic Gradient Descent,SGD)学习相应的模型参数。
3.1 挖掘潜在地理—社会关系感知信息
地理位置的个性化影响在个性化用户签到行为中扮演着重要的角色,本文使用核密度估计方法建模被用户访问的两个位置之间的距离的个性化分布。分析用户签到的地理位置,发现用户在连续时间内总是访问上次签到兴趣点就近的地方,并且访问一个位置的意愿随着离当前位置距离的增加而减少。使用核密度估计方法,首先计算位置Li和位置lo之间的距离,计算方法如下:
dio=distance(Li,lo), ∀li∈Li
(1)
在距离d∈D上的核密度估计f,计算如下:
(2)
其中,D是一个特定用户的距离样本,来自于未知密度f的分布,K(·)是核函数,h是路径距离衰减阈值,叫作带宽。n是兴趣点的个数,兴趣点和其他位置s的距离小于或者等于h。使用正则化核,表示如下:
(3)
最优化带宽表示如下:
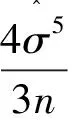
(4)
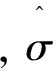
基于核密度的距离度量后,基于公式(5)来推断用户ui访问新位置lo的概率,给定访问位置Li={l1,l2,…,ln}的集合。最后,用户ui访问新位置lo的概率,采用公式(5)表述的概率平均值获得:
(5)
另外,本文采用所提出的两跳随机游走算法来计算用户之间显式—隐式链接关系相似度。两跳随机游走模型是指从一个给定的用户节点游走到一个任何他的邻居节点的过程。用户ui和用户uj之间的显式—隐式关系被定义为从用户ui到用户uj之间随机游走的平均步数:
(6)
其中,score(e)表示存在用户节点ui和用户uj之间的未知链接e的评分,这个值也被看作是用户节点ui和用户uj之间的相关度。paths(i,j)表示节点ui和用户uj之间的所有路径的集合,edges(p)是包含在路径p中的所有边的集合,p(e′)是在随机游走时选择边e′的概率。p(e′)值的中心思想是,边e′的权重越大,p(e′)的值也越大。边e′起始节点的邻接边集合的权重之和越大,p(e′)的值就越小,公式定义如下:
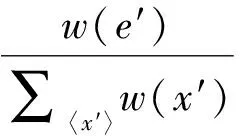
(7)
其中,w(e′)表示边e′的权重,x′表示边e′的初始边,〈x′〉表示边x′的邻接边集合。
在由用户集合构成的无向图中,因为用户集合的规模非常大,图也很复杂,计算两个用户节点之间所有路径集合的计算成本也非常高。因此,在执行随机游走操作时,每次游走只在边数小于或者等于3的路径内进行,也就是本文定义的两跳(Two-hop)。
通过推断目标用户的显式—隐式朋友在兴趣点上的爱好和他们的个性化移动模式(使用核密度估计计算),融合这两个因素来推断目标用户ui在一个兴趣点o签到的概率。在用户ui可达区域内,用户ui和其潜在朋友集合的相似度采用公式(8)进行计算:
wik=p(loLi)·p(e′)
(8)
公式(8)融合了用户爱好、社会影响和两个用户居住距离的地理影响到基于位置的兴趣点推荐过程中。
3.2 传统的矩阵分解模型
传统的矩阵分解推荐模型假设存在潜在因子影响用户的签到行为或者评分行为,在用户—项目评分矩阵中执行低秩矩阵分解。让Ui∈Rm×k表示用户ui的用户爱好矩阵,Pj∈Rn×k表示兴趣点pj的兴趣点特征矩阵,其中,K是潜在因子个数,并假设K≪(m,n)。传统的基于矩阵分解的推荐模型的主要思想可以通过如下公式表示:
(9)

(10)
3.3 基于潜在地理—社会关系感知的兴趣点推荐模型
使用传统的矩阵分解模型作为基础,嵌入潜在地理—社会关系感知因素,引入本文所提出的PGSR-PR模型捕获潜在地理—社会关系感知的兴趣点推荐。在传统低秩矩阵分解模型基础上,PGSR-PR模型定义的目标函数如下:
(13)
其中,参数β旨在平衡潜在地理—社会关系对兴趣点推荐影响的效果,把它作为一个正则化项来约束矩阵分解,以获得更高的推荐准确率。
3.4 基于潜在地理—社会关系感知的兴趣点推荐模型的优化
本文使用随机梯度下降算法(Stochastic Gradient Descent,SGD)来优化目标函数。随机梯度下降算法随机扫描所有的训练数据并针对每一个用户—兴趣点元素,沿着目标函数梯度下降的方向更新参数。模型优化更新采用如下公式执行:
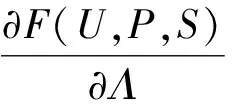
(14)
其中,ξ是学习率,Λ表示所有被包含的参数,∂F(·)对应公式(13)中的目标函数。为了获得公式(14)中Ui和Pj的梯度,目标函数的最小化可以通过执行随机梯度算法来进行计算,分别对参数Ui和Pj引入梯度计算和更新。
与用户Ui有关的梯度采用公式(15)进行计算:
(15)
因此,Ui被更新为:
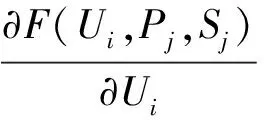
(16)
与Pj有关的梯度采用公式(17)进行计算:
(17)
Pj被更新为:
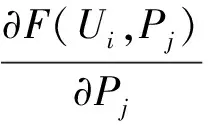
(18)
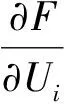

表2 基于潜在地理—社会关系感知的兴趣点推荐模型算法
4 实验结果和分析
4.1 实验数据集
采用从Foursquare和Gowalla网站抓取的数据集。第一个Foursquare数据集来自Gao等人所挖掘的数据集[2],第二个实验数据集来自Zhao等人所挖掘的数据集[19]。这两个数据集中的每一条签到记录包含用户ID、位置ID以及用户在某一位置的签到频率、用户画像、用户友谊关系、位置画像和用户的签到历史。在本实验中,前期数据预处理时,过滤掉了签到次数小于、等于10的用户和少于10个用户签到的兴趣点个数。
4.2 实验设置与实验比较方法
在实验设置中,设定学习率ξ=0.001,潜在因子K从{10,20,30,40,50,60,70,80}中多次进行选择,参数λ和β从{0,0.01,0.05,0.1,0.5,1}中进行选择验证,观察发现当K=40,λ=β=0.05时所提出的模型性能最优。为了体现实验比较的公正性,同样的参数设置用于其他4个比较方法中。另外,每个数据集被划分为训练集和测试集,签到数据的80%用作训练集,剩余的20%当作测试集。
为了评价所提出PGSR-PR模型的性能好坏,把PGSR-PR模型与BasicMF模型[12]、Biased MF模型[14]、PMF模型[20]和GeoCF模型[21]进行了实验结果比较与分析,有关这4个基线比较方法的介绍,详见相关参考文献。
4.3 评价指标
本研究的主要任务就是为目标用户预测一个精确的兴趣点推荐列表,为了评价在真实情景中兴趣点推荐的有效性,采用如下三个评价指标来衡量PGSR-PR模型的有效性,即准确率P@N、召回率R@N和排序度量指标(Normalized discounted cumulative gain)NDCG@N。三种指标的具体定义如下:

(19)

(20)
其中,#TestSetHits是用户在测试集上已签到的兴趣点集合,P@N主要用来检查兴趣点推荐排序的准确率问题,R@N主要用来检查兴趣点推荐排序的召回率问题。使用NDCG@N来衡量基于推荐实体评分相关性的推荐系统性能,NDCG@N值的范围从0.0到1.0变动,值为1.0表示排序列表中实体的最理想排序。NDCG被定义如下:
(21)
N是能被推荐的实体的最大数,如果在位置j的项是一个被推荐的项时,rj是1,否则rj=0。
4.4 在评价指标P@N和R@N上的实验结果比较与分析
在Foursquare数据集和Gowalla数据集上,把PGSR-PR模型与已有的4种方法在评价指标P@N和R@N上进行比较分析。首先分析每种方法的P@N和R@N随着推荐列表长度Top-N如何变化,N的值分别设为5、10、15和20。在Foursquare数据集上,P@N和R@N比较结果如图1所示。从图1可以看出,PGSR-PR模型在不同的N取值上一直优于其他4种基线方法。由于PMF方法优于BasicMF方法和Biased MF方法,GeoCF方法又优于PMF方法。所以本文提出的PGSR-PR模型在3个评价指标上与GeoCF模型相比较,性能又有进一步改善。在Gowalla数据集上,P@N和R@N的比较结果如图2所示,实验比较结果与在Foursquare数据集对应的比较结果类似,PGSR-PR模型在P@N和R@N指标比较上,依然显示出最优性能。
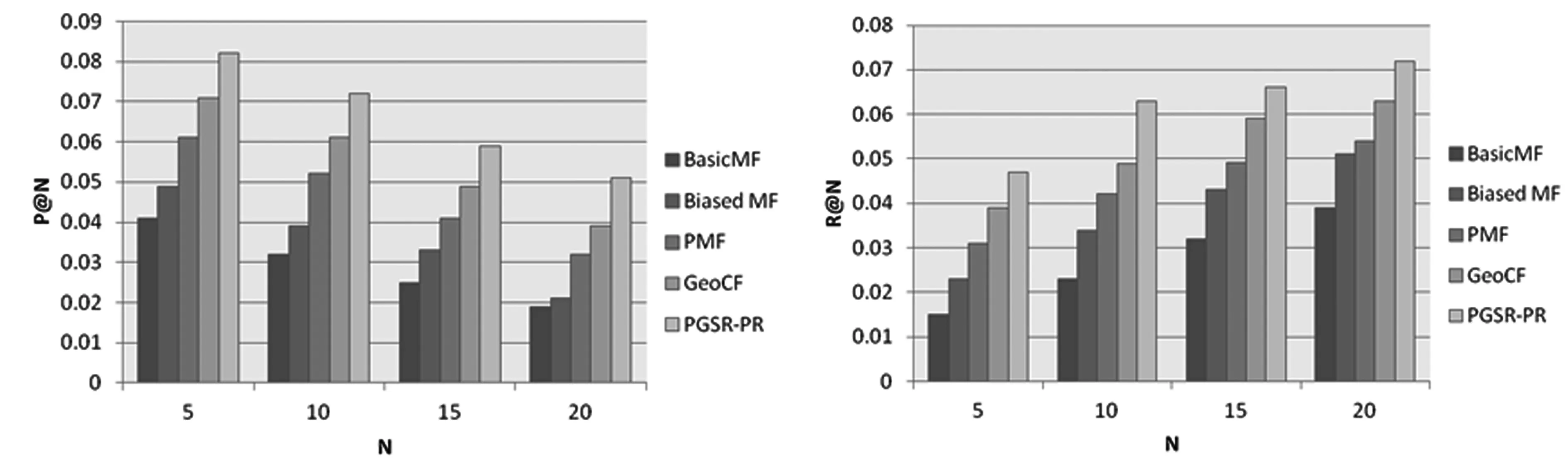
图1 在Foursquare数据集上5模型的Top-N推荐性能比较

图2 在Gowalla数据集上5种模型的Top-N推荐性能比较
4.5 在评价指标P@10、R@10和NDCG@10上的实验结果比较与分析
为了更好地验证实验效果,表3呈现了在Foursquare数据集上,当N=10时,PGSR-PR模型与其他4种方法中效果最好的Geo-CF模型相比,各评价指标的相对改善效果。从实验结果可以观察到,PGSR-PR模型相对于Geo-CF模型有明显的改善,P@10的值有18.03%的改善,R@10的值有29.17%的改善,NDCG@N值有13.04%的改善。表4呈现了在Gowalla数据集上当N=10时,PGSR-PR模型和Geo-CF模型相比,各评价指标的相对改善效果。从实验结果可以观察到,PGSR-PR模型相对于Geo-CF模型有明显的改善,P@10的值有14.04%的改善,R@10的值有29.79%的改善,NDCG@N值有12.70%的改善。总之,本文所提出的方法优于其他基线方法,显示了所提出的PGSR-PR模型的优越性。
表3PGSR-PR模型与GeoCF在Foursquare数据集上的比较结果(N=10)
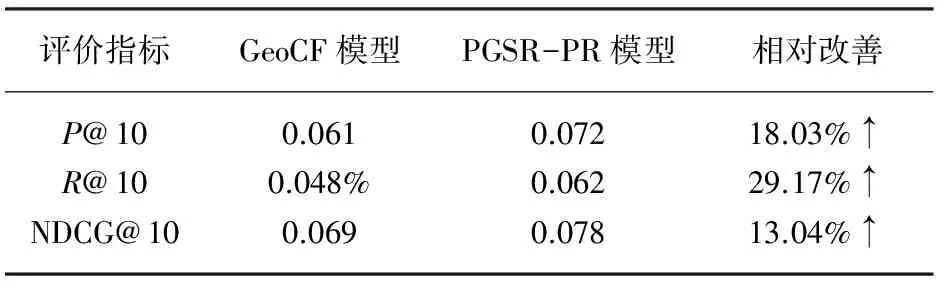
评价指标GeoCF模型PGSR-PR模型相对改善P@100.0610.07218.03%↑R@100.048%0.06229.17%↑NDCG@100.0690.07813.04%↑
表4PGSR-PR模型与GeoCFO模型在Gowalla数据集上的比较结果(N=10)
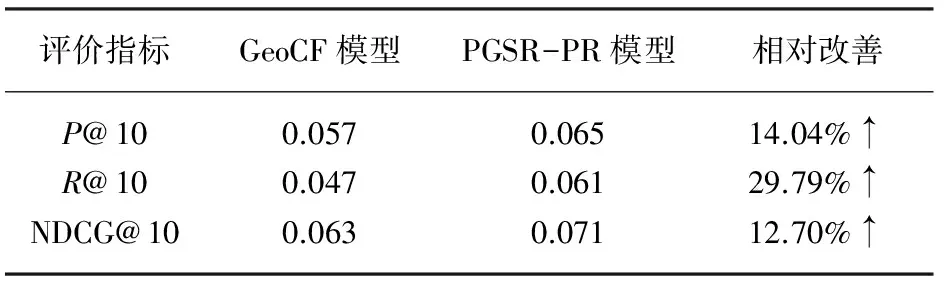
评价指标GeoCF模型PGSR-PR模型相对改善P@100.0570.06514.04%↑R@100.0470.06129.79%↑NDCG@100.0630.07112.70%↑
5 结束语
本文提出一种基于核密度估计和两跳随机游走算法的潜在地理—社会关系感知的兴趣点推荐模型。所提出的兴趣点推荐模型考虑了在用户可达区域内,用户的兴趣相似度和用户的显式—隐式链接关系对兴趣点推荐的影响。实验结果验证了所提出的PGSR-PR模型优于其他4种被广泛使用的兴趣点推荐方法。这是因为所提出的PGSR-PR模型考虑了在用户可达范围内用户之间的显式—隐式地理—社会关系相似度。在下一步的研究工作中,有几个感兴趣的方向可以值得探索。首先,在基于位置的社会网络下,除了考虑某一特定区域用户之间的隐式链接关系外,用户之间的签到行为会随时间而发生变化,因此,下一步计划探索兴趣点推荐中的时间影响因素。其次,用户针对兴趣点的评论信息大大有利于深入挖掘用户之间的关系,分析用户在兴趣点推荐的评论将更值得研究。
[1]Li H,Hong R,Zhu S,et al.Point-of-interest recommender systems: A separate-space perspective[C]//2015 IEEE International Conference on Data Mining.Atlantic City,2015: 231-240
[2]Gao H,Tang J,Liu H.gscorr:modeling geo-social correlations for new check-ins on location-based social networks[C]//Proceedings of the 21st ACM International conference on Information and knowledge management.Maui,2012:1582-1586
[3]Tang J,Hu X,Gao H,et al.Exploiting local and global social context for recommendation[C]//Proceedings of the 23rd International Joint Conference on Artificial Intelligence.Beijing,2013:264-269
[4]Liu Y,Wei W,Sun A,et al.Exploiting geographical neighborhood characteristics for location recommendation[C]//Proceedings of the 23rd ACM International Conference on Conference on Information and Knowledge Management.Shanghai,2014:739-748
[5]Lian D,Zhao C,Xie X,et al.Geomf: joint geographical modeling and matrix factorization for point-of-interest recommendation[C]//Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining.New York,2014:831-840
[6]Zhang Q,Wu J,Yang H,et al.Global and local influence-based social recommendation[C]//Proceedings of the 25th ACM International on Conference on Information and Knowledge Management.Indianapolis,2016:1917-1920
[7]Melville P,Mooney R J,Nagarajan R.Content-boosted collaborative filtering for improved recommendations[C]//The Eighteenth National Conference on Artificial Intelligence.Edmonton,2002:187-192
[8]Cantador I,Bellogin A,Vallet D.Content-based recommendation in social tagging systems[C]//Proceedings of the fourth ACM conference on Recommender systems.Barcelona,2010:237-240
[9]Koren Y.Collaborative filtering with temporal dynamics[J].Communications of the ACM,2010,53(4): 89-97
[10]Ye M,Yin P,Lee W C.Location recommendation for location-based social networks[C]//Proceedings of the 18th ACM SIGSPATIAL International conference on advances in geographic information systems.San Jose California,2010:458-461
[11]Jiang S,Qian X,Shen J,et al.Author topic model-based collaborative filtering for personalized poi recommendations[J].IEEE Transactions on Multimedia,2015,17(6):907-918
[12]Koren Y,Bell R,Volinsky C.Matrix factorization techniques for recommender systems[J].Computer,2009,42(8):30-37
[13]Zhao Y,Nie L,Wang X,et al.Personalized recommendations of locally interesting venues to tourists via cross-region community matching[J].ACM Transactions on Intelligent Systems and Technology,2014,5(3):50
[14]Hu L,Sun A,Liu Y.Your neighbors affect your ratings:on geographical neighborhood influence to rating prediction[C]//Proceedings of the 37th International ACM SIGIR conference on Research & development in information retrieval.Gold Coast,2014:345-354
[15]Berjani B,Strufe T.A recommendation system for spots in location-based online social networks[C]//Proceedings of the 4th Workshop on Social Network Systems.New York,2011:4-5
[16]Ye M,Yin P,Lee W.Location recommendation for location-based social networks[C]//Proceedings of the 18th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems.California,2010:458-461
[17]Liu X,Liu Y,Aberer K,et al.Personalized point-of-interest recommendation by mining users’ preference transition[C]//Proceedings of the 22nd ACM International Conference on Information & Knowledge Management.San Francisco,2013:733-738
[18]Cheng C,Yang H,King I,et al.Fused matrix factorization with geographical and social influence in location-based social networks[C]//AAAI Conference on Artificial Intelligence.Ontario,2012:1-2
[19]Zhao S,King I,Lyu M R.Capturing geographical influence in poi recommendations[C]//International Conference on Neural Information Processing.Springer,2013:530-537
[20]Salakhutdinov R,Mnih A.Probabilistic matrix factorization[C]//International Conference on Neural Information Processing Systems.Kitakyushu,2007:1257-1264
[21]Ye M,Yin P,Lee W,et al.Exploiting geographical influence for collaborative point-of-interest recommendation[C]//Proceedings of the 34th International ACM SIGIR Conference on Research and Development in Information Retrieval.Beijing,2011:325-334
Point-of-interestRecommendationbasedonPotentialGeo-SocialRelationshipAwareness
CUI Lin,SONG Qixiang,LI Yulin,QI Xixi
School of Information Engineering,Suzhou University,Suzhou,234000
Under the location based social networks,the existing POI recommendation models mostly adopt the explicit social relations and implicit social relations without the limitations of geographic space.However,the explicit and implicit social relations within a limited geographical space are rarely considered for points of interest (POI) recommendation.Therefore,a new potential Geo-social POI recommendation model under a certain geographical areas is put forward.The proposed model utilizes the kernel density estimation method to analyze the geographical influence on the users behavior,the two-hop random walk algorithm is proposed to mine the explicit and implicit social influence on users,then in a reachable geographical region,the explicit and implicit social relations are regarded as a regularization term for the matrix factorization.The goal of the proposed model is to recommend new POIs for users in areas where a user can reach.Experiments on two real world datasets show that the proposed POI recommendation model outperforms other state-of-the-art four recommendation methods.
Location-based Social Network,Point of interest Recommendation,Geo-Social Relationship,Explicit Social Relationship,Implicit Social Relationship
TP301.6
A
1673-2006(2017)09-0096-07
(责任编辑刘小阳)
10.3969/j.issn.1673-2006.2017.09.023
2017-04-08
国家自然科学青年基金项目(61702355);安徽高校自然科学研究重点项目(KJ2016A768);安徽省软科学研究计划项目(1607a0202071);教育部科技发展中心“云数融合科教创新”项目(2017A10014)。
崔琳(1979-),女,安徽砀山人,硕士,副教授,研究方向:兴趣点推荐、数据挖掘与分析。
